1.4: Problemas de ejercicio

1. Calcular el campo eléctrico creado por un filamento delgado, largo y recto, cargado eléctricamente con una densidad lineal constante\(\ \lambda\), utilizando dos enfoques:
   1. directamente de la ley Coulomb, y
   2. utilizando la ley Gauss.
2. Dos filamentos delgados y rectos paralelos, separados por distancia\(\ \rho\), transportan cargas iguales y opuestas distribuidas uniformemente con densidad lineal\(\ \lambda\) — vea la figura a la derecha. Calcular la fuerza (por unidad de longitud) de la interacción de Coulomb de los cables. Comparar su dependencia\(\ \rho\) con la ley Coulomb para la fuerza
   entre dos cargas puntuales.

   

3. Una esfera de radio\(\ R\), cuyo volumen había sido cargado con una densidad constante\(\ \rho\), se divide con un hueco plano muy estrecho que pasa por su centro. Calcular la fuerza de la repulsión electrostática mutua de los dos hemisferios resultantes.
4. Un caparazón esférico delgado de radio\(\ R\), que había sido cargado con una densidad de área constante\(\ \sigma\), se divide en dos mitades iguales por un corte plano muy estrecho que pasa por el centro de la esfera. Calcular la fuerza de repulsión electrostática entre las conchas hemisféricas resultantes, y comparar el resultado con el del problema anterior.
5. Calcular la distribución del potencial electrostático creado por un filamento recto y delgado de longitud finita\(\ 2l\), cargado con una densidad lineal constante\(\ \lambda\), y explorar el resultado en los límites de distancias muy pequeñas y muy grandes del filamento.
6. Una lámina plana delgada, tal vez de forma irregular, lleva una carga eléctrica con una densidad de área constante\(\ \sigma\).
   1. Expresar el componente del campo eléctrico normal al plano, a cierta distancia del mismo, a través del ángulo sólido\(\ \Omega\) en el que la hoja es visible desde el punto de observación.
   2. Usa el resultado para calcular el campo en el centro de un cubo, con una cara cargada con una densidad constante\(\ \sigma\).
7. Se pueden crear, en una región extendida del espacio, campos electrostáticos con los componentes cartesianos proporcionales a los siguientes productos de coordenadas cartesianas\(\ \{x, y, z\}\):
   1. \(\ \{y z, x z, x y\}\),
   2. \(\ \{x y, x y, y z\}\)?
8. Se han utilizado fuentes distantes para crear diferentes campos eléctricos en dos lados de una membrana metálica ancha y delgada, con un agujero redondo de radio R en ella; vea la figura a la derecha. Además de la perturbación local creada por el agujero, los campos son uniformes:

   

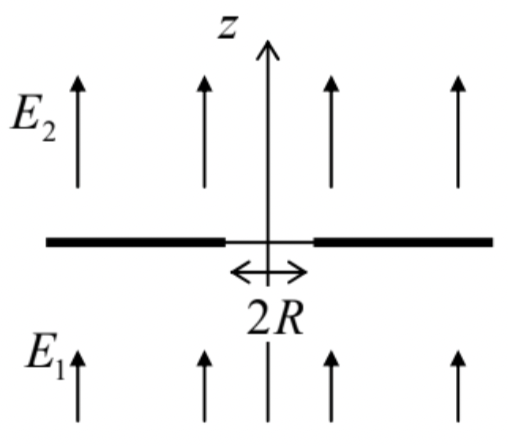
   \(\ \left.\mathbf{E}(\mathbf{r})\right|_{r>>R}=\mathbf{n}_{z} \times \begin{cases}E_{1}, & \text { at } z<0, \\ E_{2}, & \text { at } z>0 .\end{cases}\)

   Demuestre que el sistema puede servir como una lente electrostática para partículas cargadas que vuelan a lo largo del\(\ z\) eje, a distancias\(\ \rho<<R\) de él, y calcule la distancia focal\(\ f\) de la lente. Deletrea las condiciones de validez de tu resultado.

9. Ocho cargas de igual punto\(\ q\) se encuentran en las esquinas de un cubo de lado\(\ a\). Calcular todos los componentes cartesianos\(\ E_{j}\) del campo eléctrico, y sus derivadas espaciales\(\ \partial E_{j} / \partial r_{j^{\prime}}\), en el centro del cubo, donde\(\ r_{j}\) están las coordenadas cartesianas orientadas a lo largo de los lados del cubo — vea la figura a la derecha. ¿Todos tus resultados son válidos para el centro de un plano cuadrado, con cuatro cargas iguales en sus esquinas?

   

10. Mediante un cálculo directo, se encuentra el potencial eléctrico promedio de una superficie esférica de radio\(\ R\), creada por una carga puntual\(\ q\) ubicada a una\(\ r>R\) distancia del centro de la esfera. Utilice el resultado para probar el siguiente teorema del valor medio general: el potencial eléctrico en cualquier punto siempre es igual a su valor promedio en cualquier superficie esférica con el centro en ese punto, y que no contiene cargas eléctricas en su interior.
11. Dos discos similares delgados, circulares y coaxiales de radio\(\ R\), separados por distancia\(\ 2d\), se cargan uniformemente con densidades de área iguales y opuestas\(\ \pm \sigma\) — ver la figura a la derecha. Calcular y esbozar la distribución del potencial electrostático y el campo eléctrico de los discos a lo largo de su eje común.

    

12. En cierto marco de referencia, el potencial electrostático, creado por alguna distribución de carga eléctrica, es

    \(\ \phi(\mathbf{r})=C\left(\frac{1}{r}+\frac{1}{2 r_{0}}\right) \exp \left\{-\frac{r}{r_{0}}\right\},\)

    donde\(\ C\) y\(\ r_{0}\) son constantes, y\(\ r \equiv|\mathbf{r}|\) es la distancia desde el origen. Calcular la distribución de carga en el espacio.

13. Una lámina plana delgada, cortada en forma de rectángulo de tamaño\(\ a \times b\), se carga eléctricamente con una densidad de área constante\(\ \sigma\). Sin un cálculo explícito de la distribución espacial\(\ \phi(\mathbf{r})\) del potencial electrostático inducido por esta carga, encuentra la relación de sus valores en el centro y en las esquinas del rectángulo.

    Pista: Considera dividir el rectángulo en varias partes similares y usar el principio de superposición lineal.

14. Calcular la energía electrostática por unidad de área del sistema de dos planos delgados, paralelos con cargas iguales y opuestas de una densidad de área constante\(\ \sigma\), separados por distancia\(\ d\).
15. El sistema analizado en el problema anterior (dos planos delgados, paralelos, con carga opuesta) ahora se coloca en un campo eléctrico externo, uniforme, normal\(\ E_{\mathrm{ext}}=\sigma / \varepsilon_{0}\) — ver la figura a la derecha. Encuentra la fuerza (por unidad de área) que actúa en cada plano, por dos métodos:

    

    1. directamente desde la distribución del campo eléctrico, y
    2. a partir de la energía potencial del sistema.
16. Explorar la relación entre la ecuación de Laplace (42) y la condición del mínimo de la energía de campo electrostático (65).
17. Demostrar el siguiente teorema de reciprocidad de la electrostática: ²⁹ si dos distribuciones de carga espacialmente confinadas\(\ \rho_{1}(\mathbf{r})\) y\(\ \rho_{2}(\mathbf{r})\) crear distribuciones respectivas\(\ \phi_{1}(\mathbf{r})\) y\(\ \phi_{2}(\mathbf{r})\) del potencial electrostático, entonces

    \(\ \int \rho_{1}(\mathbf{r}) \phi_{2}(\mathbf{r}) d^{3} r=\int \rho_{2}(\mathbf{r}) \phi_{1}(\mathbf{r}) d^{3} r.\)

    Pista: Considera integral\(\ \int \mathbf{E}_{1} \cdot \mathbf{E}_{2} d^{3} r\).

18. Calcular la energía de interacción electrostática de dos esferas, de radios\(\ R_{1}\) y\(\ R_{2}\), cada una con una distribución de carga esféricamente simétrica, separadas por distancia\(\ d>R_{1}+R_{2}\).
19. Calcular la energía electrostática\(\ U\) de una cáscara esférica (generalmente, gruesa), con carga\(\ Q\) uniformemente distribuida a través de su volumen — ver la figura a la derecha. Analizar e interpretar la\(\ U\) dependencia del radio de la cavidad interna\(\ R_{1}\), en fijo\(\ Q\) y\(\ R_{2}\).

---

Referencia

²⁹ Este es sólo el más simple de varios teoremas de reciprocidad en el electromagnetismo — véase, por ejemplo, Sec. 6.8 abajo.