2.6: Los problemas de límites más simples

En el caso general cuando la distribución del campo eléctrico en el espacio libre entre los conductores no se puede encontrar fácilmente a partir de la ley de Gauss o de una simetría particular, el mejor enfoque es tratar de resolver la ecuación diferencial de Laplace (1.42), con condiciones de límite (1b):

Problema típico de límites

\[\ \nabla^{2} \phi=0,\left.\quad \phi\right|_{S_{k}}=\phi_{k},\tag{2.35}\]

donde\(\ S_{k}\) está la superficie del\(\ k^{\text {th }}\) conductor del sistema. Después de que se haya resuelto tal problema de límites, es decir, se\(\ \phi(\mathbf{r})\) ha encontrado la distribución espacial en todos los puntos fuera de los conductores, es sencillo usar la ecuación (3) para encontrar la densidad de carga superficial, y finalmente la carga total

\[\ Q_{k}=\oint_{S_{k}} \sigma d^{2}r\tag{2.36}\]

de cada conductor, y por lo tanto cualquier componente de la matriz de capacitancia recíproca. A modo de ilustración, implementemos este programa por tres problemas muy simples.

(i) Condensador plano (Fig. 3). En este caso, la forma más fácil de resolver la ecuación de Laplace es usar las coordenadas lineales (cartesianas) con un eje (digamos, z), normal a las superficies del conductor — ver Fig. 6.

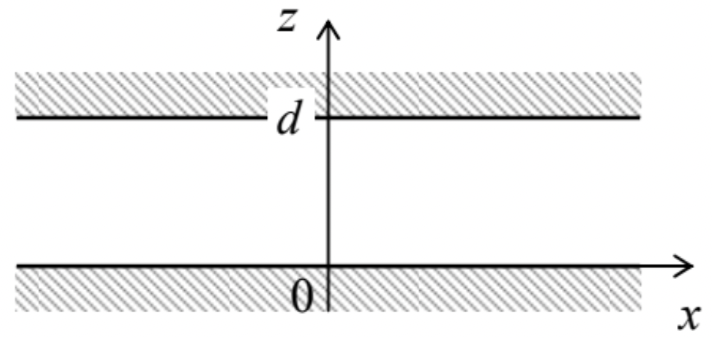Fig. 2.6. El condensador plano como sistema para la ilustración más sencilla del problema límite (35) y su solución.

En estas coordenadas, el operador de Laplace es apenas la suma de 3 segundos derivados. ²⁰ Es evidente que debido a la simetría traslacional del problema en el plano [x, y], profundamente dentro del hueco (es decir, a la distancia lateral de los bordes mucho mayor que\(\ d\)) el potencial electrostático solo puede depender de la coordenada normal a las superficies del hueco:\(\ \phi(\mathbf{r})=\phi(z)\). Para tal función, las derivadas sobre x e y desaparecen, y el problema límite (35) se reduce a una ecuación diferencial ordinaria muy simple

\[\ \frac{d^{2} \phi}{d z^{2}}(z)=0,\tag{2.37}\]

con condiciones de contorno

\[\ \phi(0)=0, \quad \phi(d)=V.\tag{2.38}\]

(En aras de la simplicidad de la notación, he utilizado la discreción de agregar una constante al potencial, para hacer que uno de los potenciales desaparezca, y también la definición (25) del voltaje\(\ V\).) La solución general de la Ec. (37) es una función lineal:\(\ \phi(z)=c_{1} z+c_{2}\), cuyos coeficientes constantes se\(\ c_{1,2}\) pueden encontrar fácilmente a partir de las condiciones límite (38). La solución final es

\[\ \phi=V \frac{z}{d}.\tag{2.39}\]

A partir de aquí el único componente distinto de cero del campo eléctrico es

\[\ E_{z}=-\frac{d \phi}{d z}=-\frac{V}{d},\tag{2.40}\]

y la carga superficial de las placas del condensador es

\[\ \sigma=\varepsilon_{0} E_{n}=\mp \varepsilon_{0} E_{z}=\pm \varepsilon_{0} \frac{V}{d},\tag{2.41}\]

donde los signos superior e inferior corresponden a la placa superior e inferior, respectivamente. Ya que\(\ \sigma\) no depende de x e y, podemos obtener las cargas completas\(\ Q_{1}=-Q_{2} \equiv Q\) de las superficies por su multiplicación por el área de hueco\(\ A\), dándonos nuevamente el resultado ya obtenido (28) para la capacitancia mutua\(\ C \equiv Q / V\). Creo que este cálculo, aunque muy fácil, puede servir como una buena ilustración del enfoque de solución de problemas de límites, que se utilizará a continuación para casos más complejos.

(ii) Capacitor de cable coaxial. El cable coaxial es un sistema de dos conductores coaxiales cilíndricos redondos, con la sección transversal mostrada en la Fig. 7.

Fig. 2.7. La sección transversal de un cable coaxial.

Evidentemente, en este caso las coordenadas cilíndricas\(\ \{\rho, \varphi, z\}\), coincidiendo el eje z con el eje común de los cilindros, son las más convenientes. Debido a la simetría axial del problema, en estas coordenadas\(\ \mathbf{E}(\mathbf{r})=\mathbf{n}_{\rho} E(\rho)\),\(\ \phi(\mathbf{r})=\phi(\rho)\), de manera que en la expresión general para el operador de Laplace ²¹ podemos tomar\(\ \partial / \partial \varphi=\partial / \partial z=0\). Como resultado, solo sobrevive el término radial del operador, y el problema de límites (35) toma la forma

\[\ \frac{1}{\rho} \frac{d}{d \rho}\left(\rho \frac{d \phi}{d \rho}\right)=0, \quad \phi(a)=V, \quad \phi(b)=0.\tag{2.42}\]

La doble integración secuencial de esta ecuación diferencial lineal ordinaria es elemental (y similar a la de la ecuación de Poisson en coordenadas esféricas, realizada en la Sec. 1.3), dando

\[\ \rho \frac{d \phi}{d \rho}=c_{1}, \quad \phi(\rho)=c_{1} \int_{a}^{\rho} \frac{d \rho^{\prime \prime}}{\rho^{\prime \prime}}+c_{2}=c_{1} \ln \frac{\rho}{a}+c_{2}.\tag{2.43}\]

Las constantes se\(\ \mathcal{C}_{1,2}\) pueden encontrar usando condiciones de contorno (42):

\[\ c_{2}=V, \quad c_{1} \ln \frac{b}{a}+c_{2}=0,\tag{2.44}\]

dando\(\ c_{1}=-V / \ln (b / a)\), de manera que la solución (43) toma la siguiente forma:

\[\ \phi(\rho)=V\left[1-\frac{\ln (\rho / a)}{\ln (b / a)}\right].\tag{2.45}\]

A continuación, para nuestra simetría axial, la expresión general para el gradiente de una función escalar se reduce a su derivada radial, de manera que

\[\ E(\rho) \equiv-\frac{d \phi(\rho)}{d \rho}=\frac{V}{\rho \ln (b / a)}.\tag{2.46}\]

Esta expresión, enchufada en la Ec. (2), nos permite encontrar la densidad de carga superficial de los conductores. Por ejemplo, para el electrodo interno

\[\ \sigma_{a}=\varepsilon_{0} E(a)=\frac{\varepsilon_{0} V}{a \ln (b / a)},\tag{2.47}\]

para que su carga completa (por unidad de longitud del sistema) sea

\[\ \frac{Q}{l}=2 \pi a \sigma_{a}=\frac{2 \pi \varepsilon_{0} V}{\ln (b / a)}.\tag{2.48}\]

(Es sencillo verificar que la carga del electrodo exterior sea igual y opuesta). De ahí que por la definición de la capacitancia mutua, su valor por unidad de longitud es

C: Cable coaxial

\[\ \frac{C}{l} \equiv \frac{Q}{l V}=\frac{2 \pi \varepsilon_{0}}{\ln (b / a)}.\tag{2.49}\]

Esta expresión muestra que la capacitancia total\(\ C\) es proporcional a la longitud del sistema\(\ l\) (if\(\ l \gg a,b\)), mientras que solo depende logarítmicamente de las dimensiones de su sección transversal. Dado que el logaritmo de un argumento muy grande es una función extremadamente lenta (a veces llamada cuasi-constante), si el conductor externo se hace muy grande\(\ (b \gg a)\), la capacitancia diverge, pero muy débilmente. Dicha divergencia logarítmica puede ser cortada por cualquier efecto adicional minúsculo, por ejemplo, por la longitud finita\(\ l\) del sistema. Esto permite obtener una estimación muy útil de la autocapacitancia de un solo cable redondo de radio\(\ a\):

\[\ C \approx \frac{2 \pi \varepsilon_{0} l}{\ln (l / a)}, \quad \text { for } l>>a.\tag{2.50}\]

Por otro lado, si el hueco\(\ d\) entre los conductores es muy estrecho:\(\ d \equiv b-a<<a\), entonces\(\ \ln (b / a) \equiv \ln (1+d / a)\) puede aproximarse como\(\ d / a\), y la Ec. (49) se reduce a\(\ C \approx 2 \pi \varepsilon_{0} al / d\), es decir, a la Ec. (28) para el condensador plano, del área apropiada\(\ A=2 \pi al\).

(iii) Capacitor esférico. Se trata de un sistema de dos conductores, con la sección transversal central similar a la del cable coaxial (Fig. 7), pero ahora con la simetría esférica más que axial. Esta simetría implica que estaríamos mejor usando coordenadas esféricas, de manera que el potencial\(\ \phi\) depende solo de una de ellas: la distancia\(\ r\) desde el centro común de los conductores:\(\ \phi(\mathbf{r})=\phi(r)\). Como ya sabemos por la Sec. 1.3, en este caso la expresión general para el operador de Laplace se reduce a su primer término (radial), de manera que la ecuación de Laplace toma la forma simple (1.47). Además, ya hemos encontrado la solución general a esta ecuación —véase la Ec. (1.50):

\[\ \phi(r)=\frac{c_{1}}{r}+c_{2},\tag{2.51}\]

Ahora actuando exactamente como arriba, es decir, determinando la constante (única esencial)\(\ c_{1}\) a partir de la condición límite\(\ \phi(a)-\phi(b)=V\), obtenemos

\[\ c_{1}=V\left(\frac{1}{a}-\frac{1}{b}\right)^{-1}, \quad \text { so that } \phi(r)=\frac{V}{r}\left(\frac{1}{a}-\frac{1}{b}\right)^{-1}+c_{2}.\tag{2.52}\]

A continuación, podemos utilizar la simetría esférica para encontrar el campo eléctrico,\(\ \mathbf{E}(\mathbf{r})=\mathbf{n}_{r} E(r)\), con

\[\ E(r)=-\frac{d \phi}{d r}=\frac{V}{r^{2}}\left(\frac{1}{a}-\frac{1}{b}\right)^{-1},\tag{2.53}\]

y de ahí sus valores en las superficies de los conductores, y luego la densidad de carga superficial\(\ \sigma\) de la Ec. (3). Por ejemplo, para la superficie del conductor interno,

\[\ \sigma_{a}=\varepsilon_{0} E(a)=\varepsilon_{0} \frac{V}{a^{2}}\left(\frac{1}{a}-\frac{1}{b}\right)^{-1},\tag{2.54}\]

para que, finalmente, para la carga completa de ese conductor obtengamos el siguiente resultado:

\[\ Q=4 \pi a^{2} \sigma=4 \pi \varepsilon_{0}\left(\frac{1}{a}-\frac{1}{b}\right)^{-1} V.\tag{2.55}\]

(Nuevamente, la carga del conductor externo es igual y opuesta.) Ahora podemos usar la definición (26) de la capacitancia mutua para obtener el resultado final

C: Capacitor esférico

\[\ C \equiv \frac{Q}{V}=4 \pi \varepsilon_{0}\left(\frac{1}{a}-\frac{1}{b}\right)^{-1} \equiv 4 \pi \varepsilon_{0} \frac{a b}{b-a}.\tag{2.56}\]

Para\(\ b \gg a\), este resultado coincide con la Ec. (17) para la autocapacitancia del conductor interno. Por otro lado, si el hueco\(\ d\) entre dos conductores es estrecho,\(\ d \equiv b-a<<a\), entonces

\[\ C=4 \pi \varepsilon_{0} \frac{a(a+d)}{d} \approx 4 \pi \varepsilon_{0} \frac{a^{2}}{d},\tag{2.57}\]

es decir, la capacitancia se acerca a la del condensador plano del área\(\ A=4 \pi a^{2}\), como debería.

Todo esto parece (y de hecho es) muy sencillo, pero contemplemos cuál fue la razón de éxitos tan fáciles. En cada uno de los casos (i) - (iii) hemos logrado encontrar tales coordenadas que tanto la ecuación de Laplace como las condiciones límite involucraron solo a una de ellas. La condición necesaria para el hecho anterior es que las coordenadas sean ortogonales. Esto significa que los tres componentes vectoriales del diferencial local dr, debido a pequeñas variaciones de las nuevas coordenadas (digamos,,\(\ dr\)\(\ d \theta\), y\(\ d \varphi\) para las coordenadas esféricas), son mutuamente perpendiculares.

---

Referencia

²⁰ Véase, por ejemplo, MA Ec. (9.1).

²¹ Véase, por ejemplo, MA Ec. (10.3).