6.3: Aproximación cuasistática y el efecto de la piel

Quizás el hecho experimental más sorprendente con respecto a los fenómenos electromagnéticos dependientes del tiempo es que a menos que sean tan rápidos que se note un nuevo efecto más de las corrientes de desplazamiento (que se discutirá en la Sec. 7 a continuación), todas las fórmulas de electrostática y magnetostática siguen siendo válidas, con la única excepción: la generalización de la Ec. (3.36) a la Ec. (5), describiendo la inducción de Faraday. Como resultado, el sistema de ecuaciones macroscópicas de Maxwell (5.109) se generaliza a

\ [\\ begin {array} {ll}
\ nabla\ veces\ mathbf {E} +\ frac {\ parcial\ mathbf {B}} {\ parcial t} =0, &\ nabla\ veces\ mathbf {H} =\ mathbf {j},\
\\ nabla\ cdot\ mathbf {D} =\ rho, &\ nabla\ cdot\ mathbf B} =0.
\ end {array}\ quad\ quad\ quad\ quad\ text {Aproximación cuasistática}\ tag {6.21}\]

(Como se desprende de las discusiones de los capítulos 3 y 5, el sistema correspondiente de ecuaciones microscópicas de Maxwell para los campos genuinos, “microscópicos”\(\ \mathbf{E}\) y\(\ \mathbf{B}\) puede obtenerse de la Ec. (21) por las sustituciones formales\(\ \mathbf{D}=\varepsilon_{0} \mathbf{E}\) y\(\ \mathbf{H}=\mathbf{B} / \mu_{0}\), y la sustitución de la carga autónoma y densidades de corriente\(\ \rho\) y\(\ \mathbf{j}\) con sus densidades completas. ¹¹) Estas ecuaciones, cuyo rango de validez se cuantificará en la Sec. 7, definen la llamada aproximación cuasistática del electromagnetismo y son suficientes para una descripción adecuada de una amplia gama de efectos físicos.

Para formar un sistema completo de ecuaciones, las ecuaciones (21) deben ser aumentadas por ecuaciones constitutivas que describan el medio en consideración. Para un conductor óhmico, pueden tomarse en las formas lineales e isotrópicas más simples (y simultáneamente, más comunes) ya discutidas en los Capítulos 4 y 5:

\[\ \mathbf{j}=\sigma \mathbf{E}, \quad \mathbf{B}=\mu \mathbf{H}.\tag{6.22}\]

Si el conductor es uniforme, es decir, los coeficientes\(\ \sigma\) y\(\ \mu\) son constantes en su interior, todo el sistema de ecuaciones (21) - (22) puede reducirse a una sola ecuación. De hecho, una sustitución secuencial de estas ecuaciones entre sí, utilizando una conocida identidad vector-álgebra ¹² en el medio, produce:

\ [\\ comenzar {alineado}
\ frac {\ parcial\ mathbf {B}} {\ parcial t} &=-\ nabla\ veces\ mathbf {E} =-\ frac {1} {\ sigma}\ nabla\ veces\ mathbf {j} =-\ frac {1} {\ sigma}\ nabla\ veces (\ nabla\ veces\ mathbf {H}) =-\ frac {1} {\ sigma\ mu}\ nabla\ times (\ nabla\ times\ mathbf {B})\ equiv-\ frac {1} {\ sigma\ mu}\ left [\ nabla (\ nabla\ cdot\ mathbf {B}) -\ nabla^ {2}\ mathbf {B}\ derecha]\\
&=\ frac {1} {\ sigma\ mu}\ nabla^ {2}\ mathbf {B}.
\ end {alineado}\ tag {6.23}\]

Así hemos llegado, sin más suposiciones, a una ecuación diferencial parcial bastante simple. Usémoslo para un análisis del llamado efecto piel, el fenómeno de autoblindaje del campo\(\ (ac)\) magnético alterno por las corrientes parásitas inducidas por el campo en un conductor óhmico. En su geometría más simple (Fig. 2a), una fuente externa (que, en este punto, no necesita especificarse) produce, cerca de una superficie plana de un conductor a granel, un campo magnético de CA espacialmente uniforme\(\ \mathbf{H}^{(0)}(t)\) paralelo a la superficie. ¹³

Fig. 6.2. (a) El efecto piel en la geometría más simple, plana, y (b) dos contornos Ampère,\(\ C_{1}\) y\(\ C_{2}\), para derivar las condiciones de\(\ \left(C_{2}\right)\) límite “macroscópicas”\(\ \left(C_{1}\right)\) y “de grano grueso” para\(\ \mathbf{H}\).

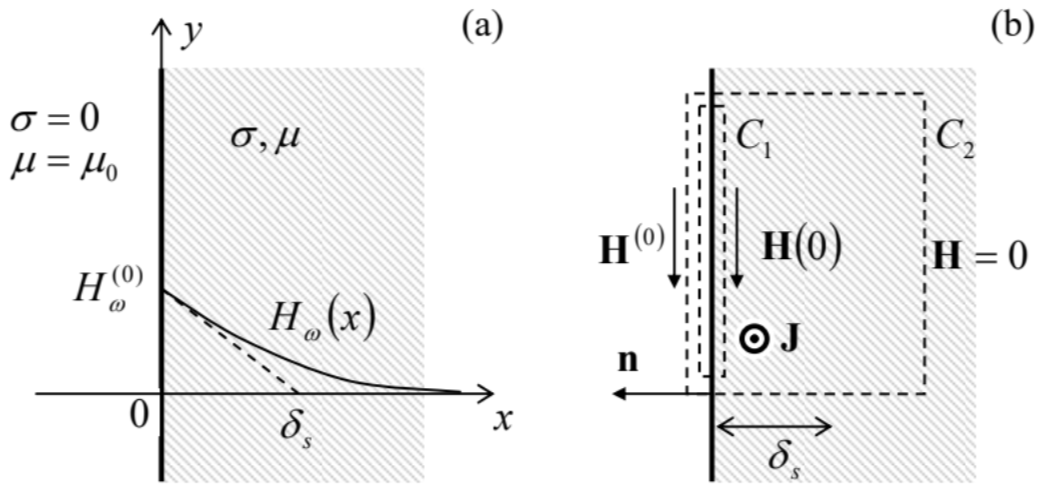
Seleccionando el sistema de coordenadas como se muestra en la Fig. 2a, podemos expresar esta condición como

\[\ \left.\mathbf{H}\right|_{x=-0}=H^{(0)}(t) \mathbf{n}_{y}.\tag{6.24}\]

La simetría traslacional de nuestro problema simple dentro del plano superficial [y, z] implica que dentro del conductor\(\ \partial / \partial y=\partial / \partial z=0\) también, e\(\ \mathbf{H}=H(x, t) \mathbf{n}_{y}\) incluso at\(\ x \geq 0\), de manera que la ecuación (23) para el interior del conductor se reduce a una ecuación diferencial para una sola función escalar\(\ H(x, t)=B(x, t) / \mu\):

\[\ \frac{\partial H}{\partial t}=\frac{1}{\sigma \mu} \frac{\partial^{2} H}{\partial x^{2}}, \quad \text { for } x \geq 0.\tag{6.25}\]

Esta ecuación puede simplificarse aún más al notar que debido a su linealidad, podemos usar el principio de superposición lineal para la dependencia temporal del campo, ¹⁴ a través de su expansión, así como el campo externo (24), en la serie de Fourier:

\ [\\ begin {array} {ll}
H (x, t) =\ suma_ {\ omega} H_ {\ omega} (x) e^ {-i\ omega t}, &\ text {for} x. \ geq 0,\\
H^ {(0)} (t) =\ suma_ {\ omega} H_ {\ omega} ^ {(0)} e^ {-i\ omega t}, &\ text {for} x=-0,
\ end {array}\ tag {6.26}\]

y argumentando que si conocemos la solución para cada componente de frecuencia de la serie, todo el campo se puede encontrar a través de la suma directa (26) de estas soluciones.

Para cada componente de frecuencia única, la ecuación (25) se reduce inmediatamente a una ecuación diferencial ordinaria para la amplitud compleja\(\ H_{\omega}(x)\): ¹⁵

\[\ -i \omega H_{\omega}=\frac{1}{\sigma \mu} \frac{d^{2}}{d x^{2}} H_{\omega}.\tag{6.27}\]

A partir de la teoría de las ecuaciones diferenciales ordinarias lineales, sabemos que la Ec. (27) tiene la siguiente solución general:

\[\ H_{\omega}(x)=H_{+} e^{\kappa_{+} x}+H_{-} e^{\kappa_{-} x},\tag{6.28}\]

donde las constantes\(\ \kappa_{\pm}\) son las raíces de la ecuación característica que se puede obtener mediante la sustitución de cualquiera de estos dos exponentes en la ecuación diferencial inicial. Para nuestro caso particular, la ecuación característica, que sigue de la Ec. (27), es

\[\ -i \omega=\frac{\kappa^{2}}{\sigma \mu}\tag{6.29}\]

y sus raíces son constantes complejas

\[\ \kappa_{\pm}=(-i \mu \omega \sigma)^{1 / 2} \equiv \pm \frac{1-i}{\sqrt{2}}(\mu \omega \sigma)^{1 / 2}.\tag{6.30}\]

Para nuestro problema, el campo no puede crecer exponencialmente a\(\ x \rightarrow+\infty\), de manera que solo uno de los coeficientes, es decir,\(\ H\_\) correspondiente al exponente en descomposición, con Re\(\ \kappa<0\) (i.e.\(\ \kappa=\kappa_-\)), puede ser diferente de cero, i.e\(\ H_{\omega}(x)=H_{\omega}(0) \exp \{\kappa_- x\}\). Para encontrar el factor constante\(\ \mathrm{H}_{\omega}(0)\), podemos integrar la ecuación macroscópica de Maxwell\(\ \nabla \times \mathbf{H}=\mathbf{j}\) a lo largo de un contorno previo a la superficie, digamos, el contorno que\(\ C_{1}\) se muestra en la Fig. 2b. La integral del lado derecho es insignificante porque la densidad de corriente independiente\(\ \mathbf{j}\) no incluye las corrientes de “superficie genuina” responsables de la permeabilidad magnética\(\ \mu\) — ver Fig. 5.12. Como resultado, obtenemos la condición de límite similar a la Ec. (5.117) para el campo magnético estacionario:\(\ H_{\tau}=\mathrm{const}\) at\(\ x=0\), i.e.

\[\ H(0, t)=H^{(0)}(t), \quad \text { i.e. } H_{\omega}(0)=H_{\omega}^{(0)},\tag{6.31}\]

para que la solución final de nuestro problema pueda ser representada como

\[\ H_{\omega}(x)=H_{\omega}^{(0)} \exp \left\{-\frac{x}{\delta_{s}}\right\} \exp \left\{-i\left(\omega t-\frac{x}{\delta_{s}}\right)\right\},\tag{6.32}\]

donde la constante\(\ \delta_{\underline{s}}\), con la dimensión de longitud, se llama profundidad de piel:

\[\ \delta_{\mathrm{s}} \equiv-\frac{1}{\operatorname{Re} \kappa_{-}}=\left(\frac{2}{\mu \sigma \omega}\right)^{1 / 2}.\quad\quad\quad\quad\text{Skin depth}\tag{6.33}\]

Esta solución describe el efecto piel: la penetración del campo magnético ac, y las corrientes parásitas\(\ \mathbf{j}\), en un conductor solo a una profundidad finita del orden de\(\ \delta_{\mathrm{s}}\). ¹⁶ Permítanme dar algunos ejemplos numéricos de esta profundidad: para cobre a temperatura ambiente,\(\ \delta_{\mathrm{s}} \approx 1\) cm a la frecuencia de distribución de energía de CA de 60 Hz, y es del orden de solo 1\(\ \mu \mathrm{m}\) a unos pocos GHz, es decir, a frecuencias típicas de señales de teléfonos celulares y microondas de cocina magnetrones. Por otro lado, para el agua ligeramente salada,\(\ \delta_{\mathrm{s}}\) está cerca de 250 m a tan solo 1 Hz (con implicaciones significativas para las radiocomunicaciones con submarinos), y del orden de 1 cm a unos pocos GHz (explicando, en particular, el calentamiento no uniforme de un tazón de sopa en un horno de microondas).

Para completar la discusión sobre el efecto piel, consideremos qué sucede con las corrientes parásitas inducidas ¹⁷ y el campo eléctrico en este efecto. Al derivar nuestra ecuación básica (23), hemos utilizado, en particular, relaciones\(\ \mathbf{j}=\nabla \times \mathbf{H}=\nabla \times \mathbf{B} / \mu\), y\(\ \mathbf{E}=\mathbf{j} / \sigma\). Dado que una diferenciación espacial de un exponente produce un exponente similar, el campo eléctrico y la densidad de corriente tienen la misma dependencia espacial que el campo magnético, es decir, penetran dentro del conductor solo por distancias del orden de\(\ \delta_{\mathrm{s}}(\omega)\), pero sus vectores se dirigen perpendicularmente a\(\ \mathbf{B}\), mientras sigue siendo paralelo a la superficie del conductor:

\[\ \mathbf{j}_{\omega}(x)=\kappa_{-} H_{\omega}(x) \mathbf{n}_{z}, \quad \mathbf{E}_{\omega}(x)=\frac{\kappa_{-}}{\sigma} H_{\omega}(x) \mathbf{n}_{z} .\tag{6.34}\]

Podemos usar estas expresiones para calcular la densidad de potencia promediada en el tiempo (4.39) de la disipación de energía, para el caso importante de un campo sinusoidal (“monocromático”)\(\ H(x, t)=\left|H_{\omega}(x)\right| \cos (\omega t+\varphi)\), y por lo tanto corrientes de Foucault sinusoidales\(\ j(x, t)=|j _{\omega}(x)| \cos \left(\omega t+\varphi^{\prime}\right)\):

\[\ \bar{\mathscr{I}}(x)=\frac{\overline{j^{2}(x, t)}}{\sigma}=\frac{\left|j_{\omega}(x)\right|^{2} \overline{\cos ^{2}\left(\omega t+\varphi^{\prime}\right)}}{\sigma}=\frac{\left|j_{\omega}(x)\right|^{2}}{2 \sigma}=\frac{\left|\kappa_{-}\right|^{2}\left|H_{\omega}(x)\right|^{2}}{2 \sigma}=\frac{\left|H_{\omega}(x)\right|^{2}}{\delta_{\mathrm{s}}^{2} \sigma} \equiv \frac{H_{\omega}(x) H_{\omega}^{*}(x)}{\delta_{\mathrm{s}}^{2} \sigma}.\tag{6.35}\]

Ahora la integración (elemental) de esta expresión a lo largo del eje x (a través de toda la profundidad de la piel), utilizando la ley exponencial (6.32), nos da la siguiente potencia promedio de la pérdida de energía por unidad de área:

\[\ \text{Energy loss at skin effect}\quad\quad\quad\quad\frac{d \overline{\mathscr{P}}}{d A} \equiv \int_{0}^{\infty} \bar{\mathscr{I}}(x) d x=\frac{1}{2 \delta_{\mathrm{s}} \sigma}\left|H_{\omega}^{(0)}\right|^{2} \equiv \frac{\mu \omega \delta_{\mathrm{s}}}{4}\left|H_{\omega}^{(0)}\right|^{2}.\tag{6.36}\]

Utilizaremos ampliamente esta expresión en el próximo capítulo para calcular las pérdidas de energía en guías de ondas de microondas y resonadores con paredes conductoras (prácticamente, metálicas), y por ahora solo notemos que de acuerdo con las ecuaciones (33) y (36), para una amplitud de campo magnético fijo, las pérdidas crecen con la frecuencia como\(\ \omega^{1 / 2}\).

Una observación más importante sobre las ecuaciones (34): integrando la primera de ellas sobre\(\ x\), con la ayuda de la ecuación (32), podemos ver que la densidad lineal\(\ \mathbf{J}\) de las corrientes superficiales (medidas en A/m), se relaciona simple y fundamentalmente con el campo magnético aplicado:

\[\ \mathbf{J}_{\omega} \equiv \int_{0}^{\infty} \mathbf{j}_{\omega}(x) d x=H_{\omega}^{(0)} \mathbf{n}_{z}.\tag{6.37}\]

Como esta relación no tiene ningún factor dependiente de la frecuencia, podemos resumirla para todos los componentes de frecuencia y obtener una relación universal

\[\ \mathbf{J}(t)=H^{(0)}(t) \mathbf{n}_{z} \equiv H^{(0)}(t)\left(-\mathbf{n}_{y} \times \mathbf{n}_{x}\right)=\mathbf{H}^{(0)}(t) \times\left(-\mathbf{n}_{x}\right)=\mathbf{H}^{(0)}(t) \times \mathbf{n},\tag{6.38a}\]

(donde\(\ \mathbf{n}=-\mathbf{n}_{x}\) es la normal exterior a la superficie — ver Fig. 2b) o, en una forma diferente,

\[\ \Delta \mathbf{H}(t)=\mathbf{n} \times \mathbf{J}(t),\quad\quad\quad\quad\text{Coarse-grain boundary relation}\tag{6.38b}\]

donde\(\ \Delta \mathbf{H}\) está el cambio completo del campo a través de la capa de piel. Esta relación simple de grano grueso (independiente de la elección de los ejes de coordenadas), es independiente de las relaciones constitutivas utilizadas (22), y de ninguna manera es ocasional. En efecto, se puede obtener fácilmente de la ley Macroscópica Ampère (5.116), aplicada a un contorno dibujado alrededor de un fragmento de la superficie, extendiéndose por debajo de ella sustancialmente más profundo que la profundidad de la piel — ver el contorno\(\ C_{2}\) en la Fig. 2b, y es válido independientemente de la ley exacta de la penetración en el campo.

Para el efecto piel, esta relación fundamental entre la densidad de corriente lineal y el campo magnético externo implica que la implementación del efecto piel no requiere necesariamente una fuente de campo magnético de CA dedicada. Por ejemplo, el efecto tiene lugar en cualquier cable que lleve una corriente de CA, lo que lleva a una concentración de corriente en una lámina de superficie de espesor\(\ \sim \delta_{\mathrm{s}}\). (Por supuesto, el análisis cuantitativo de este problema en un alambre con una sección transversal arbitraria puede ser técnicamente complicado, porque requiere resolver la Eq. (23) para una geometría 2D; incluso para la sección transversal redonda, la solución involucra las funciones de Bessel — ver Problema 9.) En este caso, el campo magnético ac fuera del conductor, que aún obedece a la ecuación (38), puede interpretarse mejor como el efecto, más que la razón, del flujo de corriente ac.

Por último, tenga en cuenta la validez limitada de todos los resultados anteriores. Primero, para que la aproximación cuasistática sea válida, la frecuencia de campo no\(\ \omega\) debe ser demasiado alta, por lo que los efectos de la corriente de desplazamiento son despreciables. (Nuevamente, esta condición se cuantificará en la Sec. 7 a continuación; mostrará que para los metales, la condición es violada sólo a frecuencias extremadamente altas arriba)\(\ \sim 10^{18} \mathrm{~s}^{-1}\). Un límite superior más práctico\(\ \omega\) es que la profundidad de la piel\(\ \delta_{\mathrm{s}}\) debe permanecer mucho mayor que la trayectoria libre media de los portadores\(\ l\) de carga, ¹⁸ porque más allá de este punto, la relación entre los vectores\(\ \mathbf{j}(\mathbf{r})\) y\(\ \mathbf{E}(\mathbf{r})\) se vuelve esencialmente no local. Tanto la teoría como el experimento muestran que a\(\ \delta_{\mathrm{s}}\) continuación\(\ l\), el efecto de la piel persiste, pero adquiere una dependencia de frecuencia ligeramente diferente de la Ec. (33):\(\ \delta_{\mathrm{s}} \propto \omega^{-1 / 3}\) en lugar de\(\ \omega^{-1 / 2}\). Este llamado efecto anómalo de la piel tiene aplicaciones útiles, por ejemplo, para mediciones experimentales de la superficie Fermi de metales. ¹⁹

---

Referencia

¹¹ Obviamente, en el espacio libre la última sustitución es innecesaria, porque todas las cargas y corrientes pueden tratarse como “independientes”.

¹² Véase, por ejemplo, MA Ec. (11.3).

¹³ Debido a la simple relación lineal\(\ \mathbf{B}=\mu \mathbf{H}\) entre los campos\(\ \mathbf{B}\) y\(\ \mathbf{H}\), no importa demasiado cuál de
ellos se utilice para la solución de este problema, con una ligera preferencia por\(\ \mathbf{H}\), debido a la simplicidad de la Ec. (5.117) — el único límite condición relevante para esta geometría simple.

¹⁴ Otra forma importante de explotar la linealidad de la ecuación (6.25) es utilizar el enfoque de función espacio-temporal de Green para explorar la dependencia de sus soluciones en diversas condiciones iniciales. Desafortunadamente, por falta de tiempo, tengo que dejar un análisis de esta oportunidad para el ejercicio del lector.

¹⁵ Permítanme esperar que el lector no se vea intimidado por el (muy conveniente) uso de variables tan complejas para describir campos reales; sus partes imaginarias siempre desaparecen en la suma final (26). Por ejemplo, si el campo externo es puramente sinusoidal, con la frecuencia real (positiva)\(\ \omega\), cada suma en la Ec. (26) tiene apenas dos términos, con amplitudes complejas\(\ H_{\omega}\) y\(\ H_{-\omega}=H_{\omega}^{*}\), de manera que su suma sea siempre real. (Para una discusión más detallada de este tema, véase, por ejemplo, CM Sec. 5.1.)

¹⁶ Permítanme esperar que la intuición física del lector haga evidente que el campo ac penetra en una muestra de cualquier forma por una distancia similar.

¹⁷ El carácter de bucle (vórtice) de las líneas de corriente inducidas, responsables del término “eddy”, no es muy evidente en la geometría 1D explorada anteriormente, con las corrientes cercanas a la superficie (Fig. 2b) en bucle solo implícitamente, at\(\ z \rightarrow \pm \infty\).

¹⁸ Una breve discusión sobre el camino libre medio se puede encontrar, por ejemplo, en SM Capítulo 6. En metales muy limpios a temperaturas muy bajas,\(\ \delta_{\mathrm{s}}\) puede acercarse\(\ l\) a frecuencias tan bajas como ~1 GHz, pero a temperatura ambiente, el cruce del efecto normal al anómalo de la piel se lleva a cabo solo a ~ 100 GHz.

¹⁹ Véase, e.g., A. Abrikosov, Introducción a la Teoría de los Metales Normales, Prensa Académica, 1972.