7.2: Atenuación y dispersión

Permítanme iniciar la discusión de los efectos de dispersión y atenuación considerando un caso particular de evolución temporal de la polarización eléctrica\(\ \mathbf{P}(t)\) de un medio diluido, no polar, con interacción insignificante entre sus dipolos elementales\(\ \mathbf{p}(t)\). Como se discutió en la Sec. 3.3, en este caso, el campo eléctrico local que actúa sobre cada dipolo elemental, es igual al campo macroscópico\(\ \mathbf{E}(t)\). Entonces, el momento dipolo\(\ \mathbf{p}(t)\) puede ser causado no sólo por los valores del campo E en el mismo momento del tiempo\(\ (t)\), sino también los de los momentos anteriores,\(\ t<t’\). Debido al principio de superposición lineal, la polarización macroscópica\(\ \mathbf{P}(t)=n \mathbf{p}(t)\) debe ser una suma (o más bien una integral) de los valores de\(\ \mathbf{E}\left(t^{\prime}\right)\) en todos los momentos\(\ t^{\prime} \leq t\), ponderados por alguna función de\(\ t\) y\(\ t’\): ⁸

\[\ P(t)=\int_{-\infty}^{t} E\left(t^{\prime}\right) G\left(t, t^{\prime}\right) d t^{\prime}.\quad\quad\quad\quad\text{Temporal Green’s function}\tag{7.21}\]

La condición\(\ t^{\prime} \leq t\), que está implícita en esta relación, expresa un principio clave de la física, la relación causal entre una causa (en nuestro caso, el campo eléctrico aplicado a cada dipolo) y su efecto (la polarización que crea). La función\(\ G\left(t, t^{\prime}\right)\) se llama la función temporal del Verde para la
polarización eléctrica. ⁹ Para revelar su sentido físico, consideremos el caso cuando el campo aplicado\(\ E(t)\) es un pulso muy corto en este momento\(\ t_{0}<t\), que puede estar bien aproximado con la función delta de Dirac:

\[\ E(t)=\delta\left(t-t^{\prime \prime}\right).\tag{7.22}\]

Entonces la Eq. (21) rinde justamente\(\ P(t)=G\left(t, t^{\prime \prime}\right)\), de manera que la función del Verde\(\ G\left(t, t^{\prime}\right)\) es solo la polarización en el momento\(\ t\), creada por un\(\ \delta \text {-functional }\) pulso unitario del campo aplicado en el momento\(\ t^{\prime}\) (Fig. 4).

Fig. 7.4. Un ejemplo de la función temporal del Green para la polarización eléctrica (esquemáticamente).

¿Cuáles son las propiedades generales de la función temporal de Green? En primer lugar, la función es real, ya que el momento dipolo\(\ \mathbf{p}\) y por lo tanto la polarización\(\ \mathbf{P}=n \mathbf{p}\) son reales — ver Ec. (3.6). A continuación, para sistemas sin “memoria” interna infinita,\(\ G\) debería tender a cero en\(\ t-t^{\prime} \rightarrow \infty\), aunque el tipo de este enfoque (por ejemplo, si la función G oscila acercándose a cero, como en la Fig. 4, o no) depende de las propiedades del medio. Finalmente, si los parámetros del medio no cambian en el tiempo, la respuesta de polarización a un pulso de campo eléctrico debe depender no de su temporización absoluta, sino solo de la diferencia de tiempo\(\ \theta \equiv t-t^{\prime}\) entre el pulso y los instantes de observación, es decir, la Ec. (21) se reduce a

\[\ P(t)=\int_{-\infty}^{t} E\left(t^{\prime}\right) G\left(t-t^{\prime}\right) d t^{\prime} \equiv \int_{0}^{\infty} E(t-\theta) G(\theta) d \theta.\tag{7.23}\]

Para una forma de onda sinusoidal,\(\ E(t)=\operatorname{Re}\left[E_{\omega} e^{-i \omega t}\right]\), esta ecuación rinde

\[\ P(t)=\operatorname{Re} \int_{0}^{\infty} E_{\omega} e^{-i \omega(t-\theta)} G(\theta) d \theta \equiv \operatorname{Re}\left[\left(E_{\omega} \int_{0}^{\infty} G(\theta) e^{i \omega \theta} d \theta\right) e^{-i \omega t}\right].\tag{7.24}\]

La expresión en los últimos paréntesis no es, por supuesto, otra cosa que la compleja amplitud\(\ P_{\omega}\) de la polarización. Esto significa que aunque la relación lineal estática (3.43),\(\ P=\chi_{\mathrm{e}} \varepsilon_{0} E\), no es válida para un proceso arbitrario dependiente del tiempo, aún podemos mantener su análogo de Fourier,

\[\ P_{\omega}=\chi_{\mathrm{e}}(\omega) \varepsilon_{0} E_{\omega}, \quad \text { with } \chi_{\mathrm{e}}(\omega) \equiv \frac{1}{\varepsilon_{0}} \int_{0}^{\infty} G(\theta) e^{i \omega \theta} d \theta,\tag{7.25}\]

para cada componente sinusoidal del proceso, utilizándolo como definición de la susceptibilidad eléctrica dependiente de la frecuencia\(\ \chi_{\mathrm{e}}(\omega)\). De manera similar, la permitividad eléctrica dependiente de la frecuencia puede definirse usando el análogo de Fourier de la Ec. (3.46):

\[\ D_{\omega} \equiv \varepsilon(\omega) E_{\omega}.\quad\quad\quad\quad \text{Complex electric permittivity}\tag{7.26a}\]

Entonces, según la definición (3.33), la permitividad se relaciona con la función temporal del Verde por la transformada habitual de Fourier:

\[\ \varepsilon(\omega) \equiv \varepsilon_{0}+\frac{P_{\omega}}{E_{\omega}}=\varepsilon_{0}+\int_{0}^{\infty} G(\theta) e^{i \omega \theta} d \theta.\tag{7.26b}\]

Esta relación demuestra que\(\ \varepsilon(\omega)\) puede ser compleja,

\[\ \varepsilon(\omega)=\varepsilon^{\prime}(\omega)+i \varepsilon^{\prime \prime}(\omega), \quad \text { with } \varepsilon^{\prime}(\omega)=\varepsilon_{0}+\int_{0}^{\infty} G(\theta) \cos \omega \theta d \theta, \quad \varepsilon^{\prime \prime}(\omega)=\int_{0}^{\infty} G(\theta) \sin \omega \theta d \theta,\tag{7.27}\]

y que su parte real\(\ \varepsilon^{\prime}(\omega)\) es siempre una función par de frecuencia, mientras que la parte imaginaria\(\ \varepsilon^{\prime \prime}(\omega)\) es una función
impar de\(\ \omega\). Obsérvese que aunque la relación causal particular (21) entre\(\ P(t)\) y\(\ E(t)\) está condicionada por la independencia del dipolo elemental, la permitividad eléctrica compleja dependiente de la frecuencia\(\ \varepsilon(\omega)\) puede introducirse, de manera similar, si dos combinaciones lineales cualesquiera de estas variables están relacionadas por una fórmula similar. Argumentos absolutamente similares muestran que las propiedades magnéticas de un medio lineal isotrópico pueden caracterizarse con una permeabilidad compleja dependiente de la frecuencia\(\ \mu(\omega)\).

Ahora reescribiendo las ecuaciones (1) para las amplitudes complejas de los campos a una frecuencia particular, podemos repetir todos los cálculos de la Sec. 1, y verificar que todos sus resultados son válidos para ondas monocromáticas incluso para una dispersiva (¡pero necesariamente lineal!) mediano. En particular, las ecuaciones (7) y (13) se convierten ahora

\[\ Z(\omega)=\left(\frac{\mu(\omega)}{\varepsilon(\omega)}\right)^{1 / 2}, \quad k(\omega)=\omega[\varepsilon(\omega) \mu(\omega)]^{1 / 2},\quad\quad\quad\quad\text{Complex } Z \text{ and } k\tag{7.28}\]

de manera que la impedancia de onda y el número de onda pueden ser ambas funciones complejas de frecuencia. ¹⁰

Este hecho tiene importantes consecuencias para la propagación de ondas electromagnéticas. Primero, enchufando la representación del número de onda compleja como la suma de sus partes reales e imaginarias,\(\ k(\omega) \equiv k^{\prime}(\omega)+ik^{\prime\prime}(\omega)\), en la ecuación (11):

\[\ f=\operatorname{Re}\left\{f_{\omega} e^{i[k(\omega) z-\omega t]}\right\}=e^{-k^{\prime \prime}(\omega) z} \operatorname{Re}\left\{f_{\omega} e^{i\left[k^{\prime}(\omega) z-\omega t\right]}\right\},\tag{7.29}\]

vemos que\(\ k^{\prime \prime}(\omega)\) describe la tasa de atenuación de onda en el medio a la frecuencia\(\ \omega\). ¹¹ En segundo lugar, si la forma de onda no es sinusoidal (y por lo tanto debe representarse como una suma de varios/muchos componentes sinusoidales), la dependencia de frecuencia de\(\ k^{\prime}(\omega)\) proporciona la dispersión de la onda, es decir, la deformación de la forma de onda en la propagación, debido a que la velocidad de propagación (4) de ondas componentes ahora es diferente. ¹²

Como ejemplo de tal medio dispersivo, consideremos un modelo de oscilador Lorentz simple pero muy representativo. ¹³ En sistemas atómicos o moleculares diluidos (e.g., gases), los electrones responden al campo eléctrico externo especialmente fuertemente cuando la frecuencia\(\ \omega\) está cerca de ciertas frecuencias\(\ \omega_{j}\) correspondientes al espectro de transiciones interestatales cuánticas de un solo átomo/molécula. Se puede obtener una descripción fenomenológica aproximada de este comportamiento a partir de un modelo clásico de varios osciladores armónicos impulsados externamente, generalmente con amortiguación distinta de cero. Para un solo oscilador, impulsado por la fuerza del campo eléctrico\(\ F(t)=q E(t)\), podemos escribir la ley de\(\ 2^{\text {nd }}\) Newton como

\[\ m\left(\ddot{x}+2 \delta_{0} \dot{x}+\omega_{0}^{2} x\right)=q E(t),\tag{7.30}\]

donde\(\ \omega_{0}\) es la propia frecuencia del oscilador, y\(\ \delta_{0}\) su coeficiente de amortiguamiento. Para el campo eléctrico de una onda monocromática\(\ E(t)=\operatorname{Re}\left[E_{\omega} \exp \{-i \omega t\}\right]\),, podemos buscar una solución particular de oscilación forzada de esta ecuación en una forma similar\(\ x(t)=\operatorname{Re}\left[x_{\omega} \exp \{-i \omega t\}\right]\). ¹⁴ Al enchufar esta solución en la ecuación (30), encontramos fácilmente la compleja amplitud de estas oscilaciones:

\[\ x_{\omega}=\frac{q}{m} \frac{E_{\omega}}{\left(\omega_{0}^{2}-\omega^{2}\right)-2 i \omega \delta_{0}}.\tag{7.31}\]

Usando este resultado para calcular la amplitud compleja del momento dipolar como\(\ p_{\omega}=q x_{\omega}\), y luego la polarización eléctrica\(\ P_{\omega}=n p_{\omega}\) de un medio diluido con osciladores\(\ n\) independientes para unidad de volumen, por su permitividad dependiente de la frecuencia (26) obtenemos

\[\ \text{Lorentz oscillator model}\quad\quad\quad\quad\varepsilon(\omega)=\varepsilon_{0}+n \frac{q^{2}}{m} \frac{1}{\left(\omega_{0}^{2}-\omega^{2}\right)-2 i \omega \delta_{0}}.\tag{7.32}\]

Este resultado puede generalizarse fácilmente al caso cuando el sistema tiene varios tipos de osciladores con diferentes masas y frecuencias:

\[\ \varepsilon(\omega)=\varepsilon_{0}+n q^{2} \sum_{j} \frac{f_{j}}{m_{j}\left[\left(\omega_{j}^{2}-\omega^{2}\right)-2 i \omega \delta_{j}\right]},\tag{7.33}\]

donde\(\ f_{j} \equiv n_{j} / n\) está la fracción de osciladores con frecuencia\(\ \omega_{j}\), de manera que la suma de todos\(\ f_{j}\) es igual a 1. La Figura 5 muestra un comportamiento típico de las partes real e imaginaria de la constante dieléctrica compleja, descrita por la Ec. (33), como funciones de frecuencia. El efecto de las resonancias del oscilador es claramente visible, y domina la respuesta de los medios en\(\ \omega \approx \omega_{j}\), especialmente en el caso de baja amortiguación,\(\ \delta_{j}<<\omega_{j}\). Obsérvese que en el límite de baja amortiguación, la parte imaginaria de la constante dieléctrica\(\ \varepsilon^{\prime \prime}\)\(\ k^{\prime \prime}\), y de ahí la atenuación de onda, son insignificantemente pequeñas en todas las frecuencias además de pequeñas proximidades de frecuencias\(\ \omega_{j}\), donde la derivada\(\ d \varepsilon^{\prime}(\omega) / d \omega\) es negativa. ¹⁵ Así, para un sistema de osciladores débilmente amortiguados, la ecuación (33) puede aproximarse bien mediante una suma de singularidades (“polos”):

\[\ \varepsilon(\omega) \approx \varepsilon_{0}+n \frac{q^{2}}{2} \sum_{j} \frac{f_{j}}{m_{j} \omega_{j}\left(\omega_{j}-\omega\right)}, \quad \text { for } \delta_{j}<<\left|\omega-\omega_{j}\right|<<\left|\omega_{j}-\omega_{j^{\prime}}\right|.\tag{7.34}\]

Fig. 7.5. Dependencia típica de la frecuencia de las partes real e imaginaria de la permitividad eléctrica compleja, según el modelo generalizado del oscilador Lorentz.

Este resultado es especialmente importante porque, según la mecánica cuántica, ¹⁶ Eq. (34) (con todos\(\ m_{j}\) iguales) también es válido para un conjunto de sistemas cuánticos similares que no interactúan (¡cuya dinámica puede ser completamente diferente a la de un oscilador armónico!) , siempre que\(\ \omega_{j}\) se sustituyan por frecuencias
de posibles transiciones interestatales cuánticas, y los coeficientes\(\ f_{j}\) se sustituyan por las llamadas intensidades del oscilador de las transiciones, que obedecen a la misma regla de suma,\(\ \sum_{j} f_{j}=1\).

At\(\ \omega \rightarrow 0\), la parte imaginaria de la permitividad (33) también se desvanece (para cualquier\(\ \delta_{j}\)), mientras que su parte real se acerca a su valor electrostático (“dc”)

\[\ \varepsilon(0)=\varepsilon_{0}+q^{2} \sum_{j} \frac{n_{j}}{m_{j} \omega_{j}^{2}}.\tag{7.35}\]

Tenga en cuenta que de acuerdo con la ecuación (30), el denominador en la ecuación (35) es solo la constante elástica efectiva\(\ \kappa_{j}=m_j\omega_j^2\) del\(\ j^{\text {th }}\) oscilador, de manera que las masas del oscilador\(\ m_{j}\) como tales en realidad (y de manera natural) no están involucradas en la respuesta dieléctrica estática.

En el límite opuesto de frecuencias muy altas,\(\ \omega >> \omega_{j}, \delta_{j}\), la permitividad también se vuelve real y puede representarse como

\[\ \varepsilon(\omega)=\varepsilon_{0}\left(1-\frac{\omega_{\mathrm{p}}^{2}}{\omega^{2}}\right), \quad \text { where } \omega_{\mathrm{p}}^{2} \equiv \frac{q^{2}}{\varepsilon_{0}} \sum_{j} \frac{n_{j}}{m_{j}}\quad\quad\quad\quad \varepsilon(\omega) \text{ in plasma} \tag{7.36}\]

Este resultado es muy importante, porque también es válido en todas las frecuencias si todas\(\ \omega_{j}\) y\(\ \delta_{j}\) desaparecen, por ejemplo para gases de partículas de carga libre, en particular para plasmas —gases atómicos ionizados, siempre que los efectos de colisión de iones sean insignificantes. (Es por ello que el parámetro\(\ \omega_{\mathrm{p}}\) definido por la Ec. (36) se llama la frecuencia de plasma.) Típicamente, el plasma en su conjunto es neutro, es decir, la densidad\(\ n\) de iones atómicos positivos es igual a la de los electrones libres. Dado que la relación\(\ n_{j} / m_{j}\) para los electrones es mucho mayor que la de los iones, la fórmula general (36) para la frecuencia de plasma suele ser bien aproximada mediante la siguiente expresión simple:

\[\ \omega_{\mathrm{p}}^{2}=\frac{n e^{2}}{\varepsilon_{0} m_{\mathrm{e}}}.\tag{7.37}\]

Esta expresión tiene un sentido físico simple: la constante elástica efectiva\(\ \kappa_{\mathrm{ef}} \equiv m_{\mathrm{e}} \omega_{\mathrm{p}}^{2}=n e^{2} / \varepsilon_{0}\) describe la fuerza Coulomb que aparece cuando el subsistema electrónico del plasma se desplaza, como un todo, de su subsistema de iones positivos, violando así la electroneutralidad. (En efecto, consideremos un desplazamiento tan pequeño,\(\ \Delta x\), perpendicular a la superficie plana de una losa ancha y plana llena de plasma. Las cargas de iones no compensadas, con densidades superficiales iguales y opuestas\(\ \sigma=\pm e n \Delta x\), que aparecen en las superficies de la losa, crean en su interior, de acuerdo con la Ec. (2.3), un campo eléctrico uniforme con\(\ E_{x}=e n \Delta x / \varepsilon_{0}\). Este campo ejerce fuerza\(\ -e E=-\left(n e^{2} / \varepsilon_{0}\right) \Delta x=-\kappa_{\mathrm{ef}} \Delta x\) sobre cada electrón, tirando de él de nuevo a su posición de equilibrio.) Por lo tanto, no hay sorpresa que la función\(\ \varepsilon(\omega)\) dada por la ecuación (36) se desvanezca a\(\ \omega=\omega_{\mathrm{p}}\): a esta frecuencia de resonancia, el campo eléctrico de polarización E puede oscilar, es decir, tener una amplitud distinta de cero\(\ E_{\omega}=D_{\omega} / \varepsilon(\omega)\), incluso en ausencia de fuerzas externas inducidas por externas (autónomas) cargas, es decir, en ausencia del campo D estas cargas inducen — véase la Ec. (3.32).

El comportamiento de las ondas electromagnéticas en un medio que obedece a la Ec. (36), es muy notable. Si la frecuencia de onda\(\ \omega\) es superior\(\ \omega_{\mathrm{p}}\), la constante dieléctrica\(\ \varepsilon(\omega)\), y por lo tanto el número de onda (28) son positivos y reales, y las ondas se propagan sin atenuación, siguiendo la relación de dispersión,

\[\ \text{Plasma dispersion relation}\quad \quad\quad\quad k(\omega)=\omega\left[\varepsilon(\omega) \mu_{0}\right]^{1 / 2}=\frac{1}{c}\left(\omega^{2}-\omega_{\mathrm{p}}^{2}\right)^{1 / 2},\tag{7.38}\]

que se muestra en la Fig. 6.

Fig. 7.6. La ley de dispersión de plasma (línea continua) en comparación con la dispersión lineal en el espacio libre (línea discontinua).

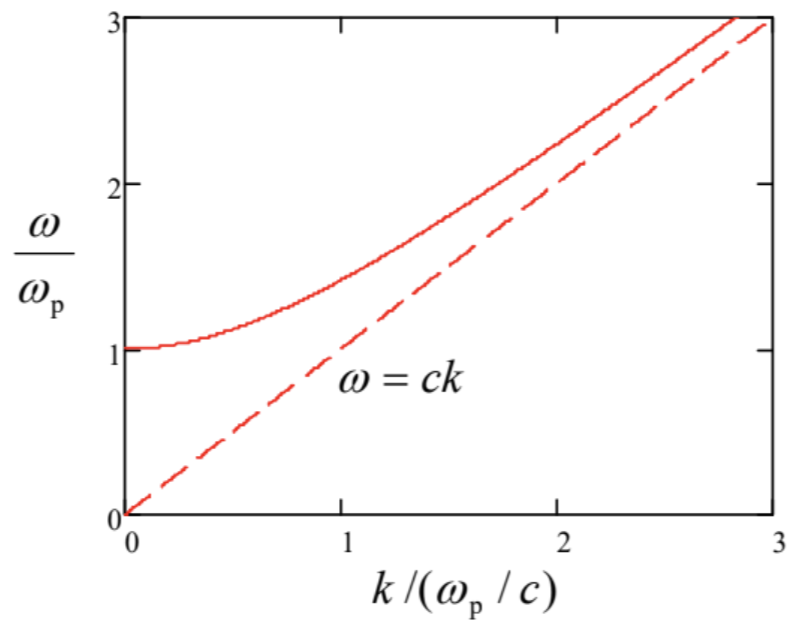
En\(\ \omega \rightarrow \omega_{\mathrm{p}}\) el número de onda\(\ k\) tiende a cero. Más allá de ese punto (es decir, at\(\ \omega<\omega_{\mathrm{p}}\)), todavía podemos usar la
ecuación (38), pero es instrumental para reescribirla en la forma matemáticamente equivalente

\[\ k(\omega)=\frac{i}{c}\left(\omega_{\mathrm{p}}^{2}-\omega^{2}\right)^{1 / 2}=\frac{i}{\delta}, \quad \text { where } \delta \equiv \frac{c}{\left(\omega_{\mathrm{p}}^{2}-\omega^{2}\right)^{1 / 2}}.\tag{7.39}\]

Dado que\(\ \omega<\omega_{\mathrm{p}}\) el parámetro así definido\(\ \delta\) es real, la Ec. (29) muestra que el campo electromagnético disminuye exponencialmente con la distancia:

\[\ f=\operatorname{Re} f_{\omega} e^{i(k z-\omega t)} \equiv \exp \left\{-\frac{z}{\delta}\right\} \operatorname{Re} f_{\omega} e^{-i \omega t}.\tag{7.40}\]

¿Significa esto que la onda está siendo absorbida en el plasma? Responder a esta pregunta es un buen pretexto para calcular el promedio de tiempo del vector Poynting\(\ \mathbf{S}=\mathbf{E} \times \mathbf{H}\) de una onda electromagnética monocromática en un medio dispersivo arbitrario (pero aún lineal e isotrópico). Primero, detallemos las dependencias de tiempo de los campos reales:

\[\ E(t)=\operatorname{Re}\left[E_{\omega} e^{-i \omega t}\right] \equiv \frac{1}{2}\left[E_{\omega} e^{-i \omega t}+\text { c.c. }\right], \quad H(t)=\operatorname{Re}\left[H_{\omega} e^{-i \omega t}\right] \equiv \frac{1}{2}\left[\frac{E_{\omega}}{Z(\omega)} e^{-i \omega t}+\text { c.c. }\right] .\tag{7.41}\]

Ahora, un cálculo sencillo rinde ¹⁷

\[\ \bar{S}=\overline{E(t) H(t)}=\frac{E_{\omega} E_{\omega}^{*}}{4}\left[\frac{1}{Z(\omega)}+\frac{1}{Z^{*}(\omega)}\right] \equiv \frac{E_{\omega} E_{\omega}^{*}}{2} \operatorname{Re} \frac{1}{Z(\omega)} \equiv \frac{\left|E_{\omega}\right|^{2}}{2} \operatorname{Re}\left[\frac{\varepsilon(\omega)}{\mu(\omega)}\right]^{1 / 2}.\tag{7.42}\]

Apliquemos esta importante fórmula general a nuestro sencillo modelo de plasma en\(\ \omega<\omega_{\mathrm{p}}\). En este caso, la permeabilidad magnética es igual\(\ \mu_{0}\),\(\ \mu(\omega)=\mu_{0}\) es decir, es positiva y real, mientras que\(\ \varepsilon(\omega)\) es real y negativa, por lo que\(\ 1 / Z(\omega)=[\varepsilon(\omega) / \mu(\omega)]^{1 / 2}\) es puramente imaginaria, y el vector Poynting promedio (42) desaparece. Esto significa que la energía, en promedio, no fluye a lo largo del eje z. Entonces, las ondas con no\(\ \omega<\omega_\mathrm{p}\) son absorbidas en plasma. (De hecho, el modelo Lorentz con\(\ \delta_{j}=0\) no describe ningún mecanismo de disipación de energía.) En cambio, como veremos en la siguiente sección, las ondas se reflejan más bien desde el límite del plasma.

Obsérvese también que en el límite\(\ \omega<<\omega_{\mathrm{p}}\), la ecuación (39) rinde

\[\ \delta \rightarrow \frac{c}{\omega_{\mathrm{p}}}=\left(\frac{c^{2} \varepsilon_{0} m_{\mathrm{e}}}{n e^{2}}\right)^{1 / 2}=\left(\frac{m_{\mathrm{e}}}{\mu_{0} n e^{2}}\right)^{1 / 2}.\tag{7.43}\]

Pero este es solo un caso particular (para\(\ q=e\),\(\ m=m_{\mathrm{e}}\), y\(\ \mu=\mu_{0}\)) de la expresión (6.44), que se derivó en la Sec. 6.4 para la profundidad de la penetración del campo magnético en un conductor sin pérdidas (libre de colisión) en la aproximación cuasistática. Este hecho demuestra nuevamente que, como ya se discutió en la Sec. 6.7, esta aproximación (en la que se descuidan las corrientes de desplazamiento) da una descripción adecuada de los fenómenos dependientes del tiempo en\(\ \omega<<\omega_{\mathrm{p}}\), es decir, at\(\ \delta<<c / \omega=1 / k=\lambda / 2 \pi\). ¹⁸

Hay dos ejemplos más importantes de plasmas naturales. Para la ionosfera de la Tierra, es decir, la parte superior de su atmósfera, que está casi completamente ionizada por los componentes ultravioleta y de rayos X de la radiación del Sol, el valor máximo de\(\ n\), alcanzado unos 300 km sobre la superficie de la Tierra, está entre\(\ 10^{10}\) y\(\ 10^{12} \mathrm{~m}^{-3}\) (dependiendo del tiempo del día y la fase de actividad del Sol), de manera que la frecuencia plasmática máxima (37) esté entre 1 y 10 MHz. Esto es mucho mayor que el tiempo típico de colisión recíproca de las partículas,\(\ \tau^{-1}\) por lo que la Ec. (38) da una buena descripción de la dispersión de ondas en este plasma. El efecto de la reflexión de las ondas\(\ \omega<\omega_{\mathrm{p}}\) desde la ionosfera permite las comunicaciones de radio de largo alcance (sobre el globo) y la difusión en las llamadas ondas cortas, con frecuencias cíclicas del orden de 10 MHz: ¹⁹ pueden propagarse en el canal plano formado por el La superficie de la Tierra y la ionosfera, siendo reflejadas repetidamente por estas “paredes” paralelas. Desafortunadamente, debido a las variaciones aleatorias de la actividad de Sun, y por lo tanto de\(\ \omega_{\mathrm{p}}\), este canal natural de radiocomunicación no es demasiado confiable, y en nuestra era de cables transmundiales de fibra óptica (ver Sec. 7 abajo), su importancia práctica ha disminuido.

Otro ejemplo importante de plasmas son los electrones libres en metales y otros conductores. Para un metal típico,\(\ n\) es del orden de\(\ 10^{23} \mathrm{~cm}^{-3} \equiv 10^{29} \mathrm{~m}^{-3}\), por lo que la Ec. (37) rinde\(\ \omega_{\mathrm{p}} \sim 10^{16} \mathrm{~s}^{-1}\). Dicho valor de\(\ \omega_{\mathrm{p}}\) es algo mayor que las frecuencias ópticas medias\(\ \left(\omega \sim 3 \times 10^{15} \mathrm{~s}^{-1}\right)\). Esto explica por qué las superficies metálicas planas y limpias, como las películas de aluminio y plata utilizadas en los espejos, son tan brillantes: a estas frecuencias su permitividad compleja\(\ \varepsilon(\omega)\) es casi exactamente real y negativa, lo que lleva a la reflexión de la luz, con muy poca absorción.

El modelo simple (36), que descuida la dispersión de electrones, se vuelve inadecuado a frecuencias más bajas,\(\ \omega \tau \sim 1\). Una buena manera fenomenológica de extender el modelo a la cuenta de dispersión es tomar, en la Ec. (33), que la frecuencia más baja sea igual\(\ \omega_{j}\) a cero (para describir los electrones libres), manteniendo el coeficiente de amortiguamiento\(\ \delta_{0}\) de este modo mayor que cero, para dar cuenta de su disipación de energía debida a la dispersión. Luego, la Ec. (33) se reduce a

\[\ \varepsilon_{\mathrm{ef}}(\omega)=\varepsilon_{\mathrm{opt}}(\omega)+\frac{n_{0} q^{2}}{m} \frac{1}{-\omega^{2}-2 i \omega \delta_{0}} \equiv \varepsilon_{\mathrm{opt}}(\omega)+i \frac{n_{0} q^{2}}{2 \delta_{0} m \omega} \frac{1}{1-i \omega / 2 \delta_{0}},\tag{7.44}\]

donde la respuesta\(\ \varepsilon_{\mathrm{opt}}(\omega)\) a frecuencias altas (en la práctica, ópticas) sigue siendo dada por la Ec. (33), pero ahora con\(\ j>0\). El resultado (44) permite una interpretación sencilla. Para demostrarlo, incorporemos a nuestros cálculos la conducción óhmica del medio, generalizando la Ec. (4.7) como para\(\ \mathbf{j}_{\omega}=\sigma(\omega) \mathbf{E}_{\omega}\) dar cuenta de la posible dependencia de frecuencia de la conductividad óhmica. Conectando esta relación a la imagen de Fourier de la ecuación macroscópica relevante de Maxwell\(\ \nabla \times \mathbf{H}_{\omega}=\mathbf{j}_{\omega}-i \omega \mathbf{D}_{\omega} \equiv \mathbf{j}_{\omega}-i \omega \varepsilon(\omega) \mathbf{E}_{\omega}\),, obtenemos

\[\ \nabla \times \mathbf{H}_{\omega}=[\sigma(\omega)-i \omega \varepsilon(\omega)] \mathbf{E}_{\omega}.\tag{7.45}\]

Esta relación muestra que para una onda monocromática, la adición de la densidad de corriente óhmica\(\ \mathbf{j}_{\omega}\) a la densidad de corriente de desplazamiento es equivalente a la adición de\(\ \sigma(\omega)\) a\(\ -i \omega \varepsilon(\omega)\), es decir, al siguiente cambio de la permitividad eléctrica ac: ²⁰

\[\ \varepsilon(\omega) \rightarrow \varepsilon_{\mathrm{ef}}(\omega) \equiv \varepsilon_{\mathrm{opt}}(\omega)+i \frac{\sigma(\omega)}{\omega}.\tag{7.46}\]

Ahora la comparación de las ecuaciones (44) y (46) muestra que coinciden si tomamos

\[\ \sigma(\omega)=\frac{n_{0} q^{2} \tau}{m_{0}} \frac{1}{1-i \omega \tau} \equiv \sigma(0) \frac{1}{1-i \omega \tau},\quad\quad\quad\quad\text{Generalized Drude formula}\tag{7.47}\]

donde la conductividad dc\(\ \sigma(0)\) es descrita por la fórmula Drude (4.13), y el coeficiente fenomenológicamente introducido\(\ \delta_{0}\) se asocia con\(\ 1 / 2 \tau\). Eq. (47), que frecuentemente se llama la fórmula Drude generalizada (o “ac”, o “rf”), ²¹ da una descripción muy razonable (semicuantitativa) de la conductividad ac de muchos metales casi hasta frecuencias ópticas.

Volviendo ahora a nuestra discusión sobre el modelo generalizado de Lorentz (33), vemos que las dependencias de frecuencia de las\(\ \left(\varepsilon^{\prime \prime}\right)\) partes real\(\ \left(\varepsilon^{\prime}\right)\) e imaginaria de la permitividad compleja que produce no son del todo independientes. Por ejemplo, echemos una mirada más a los picos de resonancia en la Fig. 5. Cada vez que la parte real cae con frecuencia,\(\ d \varepsilon^{\prime} / d \omega<0\), su parte imaginaria\(\ \varepsilon^{\prime \prime}\) tiene un pico positivo. Ralph Kronig (en 1926) y Hendrik (“Hans”) Kramers (en 1927) demostraron independientemente que esto no es una coincidencia ocasional pertinente sólo para este modelo en particular. Además, el pleno conocimiento de la función\(\ \varepsilon^{\prime}(\omega)\) permite el cálculo de la función\(\ \varepsilon^{\prime \prime}(\omega)\), y viceversa. La razón matemática de este hecho es que ambas funciones están siempre relacionadas con una sola función real\(\ G(\theta)\) por las ecuaciones (27).

Para derivar las relaciones Kramers-Kronig, consideremos la Ec. (26b) en el plano de frecuencias complejas\(\ \omega \rightarrow \mathbf{\omega} \equiv \omega^{\prime}+i \omega^{\prime \prime}\):

\[\ f(\boldsymbol{\omega}) \equiv \varepsilon(\boldsymbol{\omega})-\varepsilon_{0}=\int_{0}^{\infty} G(\theta) e^{i \boldsymbol{\omega} \theta} d \theta \equiv \int_{0}^{\infty} G(\theta) e^{i \omega^{\prime} \theta} e^{-\omega^{\prime \prime} \theta} d \theta.\tag{7.48}\]

Para todos los sistemas físicos estables,\(\ G(\theta)\) tiene que ser finito para todos los valores importantes de la variable de integración real\(\ (\theta>0)\), y tienden a cero en\(\ \theta \rightarrow 0\) y\(\ \theta \rightarrow \infty\). (En efecto, según la Ec. (23), un distinto de cero\(\ G(0)\) significaría una respuesta instantánea del medio a la fuerza externa, mientras que\(\ G(\infty) \neq 0\) significaría que tiene una memoria infinitamente larga.) Por eso, y gracias al factor\(\ e^{-\omega^{\prime \prime} \theta}\), la expresión
bajo la integral en la ecuación (48) tiende a cero\(\ |\omega| \rightarrow \infty\) en todo el medio plano superior\(\ \left(\omega^{\prime \prime} \geq 0\right)\). En consecuencia,
podemos afirmar que la función compleja que\(\ f(\omega)\) da esta relación, es analítica en ese semiplano. Este hecho nos permite aplicarle la fórmula integral general de Cauchy ²²

\[\ f(\boldsymbol{\omega})=\frac{1}{2 \pi i} \oint_{C} f(\boldsymbol{\Omega}) \frac{d \boldsymbol{\Omega}}{\boldsymbol{\Omega}-\boldsymbol{\omega}},\tag{7.49}\]

donde también\(\ \boldsymbol{\Omega} \equiv \Omega^{\prime}+i \Omega^{\prime \prime}\) es una variable compleja. Tomemos el contorno\(\ C\) de integración de la forma mostrada en la Fig. 7, con el radio\(\ R\) del semicírculo mayor tendiendo al infinito, y el radio\(\ r\) del semicírculo más pequeño (alrededor del punto singular\(\ \boldsymbol{\Omega}=\omega\)) tendiendo a cero. Debido a la decadencia exponencial de\(\ |f(\boldsymbol{\Omega})|\) at\(\ |\boldsymbol{\Omega}| \rightarrow \infty\), la contribución al lado derecho de la ecuación (49) del semicírculo más grande desaparece, ²³ mientras que la contribución del semicírculo pequeño, donde\(\ \boldsymbol{\Omega}=\omega+r \exp \{i \varphi\}\), con\(\ -\pi \leq \varphi \leq 0\), es

\[\ \lim _{r \rightarrow 0} \frac{1}{2 \pi i} \int_{\boldsymbol{\Omega}=\omega+r \exp \{i \varphi)} f(\boldsymbol{\Omega}) \frac{d \boldsymbol{\Omega}}{\boldsymbol{\Omega}-\omega}=\frac{f(\omega)}{2 \pi i} \int_{-\pi}^{0} \frac{i r \exp \{i \varphi\} d \varphi}{r \exp \{i \varphi\}} \equiv \frac{f(\omega)}{2 \pi} \int_{-\pi}^{0} d \varphi=\frac{1}{2} f(\omega).\tag{7.50}\]

Fig. 7.7. Derivando las relaciones de dispersión Kramers-Kronig.

Como resultado, para nuestro contorno\(\ C\), la Eq. (49) rinde

\[\ f(\omega)=\lim _{r \rightarrow 0} \frac{1}{2 \pi i}\left(\int_{-\infty}^{\omega-r}+\int_{\omega+r}^{+\infty}\right) f(\Omega) \frac{d \Omega}{\Omega-\omega}+\frac{1}{2} f(\omega).,\tag{7.51}\]

donde\(\ \Omega \equiv \Omega^{\prime}\) en el eje real (donde\(\ \Omega^{\prime \prime}=0\)). Tal integral, excluyendo una vecindad infinitesimal simétrica de una singularidad polar, se denomina el valor principal de la integral (formalmente, divergente) de\(\ -\infty\) a\(\ +\infty\), y se denota con la letra P anterior a ella. ²⁴ Usando esta notación, restando\(\ f(\omega) / 2\) de ambas partes de la Eq. (51), y multiplicándolas por 2, obtenemos

\[\ f(\omega)=\frac{1}{\pi i} \mathrm{P} \int_{-\infty}^{+\infty} f(\Omega) \frac{d \Omega}{\Omega-\omega}.\tag{7.52}\]

Ahora enchufando a esta compleja igualdad la diferencia relacionada con la polarización\(\ f(\omega) \equiv \varepsilon(\omega)-\varepsilon_{0}\) en la forma\(\ \left[\varepsilon^{\prime}(\omega)-\varepsilon_{0}\right]+i\left[\varepsilon^{\prime \prime}(\omega)\right]\), y requiriendo que tanto los componentes reales como los imaginarios de los dos lados de la ecuación (52) sean iguales por separado, obtenemos las famosas relaciones de dispersión Kramers-Kronig

\[\ \text{Kramers-Kronig dispersion relations}\quad\quad\quad\quad\varepsilon^{\prime}(\omega)=\varepsilon_{0}+\frac{1}{\pi} \mathrm{P} \int_{-\infty}^{+\infty} \varepsilon^{\prime \prime}(\Omega) \frac{d \Omega}{\Omega-\omega}, \quad \varepsilon^{\prime \prime}(\omega)=-\frac{1}{\pi} \mathrm{P} \int_{-\infty}^{+\infty}\left[\varepsilon^{\prime}(\Omega)-\varepsilon_{0}\right] \frac{d \Omega}{\Omega-\omega}.\tag{7.53}\]

Podemos usar el hecho ya mencionado que siempre\(\ \varepsilon^{\prime}(\omega)\) es una función par, mientras que\(\ \varepsilon^{\prime \prime}(\omega)\) una
función impar de frecuencia, para reescribir estas relaciones en la siguiente forma equivalente,

\[\ \varepsilon^{\prime}(\omega)=\varepsilon_{0}+\frac{2}{\pi} \mathrm{P} \int_{0}^{+\infty} \varepsilon^{\prime \prime}(\Omega) \frac{\Omega d \Omega}{\Omega^{2}-\omega^{2}}, \quad \varepsilon^{\prime \prime}(\omega)=-\frac{2 \omega}{\pi} \mathrm{P} \int_{0}^{+\infty}\left[\varepsilon^{\prime}(\Omega)-\varepsilon_{0}\right] \frac{d \Omega}{\Omega^{2}-\omega^{2}},\tag{7.54}\]

lo cual es más conveniente para la mayoría de las aplicaciones, ya que involucra solo frecuencias físicas (positivas).

Aunque las relaciones Kramers-Kronig son “globales” en frecuencia, en ciertos casos permiten un cálculo aproximado de la dispersión a partir de datos experimentales para absorción, recopilados incluso dentro de un rango de frecuencia limitado (“local”). Lo más importante es que si un medio tiene un pico de absorción agudo a alguna frecuencia\(\ \omega_{j}\), podemos describirlo como

\[\ \varepsilon^{\prime \prime}(\omega) \approx c \delta\left(\omega-\omega_{j}\right)+\text { a more smooth function of } \omega,\tag{7.55}\]

y el primero de Eqs. (54) inmediatamente da

\[\ \varepsilon^{\prime}(\omega) \approx \varepsilon_{0}+\frac{2 c}{\pi} \frac{\omega_{j}}{\omega_{j}^{2}-\omega^{2}}+\text { another smooth function of } \omega\quad\quad\quad\quad\text{Dispersion near an absorption line}\tag{7.56}\]

prediciendo así la dispersión anómala cerca de tal punto. Este cálculo muestra que dicho comportamiento observado en el modelo del oscilador Lorentz (ver Fig. 5) no es de ninguna manera ocasional o específico del modelo.

Permítanme recalcar nuevamente que las relaciones Kramers-Kronig (53) - (54) son mucho más generales que el modelo de Lorentz (33), y solo requieren una relación causal, lineal (21) entre la polarización\(\ P(t)\) con el campo eléctrico\(\ E\left(t^{\prime}\right)\). ²⁵ Por lo tanto, estas relaciones también son válidas para las funciones complejas que relacionan imágenes de Fourier de cualquier par de variables relacionadas con causa/efecto. En particular, a una medida de cualquier respuesta lineal\(\ r(t)\) de cualquier muestra experimental a cualquier campo externo\(\ f\left(t^{\prime}\right)\), cualquiera que sea la naturaleza de esta respuesta y la física detrás de ella, podemos estar seguros de que existe una relación causal entre las variables\(\ r\) y\(\ f\), de manera que el función compleja correspondiente\(\ \chi(\omega) \equiv r_{\omega} / f_{\omega}\) sí obedece las relaciones Kramers-Kronig. Sin embargo, es importante recordar que una relación lineal entre las amplitudes de Fourier de dos variables no implica necesariamente una relación causal entre ellas. ²⁶

---

Referencia

⁸ En un medio isotrópico, los vectores E, P, y por lo tanto\(\ \mathbf{D}=\varepsilon_{0} \mathbf{E}+\mathbf{P}\), son todos paralelos, y para la simplicidad de la notación,
dejaré caer el signo vectorial en las siguientes fórmulas. También estoy asumiendo que P en cualquier punto r sólo depende del campo eléctrico en el mismo punto, y de ahí bajar el factor\(\ \exp \{i k z\}\), lo mismo para todas las variables. Esta última suposición es válida si la longitud de onda\(\ \lambda\) es mucho mayor que el tamaño del dipolo medio elemental\(\ a\). En la mayoría de los sistemas de interés, la escala de\(\ a\) es atómica\(\ \left(\sim 10^{-10} \mathrm{~m}\right)\), por lo que la aproximación es válida hasta frecuencias muy altas\(\ \omega \sim c / a \sim 10^{18} \mathrm{~s}^{-1}\),, correspondientes a rayos X duros.

⁹ La idea de estas funciones es muy similar a la de las funciones espaciales del Green (ver Sec. 2.10), pero con el nuevo giro, debido al principio de causalidad. Una discusión sobre las funciones temporales del Green en aplicación a la mecánica clásica (que en cierta medida se solapa con nuestra discusión actual) se puede encontrar en CM Sec. 5.1.

¹⁰ Las primeras observaciones inequívocas de dispersión (para el caso de la refracción de la luz) fueron descritas por Sir Isaac Newton en su Óptica (1704) — ¡aunque este genio nunca ha reconocido la naturaleza ondulada de la luz!

¹¹ Puede ser tentador atribuir este efecto a la absorción de la onda, es decir, la disipación de la energía de la ola, pero veremos muy pronto que la atenuación de la onda también puede deberse a diferentes efectos.

¹² El lector probablemente esté familiarizado con el efecto más notable de la dispersión: la diferencia entre la velocidad de ese grupo\(\ \nu_{\mathrm{gr}} \equiv d \omega / d k^{\prime}\), dando la velocidad de la envolvente de un paquete de ondas con un espectro de frecuencia estrecho, y la velocidad\(\ \nu _{\mathrm{ph}} \equiv \omega / k^{\prime}\) de fase de las ondas componentes. El efecto de dispersión de segundo orden, proporcional a\(\ d^{2} \omega / d^{2} k^{\prime}\), conduce a la deformación (ensanchamiento gradual) de la envoltura misma. Siguiendo la tradición, estos efectos se discuten con más detalle en la parte de mecánica cuántica de esta serie (QM Sec. 2.2), porque son el factor crucial de la mecánica de olas de Schrödinger. (Véase también una breve discusión en CM Sec. 6.3.)

¹³ Este ejemplo se centra en la dependencia de frecuencia de\(\ varepsilon\) más que\(\ \mu\), porque las ondas electromagnéticas interactúan con los medios “habituales” a través de su campo eléctrico mucho más que a través del campo magnético. En efecto, según la Ecuación (7), el campo magnético de la onda es del orden de\(\ E / c\), de manera que el componente magnético de la fuerza de Lorentz (5.10), actuando sobre una partícula no relativista\(\ F_{\mathrm{m}} \sim q u B \sim(u / c) q E\), es mucho menor que el de su componente eléctrico,\(\ F_{\mathrm{e}}=q E\), y puede ser descuidado. Sin embargo, como se discutirá en la Sec. 6, olvidarse de la posible dispersión de\(\ \mu(\omega)\) puede resultar en perder algunas oportunidades notables para manipular las olas.

¹⁴ Si este punto no es del todo claro, favor de ver CM Sec. 5.1 para una discusión más detallada.

¹⁵ En óptica, dicho comportamiento se denomina dispersión anómala.

¹⁶ Véase, por ejemplo, QM Capítulos 5-6.

¹⁷ Para una onda plana arbitraria, el flujo de potencia promedio total puede calcularse como una integral de la ecuación (42) en todas las frecuencias. Por cierto, combinando esta integral y el teorema de Poynting (6.111), es sencillo probar la siguiente expresión interesante para la densidad de energía electromagnética promedio de un paquete de\(\ (\Delta \omega<<\omega)\) onda estrecha que se propaga en un medio dispersivo arbitrario (pero lineal e isotrópico):

\(\ \bar{u}=\frac{1}{2} \int_{\text {packet }}\left\{\frac{d\left[\omega \varepsilon^{\prime}(\omega)\right]}{d \omega} E_{\omega} E_{\omega}^{*}+\frac{d\left[\omega \mu^{\prime}(\omega)\right]}{d \omega} H_{\omega} H_{\omega}^{*}\right\} d \omega .\)

¹⁸ Una conveniencia más del modelo simple de un plasma libre de colisiones, que nos ha llevado a la ecuación (36), es que puede generalizarse fácilmente al caso de un campo magnético adicional de CC fuerte\(\ \mathbf{B}_{0}\) (mucho mayor que el de la onda) aplicado en la dirección n de onda propagación. Es sencillo (y por lo tanto dejado para el lector) demostrar que dicho plasma exhibe el efecto Faraday de la rotación del plano de polarización, y por lo tanto da un ejemplo de un medio anisotrópico que viola la relación de reciprocidad de Lorentz (6.121).

¹⁹ Estas frecuencias son un orden de magnitud inferiores a las utilizadas para la radiodifusión televisiva y FM.

²⁰ Alternativamente, de acuerdo con la Ec. (45), es posible (y en el campo de la espectroscopia infrarroja, convencional) atribuir la respuesta ac de un medio en todas las frecuencias a su conductividad compleja efectiva:\(\ \sigma_{\mathrm{ef}}(\omega)\equiv\sigma(\omega)-i \omega \varepsilon(\omega) \equiv-i \omega \varepsilon_{\mathrm{ef}}(\omega)\).

²¹ También puede derivarse de la ecuación cinética de Boltzmann en la llamada aproximación de relajación-tiempo (RTA) — véase, por ejemplo, SM Sec. 6.2.

²² Véase, por ejemplo, MA Ec. (15.2).

²³ Estrictamente hablando, esto también requiere\(\ |f(\Omega)|\) disminuir más rápido que\(\ \Omega^{-1}\) en el eje real (at\(\ \Omega^{\prime \prime}=0\)), pero debido a la
inercia de las partículas cargadas, este requisito se cumple para todos los modelos realistas de dispersión — véase, por ejemplo, la Ec. (36).

²⁴ Estoy escribiendo este símbolo en una fuente romana (vertical), para evitar cualquier posibilidad de su confusión con la polarización del medio.

²⁵ En realidad, en matemáticas, las relaciones incluso algo más generales que las ecuaciones (53), válidas para una función analítica arbitraria de argumento complejo, se conocen al menos a partir de 1868 (el teorema de Sokhotski-Plemelj).

²⁶ Por ejemplo, la función\(\ \varphi(\omega) \equiv E_{\omega} / P_{\omega}\), en el modelo del oscilador Lorentz, no obedece a las relaciones Kramers-Kronig. Esto es evidente no sólo físicamente, por el hecho de que no\(\ E(t)\) es una función causal de\(\ P(t)\), sino incluso matemáticamente. De hecho, la función de Green que describe una relación causal tiene que tender a cero en pequeños retrasos de tiempo\(\ \theta \equiv t-t^{\prime}\), de modo que su imagen de Fourier tiene que tender a cero en\(\ \omega \rightarrow \pm \infty\). Esto es ciertamente cierto para la función\(\ f(\omega)\) dada por la ecuación (32), pero no para la función recíproca\(\ \varphi(\omega) \equiv 1 / f(\omega) \propto\left(\omega^{2}-\omega_{0}^{2}\right)-2 i \delta \omega\), que diverge a grandes frecuencias.