7.8: Resonadores

Los resonadores son osciladores distribuidos, es decir, estructuras que pueden sostener ondas estacionarias (en electrodinámica, oscilaciones del campo electromagnético) incluso sin una fuente externa, hasta que la amplitud de oscilación disminuye lentamente en el tiempo debido a inevitables pérdidas de energía. Si la calidad del resonador (descrita por el llamado\(\ Q\) factor -que se definirá y discutirá en la siguiente sección) es alta\(\ Q>> 1\), esta decadencia toma muchos períodos de oscilación. Alternativamente,\(\ Q\) los resonadores altos pueden sostener campos oscilantes altos permanentemente, si son impulsados por ondas incidentes relativamente débiles.

Conceptualmente, el resonador más simple es el interferómetro ⁷⁹ de Fabry-Pérot que se puede obtener colocando dos planos bien conductores paralelos entre sí. ⁸⁰ Efectivamente, en la Sec. 3 hemos visto que si una onda plana incide normalmente sobre tal “espejo perfecto”, localizado en, su reflejo\(\ z = 0\), a una profundidad insignificante de la piel, da como resultado una onda estacionaria descrita por la Ec. (61b):

\[\ E(z, t)=\operatorname{Re}\left(2 E_{\omega} e^{-i \omega t+i \pi / 2}\right) \sin k z.\tag{7.195}\]

Esta onda no cambiaría si de repente hubiéramos puesto el segundo espejo (aislando el segmento de longitud\(\ l\) de la fuente de onda externa) en cualquier posición\(\ z=l\) con pecado\(\ k l=0\), es decir, con

\[\ k l=p \pi, \quad \text { where } p=1,2, \ldots.\tag{7.196}\]

Esta condición, que determina el espectro de frecuencias eigen (o propias, o de resonancia) del resonador de longitud fija\(\ l\),

\[\ \omega_{p}=\nu k_{p}=\frac{\pi \nu}{a} p, \quad \text { with } \nu=\frac{1}{(\varepsilon \mu)^{1 / 2}},\tag{7.197}\]

tiene un sentido físico simple: la longitud del resonador\(\ l\) equivale exactamente a\(\ p\) medias ondas de la frecuencia\(\ \omega_{p}\). Aunque todo esto es muy simple, por favor note un cambio considerable de filosofía con respecto a lo que hemos estado haciendo en las secciones anteriores: la tarea principal del análisis del resonador es encontrar sus frecuencias propias\(\ \omega_{p}\) que ahora están determinadas por la geometría del sistema y no por una fuente de onda externa.

Antes de pasar a resonadores más complejos, usemos la ecuación (62) para representar el campo magnético en el interferómetro de Fabry-Pérot:

\[\ H(z, t)=\operatorname{Re}\left(2 \frac{E_{\omega}}{Z} e^{-i \omega t}\right) \cos k z.\tag{7.198}\]

Las expresiones (195) y (198) muestran que a diferencia de las ondas viajeras, cada campo de la onda estacionaria cambia simultáneamente (proporcionalmente) en todos los puntos del resonador Fabry-Pérot, volviéndose a cero en todas partes dos veces por período. En estos instantes, la energía del campo correspondiente desaparece, pero la energía total de las oscilaciones permanece constante porque el campo homólogo oscila con el desplazamiento de fase\(\ \pi / 2\). Tal comportamiento es típico para todos los resonadores electromagnéticos.

Otra observación más técnica es que podemos obtener fácilmente los mismos resultados (195) - (198) resolviendo las ecuaciones de Maxwell desde cero. Por ejemplo, ya sabemos que en ausencia de dispersión, pérdidas y fuentes, se reducen a las ecuaciones de onda (3) para cualquier componente de campo. Para el análisis del resonador Fabry-Pérot, podemos usar la forma 1D de estas ecuaciones, digamos, para la componente transversal del campo eléctrico:

\[\ \left(\frac{\partial^{2}}{\partial z^{2}}-\frac{1}{\nu^{2}} \frac{\partial^{2}}{\partial t^{2}}\right) E=0,\tag{7.199}\]

y resolverlo como parte de un problema de valor propio con las condiciones de contorno correspondientes. En efecto, separando variables de tiempo y espacio como\(\ E(z, t)=Z(z) \mathcal{T}(t)\), obtenemos

\[\ \frac{1}{Z} \frac{d^{2} Z}{d z^{2}}-\frac{1}{\nu^{2}} \frac{1}{\mathcal{T}} \frac{d^{2} \mathcal{T}}{d t^{2}}=0.\tag{7.200}\]

Llamando a la constante de separación\(\ k^{2}\), obtenemos dos ecuaciones diferenciales ordinarias similares,

\[\ \frac{d^{2} Z}{d z^{2}}+k^{2} Z=0, \quad \frac{d^{2} \mathcal{T}}{d t^{2}}+k^{2} \nu^{2} \mathcal{T}=0,\tag{7.201}\]

ambas con soluciones sinusoidales, de manera que el producto\(\ Z(z) \mathcal{T}(t)\) es una onda estacionaria con el vector de onda\(\ k\) y la frecuencia\(\ \omega=k \nu\). (De esta forma, las ecuaciones son válidas incluso en presencia de dispersión, pero con una velocidad de onda dependiente de la frecuencia:\(\ \nu^{2}=1 / \varepsilon(\omega) \mu(\omega)\).) Ahora usando las condiciones de límite\(\ E(0, t)=E(l, t)=0\), ⁸¹ obtenemos el espectro de valores propios para\(\ k_{p}\) y por lo tanto para\(\ \omega_{p}=\nu k_{p}\), dado por las ecuaciones. (196) y (197).

Las lecciones de este simple estudio de caso pueden generalizarse fácilmente para un resonador arbitrario: existen (al menos: -) dos enfoques para encontrar el espectro de frecuencias propias:

(i) Podemos ver una solución de ondas viajeras y encontrar dónde pueden insertarse espejos reflectantes sin afectar la estructura de la ola. Desafortunadamente, este método se limita a geometrías simples.

(ii) Podemos resolver las ecuaciones generales de onda 3D,

\[\ \left(\nabla^{2}-\frac{1}{\nu^{2}} \frac{\partial^{2}}{\partial t^{2}}\right) f(\mathbf{r}, t)=0,\tag{7.202}\]

para componentes de campo, como un problema de valor propio con condiciones de contorno adecuadas. Si los parámetros del sistema (y por lo tanto el coeficiente\(\ \nu\)) no cambian en el tiempo, las variables espaciales y temporales de la ecuación (202) siempre pueden separarse tomando

\[\ f(\mathbf{r}, t)=\mathcal{R}(\mathbf{r}) \mathcal{T}(t),\tag{7.203}\]

donde la función\(\ \mathcal{T}(t)\) siempre obedece a la misma ecuación que en la Ec. (201), teniendo la solución sinusoidal de frecuencia\(\ \omega=\nu k\). Volviendo a conectar esta solución a las ecuaciones (202), para la distribución espacial del campo, obtenemos la ecuación 3D de Helmholtz,

\[\ \left(\nabla^{2}+k^{2}\right) \mathcal{R}(\mathbf{r})=0,\quad\quad\quad\quad \text{3D Helmholtz equation}\tag{7.204}\]

cuya solución (para geometrías no simétricas) puede ser mucho más compleja.

Usemos estos enfoques para encontrar el espectro de frecuencias propias de unos pocos resonadores simples, pero prácticamente importantes. En primer lugar, el primer método es completamente suficiente para el análisis de cualquier resonador formado como un fragmento de una línea de transmisión TEM uniforme (por ejemplo, un cable coaxial), confinado con dos tapas conductoras normales a la dirección de la línea. En efecto, dado que en tales líneas\(\ k_{z}=k=\omega / \nu\), y el campo eléctrico es perpendicular al eje de propagación, por ejemplo, paralelo a la superficie de la tapa, las condiciones límite son exactamente las mismas que en el resonador Fabry-Pérot, y volvemos a llegar al espectro de frecuencias propias (197).

Ahora analicemos un sistema un poco más complejo: una cavidad rectangular de pared metálica de volumen\(\ a \times b \times l\)

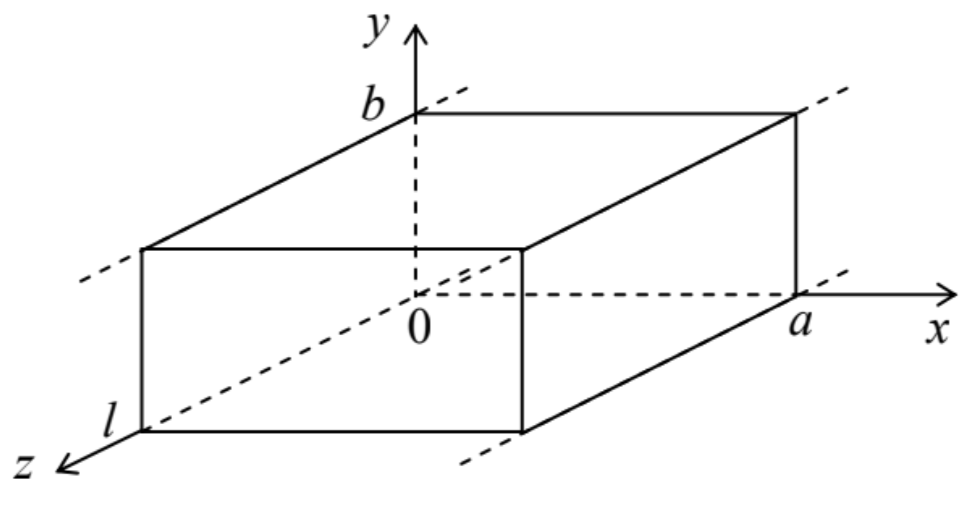Fig. 7.29. Resonador rectangular de pared metálica como sección finita de una guía de ondas con la sección transversal mostrada en la figura 22.

Para utilizar el primer enfoque descrito anteriormente, consideremos el resonador como una\(\ (\Delta \mathrm{z}=l)\) sección de longitud finita de la guía de ondas rectangular estirada a lo largo del eje\(\ z\), lo cual fue analizado en detalle en la Sec. 6. Como recordatorio, at\(\ a<b\), en el modo fundamental de onda\(\ H_{10}\) viajera, ambos vectores E y H no dependen de y, teniendo E solo un componente y. En contraste, H tiene dos componentes,\(\ H_{x}\) y\(\ H_{z}\), con el desplazamiento de fase\(\ \pi / 2\) entre ellos, y con\(\ H_{x}\) tener la misma fase que\(\ E_{y}\) — ver las ecuaciones (131), (137) y (138). De ahí que si se coloca un plano perpendicular al eje z, de manera que el campo eléctrico se desvanece sobre él,\(\ H_{x}\) también se
desvanece, de manera que ambas condiciones límite (104), pertinentes a una pared metálica perfecta, se cumplen simultáneamente.

Como resultado, la\(\ H_{10}\) onda no sería perturbada por dos paredes metálicas separadas por un número entero de medias longitudes de onda\(\ \lambda_{z} / 2\) correspondientes al número de onda dado por la combinación de las ecuaciones (102) y (133):

\[\ k_{z}=\left(k^{2}-k_{t}^{2}\right)^{1 / 2}=\left(\frac{\omega^{2}}{\nu^{2}}-\frac{\pi^{2}}{a^{2}}\right).\tag{7.205}\]

Usando esta expresión, vemos que la menor de estas distancias,\(\ l=\lambda_{\mathrm{z}} / 2=\pi / k_{\mathrm{z}}\), da la frecuencia de resonancia ⁸²

\[\ \omega_{101}=\nu\left[\left(\frac{\pi}{a}\right)^{2}+\left(\frac{\pi}{l}\right)^{2}\right]^{1 / 2},\tag{7.206}\]

donde los índices de\(\ \omega\) muestran los números de medias ondas a lo largo de cada dimensión del sistema, en el orden\(\ [a, b, l]\). Esta es la frecuencia propia más baja (fundamental) del resonador (si\(\ b<a, l\)).

La distribución de campo en este modo es cercana a la del modo de guía de ondas correspondiente\(\ H_{10}\) (Fig. 22), con la importante diferencia de que los campos magnético y eléctrico están ahora desplazados por fase\(\ \pi / 2\) tanto en el espacio como en el tiempo, al igual que en el resonador Fabry-Pérot — ver Ecuaciones (195) y (198). Tal cambio de tiempo permite una interpretación muy simple del\(\ H_{101}\) modo, que es especialmente adecuado para resonadores muy planos, con\(\ b<<a, l\). En el instante en que el campo eléctrico alcanza su máximo (Fig. 30a), es decir, cuando el campo magnético se desvanece en todo el volumen, la carga eléctrica superficial de las paredes (con la densidad de área\(\ \sigma=E_{n} / \varepsilon\)) es mayor, localizándose principalmente en el medio de las caras más amplias (en la Fig. 30, horizontales) de la resonador. En los momentos posteriores inmediatos, las paredes comienzan a recargarse a través de corrientes superficiales, cuya densidad\(\ J\) es mayor en las paredes laterales, y alcanza su valor máximo en una cuarta parte del período de oscilación\(\ \mathcal{T}=2 \pi / \omega_{101}\) — ver Fig. 30b.

Fig. 7.30. Campos, cargas y corrientes en el\(\ \left(H_{101}\right)\) modo fundamental de un resonador metálico rectangular, en dos instantes separados por\(\ \Delta t=\pi / 2 \omega_{101}\) — esquemáticamente.

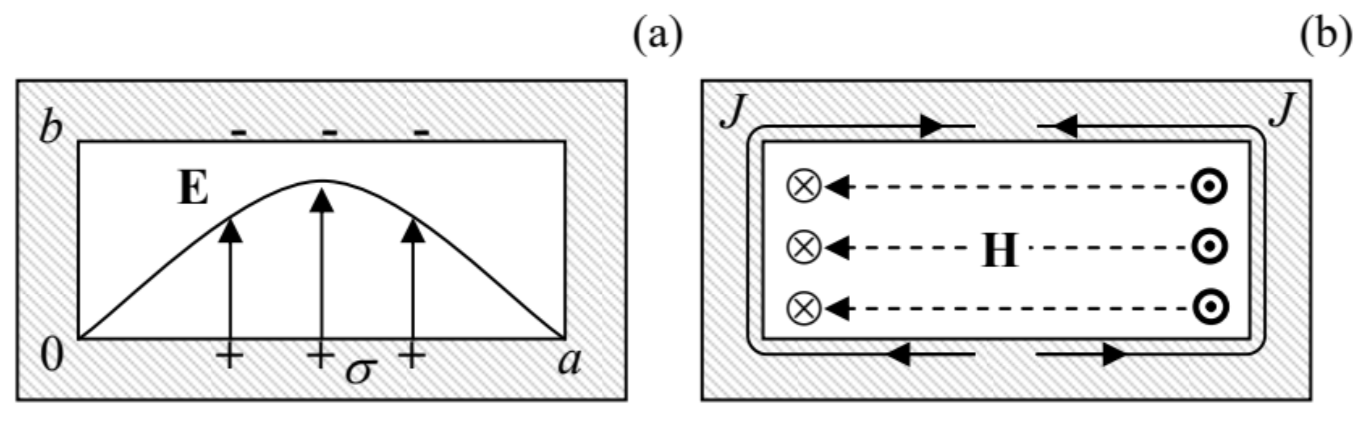
Las corrientes generan el campo magnético vórtice, con líneas de campo en bucle en el plano de la cara más amplia del resonador. Las corrientes superficiales continúan fluyendo en esta dirección hasta que (en un cuarto de periodo más) las paredes más anchas del resonador se recargan completamente en la polaridad opuesta a la mostrada en la Fig. 30a. Después de eso, las corrientes superficiales comienzan a fluir en dirección opuesta a la mostrada en la Fig. 30b. Este proceso, que se repite una y otra vez, es conceptualmente similar a las conocidas oscilaciones en un\(\ LC\) circuito agrupado, con el papel de capacitancia (ahora, distribuida) desempeñada principalmente por las caras más amplias del resonador, y la de inductancia (ahora, distribuida), por sus paredes más estrechas.

Para generalizar el resultado (206) a modos de oscilación más altos, el segundo de los enfoques discutidos anteriormente es más prudente. Separando las variables en la ecuación de Helmholtz (204) como\(\ \mathcal{R}(\mathbf{r})=X(x)Y(y)Z(z)\), vemos eso\(\ X\),\(\ Y\), y\(\ Z\) tienen que ser funciones sinusoidales o cosinusoidales de sus argumentos, con componentes de vector de onda que satisfacen la ecuación característica

\[\ k_{x}^{2}+k_{y}^{2}+k_{z}^{2}=k^{2} \equiv \frac{\omega^{2}}{\nu^{2}}\tag{7.207}\]

En contraste con el problema de propagación de ondas, ahora estamos tratando con ondas estacionarias a lo largo de las tres dimensiones, y tenemos que satisfacer las condiciones de límite macroscópicas (104) en todos los conjuntos de paredes paralelas. Es sencillo verificar que estas condiciones\(\ \left(E_{\tau}=0, H_{n}=0\right)\) se cumplan en la siguiente distribución de componentes de campo:

\ [\\ comenzar {array} {ll}
E_ {x} =E_ {1}\ cos k_ {x} x\ sin k_ {y} y\ sin k_ {z} z, & H_ {x} =H_ {1}\ sin k_ {x} x\ cos k_ {y} y\ cos k_ {z} z,\\
E_ {y} =E_ {2}\ sin k_ {x} x\ cos k_ {y} y\ sin k_ {z} z, & H_ {y} =H_ {2}\ cos k_ {x} x\ sin k_ {y} y\ cos k_ {z} z,\\
E_ {z} =E_ {3}\ sin k_ {x } x\ sin k_ {y} y\ cos k_ {z} z, & H_ {z} =H_ {3}\ cos k_ {x} x\ cos k_ {y} y\ sin k_ {z} z,
\ end {array}\ tag {7.208}\]

teniendo cada uno de los componentes del vector de onda un espectro equidistante, similar a la Ec. (196):

\[\ k_{x}=\frac{\pi n}{a}, \quad k_{y}=\frac{\pi m}{b}, \quad k_{z}=\frac{\pi p}{l},\tag{7.209}\]

de manera que el espectro completo de frecuencias propias viene dado por la siguiente fórmula,

\[\ \omega_{n m p}=\nu k=\nu\left[\left(\frac{\pi n}{a}\right)^{2}+\left(\frac{\pi m}{b}\right)^{2}+\left(\frac{\pi p}{l}\right)^{2}\right]^{1 / 2},\tag{7.210}\]

que es una generalización natural de la Ec. (206). Tenga en cuenta, sin embargo, el de los tres enteros\(\ m\)\(\ n\), y\(\ p\), al menos dos tienen que ser diferentes de cero para evitar que los campos (208) se desvanezcan en todos los puntos.

Podemos usar la ecuación (210), en particular, para evaluar el número de modos diferentes en un rango relativamente pequeño\(\ d^{3} k<<k^{3}\) del espacio del vector de onda, que es, por otro lado, mucho mayor que el volumen recíproco\(\ 1 / V=1 / a b l\),, del resonador. Teniendo en cuenta que cada frecuencia propia (210), con\(\ nml \neq 0\), corresponde a dos modos de campo con diferentes polarizaciones, ⁸³ la argumentación absolutamente similar a la utilizada para el caso 2D al final de la Sec. 7, arroja

\[\ \text{Oscillation mode density}\quad\quad\quad\quad d N=2 V \frac{d^{3} k}{(2 \pi)^{3}}.\tag{7.211}\]

Esta propiedad, válida para resonadores de forma arbitraria, es ampliamente utilizada en la física estadística clásica y cuántica, ⁸⁴ en la siguiente forma. Si algún modo electromagnético funcional\(\ f(\mathbf{k})\) es una función suave del vector de onda k, y el volumen\(\ V\) es lo suficientemente grande, entonces la ecuación (211) puede usarse para aproximar la
suma de los valores de la función sobre los modos mediante una integral:

\[\ \sum_{\mathbf{k}} f(\mathbf{k}) \approx \int_{N} f(\mathbf{k}) d N \equiv \int_{\mathbf{k}} f(\mathbf{k}) \frac{d N}{d^{3} k} d^{3} k=2 \frac{V}{(2 \pi)^{3}} \int_{\mathbf{k}} f(\mathbf{k}) d^{3} k.\tag{7.212}\]

Dejando análisis similares de cavidades resonantes de otras formas para el ejercicio del lector, permítanme terminar esta sección señalando que los resonadores de baja pérdida también pueden estar formados por secciones de longitud finita no solo de guías de onda de pared metálica de varias secciones transversales, sino también de las guías de ondas dieléctricas. Además, incluso una simple losa de un material dieléctrico con una\(\ \mu / \varepsilon\) relación sustancialmente diferente a la de su entorno (digamos, el espacio libre) puede ser utilizada como interferómetro Fabry-Pérot de alta Q (Fig. 31), debido a una reflexión de onda efectiva desde sus superficies a incidencia normal y especialmente inclinada — véanse, respectivamente, las ecuaciones (68), y las ecuaciones (91) y (95).

Fig. 7.31. Un interferómetro dieléctrico de Fabry-Pérot.

En realidad, tales interferómetros dieléctricos de Fabry-Pérot son frecuentemente más convenientes para fines prácticos que los resonadores de pared metálica, no solo debido a pérdidas posiblemente menores (especialmente en el rango óptico), sino también debido a un acoplamiento natural al entorno, que permite una forma fácil de inserción de ondas y extracción — ver Fig. 31 de nuevo. El reverso de la misma medalla es que este acoplamiento al ambiente proporciona un mecanismo adicional de pérdidas de potencia, limitando la calidad de resonancia — ver la siguiente sección.

---

Referencia

⁷⁹ El dispositivo lleva el nombre de sus inventores, Charles Fabry y Alfred Pérot; también se llama el etalón Fabry-Pérot (que significa “calibre”), debido a su uso inicial para las mediciones de la longitud de onda de la luz.

⁸⁰ Los resonadores formados por paredes bien conductoras (generalmente metálicas) se denominan frecuentemente cavidades resonantes.

⁸¹ Esta es, por supuesto, la expresión de la primera de las condiciones generales de contorno (104). La segunda de estas condiciones (para el campo magnético) se satisface automáticamente para las ondas transversales que estamos considerando.

⁸² En la mayoría de los manuales de ingeniería eléctrica, el índice correspondiente al lado más corto del resonador se enumera en último lugar, de manera que el modo fundamental se\(\ H_{110}\) nombra como y su frecuencia propia como\(\ \omega_{110}\).

⁸³ Este hecho se hace evidente al enchufar las ecuaciones (208) a la ecuación de Maxwell\(\ \nabla \cdot \mathbf{E}=0\). La ecuación resultante\(\ k_{x} E_{1}+k_{y} E_{2}+k_{z} E_{3}=0\), con el espectro discreto equidistante (209) para cada componente del vector de onda, puede ser satisfecha por dos conjuntos linealmente independientes de las constantes\(\ E_{1,2,3}\).

⁸⁴ Véase, por ejemplo, QM Sec. 1.1 y SM Sec. 2.6.