10.3: Radiación de Sincrotrón

Ahora consideremos que una partícula cargada se acelera en la dirección perpendicular a su velocidad u (por ejemplo por la componente magnética de la fuerza Lorentz), de manera que su velocidad\(\ u\), y de ahí la magnitud\(\ p\) de su impulso, no cambien. En este caso, el segundo término entre corchetes de la Ec. (39) se desvanece, y rinde

\[\ \mathscr{P}=\frac{Z_{0} q^{2}}{6 \pi m^{2} c^{2}}\left(\frac{d \mathbf{p}}{d \tau}\right)^{2}=\frac{Z_{0} q^{2}}{6 \pi m^{2} c^{2}}\left(\frac{d \mathbf{p}}{d t_{\mathrm{ret}}}\right)^{2} \gamma^{2}.\tag{10.43}\]

Comparando esta expresión con la Ec. (40), vemos que para la misma magnitud de aceleración, la radiación electromagnética es un factor de\(\ \gamma^{2}\) mayor. Para los aceleradores modernos\(\ \gamma \sim 10^{4}-10^{5}\), con, tal factor crea una enorme diferencia. Por ejemplo, si una partícula está en una órbita de ciclotrón en un campo magnético constante (como se analizó en la Sec. 9.6), tanto u como\\(\ \mathbf{p}=\gamma m \mathbf{u}\) obedecen la Ec. (9.150), de manera que

\[\ \left|\frac{d \mathbf{p}}{d t_{\mathrm{ret}}}\right|=\omega_{\mathrm{c}} p=\frac{u}{R} p=\beta^{2} \gamma \frac{m c^{2}}{R},\tag{10.44}\]

(donde\(\ R\) está el radio de la órbita), de manera que para la potencia de esta radiación de sincrotrón, la Eq. (43) rinde

\[\ \mathscr{P}=\frac{Z_{0} q^{2}}{6 \pi} \beta^{4} \gamma^{4} \frac{c^{2}}{R^{2}}.\quad\quad\quad\quad\text{Synchrotron radiation: total power}\tag{10.45}\]

De acuerdo con la Ec. (9.153), en un campo magnético fijo (en aceleradores de partículas, limitado a campos de a-pocas teslas de los imanes de flexión de haz), el radio de la órbita del sincrotrón\(\ R\) escala como\(\ \gamma\), de manera que según la Ec. (45),\(\ \mathscr{P}\) escala como\(\ \gamma^{2}\), es decir, crece como el cuadrado de la partícula energía\(\ \mathscr{E} \propto \gamma\). Por ejemplo, para parámetros típicos de los primeros ciclotrones de electrones (como la máquina de General Electric en que la radiación de sincrotrón se notó por primera vez en 1947),\(\ R \sim 1 \mathrm{~m}, \mathscr{E} \sim 0.3 \mathrm{GeV}(\gamma \sim 600)\), Eq. (45) da una pérdida de energía electrónica muy modesta por una revolución:\(\ \mathscr{P} \mathcal{T} \equiv \mathscr{P}(2 \pi R / u) \approx 2 \pi \mathscr{P} R / c \sim 1 \mathrm{keV}\). Sin embargo, ya a mediados de la década de 1970, los aceleradores de electrones\(\ R \sim 100 \mathrm{~m}\), con, podrían dar energía a cada partícula\(\ \mathscr{E} \sim 10 \mathrm{GeV}\), y la pérdida de energía por revolución creció hasta\(\ \sim 10 \mathrm{MeV}\) convertirse en el principal mecanismo de pérdida de energía. Para los aceleradores de protones, dicha pérdida de energía es un problema mucho menor, debido\(\ \gamma\) a que una partícula ultrarrelativista (en fijo\(\ \mathscr{E}\)) es proporcional a\(\ 1 / \mathrm{m}\), por lo que las estimaciones\(\ R\), al mismo tiempo, deben ser reducidas por\(\ \left(m_{\mathrm{p}} / m_{\mathrm{e}}\right)^{4} \sim 10^{13}\). Sin embargo, en los aceleradores gigantes modernos como el ya mencionado LHC (con\(\ R \approx 4.3 \mathrm{~km}\) y\(\ \mathscr{E}\) hasta 7 TeV), la pérdida de radiación de sincrotrón por revolución es bastante notable\(\ (\mathscr{P}\mathcal{T} \sim 6 \mathrm{keV})\), conduciendo no tanto a la desaceleración de partículas como a una emisión sustancial de fotoelectrones del haz paredes del tubo, creando efectos nocivos de desenfoque.

Sin embargo, lo que es malo para los aceleradores de partículas y los anillos de almacenamiento es bueno para las llamadas fuentes de luz sincrotrón —los aceleradores de electrones diseñados especialmente para la generación de radiación intensiva de sincrotrón— con el espectro extendiéndose mucho más allá del rango de luz visible. Analicemos las distribuciones angulares y espectrales de dicha radiación. Para calcular la distribución angular, seleccionemos los ejes de coordenadas como se muestra en la Fig. 5, con el origen en la ubicación actual de la partícula orbitante, el eje z dirigido a lo largo de su velocidad instantánea (es decir, el vector\(\ \boldsymbol{\beta}\)), y el eje x, hacia el centro de la órbita.

Fig. 10.5. La geometría del problema de la radiación sincrotrónica.

En el caso general, cuando el vector unitario n hacia el observador de la radiación no se encuentra dentro de ninguno de los planos de coordenadas, tiene que ser descrito por dos ángulos: el ángulo polar\(\ \theta\), y el ángulo azimutal\(\ \varphi\) entre el eje x y la proyección 0P del vector n a el avión\(\ [x, y]\). Dado que la longitud del segmento 0P es\(\ \sin \theta\), los componentes cartesianos de los vectores relevantes son los siguientes:

\[\ \mathbf{n}=\{\sin \theta \cos \varphi, \sin \theta \sin \varphi, \cos \theta\}, \quad \boldsymbol{\beta}=\{0,0, \beta\}, \quad \text { and } \dot{\boldsymbol{\beta}}=\{\dot{\beta}, 0,0\}.\tag{10.46}\]

Al enchufar estas expresiones a la ecuación general (30), obtenemos

\ [\\ text {Radiación sincrotrón: distribución angular}\ quad\ quad\ quad\ quad\ begin {reunidos}
\ frac {d\ mathscr {P}} {d\ Omega} =\ frac {2 Z_ {0} q^ {2}} {\ pi^ {2}} |\ punto {\ negrita {\ beta}} |^ {2}\ gamma^ {6} f (\ theta,\ varphi),\ quad\ texto {donde}\\
f (\ theta,\ varphi)\ equiv\ frac {1} {8\ gamma^ { 6} (1-\ beta\ cos\ theta) ^ {3}}\ izquierda [1-\ frac {\ sin ^ {2}\ theta\ cos ^ {2}\ varphi} {\ gamma^ {2} (1-\ beta\ cos\ theta) ^ {2}}\ derecha]
\ end {reunidos},\ tag {10.47}\]

Según este resultado, así como en la aceleración lineal, en el límite ultrarrelativista, la mayor parte de la radiación entra en un cono estrecho (de una anchura\(\ \Delta \theta \sim \gamma^{-1}<<1\)) alrededor del vector\(\ \boldsymbol{\beta}\), es decir, alrededor de la dirección instantánea de propagación de la partícula. Para ángulos tan pequeños\(\ \gamma >> 1\), y

\[\ f(\theta, \varphi) \approx \frac{1}{\left(1+\gamma^{2} \theta^{2}\right)^{3}}\left[1-\frac{4 \gamma^{2} \theta^{2} \cos ^{2} \varphi}{\left(1+\gamma^{2} \theta^{2}\right)^{2}}\right].\tag{10.48}\]

El panel izquierdo de la figura 6 muestra un mapa de contorno codificado por colores de esta distribución angular\(\ f(\theta, \varphi)\), tal como se observa en un plano distante normal a la velocidad instantánea de la partícula (en la figura 5, paralelo al plano\(\ [x, y]\)), mientras que su panel derecho muestra el factor\(\ f\) en función de\(\ \theta\) en dos direcciones perpendiculares: dentro del plano de
rotación de la partícula (en la dirección paralela al eje x, es decir, at\(\ \varphi=0\)) y perpendicular a este plano (a lo largo del eje y, es decir, at\(\ \varphi=\pm \pi / 2\)). El resultado muestra, en primer lugar, que, en contraste con el caso de la aceleración lineal, el cono estrecho de radiación ahora no es hueco: la intensidad máxima se alcanza en\(\ \theta=0\), es decir, exactamente en la dirección de la dirección de movimiento de la partícula. Segundo, el cono de radiación no es axialmente simétrico: dentro del plano de rotación de partículas, la intensidad cae más rápido (e incluso tiene nodos en\(\ \theta=\pm 1 / \gamma\)).

Fig. 10.6. La distribución angular de la radiación de sincrotrón en\(\ \gamma >> 1\).

Como muestra la figura 5, se calculó la distribución angular (47) de la radiación sincrotrón para el marco de referencia (inercial) cuyo origen coincide con la posición de la partícula en este instante particular, es decir, su patrón de radiación es independiente del tiempo en el marco que se mueve con la partícula. Este patrón permite una descripción semicuantitativa de la radiación por una partícula ultrarrelativista desde el punto de vista de un observador estacionario: si el punto de observación está en (o muy cerca) del plano de rotación, ¹¹ está siendo “golpeado” por el cono de radiación estrecho una vez cada uno periodo de rotación\(\ \mathcal{T} \approx 2 \pi R / c\), cada “golpe” dando un pulso de campo de corta duración\(\ \Delta t_{\mathrm{ret}}<<1 / \omega_{\mathrm{c}}\) - ver Fig. 7. ¹²

Fig. 10.7. (a) Los conos de radiación sincrotrón (at\(\ \gamma >> 1\)) para dos valores cercanos de\(\ t_{\mathrm{ret}}\), y (b) el componente en el plano del campo eléctrico, observado en el plano de rotación, en función del tiempo\(\ t\) —esquemáticamente.

La evaluación del tiempo\(\ \Delta t\) de duración de cada pulso requiere cierto cuidado: su estimación\(\ \Delta t_{\mathrm{ret}} \sim 1 / \gamma \omega_{\mathrm{c}}\) es correcta para la duración del intervalo de tiempo retardado durante el cual su cono está dirigido al observador. Sin embargo, debido al efecto de compresión de tiempo discutido en detalle en la Sec. 1 y descrito por la Ec. (16), la duración del pulso vista por el observador es un factor de\(\ 1 /(1-\beta)\) menor, por lo que

\[\ \Delta t=(1-\beta) \Delta t_{\mathrm{ret}} \sim \frac{1-\beta}{\gamma \omega_{\mathrm{c}}} \sim \frac{1}{\gamma^{3} \omega_{\mathrm{c}}} \sim \gamma^{-3} \mathcal{T}, \quad \text { for } \gamma>>1.\tag{10.49}\]

Del teorema de Fourier, podemos esperar que el espectro de frecuencias de dicha radiación consista en numerosos\(\ \left(N \sim \gamma^{3} >> 1\right)\) armónicos de la frecuencia de rotación de partículas\(\ \omega_{\mathrm{c}}\), con amplitudes comparables. Sin embargo, si la frecuencia orbital fluctúa incluso ligeramente\(\ \left(\delta \omega_{\mathrm{c}} / \omega_{\mathrm{c}}>1 / N \sim 1 / \gamma^{3}\right)\), como ocurre en la mayoría de los sistemas prácticos, los pulsos de radiación no son coherentes, de manera que el espectro de potencia de radiación promedio puede calcularse como el de un pulso, multiplicado por el número de pulsos por segundo. En este caso, el espectro es continuo, extendiéndose desde bajas frecuencias hasta aproximadamente

\[\ \omega_{\max } \sim 1 / \Delta t \sim \gamma^{3} \omega_{\mathrm{c}}.\tag{10.50}\]

Para verificar y cuantificar este resultado, calculemos el espectro de radiación, debido a un solo pulso. Para ello, primero debemos hacer cuantitativa la noción general del espectro de radiación. Representemos un campo eléctrico arbitrario (digamos el de la radiación sincrotrón que estamos estudiando ahora), observado en un punto fijo r, en función del tiempo de observación\(\ t\), como una integral de Fourier: ¹³

\[\ \mathbf{E}(t)=\int_{-\infty}^{+\infty} \mathbf{E}_{\omega} e^{-i \omega t} d t.\tag{10.51}\]

Esta expresión se puede conectar a la fórmula para la energía total del pulso de radiación (es decir, de la pérdida de energía de la partícula\(\ \mathscr{E}\)) por unidad de ángulo sólido: ¹⁴

\[\ -\frac{d \mathscr{E}}{d \Omega} \equiv \int_{-\infty}^{+\infty} S_{n}(t) R^{2} d t=\frac{R^{2}}{Z_{0}} \int_{-\infty}^{+\infty}|\mathbf{E}(t)|^{2} d t.\tag{10.52}\]

Esta sustitución, seguida de un cambio natural del orden de integración, rendimiento

\[\ -\frac{d \mathscr{E}}{d \Omega}=\frac{R^{2}}{Z_{0}} \int_{-\omega}^{+\omega} d \omega \int_{-\omega}^{+\omega} d \omega^{\prime} \mathbf{E}_{\omega} \cdot \mathbf{E}_{\omega^{\prime}} \int_{-\infty}^{+\infty} d t e^{-i\left(\omega+\omega^{\prime}\right) t}.\tag{10.53}\]

Pero la integral interna (sobre\(\ t\)) es justa\(\ 2 \pi \delta\left(\omega+\omega^{\prime}\right)\). ¹⁵ Esta función delta mata una de las integrales de frecuencia (digamos, una sobre\(\ \omega’\)), y la ecuación (53) nos da un resultado que puede ser refundido como

\[\ -\frac{d \mathscr{E}}{d \Omega}=\int_{0}^{+\infty} I(\omega) d \omega, \quad \text { with } I(\omega) \equiv \frac{4 \pi R^{2}}{Z_{0}} \mathbf{E}_{\omega} \cdot \mathbf{E}_{-\omega} \equiv \frac{4 \pi R^{2}}{Z_{0}} \mathbf{E}_{\omega} \mathbf{E}_{\omega}^{*},\tag{10.54}\]

donde la simetría de frecuencia evidente del producto escalar se\(\ \mathbf{E}_{\omega} \cdot \mathbf{E}_{-\omega}\) ha utilizado para\(\ I(\omega)\) plegar la integral de frecuencias positivas solamente. La primera de las ecuaciones (54) deja\(\ I(\omega)\) muy claro el sentido físico de la función: esta es la llamada densidad espectral de la radiación electromagnética (por unidad de ángulo sólido). ¹⁶

Para calcular la densidad espectral, podemos expresar la función\(\ \mathbf{E}_{\omega}\) mediante el\(\ \mathbf{E}(t)\) uso de la transformada de Fourier recíproca a la Ec. (51):

\[\ \mathbf{E}_{\omega}=\frac{1}{2 \pi} \int_{-\infty}^{+\infty} \mathbf{E}(t) e^{i \omega t} d t.\tag{10.55}\]

En el caso particular de la radiación por una sola carga puntual, podemos usar aquí el segundo término (radiativo) de la Ec. (19):

\[\ \mathbf{E}_{\omega}=\frac{1}{2 \pi} \frac{q}{4 \pi \varepsilon_{0}} \frac{1}{c R} \int_{-\infty}^{+\infty}\left[\frac{\mathbf{n} \times\{(\mathbf{n}-\boldsymbol{\beta}) \times \dot{\boldsymbol{\beta}}\}}{(1-\boldsymbol{\beta} \cdot \mathbf{n})^{3}}\right]_{\mathrm{ret}} e^{i \omega t} d t.\tag{10.56}\]

Dado que los vectores n y\(\ \boldsymbol{\beta}\) son funciones más naturales del tiempo de radiación (retardado)\(\ t_{\mathrm{ret}}\), usemos las ecuaciones (5) y (16) para excluir el tiempo\(\ t\) de observación de esta integral:

\[\ \mathbf{E}_{\omega}=\frac{q}{4 \pi \varepsilon_{0}} \frac{1}{2 \pi} \frac{1}{c R} \int_{-\infty}^{+\infty}\left[\frac{\mathbf{n} \times\{(\mathbf{n}-\boldsymbol{\beta}) \times \dot{\boldsymbol{\beta}}\}}{(1-\boldsymbol{\beta} \cdot \mathbf{n})^{2}}\right]_{\mathrm{ret}} \exp \left\{i \omega\left(t_{\mathrm{ret}}+\frac{R_{\mathrm{ret}}}{c}\right)\right\} d t_{\mathrm{ret}}.\tag{10.57}\]

Suponiendo que el observador está lo suficientemente lejos de la partícula, ¹⁷ podemos tratar el vector unitario n como una constante y también usar la aproximación (8.19) para reducir la Ec. (57) a

\[\ \mathbf{E}_{\omega}=\frac{1}{2 \pi} \frac{q}{4 \pi \varepsilon_{0}} \frac{1}{c R} \exp \left\{\frac{i \omega r}{c}\right\} \int_{-\infty}^{+\infty}\left[\frac{\mathbf{n} \times\{(\mathbf{n}-\boldsymbol{\beta}) \times \dot{\boldsymbol{\beta}}\}}{(1-\boldsymbol{\beta} \cdot \mathbf{n})^{2}} \exp \left\{i \omega\left(t-\frac{\mathbf{n} \cdot \mathbf{r}^{\prime}}{c}\right)\right\}\right]_{\mathrm{ret}} d t_{\mathrm{ret}}.\tag{10.58}\]

Conectando esta expresión a la Eq. (54), y luego usando las definiciones\(\ c \equiv 1 /\left(\varepsilon_{0} \mu_{0}\right)^{1 / 2}\) y\(\ Z_{0} \equiv\left(\mu_{0} / \varepsilon_{0}\right)^{1 / 2}\), obtenemos ¹⁸

\[\ I(\omega)=\frac{Z_{0} q^{2}}{16 \pi^{3}}\left|\int_{-\infty}^{+\infty}\left[\frac{\mathbf{n} \times\{(\mathbf{n}-\boldsymbol{\beta}) \times \dot{\boldsymbol{\beta}}\}}{(1-\boldsymbol{\beta} \cdot \mathbf{n})^{2}} \exp \left\{i \omega\left(t-\frac{\mathbf{n} \cdot \mathbf{r}^{\prime}}{c}\right)\right\}\right]_{\mathrm{ret}} d t_{\mathrm{ret}}\right|^{2}.\tag{10.59}\]

Este resultado puede simplificarse aún más al observar que la fracción anterior al exponente puede representarse como una derivada completa sobre\(\ t_{\mathrm{ret}}\),

\[\ \left[\frac{\mathbf{n} \times\{(\mathbf{n}-\boldsymbol{\beta}) \times \dot{\boldsymbol{\beta}}\}}{(1-\boldsymbol{\beta} \cdot \mathbf{n})^{2}}\right]_{\mathrm{ret}} \equiv\left[\frac{\mathbf{n} \times\{(\mathbf{n}-\boldsymbol{\beta}) \times d \boldsymbol{\beta} / d t\}}{(1-\boldsymbol{\beta} \cdot \mathbf{n})^{2}}\right]_{\mathrm{ret}} \equiv \frac{d}{d t}\left[\frac{\mathbf{n} \times(\mathbf{n} \times \boldsymbol{\beta})}{1-\boldsymbol{\beta} \cdot \mathbf{n}}\right]_{\mathrm{ret}},\tag{10.60}\]

y elaboración de la integral resultante por partes. En esta operación, da la diferenciación temporal de los paréntesis en el exponente\(\ d\left[t_{\mathrm{ret}}-\mathbf{n} \cdot \mathbf{r}^{\prime}\left(t_{\mathrm{ret}}\right) / c\right] / d t_{\mathrm{ret}}=(1-\mathbf{n} \cdot \mathbf{u} / c)_{\mathrm{ret}} \equiv(1-\boldsymbol{\beta} \cdot \mathbf{n})_{\mathrm{ret}}\), lo que lleva a la cancelación del factor restante en el denominador y de ahí a un resultado general muy simple: ¹⁹

\[\ \text{Relativistic radiation: spectral density}\quad\quad\quad\quad I(\omega)=\frac{Z_{0} q^{2} \omega^{2}}{16 \pi^{3}}\left|\int_{-\infty}^{+\infty}\left[\mathbf{n} \times(\mathbf{n} \times \boldsymbol{\beta}) \exp \left\{i \omega\left(t-\frac{\mathbf{n} \cdot \mathbf{r}^{\prime}}{c}\right)\right\}\right]_{\mathrm{ret}} d t_{\mathrm{ret}}\right|^{2}.\tag{10.61}\]

Ahora volviendo al caso particular de la radiación sincrotrón, es beneficioso elegir el origen del tiempo para\(\ t_{\mathrm{ret}}\) que en\(\ t_{\mathrm{ret}}=0\), el ángulo\(\ \theta\) entre los vectores n y\(\ \boldsymbol{\beta}\) tome su valor más pequeño\(\ \theta_{0}\), es decir, en términos de la Fig. 5, el vector n está dentro del avión\(\ [y, z]\). Fijando esta dirección de los ejes, para que no se muevan en más tiempos, podemos redibujar esa figura como se muestra en la Fig. 8.

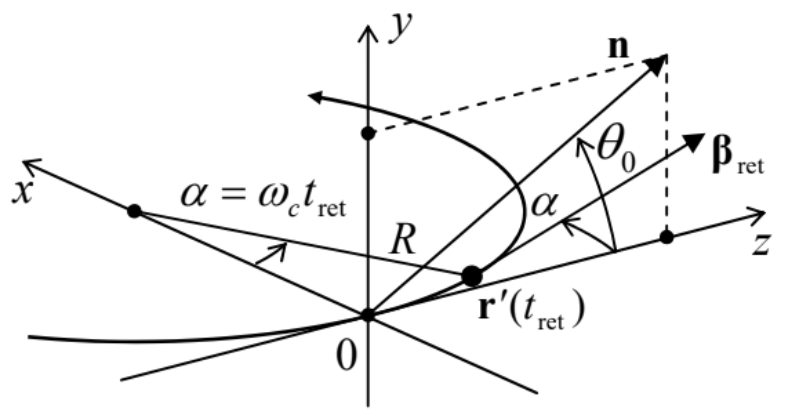
Fig. 10.8. Derivando la densidad espectral de la radiación sincrotrónica. El vector n es estático dentro del plano\(\ [y, z]\), mientras que los vectores\(\ \mathbf{r}^{\prime}\left(t_{\mathrm{ret}}\right)\) y\(\ \boldsymbol{\beta}_{\text {ret }}\) rotan, dentro del plano\ (\\ izquierda [\ begin {array} {ll}
x, & z
\ end {array}\ right]\), con la velocidad angular\(\ \omega_{c}\) de la partícula.

En este marco de referencia “lab”, el vector n no depende del tiempo, mientras que los vectores\(\ \mathbf{r}^{\prime}\left(t_{\mathrm{ret}}\right)\) y\(\ \boldsymbol{\beta}_{\mathrm{ret}}\) sí dependen de él a través del ángulo\(\ \alpha \equiv \omega_{\mathrm{c}} t_{\mathrm{ret}}\):,

\[\ \mathbf{n}=\left\{0, \sin \theta_{0}, \cos \theta_{0}\right\}, \quad \mathbf{r}^{\prime}\left(t_{\mathrm{ret}}\right)=\{R(1-\cos \alpha), 0, R \sin \alpha\}, \quad \boldsymbol{\beta}_{\mathrm{ret}} \equiv\{\beta \sin \alpha, 0, \beta \cos \alpha\}.\tag{10.62}\]

Ahora una fácil multiplicación rinde

\[\ [\mathbf{n} \times(\mathbf{n} \times \boldsymbol{\beta})]_{\mathrm{ret}}=\beta\left\{\sin \alpha, \sin \theta_{0} \cos \theta_{0} \cos \alpha,-\sin ^{2} \theta_{0} \sin \alpha\right\},\tag{10.63}\]

\[\ \left[\exp \left\{i \omega\left(t-\frac{\mathbf{n} \cdot \mathbf{r}^{\prime}}{c}\right)\right\}\right]_{\mathrm{ret}}=\exp \left\{i \omega\left(t_{\mathrm{ret}}-\frac{R}{c} \cos \theta_{0} \sin \alpha\right)\right\}.\tag{10.64}\]

Como ya sabemos, en el límite ultrarrelativista (más interesante)\(\ \gamma >> 1\), la mayor parte de la radiación se limita a pulsos cortos, de manera que solo pequeños ángulos\(\ \alpha \sim \omega_{\mathrm{c}} \Delta t_{\mathrm{ret}} \sim \gamma^{-1}\) pueden contribuir a la integral en la Ec. (61). Además, dado que la mayor parte de la radiación va a ángulos pequeños\(\ \theta \sim \theta_{0} \sim \gamma^{-1}\), tiene sentido considerar solo ángulos tan pequeños. Ampliando ambas funciones trigonométricas de estos pequeños ángulos, participando entre paréntesis de la ecuación (64), en la serie Taylor, y manteniendo solo los términos principales, obtenemos

\[\ t_{\mathrm{ret}}-\frac{R}{c} \cos \theta_{0} \sin \alpha \approx t_{\mathrm{ret}}-\frac{R}{c} \omega_{\mathrm{c}} t_{\mathrm{ret}}+\frac{R}{c} \frac{\theta_{0}^{2}}{2} \omega_{\mathrm{c}} t_{\mathrm{ret}}+\frac{R}{c} \frac{\omega_{\mathrm{c}}^{3}}{6} t_{\mathrm{ret}}^{3}.\tag{10.65}\]

Ya que\(\ (R / c) \omega_{\mathrm{c}}=u / c=\beta \approx 1\), en los dos últimos términos podemos aproximar este parámetro por 1. No obstante, es crucial distinguir la diferencia de los dos primeros términos, proporcional a\(\ (1-\beta) t_{\mathrm{ret}}\), de cero; como hemos hecho antes, podemos aproximarlo con\(\ t_{\mathrm{ret}} / 2 \gamma^{2}\). En el lado derecho de la Ec. (63), que no tiene una diferencia tan crítica, podemos ser más audaces, tomando ²⁰

\[\ \beta\left\{\sin \alpha, \sin \theta_{0} \cos \theta_{0} \cos \alpha,-\sin ^{2} \theta_{0} \sin \alpha\right\} \approx\left\{\alpha, \theta_{0}, 0\right\} \equiv\left\{\omega_{\mathrm{c}} t_{\mathrm{ret}}, \theta_{0}, 0\right\}.\tag{10.66}\]

Como resultado, la ecuación (61) se reduce a

\[\ I(\omega)=\frac{Z_{0} q^{2}}{16 \pi^{3}}\left|a_{x} \mathbf{n}_{x}+a_{y} \mathbf{n}_{y}\right|^{2} \equiv \frac{Z_{0} q^{2}}{16 \pi^{3}}\left(\left|a_{x}\right|^{2}+\left|a_{y}\right|^{2}\right),\tag{10.67}\]

donde\(\ a_{x}\) y\(\ a_{y}\) son los siguientes factores adimensionales:

Radiación sincrotrón: densidad espectral

\ [\\ begin {alineado}
&a_ {x}\ equiv\ omega\ int_ {-\ infty} ^ {+\ infty}\ omega_ {\ mathrm {c}} t_ {\ mathrm {ret}}\ exp\ izquierda\ {\ frac {i\ omega} {2}\ izquierda (\ izquierda (\ theta_ {0} ^ {2} +\ gamma^ {-2}\ derecha) t_ {\ mathrm {ret}} +\ frac {\ omega_ {\ mathrm {c}} ^ {2}} {3} t_ {\ mathrm {ret}} ^ {3}\ derecha)\ derecha\} d t_ {\ mathrm {ret}},\\
&a_ {y}\ equiv\ omega\ int_ {-\ infty} ^ {+\ infty}\ theta_ {0}\ exp\ izquierda\ {\ frac {i\ omega} {2}\ izquierda (\ izquierda (\ theta_ {0} ^ {2} +\ gamma^ {-2}\ derecha) t_ {\ mathrm {ret}} +\ frac {\ omega_ {\ mathrm {c}} ^ {2}} {3} t_ {\ mathrm {ret}} ^ {3}\ derecha)\ derecha\} d t_ {\ mathrm {ret}},
\ end {alineado}\ tag {10.68}\]

que describen los espectros de frecuencia de dos componentes de la radiación sincrotrón, con direcciones de polarización mutuamente perpendiculares. Definición del siguiente parámetro adimensional

\[\ \nu \equiv \frac{\omega}{3 \omega_{\mathrm{c}}}\left(\theta_{0}^{2}+\gamma^{-2}\right)^{3 / 2},\tag{10.69}\]

que es proporcional a la frecuencia de observación, y cambiando la variable de integración a\(\ \xi\equiv \omega_{\mathrm{c}} t_{\mathrm{ret}} /\left(\theta_{0}^{2}+\gamma^{-2}\right)^{1 / 2}\), las integrales (68) pueden reducirse a las funciones Bessel modificadas del segundo tipo, pero con índices fraccionarios:

\ [\\ comenzar {alineado}
&a_ {x} =\ frac {\ omega} {\ omega_ {c}}\ izquierda (\ theta_ {0} ^ {2} +\ gamma^ {-2}\ derecha)\ int_ {-\ infty} ^ {+\ infty}\ xi\ exp\ izquierda\ {\ frac {3} {2} i\ nu izquierda (\ xi+\ frac {\ xi^ {3}} {3}\ derecha)\ derecha\} d\ xi=\ frac {2\ sqrt {3} i} {\ izquierda (\ theta_ {0} ^ {2} +\ gamma^ {-2}\ derecha) ^ {1/2}}\ nu K_ {2/3} (\ nu)\
&a_ {y} =\ frac {\ omega} {\ omega_ {c}}\ theta_ {0}\ izquierda (\ theta_ {0} ^ {2} +\ gamma^ {-2}\ derecha) ^ {1/2}\ int_ {-\ infty} ^ {+\ infty}\ exp\ izquierda\ {\ frac {3} {2} i\ nu\ izquierda (\ xi+\ frac {\ xi^ {3}} {3}\ derecha)\ derecha\} d\ xi=\ frac {2\ sqrt {3}\ theta_ {0}} {\ theta_ {0} ^ {2} +\ gamma^ {-2}}\ nu K_ {1/3} (\ nu)
\ end { alineado}\ tag {10.70}\]

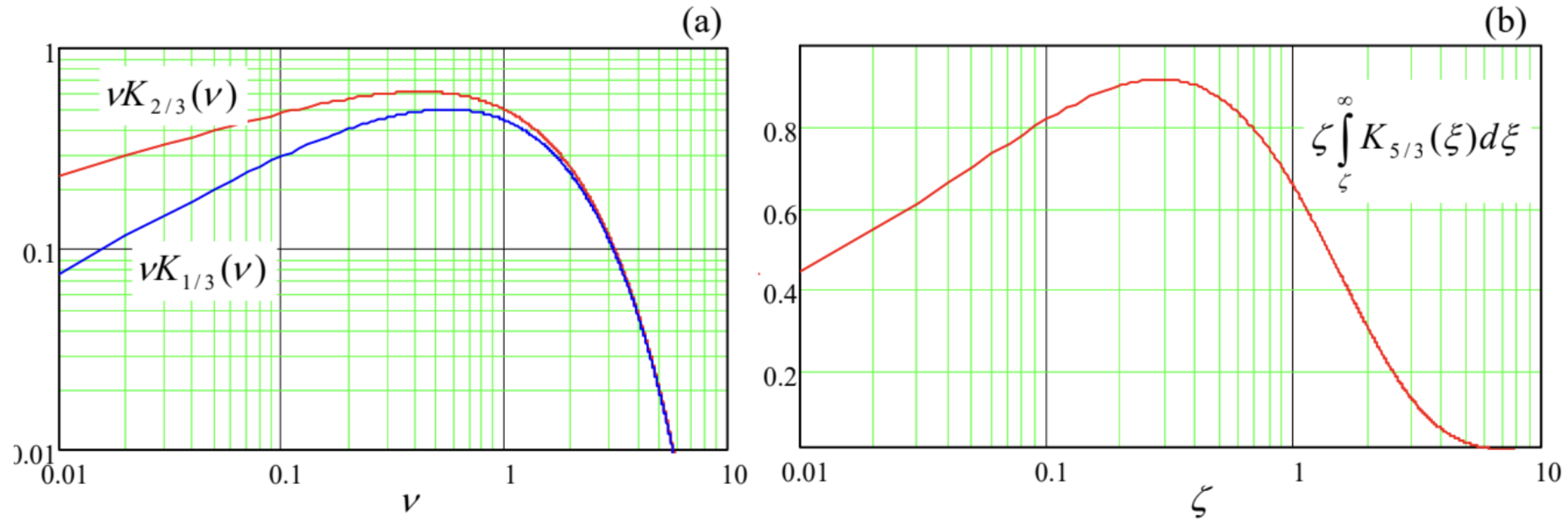
La Figura 9a muestra la dependencia de los factores de Bessel, definiendo las amplitudes ax y ay, de la frecuencia de observación normalizada\(\ \nu\). Muestra que la intensidad de la radiación cambia con la frecuencia de manera relativamente lenta (¡fíjese en la escala log-log de la parcela!) hasta que la frecuencia normalizada, definida por la Ec. (69), se incremente más allá de ~1. Para los ángulos de observación más importantes\(\ \theta_{0} \sim \gamma\) esto significa que nuestra estimación (50) es realmente correcta, aunque formalmente el espectro de frecuencias se extiende hasta el infinito. ²¹

Fig. 10.9. Los espectros de frecuencia de: (a) dos componentes de la radiación sincrotrón\(\ \theta_{0}\), en ángulo fijo, y (b) su intensidad total (polarización y ángulo promediada).

Naturalmente, la densidad espectral integrada sobre el ángulo sólido completo exhibe un comportamiento de frecuencia similar. Sin realizar la integración, ²² permítanme simplemente dar el resultado (también válido por\(\ \gamma>>1\) solo) para la referencia del lector:

\[\ \oint_{4 \pi} I(\omega) d \Omega=\frac{\sqrt{3}}{4 \pi} q^{2} \gamma \zeta \int_{\zeta}^{\infty} K_{5 / 3}(\xi) d \xi, \quad \text { where } \zeta \equiv \frac{2}{3} \frac{\omega}{\omega_{c} \gamma^{3}}.\tag{10.71}\]

La Figura 9b muestra la dependencia de esta integral de la frecuencia normalizada\(\ \zeta\). (Esta gráfica a veces se llama la “curva de flujo universal”). De acuerdo con la estimación (50), alcanza el máximo en

\[\ \zeta_{\max } \approx 0.3, \quad \text { i.e. } \omega_{\max } \approx \frac{\omega_{\mathrm{c}}}{2} \gamma^{3}.\tag{10.73}\]

Por ejemplo, en la Fuente Nacional de Luz Sincrotrón (NSLS-II) en el Laboratorio Nacional Brookhaven, cerca del campus SBU, con la circunferencia del anillo de 792 m, el periodo de revolución electrónica\(\ \mathcal{T}\) es de 2.64 μs. Calculando\(\ \omega_{\mathrm{c}}\) como\(\ 2 \pi / \mathcal{T} \approx 2.4 \times 10^{6} \mathrm{~s}^{-1}\), para lo logrado\(\ \gamma \approx 6 \times 10^{3}(\mathscr{E} \approx 3 \mathrm{GeV})\), obtenemos\(\ \omega_{\max }\sim 3\times10^{17}s^{-1}\) (la energía fotónica\(\ \hbar \omega_{\max } \sim 200 \mathrm{eV}\)), correspondiente a los rayos X blandos. A la luz de esta estimación, el lector puede sorprenderse con la Fig. 10, que muestra los espectros calculados de la radiación que esta instalación fue diseñada para producir, con los máximos de intensidad a las energías fotónicas de hasta unos pocos keV.

Fig. 10.10. Diseño de brillo de diversas fuentes de radiación sincrotrón de la instalación NSLS-II. Para los imanes curvados y meneadores, el “brillo” se puede obtener por multiplicación de la densidad espectral\(\ I(\omega)\) a partir de un pulso de electrones, calculado anteriormente, por el número de electrones que pasan por la fuente por segundo. (Obsérvese las unidades no SI utilizadas por la comunidad de radiación sincrotrón.) Sin embargo, para los onduladores, existe un factor adicional debido a la coherencia parcial de la radiación — ver más abajo. (Adaptado de NSLS-II Source Properties and Floor Layout, estuvo disponible en línea en https://www.bnl.gov/ps/docs/pdf/SourceProperties.pdf en 2011-2010.)

La razón de esta discrepancia es que en el NLLS-II, y en todas las fuentes de luz sincrotrón modernas, la mayor parte de la radiación es producida no por la órbita circular misma (que, por cierto, no es exactamente circular, sino que consiste en una serie de secciones rectas y curva-imán), sino por tales secciones curvas, y los dispositivos llamados meneadores y onduladores: cuerdas de varios imanes fuertes con dirección de campo alterno (Fig. 11), que inducen flexión periódica (meneo”) de la trayectoria del electrón, con la radiación sincrotrónica emitida en cada curva.

Fig. 10.11. La estructura genérica de los wigglers, onduladores y láseres de electrones libres. (Adaptado de http://www.xfel.eu/overview/how_does_it_work/.)

La diferencia entre los meneadores y los onduladores es más cuantitativa que cualitativa: los primeros dispositivos tienen un periodo espacial mayor\(\ \lambda_{\mathrm{u}}\) (la distancia entre los imanes adyacentes de la misma polaridad, ver Fig. 11), dando suficiente espacio para que el haz de electrones se doble en un ángulo mayor que \(\ \gamma^{-1}\), es decir,
mayor que el ancho del cono de radiación. Como resultado, la radiación llega a un observador en el plano como una secuencia periódica de pulsos individuales — ver Fig. 12a.

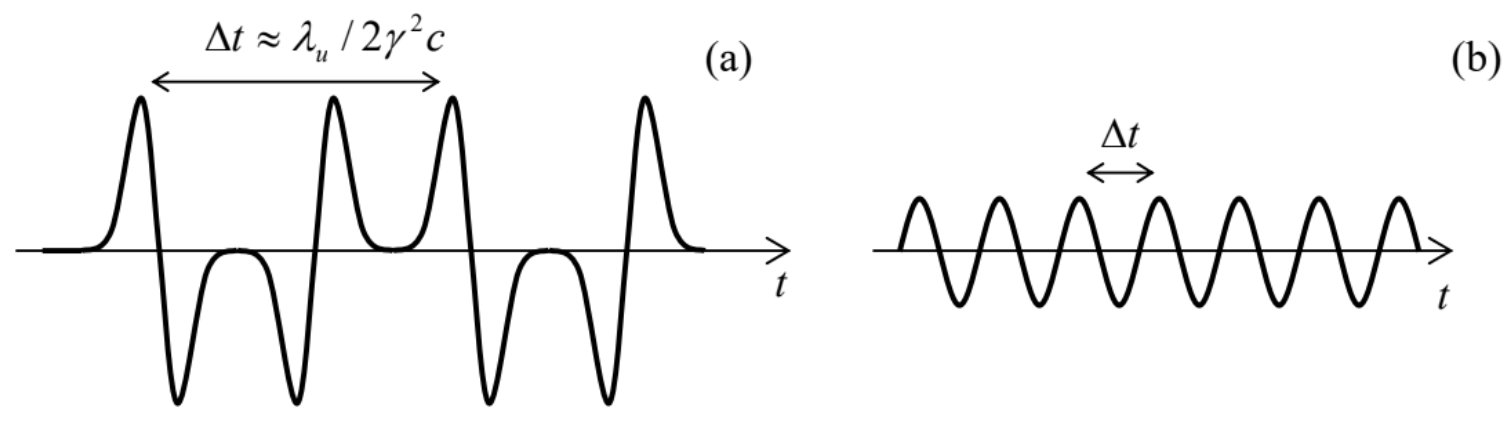Fig. 10.12. Formas de onda de la radiación emitida por (a) un ondulador y (b) un ondulador — esquemáticamente.

La forma de cada pulso, y por lo tanto su espectro de frecuencias, son esencialmente similares a las discutidas anteriormente, ²³ pero con valores locales mucho más altos de\(\ \omega_{\mathrm{c}}\) y por lo tanto\(\ \omega_{\max }\) — ver Fig. 10. Otra diferencia es una frecuencia mucho mayor de los pulsos. En efecto, la ecuación fundamental (16) nos permite calcular la distancia de tiempo entre ellos, para el observador, como

\[\ \Delta t \approx \frac{\partial t}{\partial t_{\text {ret }}} \Delta t_{\text {ret }} \approx(1-\beta) \frac{\lambda_{\mathrm{u}}}{u} \approx \frac{1}{2 \gamma^{2}} \frac{\lambda_{\mathrm{u}}}{c}<<\frac{\lambda_{\mathrm{u}}}{c},\tag{10.73}\]

donde las dos primeras relaciones son válidas en\(\ \lambda_{\mathrm{u}}<<R\) (la relación típicamente satisfecha muy bien, ver los números en la Fig. 10), y las dos últimas relaciones asumen el límite ultrarrelativista. En consecuencia, la intensidad de la radiación, que es proporcional al número de polos, es mucho mayor que la de los imanes curvados —véase nuevamente la Fig. 10.

La situación es diferente en los onduladores —estructuras similares con un periodo espacial menor\(\ \lambda_u\), en las que el vector de velocidad del electrón oscila con una amplitud angular menor que\(\ \gamma^{-1}\). Como resultado, los pulsos de radiación se superponen (Fig. 12b) y la forma de onda de radiación está más cerca de la sinusoidal. Como resultado, el espectro de radiación se estrecha a la frecuencia central ²⁴

\[\ \omega_{0}=\frac{2 \pi}{\Delta t} \approx 2 \gamma^{2} \frac{2 \pi c}{\lambda_{u}}.\tag{10.74}\]

Por ejemplo, para los onduladores LSNL-II con\(\ \lambda_{\mathrm{u}}=2 \mathrm{~cm}\), esta fórmula predice un pico de radiación a la energía fonónica\(\ \hbar \omega_{0} \approx 4 \mathrm{keV}\), en un acuerdo razonable con los resultados de los cálculos cuantitativos, mostrados en la Fig. 10. ²⁵ Debido al estrechamiento del espectro, la intensidad de la radiación del ondulador es mayor que la de los wigglers que utilizan el mismo haz de electrones.

Esta tendencia de estrechamiento del espectro se lleva a su conclusión lógica en los llamados láseres de electrones libres ²⁶ cuya estructura básica es la misma que la de los wigglers y unduladores (Fig. 11), pero la radiación en cada curva del haz es tan intensa y de enfoque estrecho que afecta al electrón movimiento aguas abajo del cono de radiación. Como resultado, el espectro de radiación se estrecha alrededor de la frecuencia central (74), y su potencia crece como un cuadrado del número N de electrones en la estructura (en lugar de proporcionalmente a N en meneadores y onduladores).

Finalmente, tenga en cuenta que también se pueden usar wigglers, onduladores y láseres de electrones libres al final de un acelerador de electrones lineal (como SLAC) que, como se señaló anteriormente, puede proporcionar valores extremadamente altos de, y por lo tanto frecuencias de\(\ \gamma\) radiación, debido a la pequeñez de las pérdidas de energía de radiación en el etapa de aceleración de electrones. Muy desafortunadamente, no tengo tiempo/espacio para discutir (muy interesante) la física de estos dispositivos con más detalle. ²⁷

---

Referencia

¹¹ Es fácil (y por lo tanto se deja para el ejercicio del lector) demostrar que si el punto de observación está mucho fuera del plano (digamos, se encuentra en el eje de la órbita de las partículas), la radiación es prácticamente monocromática, con frecuencia\(\ \omega_{c}\). (Como sabemos por la Sec. 8.2, en el límite no relativista\(\ u<<c\) esto es cierto para cualquier punto de observación.)

¹² El hecho de que la componente en el plano del pulso de cada campo eléctrico\(\ \mathbf{E}(t)\) sea antisimétrica con respecto a su punto central, y por lo tanto se desvanezca en ese punto (como muestra la Fig. 7b), se desprende fácilmente de la Ec. (19).

¹³ A diferencia del caso de frecuencia única (es decir, una onda monocromática), podemos evitar tomar la parte real de la función compleja\(\ \left(\mathbf{E}_{\omega} e^{-i \omega t}\right)\) al requerir que en la Ec. (51),\(\ \mathbf{E}_{-\omega}=\mathbf{E}_{\omega}^{*}\). Sin embargo, es importante recordar el factor 1⁄2 requerido para la transición a una onda monocromática de frecuencia\(\ \omega_{0}\) y con amplitud real\(\ \mathbf{E}_{0}\):\(\ \mathbf{E}_{\omega}=\mathbf{E}_{0}\left[\delta\left(\omega-\omega_{0}\right)+\delta\left(\omega+\omega_{0}\right)\right] / 2\)

¹⁴ Obsérvese que la expresión bajo esta integral difiere de la\(\ d \mathscr{P} / d \Omega\) definida por la Ec. (29) por la ausencia del término\(\ (1-\boldsymbol{\beta} \cdot \mathbf{n})=\partial t_{\mathrm{ret}} / \partial t\) — véase la Ec. (16). Esto es natural porque ahora estamos calculando la energía de las olas que llega al punto de observación r durante el intervalo de tiempo\(\ dt\) en lugar de\(\ d t_{\mathrm{ret}}\).

¹⁵ Véase, por ejemplo, MA Ec. (14.4).

¹⁶ La noción de densidad espectral puede generalizarse fácilmente a procesos aleatorios; véase, por ejemplo, SM Sec. 5.4.

¹⁷ Según la estimación (49), para el pulso de una radiación de sincrotrón, esta restricción requiere que el observador esté mucho más\(\ \Delta r^{\prime} \sim c \Delta t \sim R / \gamma^{3}\) lejos que de la partícula. Con los valores\(\ R \sim 10^{4}\) y\(\ \gamma \sim 10^{5}\) mencionados anteriormente,\(\ \Delta r^{\prime} \sim10^{-11}\mathrm{m}\), por lo que se satisface este requisito para cualquier detector de radiación realista.

¹⁸ Obsérvese que para nuestros propósitos actuales de cálculo de la densidad espectral de radiación por una sola partícula, el factor\(\ \exp \{i \omega r / c\}\) ha sido cancelado. Sin embargo, como hemos visto en el Capítulo 8, este factor juega el papel central en la interferencia de la radiación de varias (muchas) fuentes. Dicha interferencia es importante, en particular, en los onduladores y láseres de electrones libres, los dispositivos que se discutirán (cualitativamente) a continuación.

¹⁹ En realidad, esta simplificación no es ocasional. De acuerdo con la Ec. (10b), la expresión bajo la derivada en la última forma de la Ec. (60) es solo el componente transversal del potencial del vector\(\ \boldsymbol{A}\) (dar o tomar un factor constante), y a partir de la discusión en la Sec. 8.2 sabemos que este componente determina la radiación dipolar eléctrica de la partícula, que domina el campo de radiación en nuestro caso actual de una partícula con una carga eléctrica distinta de cero.

²⁰ Esta expresión confirma que el componente en el plano (x) del campo eléctrico es una función impar de\(\ t_{\mathrm{ret}}\) y por lo tanto de\(\ t-t_{0}\) (ver su boceto en la Fig. 7b), mientras que el\(\ (y)\) componente normal es una función par de esta diferencia. También, tenga en cuenta que para un observador exactamente en\(\ \left(\theta_{0}=0\right)\) el plano de rotación este último componente equivale a cero para todos los tiempos, hecho que podría predecirse desde el principio debido a la evidente simetría especular del problema con respecto al plano de rotación de partículas.

²¹ La ley de la disminución de la densidad espectral en general\(\ \nu\) puede obtenerse fácilmente a partir de la segunda de las ecuaciones (2.158), que es válida incluso para cualquier índice de función de Bessel (incluso no entero)\(\ n\):\(\ a_{x} \propto a_{y} \propto \nu^{-1 / 2} \exp \{-\nu\}\). Aquí el factor exponencial es sin duda el más importante.

²² Para ello, y muchos otros detalles, el lector interesado puede ser referido, por ejemplo, a la colección de revisión fundamental de E. Koch et al. (eds.) Manual sobre Radiación Sincrotrónica (en 5 vols.), Holanda Septentrional, 1983-1991, o a una monografía más concisa de A. Hofmann, The Physics of Synchrotron Radiation, Cambridge U. Press, 2007.

²³ En efecto, el periodo\(\ \lambda_{u}\) suele ser de unos pocos centímetros (ver los números en la Fig. 10), es decir, es mucho mayor que el intervalo\(\ \Delta r^{\prime} \sim R / \gamma^{3}\) estimado anteriormente. Por lo tanto, los resultados de la radiación de sincrotrón pueden aplicarse localmente, a cada curva del haz de electrones. (En este contexto, un problema simple para el lector: utilizar las ecuaciones (19) y (63) para explicar la diferencia entre las formas de los pulsos de campo eléctrico en el plano emitidos en polos magnéticos opuestos del wiggler, que se muestra esquemáticamente en la Fig. 12a.)

²⁴ Esta importante fórmula también se puede derivar de la siguiente manera. Debido a la contracción relativista de longitud (9.20), el periodo de la estructura onduladora tal como se percibe por los electrones del haz es\(\ \lambda^{\prime}=\lambda_{u} / \gamma\), de manera que la frecuencia central de la radiación en el marco de referencia que se mueve con los electrones es\(\ \omega_{0}^{\prime}=2 \pi c / \lambda^{\prime}=2 \pi c \gamma / \lambda_{u}\). Para el observador de marco de laboratorio, esta frecuencia es Doppler desplazada hacia arriba de acuerdo con la Ec. (9.44):\(\ \omega_{0}=\omega_{0}{ }^{\prime}[(1+\beta) /(1-\beta)]^{1 / 2} \approx 2 \gamma \omega_{0}’\), dando el mismo resultado que la Ec. (74).

²⁵ Parte de la diferencia se debe a que esas gráficas muestran la densidad espectral del número de fotones\(\ n=\mathscr{E}/\hbar\omega\) por segundo, que alcanza su punto máximo a una frecuencia inferior a la de la densidad de potencia, es decir, de la energía\(\ \mathscr{E}\) por segundo.

²⁶ Este nombre es algo engañoso, porque a diferencia de los láseres habituales (“cuánticos”), un láser de electrones libres es esencialmente un dispositivo clásico, y la dinámica de los electrones en él es muy similar a la de los generadores de microondas de tubo de vacío, como los magnetrones discutidos brevemente en la Sec. 9.6.

²⁷ El lector interesado puede ser referido, por ejemplo, a P. Luchini y H. Motz, Onduladores y láseres de electrones libres, Oxford U. Press, 1990; o E. Salin et al., The Physics of Free Electron Lasers, Springer, 2000.