2.6: Fuerza y tensión normales

Objetivos de aprendizaje

• Definir fuerza normal.
• Explicar la relación entre la fuerza normal y el peso aparente.
• Describir las propiedades de la fuerza de tensión.
• Aplicar las leyes del movimiento de Newton para analizar fuerzas.

A las fuerzas se les dan muchos nombres, como empujar, tirar, empujar, levantar, peso, fricción y tensión. Tradicionalmente, las fuerzas se han agrupado en varias categorías y se les ha dado nombres relacionados con su fuente, cómo se transmiten o sus efectos. Las más importantes de estas categorías se discuten en esta sección, junto con algunas aplicaciones interesantes. Más adelante en este texto se discuten más ejemplos de fuerzas.

Fuerza Normal

El peso (también llamado fuerza de gravedad) es una fuerza omnipresente que actúa en todo momento y debe ser contrarrestada para evitar que un objeto caiga. Definitivamente notas que debes soportar el peso de un objeto pesado empujándolo hacia arriba cuando lo mantienes estacionario, como se ilustra en la Figura\(\PageIndex{1}\) (a). Pero, ¿cómo soportan los objetos inanimados como una mesa el peso de una masa colocada sobre ellos, como se muestra en la Figura\(\PageIndex{1}\) (b)? Cuando la bolsa de comida para perros se coloca sobre la mesa, la mesa en realidad se hunde ligeramente bajo la carga. Esto se notaría si la carga se colocara sobre una mesa de cartas, pero incluso los objetos rígidos se deforman cuando se les aplica una fuerza. A menos que el objeto se deforme más allá de su límite, ejercerá una fuerza restauradora muy parecida a un resorte deformado (o trampolín o tabla de buceo). Cuanto mayor sea la deformación, mayor será la fuerza restauradora. Entonces, cuando la carga se coloca sobre la mesa, la mesa se hunde hasta que la fuerza restauradora llega a ser tan grande como el peso de la carga. En este punto la fuerza externa neta sobre la carga es cero. Esa es la situación cuando la carga está estacionaria sobre la mesa. La mesa se hunde rápidamente, y el pandeo es leve por lo que no lo notamos. Pero es similar a la flacidez de un trampolín cuando subes a él.

Figura\(\PageIndex{1}\): (a) La persona que sostiene la bolsa de alimento para perros debe suministrar una fuerza ascendente\(\boldsymbol{F}_{\text {hand }}\) igual en magnitud y opuesta en dirección al peso del alimento\(w\). (b) La mesa de cartas se hunde cuando se le coloca el alimento para perros, al igual que un trampolín rígido. Las fuerzas elásticas restauradoras en la mesa crecen a medida que se agacha hasta que suministran una fuerza N igual en magnitud y opuesta en dirección al peso de la carga.

Debemos concluir que lo que sea que soporte una carga, sea animada o no, debe suministrar una fuerza ascendente igual al peso de la carga, como suponíamos en algunos de los ejemplos anteriores. La fuerza que soporta una carga es perpendicular a la superficie de contacto entre la carga y su soporte, y esta fuerza se denomina fuerza normal, a menudo indicada con el símbolo N (Por favor, no confunda esto con la abreviatura de newton, la unidad de fuerza, N). La palabra normal significa perpendicular a una superficie. La fuerza normal no siempre es igual al peso del objeto, si hay otras fuerzas que actúan sobre el objeto, o si el objeto está acelerando, de manera que la fuerza neta no sea cero.

La fuerza normal también va por otro nombre, peso aparente. Esto se debe a que todas las fuerzas que sientes, especialmente tu sensación de peso, se atribuyen directamente a fuerzas de contacto, como la fuerza normal. Cuando los astronautas de la NASA flotan sin peso en la Estación Espacial Internacional, su peso real (fuerza gravitacional sobre ellos por la Tierra) no es cero, pero su peso aparente (sensación de peso debido a las fuerzas de contacto) es cero.

Tensión

Una tensión es una fuerza a lo largo de un medio, especialmente una fuerza transportada por un medio flexible, como una cuerda o cable. La palabra “tensión” proviene de una palabra latina que significa “estirar”. No casualmente, los cordones flexibles que transportan las fuerzas musculares a otras partes del cuerpo se llaman tendones. Cualquier conector flexible, como una cuerda, cuerda, cadena, alambre o cable, puede ejercer tirones solo paralelos a su longitud; así, una fuerza transportada por un conector flexible es una tensión con dirección paralela al conector. Es importante entender que la tensión es un tirón en un conector. En contraste, considera la frase: “No se puede empujar una cuerda”. La fuerza de tensión tira hacia afuera a lo largo de los dos extremos de una cuerda.

Considera a una persona sosteniendo una masa sobre una cuerda como se muestra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Cuando un conector perfectamente flexible (uno que no requiere fuerza para doblarlo) como esta cuerda transmite una fuerza T, esa fuerza debe ser paralela a la longitud de la cuerda, como se muestra. El tirón que ejerce tal conector flexible es una tensión. Tenga en cuenta que la cuerda tira con igual fuerza pero en direcciones opuestas en la mano y la masa soportada (descuidando el peso de la cuerda). Este es un ejemplo de la tercera ley de Newton. La cuerda es el medio que lleva las fuerzas iguales y opuestas entre los dos objetos. La tensión en cualquier parte de la cuerda entre la mano y la masa es igual. Una vez que haya determinado la tensión en una ubicación, ha determinado la tensión en todas las ubicaciones a lo largo de la cuerda.

La tensión en la cuerda debe ser igual al peso de la masa soportada, como podemos probar usando la segunda ley de Newton. Si la masa de 5.00-kg en la figura es estacionaria, entonces su aceleración es cero, y así\(\boldsymbol{F}_{\text {net }}=0\). Las únicas fuerzas externas que actúan sobre la masa son su peso\(w\) y la tensión T suministrada por la cuerda. Así,

\[F_{\text {net }}=T-w=0, \nonumber \]

donde T y\(w\) son las magnitudes de la tensión y peso y sus signos indican dirección, con arriba siendo positivos aquí. Así, tal como cabría esperar, la tensión equivale al peso de la masa soportada:

\[T=w=m g. \nonumber \]

Para una masa de 5.00-kg, entonces (descuidando la masa de la cuerda) vemos que

\[T=m g=(5.00 \mathrm{~kg})\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)=49.0 \mathrm{~N}. \nonumber\]

Si cortamos la cuerda e insertamos un resorte, el resorte se extendería una longitud correspondiente a una fuerza de 49.0 N, proporcionando una observación directa y medida de la fuerza de tensión en la cuerda.

Los conectores flexibles se utilizan a menudo para transmitir fuerzas alrededor de las esquinas, como en un sistema de tracción hospitalario, una articulación de dedo o un cable de freno de bicicleta. Si no hay fricción, la tensión se transmite sin disminuir. Solo cambia su dirección, y siempre es paralelo al conector flexible. Esto se ilustra en las figuras\(\PageIndex{3}\) (a) y (b).

Figura\(\PageIndex{3}\): (a) Los tendones en el dedo llevan la fuerza T desde los músculos a otras partes del dedo, generalmente cambiando la dirección de la fuerza, pero no su magnitud (los tendones están relativamente libres de fricción). b) El cable de freno de una bicicleta transporta la tensión T desde el manillar hasta el mecanismo de freno. Nuevamente, se cambia la dirección pero no la magnitud de T.

Figura\(\PageIndex{4}\): A menos que se ejerza una tensión infinita, cualquier conector flexible, como la cadena en la parte inferior de la imagen, se combará bajo su propio peso, dando una curva característica cuando el peso se distribuye uniformemente a lo largo de la longitud, conocida como curva catenaria. Los puentes de suspensión, como el puente Golden Gate que se muestra en esta imagen, son esencialmente conectores flexibles muy pesados. El peso del puente se distribuye uniformemente a lo largo de la longitud de conectores flexibles, generalmente cables, que adquieren la forma característica. (crédito: folleto, Wikimedia Commons)

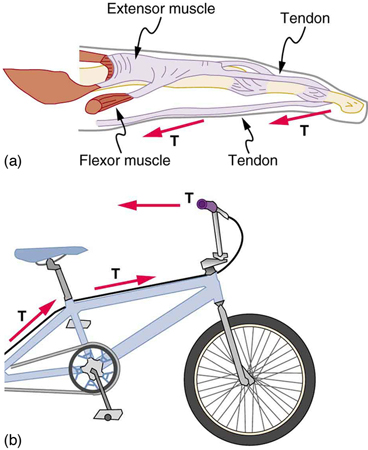
La fuerza y la tensión normales son ejemplos de fuerzas que están determinadas no por una fórmula específica sino por la aplicación de una restricción al estado de movimiento de un cuerpo. En el ejemplo de la bolsa sobre una mesa anterior, la fuerza normal es igual al peso, pues ese es el valor necesario para asegurar que la aceleración de la bolsa sea cero. ¿Qué sucede si el cuerpo experimenta una aceleración distinta de cero? Consideraremos ejemplo a continuación de una persona de pie sobre una báscula (que mide su aparente peso) mientras viajaba en un elevador.

Ejemplo\(\PageIndex{1}\): What Does the Bathroom Scale Read in an Elevator?

La figura\(\PageIndex{5}\) muestra a un hombre de 75.0-kg (peso de aproximadamente 165 lb.) de pie en una báscula de baño en un elevador. Calcular la lectura de la escala: (a) si el elevador acelera hacia arriba a una velocidad de\(1.20 \mathrm{~m} / \mathrm{s}^{2}\), y (b) si el elevador se mueve hacia arriba a una velocidad constante de 1 m/s.

Figura\(\PageIndex{5}\): a) Las diversas fuerzas que actúan cuando una persona se para sobre una báscula de baño en un elevador. Las flechas son aproximadamente correctas para cuando el elevador está acelerando hacia arriba; las flechas rotas representan fuerzas demasiado grandes para ser dibujadas a escala. \(\overrightarrow{\mathbf{T}}\)es la tensión en el cable de soporte,\(\overrightarrow{\mathbf{w}}\) es el peso de la persona,\(\overrightarrow{\mathbf{w}}_{\mathrm{s}}\) es el peso de la báscula,\(\overrightarrow{\mathbf{w}}_{\mathrm{e}}\) es el peso del elevador,\(\overrightarrow{\mathbf{F}}_{\mathrm{s}}\) es la fuerza de la báscula sobre la persona,\(\overrightarrow{\mathbf{F}}_{\mathrm{P}}\) es la fuerza de la persona en la báscula,\(\overrightarrow{\mathbf{F}}_{\mathrm{t}}\) es la fuerza del escala en el piso del elevador, y\(\overrightarrow{\mathbf{N}}\) es la fuerza del piso hacia arriba sobre la báscula. (b) El diagrama de cuerpo libre muestra únicamente las fuerzas externas que actúan sobre el sistema de interés designado —la persona— y es el diagrama que utilizamos para la solución del problema.

Estrategia

Si la escala en reposo es precisa, su lectura es igual\(\overrightarrow{\mathbf{F}}_{\mathrm{P}}\), la magnitud de la fuerza que la persona ejerce hacia abajo sobre ella. La figura\(\PageIndex{5}\) (a) muestra las numerosas fuerzas que actúan sobre el elevador, la báscula y la persona. Hace que este problema unidimensional parezca mucho más formidable que si se elige a la persona para que sea el sistema de interés y se dibuje un diagrama de cuerpo libre, como en la Figura\(\PageIndex{5}\) (b). El análisis del diagrama de cuerpo libre utilizando las leyes de Newton puede producir respuestas tanto a la Figura\(\PageIndex{5}\) (a) como a (b) de este ejemplo, así como a algunas otras preguntas que puedan surgir. Las únicas fuerzas que actúan sobre la persona son su peso\(\overrightarrow{\mathbf{w}}\) y la fuerza ascendente de la báscula\(\overrightarrow{\mathbf{F}}_{\mathrm{s}}\). De acuerdo con la tercera ley de Newton,\(\overrightarrow{\mathbf{F}}_{\mathrm{P}}\) y\(\overrightarrow{\mathbf{F}}_{\mathrm{s}}\) son iguales en magnitud y opuestos en dirección, por lo que necesitamos encontrar F _s para encontrar lo que lee la escala. Podemos hacer esto, como siempre, aplicando la segunda ley de Newton,

\[\overrightarrow{\mathbf{F}}_{\text {net }}=m \overrightarrow{\mathbf{a}}. \nonumber\]

Del diagrama de cuerpo libre, vemos que la fuerza neta\(\overrightarrow{\mathbf{F}}_{\text {net }}\) es la suma de la fuerza de escala\(\overrightarrow{\mathbf{F}}_{\mathrm{s}}\) y el peso\(\overrightarrow{\mathbf{w}}\). Dado que la fuerza de escala y el peso apuntan en direcciones opuestas, en términos de las magnitudes de los vectores,

\[F_{\text {net }}=F_{s}-w=m a. \nonumber\]

Resolver para F _s nos da una ecuación con solo una desconocida:

\[F_{\mathrm{s}}=m a+w, \nonumber\]

o, porque\(w=m g\), simplemente

\[F_{\mathrm{s}}=m a+m g. \nonumber\]

No se hicieron suposiciones sobre la aceleración, por lo que esta solución debería ser válida para una variedad de aceleraciones además de las que se encuentran en esta situación. (Nota: Estamos considerando el caso cuando el elevador está acelerando hacia arriba. Si el elevador está acelerando a la baja, la segunda ley de Newton se vuelve\(F_{s}-w=-m a \).)

Solución

1. Tenemos\(a=1.20 \mathrm{~m} / \mathrm{s}^{2}\), para que

   \[F_{\mathrm{s}}=(75.0 \mathrm{~kg})\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)+(75.0 \mathrm{~kg})\left(1.20 \mathrm{~m} / \mathrm{s}^{2}\right) \nonumber\]

   rindiendo

   \[F_{\mathrm{s}}=825 \mathrm{~N}. \nonumber\]

2. Ahora bien, ¿qué sucede cuando el elevador alcanza una velocidad ascendente constante? ¿La báscula seguirá leyendo más que su peso? Para cualquier velocidad constante (arriba, abajo o estacionaria) la aceleración es cero porque\(a=\frac{\Delta v}{\Delta t}\) y\(\Delta v=0\). Así,

   \[F_{\mathrm{s}}=m a+m g=0+m g \nonumber\]

   o

   \[F_{\mathrm{s}}=(75.0 \mathrm{~kg})\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right), \nonumber\]

   
   que da

   \[F_{\mathrm{s}}=735 \mathrm{~N}. \nonumber\]

Importancia

La lectura de la escala en la Figura\(\PageIndex{5}\) (a) es de aproximadamente 185 lb. ¿Qué habría leído la escala si estuviera estacionario? Como su aceleración sería cero, la fuerza de la báscula sería igual a su peso:

\ [\ begin {reunió}
F_ {\ text {net}} =m a=0=F_ {\ mathrm {s}} -w\\
F_ {\ mathrm {s}} =w=m g\
F_ {\ mathrm {s}} =( 75.0\ mathrm {~kg})\ left (9.80\ mathrm {~m}/\ mathrm {s} ^ {2}\ derecha) =735\ mathrm {~N}.
\ end {reunido}\ nonumber\]

Así, la lectura de la báscula en el elevador es mayor que su peso de 735-N (165-lb.). Esto quiere decir que la báscula está empujando hacia arriba a la persona con una fuerza mayor que su peso, como debe ser para acelerarlo hacia arriba. Claramente, cuanto mayor sea la aceleración del elevador, mayor será la lectura de la báscula, consistente con lo que siente al acelerar rápidamente versus acelerar lentamente los elevadores. En la Figura\(\PageIndex{5}\) (b), la lectura de la escala es 735 N, lo que equivale al peso de la persona. Este es el caso cuando el elevador tiene una velocidad constante: moverse hacia arriba, bajar o estacionarse.

Resumen de la Sección

• Cuando los objetos descansan sobre una superficie, la superficie aplica una fuerza al objeto que soporta el peso del objeto. Esta fuerza de soporte actúa perpendicular a y lejos de la superficie. Se le llama fuerza normal, y también se le conoce con el nombre de “peso aparente”.
• Cuando los objetos descansan sobre una superficie horizontal no acelerada, la magnitud de la fuerza normal es igual al peso del objeto:

  \[N=m g. \nonumber\]

• La fuerza de tracción que actúa a lo largo de un conector flexible estirado, como una cuerda o cable, se llama tensión, T. Cuando una cuerda soporta el peso de un objeto que está en reposo, la tensión en la cuerda es igual al peso del objeto:

  \[T=m g. \nonumber\]

Glosario

fuerza normal

la fuerza que una superficie aplica a un objeto para soportar el peso del objeto; actúa perpendicular a la superficie sobre la que descansa el objeto

peso aparente

sensación de peso debido a las fuerzas de contacto; generalmente lo mismo que la fuerza normal

tensión

la fuerza de tracción que actúa a lo largo de un medio, especialmente un conector flexible estirado, como una cuerda o cable; cuando una cuerda soporta el peso de un objeto, la fuerza sobre el objeto debida a la cuerda se denomina fuerza de tensión