6.4: Energía cinética rotacional

Objetivos de aprendizaje

• Adivina la ecuación para la energía cinética rotacional por analogía.
• Calcular la energía cinética rotacional.

En este módulo, aprenderemos sobre el trabajo y la energía asociada al movimiento rotacional. La figura\(\PageIndex{1}\) muestra a un trabajador que utiliza una muela eléctrica propulsada por un motor. Las chispas están volando, y el ruido y la vibración se crean a medida que las capas de acero se apartan del poste. La piedra sigue girando incluso después de que se apaga el motor, pero finalmente se detiene por fricción. Claramente, el motor tuvo que funcionar para que la piedra giriera. Este trabajo se enfocó en calor, luz, sonido, vibración y considerable energía cinética rotacional.

Figura\(\PageIndex{1}\): El motor trabaja en el giro de la muela, dándole energía cinética rotacional. Esa energía se convierte entonces en calor, luz, sonido y vibración. (crédito: Foto de la Marina de los Estados Unidos por el marinero Zachary David Bell, especialista en comunicación masiva)

En lugar de derivar la fórmula para la energía cinética rotacional calculando el trabajo realizado por torque en un objeto giratorio, simplemente podemos adivinar la fórmula correcta por analogía. Conocemos la energía cinética en movimiento lineal o traslacional\(\mathrm{KE}=\frac{1}{2} m v^{2}\). Podemos encontrar la versión rotacional de la energía cinética reemplazando la masa\(m\) por la versión rotacional de la masa, la inercia\(I\) rotacional y reemplazando la velocidad\(v\) por la velocidad rotacional\(\omega\). La velocidad de rotación se mide en unidades de radianes por segundo. Con estos reemplazos, obtenemos la fórmula para la energía cinética rotacional,

\[\mathrm{KE}_{\mathrm{rot}}=\frac{1}{2} I \omega^{2}. \nonumber \]

La energía cinética rotacional tiene efectos importantes. Los volantes, por ejemplo, se pueden utilizar para almacenar grandes cantidades de energía cinética rotacional en un vehículo, como se ve en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Se han construido vehículos experimentales, como este bus, en los que la energía cinética rotacional se almacena en un volante grande. Cuando el autobús baja una colina, su transmisión convierte su energía potencial gravitacional en\(\mathrm{KE}_{\text {rot }}\). También puede convertir la energía cinética traslacional, cuando el autobús se detiene, en\(\mathrm{KE}_{\text {rot }}\). La energía del volante se puede utilizar entonces para acelerar, subir otra colina, o para evitar que el autobús vaya contra la fricción.

Los pilotos de helicópteros están bastante familiarizados con la energía cinética rotacional Saben, por ejemplo, que se alcanzará un punto de no retorno si permiten que sus palas se desaceleren por debajo de una velocidad angular crítica durante el vuelo. Las palas pierden sustentación, y es imposible conseguir inmediatamente que las cuchillas giren lo suficientemente rápido como para recuperarla. Se debe suministrar energía cinética rotacional a las cuchillas para que giren más rápido, y no se puede suministrar suficiente energía a tiempo para evitar un choque. Debido a las limitaciones de peso, los motores de los helicópteros son demasiado pequeños para suministrar tanto la energía necesaria para la elevación como para reponer la energía cinética de rotación de las palas una vez que se han ralentizado. La energía cinética rotacional se pone en ellos antes del despegue y no se debe permitir que caiga por debajo de este nivel crucial. Una forma posible de evitar un choque es utilizar la energía potencial gravitacional del helicóptero para reponer la energía cinética rotacional de las palas al perder altitud y alinear las palas para que el helicóptero gire en el descenso. Por supuesto, si la altitud del helicóptero es demasiado baja, entonces no hay tiempo suficiente para que la pala recupere sustentación antes de llegar al suelo.

Ejemplo\(\PageIndex{1}\): Calculating Helicopter Energies

Un típico helicóptero de rescate pequeño, similar al de la Figura\(\PageIndex{3}\), tiene cuatro palas, cada una mide 4.00 m de largo y tiene una masa de 50.0 kg. Las cuchillas pueden aproximarse como varillas delgadas que giran alrededor de un extremo de un eje perpendicular a su longitud. El helicóptero tiene una masa total cargada de 1000 kg. (a) Calcular la energía cinética rotacional en las palas cuando giran a 300 rpm. b) Calcular la energía cinética traslacional del helicóptero cuando vuela a 20.0 m/s, y compararla con la energía rotacional en las palas. c) ¿A qué altura podría elevarse el helicóptero si se pudiera utilizar toda la energía cinética rotacional para levantarlo?

Estrategia

Las energías cinéticas rotacionales y traslacionales se pueden calcular a partir de sus definiciones. La última parte del problema se relaciona con la idea de que la energía puede cambiar de forma, en este caso de energía cinética rotacional a energía potencial gravitacional.

Solución para (a)

La energía cinética rotacional es

\[\mathrm{KE}_{\mathrm{rot}}=\frac{1}{2} I \omega^{2}. \nonumber\]

Debemos convertir la velocidad angular a radianes por segundo y calcular el momento de inercia antes de poder encontrarla\(\mathrm{KE}_{\mathrm{rot}}\). La velocidad angular\(\omega\) es

\[\omega=\frac{300 \mathrm{rev}}{1.00 \mathrm{~min}} \cdot \frac{2 \pi \mathrm{rad}}{1 \mathrm{rev}} \cdot \frac{1.00 \mathrm{~min}}{60.0 \mathrm{~s}}=31.4 \frac{\mathrm{rad}}{\mathrm{s}}. \nonumber\]

El momento de inercia de una pala será el de una varilla delgada girada alrededor de su extremo,\(I_{\mathrm{rod}}=\frac{1}{3} M \ell^{2}\). El total\(I\) es cuatro veces este momento de inercia, porque hay cuatro palas. Así,

\[I=4 \frac{M \ell^{2}}{3}=4 \times \frac{(50.0 \mathrm{~kg})(4.00 \mathrm{~m})^{2}}{3}=1067 \mathrm{~kg} \cdot \mathrm{m}^{2}. \nonumber\]

Entrar\(\omega\) y\(I\) entrar en la expresión de energía cinética rotacional da

\ [\ begin {alineado}
\ mathrm {KE} _ {\ mathrm {rot}} &=0.5\ izquierda (1067\ mathrm {~kg}\ cdot\ mathrm {m} ^ {2}\ derecha) (31.4\ mathrm {rad}/\ mathrm {s}) ^ {2}\\
&=5.26\ veces 10^ {5}\ mathrm {~J}
\ end {alineado}\ nonumber\]

Solución para (b)

Introduciendo los valores dados de masa y velocidad en la fórmula para la energía cinética traslacional, obtenemos

\[\mathrm{KE}_{\text {trans }}=\frac{1}{2} m v^{2}=(0.5)(1000 \mathrm{~kg})(20.0 \mathrm{~m} / \mathrm{s})^{2}=2.00 \times 10^{5} \mathrm{~J}. \nonumber\]

Para comparar las energías cinéticas, tomamos la relación de energía cinética traslacional a energía cinética rotacional. Esta relación es

\[\frac{2.00 \times 10^{5} \mathrm{~J}}{5.26 \times 10^{5} \mathrm{~J}}=0.380. \nonumber\]

Solución para (c)

A la altura máxima, toda la energía cinética rotacional se habrá convertido en energía gravitacional. Para encontrar esta altura, equiparamos esas dos energías:

\[\mathrm{KE}_{\text {rot }}=\mathrm{PE}_{\text {grav }} \nonumber\]

o

\[\frac{1}{2} I \omega^{2}=m g h. \nonumber\]

Ahora resolvemos\(h\) y sustituimos valores conocidos en la ecuación resultante

\[h=\frac{\frac{1}{2} I \omega^{2}}{m g}=\frac{5.26 \times 10^{5} \mathrm{~J}}{(1000 \mathrm{~kg})\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)}=53.7 \mathrm{~m}. \nonumber\]

Discusión

La relación de energía de traslación a energía cinética rotacional es de solo 0.380. Esta proporción nos dice que la mayor parte de la energía cinética del helicóptero está en sus palas giratorias, algo que probablemente no sospecharías. La altura de 53.7 m a la que podría elevarse el helicóptero con la energía cinética rotacional también es impresionante, enfatizando nuevamente la cantidad de energía cinética rotacional en las palas.

Figura\(\PageIndex{3}\): La primera imagen muestra cómo los helicópteros almacenan grandes cantidades de energía cinética rotacional en sus palas. Esta energía debe ser puesta en las cuchillas antes del despegue y mantenida hasta el final del vuelo. Los motores no tienen suficiente potencia para proporcionar simultáneamente elevación y poner energía rotacional significativa en las palas. La segunda imagen muestra un helicóptero del Servicio de Helicópteros de Rescate Westpac de Auckland. Se han salvado más de 50 mil vidas desde que sus operaciones comenzaron en 1973. Aquí se muestra una operación de rescate acuático. (crédito: 111 Emergency, Flickr)

¿Qué tan espesa es la sopa? O ¿por qué no todos los objetos ruedan cuesta abajo al mismo ritmo?

Uno de los controles de calidad en una fábrica de sopa de tomate consiste en enrollar latas llenas por una rampa. Si ruedan demasiado rápido, la sopa es demasiado delgada. ¿Por qué las latas de idéntico tamaño y masa deben rodar por una pendiente a diferentes tasas? Y ¿por qué la sopa más espesa debería rodar la más lenta?

La forma más fácil de responder a estas preguntas es considerar la energía. Supongamos que cada lata comienza por la rampa desde el descanso. Cada lata a partir del reposo significa que cada uno comienza con la misma energía potencial gravitacional\(\mathrm{PE}_{\text {grav }}\), que se convierte completamente en KE, siempre que cada rueda sin resbalar. KE, sin embargo, puede tomar la forma de\(\mathrm{KE}_{\text {trans }}\) o\(\mathrm{KE}_{\text {rot }}\), y KE total es la suma de los dos. Si una lata rueda por una rampa, pone parte de su energía en rotación, dejando menos para la traslación. Así, la lata va más lenta de lo que lo haría si se deslizara hacia abajo. Además, la sopa fina no gira, mientras que la sopa espesa sí, porque se pega a la lata. La sopa espesa pone así en rotación más energía potencial gravitacional original de la lata que la sopa delgada, y la lata rueda más lentamente, como se ve en la Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\): Tres latas de sopa con masas idénticas corren por una pendiente. La primera lata tiene un recubrimiento de baja fricción y no rueda sino que simplemente se desliza por la pendiente. Gana porque convierte toda su PE en KE traslacional. Tanto la segunda como la tercera latas ruedan por la pendiente sin resbalar. La segunda lata contiene sopa fina y viene en segundo lugar porque parte de su PE inicial entra en la rotación de la lata (pero no la sopa delgada). La tercera lata contiene sopa espesa. Viene en tercer lugar porque la sopa gira junto con la lata, tomando aún más del PE inicial para KE rotacional, dejando menos para KE traslacional.

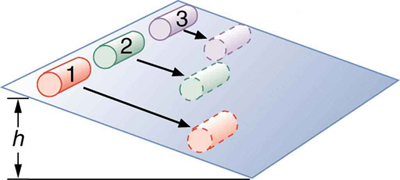
Asumiendo que no hay pérdidas por fricción, solo hay una fuerza trabajando: la gravedad. Por lo tanto, el trabajo total realizado es el cambio en la energía cinética. A medida que las latas comienzan a moverse, la energía potencial se está convirtiendo en energía cinética. Conservación de energía da

\[\mathrm{PE}_{\mathrm{i}}=\mathrm{KE}_{\mathrm{f}}. \nonumber \]

Más específicamente,

\[\mathrm{PE}_{\text {grav }}=\mathrm{KE}_{\text {trans }}+\mathrm{KE}_{\mathrm{rot}} \nonumber \]

o

\[m g h=\frac{1}{2} m v^{2}+\frac{1}{2} I \omega^{2}. \nonumber \]

Entonces, la inicial\(mgh\) se divide entre energía cinética traslacional y energía cinética rotacional; y cuanto mayor\(I\) es, menos energía entra en traslación. Si la lata se desliza hacia abajo sin fricción, entonces\(ω=0\) y toda la energía entra en traslación; así, la lata va más rápido.

EXPERIMENTO PARA LLEVAR A CASA

Localice varias latas cada una que contenga un tipo diferente de alimento (por ejemplo, sopa enlatada con diferentes tipos de sopa). En primer lugar, predecir cuál puede ganará la carrera por un plano inclinado y explique por qué. Vea si su predicción es correcta. Se puede obtener un buen contraste entre un concentrado espeso de sopa (por ejemplo, crema condensada de champiñones) y una sopa fina (por ejemplo, sopa de fideos de pollo). Si te sientes aventurero, prueba otros alimentos, como el maíz enlatado o los guisantes; intenta predecir cómo se compararían estos con, por ejemplo, la lata de crema condensada de hongos en la carrera por un plano inclinado.

Ejemplo\(\PageIndex{2}\): Calculating the Speed of a Cylinder Rolling Down an Incline

Calcule la velocidad final de un cilindro sólido que rueda por una inclinación de 2.00-m de altura. El cilindro parte del reposo, tiene una masa de 0.750 kg, y tiene un radio de 4.00 cm.

Estrategia

Podemos resolver para la velocidad final usando la conservación de energía, pero primero debemos expresar cantidades rotacionales en términos de cantidades de traslación para terminar con v como el único desconocido.

Solución

La conservación de la energía para esta situación está escrita como se describió anteriormente:

\[m g h=\frac{1}{2} m v^{2}+\frac{1}{2} I \omega^{2}. \nonumber\]

Antes de que podamos resolver por\(v\), debemos buscar una expresión\(I\) para un disco sólido:\(I_{\text {disk }}=\frac{1}{2} M \ell^{2}\). Porque\(v\) y\(\omega\) están relacionados (tenga en cuenta aquí que el cilindro está rodando sin deslizarse), también debemos sustituir la relación\(\omega=v / R\) en la expresión. Estas sustituciones producen

\[m g h=\frac{1}{2} m v^{2}+\frac{1}{2}\left(\frac{1}{2} m R^{2}\right)\left(\frac{v^{2}}{R^{2}}\right). \nonumber\]

Curiosamente, el radio\(R\) y la masa del cilindro\(m\) cancelan, cediendo

\[g h=\frac{1}{2} v^{2}+\frac{1}{4} v^{2}=\frac{3}{4} v^{2}. \nonumber\]

Resolviendo algebraicamente, la ecuación para la velocidad final\(v\) da

\[v=\left(\frac{4 g h}{3}\right)^{1 / 2}. \nonumber\]

Sustituir valores conocidos en los rendimientos de expresión resultantes

\[v=\left[\frac{4\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)(2.00 \mathrm{~m})}{3}\right]^{1 / 2}=5.11 \mathrm{~m} / \mathrm{s}. \nonumber\]

Discusión

Porque\(m\) y\(R\) cancelar, el resultado\(v=\left(\frac{4}{3} g h\right)^{1 / 2}\) es válido para cualquier cilindro sólido, lo que implica que todos los cilindros sólidos rodarán por una inclinación a la misma velocidad independientemente de sus masas y tamaños. (Rodando cilindros hacia abajo inclinaciones es lo que Galileo realmente hizo para demostrar que los objetos caen al mismo ritmo independientemente de la masa). Tenga en cuenta que si el cilindro se deslizaba sin fricción por la pendiente sin rodar, entonces toda la energía potencial gravitacional entraría en energía cinética traslacional. Así,\(\frac{1}{2} m v^{2}=m g h\) y\(v=(2 g h)^{1 / 2}\), que es 22% mayor que\((4 g h / 3)^{1 / 2}\). Es decir, el cilindro iría más rápido en la parte inferior.

Ejercicio\(\PageIndex{1}\)

Analogía de la Energía Cinética Rotacional y Traslacional

¿La energía cinética rotacional es completamente análoga a la energía cinética de traslación ¿Cuáles, si las hay, son sus diferencias? Dar un ejemplo de cada tipo de energía cinética.

Responder

Sí, la energía cinética rotacional y traslacional son análogos exactos. Ambos son la energía del movimiento involucrada con el movimiento coordinado (no aleatorio) de masa en relación con algún marco de referencia. La única diferencia entre la energía cinética rotacional y traslacional es que la traslación es movimiento en línea recta mientras que la rotación no lo es. Un ejemplo de energía cinética tanto cinética como traslacional se encuentra en un neumático de bicicleta mientras se conduce por un carril bici. El movimiento rotacional del neumático significa que tiene energía cinética rotacional, mientras que el movimiento de la bicicleta a lo largo de la trayectoria significa que el neumático también tiene energía cinética de traslación. Si tuvieras que levantar la rueda delantera de la bicicleta y girarla mientras la bicicleta está estacionaria, entonces la rueda solo tendría energía cinética rotacional con relación a la Tierra.

Resumen de la Sección

• La energía cinética rotacional\(\mathrm{KE}_{\text {rot }}\) para un objeto con un momento de inercia\(I\) y una velocidad angular\(\omega\) viene dada por

  \[\mathrm{KE}_{\mathrm{rot}}=\frac{1}{2} I \omega^{2}. \nonumber\]

• Los helicópteros almacenan grandes cantidades de energía cinética rotacional en sus palas. Esta energía debe ser puesta en las cuchillas antes del despegue y mantenida hasta el final del vuelo. Los motores no tienen suficiente potencia para proporcionar simultáneamente elevación y poner energía rotacional significativa en las palas.
• El trabajo y la energía en el movimiento rotacional son completamente análogos al trabajo y la energía en el movimiento traslacional.

Glosario

energía cinética rotacional

la energía cinética debida a la rotación de un objeto. Esto es parte de su energía cinética total