6.6: Efectos Giroscópicos- Aspectos Vectoriales del Momentum Angular
- Page ID
- 133761
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Describa la regla de la derecha para encontrar la dirección de la velocidad angular, el momento y el par.
- Explicar el efecto giroscópico.
- Estudia cómo la Tierra actúa como un giroscopio gigantesco.
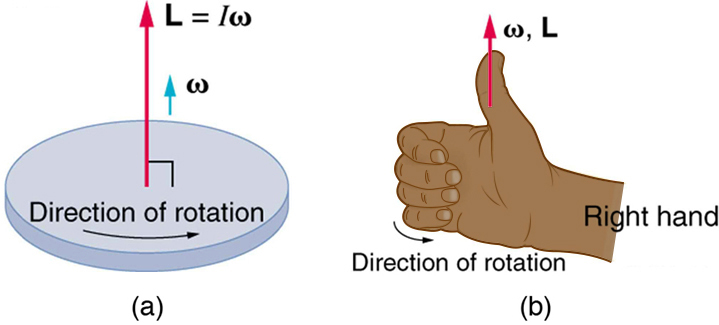
El momento angular es un vector y, por lo tanto, tiene dirección así como magnitud. El par afecta tanto la dirección como la magnitud del momento angular. ¿Cuál es la dirección del momento angular de un objeto giratorio como el disco en la Figura\(\PageIndex{1}\)? La figura muestra la regla de la derecha utilizada para encontrar la dirección tanto del momento angular como de la velocidad angular. Ambos\(\mathbf{L}\) y\(\boldsymbol{\omega}\) son vectores, cada uno tiene dirección y magnitud. Ambos pueden ser representados por flechas. La regla de la derecha define ambos para ser perpendiculares al plano de rotación en la dirección mostrada. Debido a que el momento angular está relacionado con la velocidad angular por\(\mathbf{L}=I \boldsymbol{\omega}\), la dirección de\(\mathbf{L}\) es la misma que la dirección de\(\boldsymbol{\omega}\). Observe en la figura que ambos apuntan a lo largo del eje de rotación.
Ahora, recuerde que el par cambia el momento angular expresado por
\[\text { net } \boldsymbol{\tau}=\frac{\Delta \mathbf{L}}{\Delta t} \nonumber \]
Esta ecuación significa que la dirección de\(\Delta \mathbf{L}\) es la misma que la dirección del par\(\boldsymbol{\tau}\) que la crea. Este resultado se ilustra en la Figura\(\PageIndex{2}\), que muestra la dirección del par y el momento angular que crea.
Consideremos ahora una rueda de bicicleta con un par de asas unidas a ella, como se muestra en la Figura\(\PageIndex{3}\). (Este dispositivo es popular en las demostraciones entre los físicos, porque hace cosas inesperadas). Con la rueda girando como se muestra, su momento angular está a la izquierda de la mujer. Supongamos que la persona que sostiene la rueda intenta girarla como en la figura. Su expectativa natural es que la rueda gire en la dirección en la que la empuja, pero lo que sucede es bastante diferente. Las fuerzas ejercidas crean un par que es horizontal hacia la persona, como se muestra en la Figura\(\PageIndex{3}\) (a). Este par crea un cambio en el momento angular\(\mathbf{L}\) en la misma dirección, perpendicular al momento angular original\(\mathbf{L}\), cambiando así la dirección de\(\mathbf{L}\) pero no la magnitud de\(\mathbf{L}\). La figura\(\PageIndex{3}\) muestra cómo\(\Delta \mathbf{L}\) y\(\mathbf{L}\) sumar, dando un nuevo impulso angular con dirección que se inclina más hacia la persona que antes. El eje de la rueda se ha movido así perpendicular a las fuerzas ejercidas sobre ella, en lugar de en la dirección esperada.

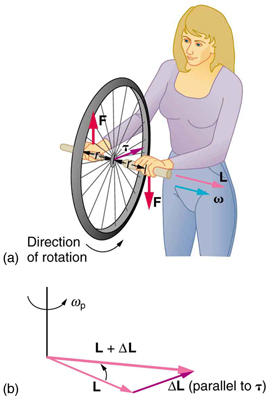
Esta misma lógica explica el comportamiento de los giroscopios. La figura\(\PageIndex{4}\) muestra las dos fuerzas que actúan sobre un giroscopio giratorio. El par producido es perpendicular al momento angular, por lo que se cambia la dirección del momento angular pero no su magnitud, como resultado del cambio en el momento angular producido por el par. Este tipo de movimiento se llama precesión, y decimos que el giroscopio precede alrededor de un eje vertical, ya que el par siempre es horizontal y perpendicular a\(\mathbf{L}\). Si el giroscopio no está girando, adquiere el momento angular inicial en la dirección del torque (\(\mathbf{L}=\Delta \mathbf{L}\)) y el cambio de momento angular debido al par continúa sumando en la misma dirección, haciendo que el giroscopio gire alrededor de un eje horizontal, cayendo justo como esperaríamos.
La Tierra misma actúa como un giroscopio gigantesco. Su momento angular es a lo largo de su eje y apunta a Polaris, la Estrella del Norte. Pero la Tierra está lentamente precediendo (una vez cada 26 mil años) debido al par del Sol y la Luna en su forma no esférica.

Ejercicio\(\PageIndex{1}\)
La energía cinética rotacional se asocia con el momento angular? ¿Significa eso que la energía cinética rotacional es un vector?
- Contestar
-
No, la energía es siempre un escalar, ya sea que el movimiento esté involucrado o no. Ninguna forma de energía tiene una dirección en el espacio y se puede ver que la energía cinética rotacional no depende de la dirección del movimiento así como la energía cinética lineal es independiente de la dirección del movimiento.
Resumen de la Sección
- El par es perpendicular al plano formado por\(r\) y\(\mathbf{F}\) y es la dirección que apuntaría tu pulgar derecho si rizas los dedos de tu mano derecha en la dirección de\(\mathbf{F}\). La dirección del par es, por lo tanto, la misma que la del cambio en el momento angular que produce.
- El giroscopio precede alrededor de un eje vertical, ya que el par es siempre horizontal y perpendicular a\(\mathbf{L}\). Si el giroscopio no está girando, adquiere un impulso angular en la dirección del par (\(\mathbf{L}=\Delta \mathbf{L}\)), y gira alrededor de un eje horizontal, cayendo justo como esperaríamos.
- La Tierra misma actúa como un giroscopio gigantesco. Su momento angular es a lo largo de su eje y apunta a Polaris, la Estrella del Norte.
Glosario
- precesión
- un tipo de movimiento que experimenta un objeto que posee un momento angular, ya que se aplica un par perpendicular a la dirección del momento angular, haciendo que la dirección del momento angular cambie; el movimiento de oscilación circular trazado por una parte superior circular ligeramente inclinada es un ejemplo
- regla de la mano derecha
- dirección de la velocidad angular\(\omega\) y momento angular L en el que el pulgar de tu mano derecha apunta cuando rizas tus dedos en la dirección de rotación del disco


