11.9: Formación de Imagen por Lentes

Objetivos de aprendizaje

• Enumere las reglas para el seguimiento de rayos para lentes delgadas.
• Ilustrar la formación de imágenes utilizando la técnica de rastreo de rayos.
• Determinar la potencia de una lente dada la distancia focal.

Las lentes se encuentran en una gran variedad de instrumentos ópticos, que van desde una simple lupa hasta el ojo hasta el lente de zoom de una cámara. En esta sección, utilizaremos la ley de la refracción para explorar las propiedades de las lentes y cómo forman las imágenes.

La palabra lente deriva de la palabra latina para frijol de lenteja, cuya forma es similar a la lente convexa en la Figura\(\PageIndex{1}\). La lente convexa mostrada ha sido conformada de manera que todos los rayos de luz que entran en ella paralelos a su eje se cruzan entre sí en un solo punto en el lado opuesto de la lente. (El eje se define como una línea normal a la lente en su centro, como se muestra en la Figura)\(\PageIndex{1}\). Tal lente se llama lente convergente (o convexa) por el efecto convergente que tiene sobre los rayos de luz. Se muestra una vista ampliada de la trayectoria de un rayo a través de la lente, para ilustrar cómo el rayo cambia de dirección tanto a medida que entra como a medida que sale de la lente. Dado que el índice de refracción de la lente es mayor que el del aire, el rayo se mueve hacia la perpendicular a medida que entra y se aleja de la perpendicular a medida que sale. (Esto es conforme a la ley de la refracción.) Debido a la forma de la lente, la luz se dobla hacia el eje en ambas superficies. El punto en el que se cruzan los rayos se define como el punto focal F de la lente. La distancia desde el centro de la lente hasta su punto focal se define como la distancia focal\(f\) de la lente. La figura\(\PageIndex{2}\) muestra cómo una lente convergente, como la de una lupa, puede converger los rayos de luz casi paralelos del sol a una pequeña mancha.

Figura\(\PageIndex{1}\): Los rayos de luz que entran en una lente convergente paralela a su eje convergen en su punto focal F. (El rayo 2 se encuentra en el eje de la lente.) La distancia desde el centro de la lente hasta el punto focal es la distancia focal de la lente\(f\). Una vista ampliada de la trayectoria tomada por el rayo 1 muestra las perpendiculares y los ángulos de incidencia y refracción en ambas superficies.

Definición: Lente convergente o convexa

La lente en la que los rayos de luz que entran en ella paralelos a su eje se cruzan entre sí en un solo punto del lado opuesto con un efecto convergente se denomina lente convergente.

Definición: PUNTO FOCAL F

El punto en el que se cruzan los rayos de luz se llama punto focal F de la lente.

Definición: LARGO FOCAL\(f\)

La distancia desde el centro de la lente hasta su punto focal se denomina distancia focal\(f\).

Figura\(\PageIndex{2}\): La luz solar enfocada por una lupa convergente puede quemar papel. Los rayos de luz del sol son casi paralelos y cruzan en el punto focal de la lente. Cuanto más potente sea la lente, más cerca de la lente cruzarán los rayos.

Cuanto mayor efecto tenga una lente sobre los rayos de luz, más potente se dice que es. Por ejemplo, una potente lente convergente enfocará los rayos de luz paralelos más cerca de sí mismo y tendrá una distancia focal más pequeña que una lente débil. La luz también se enfocará en un punto más pequeño e intenso para obtener una lente más potente. La potencia\(P\) de una lente se define como la inversa de su distancia focal. En forma de ecuación, esto es

\[P=\frac{1}{f}. \nonumber \]

Definición: POWER\(P\)

La potencia\(P\) de una lente se define como la inversa de su distancia focal. En forma de ecuación, esto es

\[P=\frac{1}{f}. \nonumber\]

donde\(f\) está la distancia focal de la lente, la cual debe ser dada en metros (y no cm o mm). La potencia de una lente P tiene las dioptrías unitarias (D), siempre que la distancia focal se dé en metros. Es decir,\(1 ~\mathrm{D}=1 / \mathrm{m}\), o\(1 \mathrm{~m}^{-1}\). (Tenga en cuenta que esta potencia (potencia óptica, en realidad) no es lo mismo que la potencia en vatios. Es un concepto relacionado con el efecto de los dispositivos ópticos sobre la luz.) Los optometristas prescriben gafas comunes y lentes de contacto en unidades de dioptrías.

Ejemplo\(\PageIndex{1}\): What is the Power of a Common Magnifying Glass?

Supongamos que sacas una lupa en un día soleado y encuentras que concentra la luz solar en una pequeña mancha a 8.00 cm de distancia de la lente. ¿Cuál es la distancia focal y la potencia de la lente?

Estrategia

La situación aquí es la misma que las que se muestran en la Figura\(\PageIndex{1}\) y la Figura\(\PageIndex{2}\). El Sol está tan lejos que los rayos del Sol son casi paralelos cuando llegan a la Tierra. La lupa es una lente convexa (o convergente), enfocando los rayos casi paralelos de la luz solar. Así, la distancia focal de la lente es la distancia desde la lente hasta el punto, y su potencia es la inversa de esta distancia (en m).

Solución

La distancia focal de la lente es la distancia desde el centro de la lente hasta el punto, dado que es de 8.00 cm. Por lo tanto,

\[f=8.00 \mathrm{~cm}. \nonumber\]

Para encontrar la potencia de la lente, primero debemos convertir la distancia focal a metros; luego, sustituimos este valor en la ecuación por potencia. Esto da

\[P=\frac{1}{f}=\frac{1}{0.0800 \mathrm{~m}}=12.5 ~\mathrm{D}. \nonumber\]

Discusión

Esta es una lente relativamente potente. La potencia de una lente en dioptrías no debe confundirse con el concepto familiar de potencia en vatios. Es un hecho lamentable que la palabra “poder” se utilice para dos conceptos completamente diferentes. Si examina una receta para anteojos, notará los poderes de lente dados en las dioptrías. Si examina la etiqueta en un motor, notará la tasa de consumo de energía dada como una potencia en vatios.

La figura\(\PageIndex{3}\) muestra una lente cóncava y el efecto que tiene sobre los rayos de luz que la ingresan paralelos a su eje (la trayectoria tomada por el rayo 2 en la figura es el eje de la lente). La lente cóncava es una lente divergente, ya que hace que los rayos de luz se doblen (diverjan) de su eje. En este caso, la lente ha sido conformada de manera que todos los rayos de luz que entran en ella paralelos a su eje parecen originarse desde un mismo punto\(F\),, definido como el punto focal de una lente divergente. La distancia desde el centro de la lente hasta el punto focal se llama de nuevo la distancia focal\(f\) de la lente. Tenga en cuenta que la distancia focal y la potencia de una lente divergente se definen como negativas. Por ejemplo, si la distancia a\(F\) en la Figura\(\PageIndex{3}\) es de 5.00 cm, entonces la distancia focal es\(f=-5.00 \mathrm{~cm}\) y la potencia de la lente es\(P=-20 ~\mathrm{D}\). En la figura se muestra una vista ampliada de la trayectoria de un rayo a través de la lente para ilustrar cómo la forma de la lente, junto con la ley de refracción, hace que el rayo siga su trayectoria particular y sea divergido.

Figura\(\PageIndex{3}\): Los rayos de luz que entran en una lente divergente paralela a su eje son divergentes, y todos parecen originarse en su punto focal\(F\). Las líneas discontinuas no son rayos, indican las direcciones de las que parecen provenir los rayos. La distancia focal\(f\) de una lente divergente es negativa. Una vista ampliada de la trayectoria tomada por el rayo 1 muestra las perpendiculares y los ángulos de incidencia y refracción en ambas superficies.

Definición: LENTE DIVERGENTE

Una lente que hace que los rayos de luz se doblen alejándose de su eje se denomina lente divergente.

Como se señaló en la discusión inicial de la ley de la refracción, los caminos de los rayos de luz son exactamente reversibles. Esto significa que la dirección de las flechas podría invertirse para todos los rayos de la Figura\(\PageIndex{1}\) y la Figura\(\PageIndex{3}\). Por ejemplo, si se coloca una fuente de luz puntual en el punto focal de una lente convexa, como se muestra en la Figura\(\PageIndex{4}\), los rayos de luz paralelos emergen del otro lado.

Figura\(\PageIndex{4}\): Una pequeña fuente de luz, como un filamento de bombilla, colocada en el punto focal de una lente convexa, da como resultado rayos de luz paralelos que emergen del otro lado. Los caminos son exactamente los inversos de los que se muestran en la Figura\(\PageIndex{1}\). Esta técnica se utiliza en faros y a veces en semáforos para producir un haz de luz direccional a partir de una fuente que emite luz en todas las direcciones.

Ray Tracing y Lentes Delgadas

El trazado de rayos es la técnica de determinar o seguir (trazar) los caminos que toman los rayos de luz. Para los rayos que pasan por la materia, se utiliza la ley de la refracción para trazar los caminos. Aquí utilizamos el trazado de rayos para ayudarnos a comprender la acción de las lentes en situaciones que van desde la formación de imágenes en película hasta la ampliación de letra pequeña y la corrección de la miopía. Si bien el trazado de rayos para lentes complicados, como los que se encuentran en cámaras sofisticadas, puede requerir técnicas informáticas, existe un conjunto de reglas simples para rastrear los rayos a través de lentes delgadas. Una lente delgada se define como aquella cuyo espesor permite que los rayos se refracten, como se ilustra en la Figura\(\PageIndex{1}\), pero no permite propiedades como dispersión y aberraciones. Una lente delgada ideal tiene dos superficies refractantes pero la lente es lo suficientemente delgada como para asumir que los rayos de luz se doblan solo una vez. Una lente simétrica delgada tiene dos puntos focales, uno a cada lado y ambos a la misma distancia de la lente. (Ver Figura\(\PageIndex{5}\).) Otra característica importante de una lente delgada es que los rayos de luz a través de su centro son desviados en una cantidad insignificante, como se ve en la Figura\(\PageIndex{6}\).

Definición: LENTE FINA

Una lente delgada se define como aquella cuyo espesor permite que los rayos se refracten pero no permita propiedades como dispersión y aberraciones.

EXPERIMENTO PARA LLEGAR A CASA: UNA VISITA AL ÓPTICO

Mira a través de tus anteojos (o los de un amigo) hacia atrás y hacia adelante y comenta si actúan como lentes delgadas.

Figura\(\PageIndex{5}\): Las lentes delgadas tienen la misma distancia focal en cada lado. a) Rayos de luz paralelos que ingresan a una lente convergente desde la cruz derecha en su punto focal a la izquierda. b) Los rayos de luz paralelos que ingresan a una lente divergente desde la derecha parecen provenir del punto focal de la derecha.

Figura\(\PageIndex{6}\): El rayo de luz a través del centro de una lente delgada se desvía en una cantidad insignificante y se supone que emerge paralelo a su trayectoria original (mostrada como una línea sombreada).

Usando papel, lápiz y un borde recto, el trazado de rayos puede describir con precisión el funcionamiento de una lente. Las reglas para el trazado de rayos para lentes delgadas se basan en las ilustraciones ya discutidas:

• Rayo principal 1: un rayo que entra en una lente convergente paralela a su eje pasa por el punto focal F de la lente en el otro lado (ver los rayos 1 y 3 en la figura\(\PageIndex{1}\)); un rayo que entra en una lente divergente paralela a su eje parece provenir del punto focal F (ver rayos 1 y 3 en Figura\(\PageIndex{3}\))
• Rayo principal 2: un rayo que pasa por el centro de una lente convergente o divergente no cambia de dirección (ver Figura\(\PageIndex{6}\), y ver rayo 2 en Figura\(\PageIndex{1}\) y Figura\(\PageIndex{3}\))
• Rayo principal 3: un rayo que entra en una lente convergente a través de su punto focal sale paralelo a su eje (el reverso de los rayos 1 y 3 en la Figura\(\PageIndex{1}\)); un rayo que entra en una lente divergente dirigiéndose hacia el punto focal en el lado opuesto sale paralelo al eje (el reverso de rayos 1 y 3 en la Figura\(\PageIndex{3}\)). El tercer rayo principal es opcional y puede usarse para verificar la precisión de la ubicación de la imagen.

Formación de Imagen por Lentes Delgadas

En algunas circunstancias, una lente forma una imagen obvia, como cuando un proyector de películas proyecta una imagen sobre una pantalla. En otros casos, la imagen es menos obvia. ¿Dónde, por ejemplo, está la imagen formada por anteojos? Utilizaremos el trazado de rayos para lentes delgadas para ilustrar cómo forman las imágenes, y desarrollaremos ecuaciones para describir cuantitativamente la formación de imágenes.

Considere un objeto a cierta distancia de una lente convergente, como se muestra en la Figura\(\PageIndex{7}\). Para encontrar la ubicación y el tamaño de la imagen formada, trazamos los caminos de los rayos principales originados desde un punto sobre el objeto, en este caso la parte superior de la cabeza de la persona. La figura muestra los tres rayos principales desde la parte superior del objeto como se describió anteriormente. (Tenga en cuenta que hay muchos rayos de luz que salen de este punto yendo en muchas direcciones, pero nos concentramos en los tres rayos principales que pueden ser trazados por reglas simples.) El primer rayo es aquel que ingresa a la lente paralelo a su eje y pasa por el punto focal del otro lado (Rayo Principal 1). El segundo rayo pasa por el centro de la lente sin cambiar de dirección (Rayo Principal 2). El tercer rayo pasa a través del punto focal más cercano en su camino hacia la lente y deja la lente paralela a su eje (Rayo Principal 3). Si se dibujan correctamente, los tres rayos se cruzan en el mismo punto del otro lado de la lente. En este punto se ubica la imagen de la parte superior de la cabeza de la persona. Todos los rayos, incluidos los que no son rayos principales, que provienen del mismo punto en la parte superior de la cabeza de la persona son refractados de tal manera que crucen en el punto que se muestra; los rayos principales son los que utilizamos para encontrar este punto. Rayos de otro punto sobre el objeto, como la hebilla de su cinturón, también se cruzarán en otro punto común, formando una imagen completa, como se muestra. Si bien se trazan tres rayos en la Figura\(\PageIndex{7}\), solo son necesarios dos para ubicar la imagen. Antes de aplicar el trazado de rayos a otras situaciones, consideremos con más detalle el ejemplo que se muestra\(\PageIndex{7}\) en la Figura.

Figura\(\PageIndex{7}\): El trazado de rayos se utiliza para localizar la imagen formada por una lente. Se trazan los rayos que se originan desde el mismo punto sobre el objeto; los tres rayos elegidos siguen cada uno una de las reglas para el trazado de rayos, de manera que sus caminos son fáciles de determinar. La imagen se ubica en el punto donde se cruzan los rayos. En este caso, se forma una imagen real, una que se puede proyectar en una pantalla.

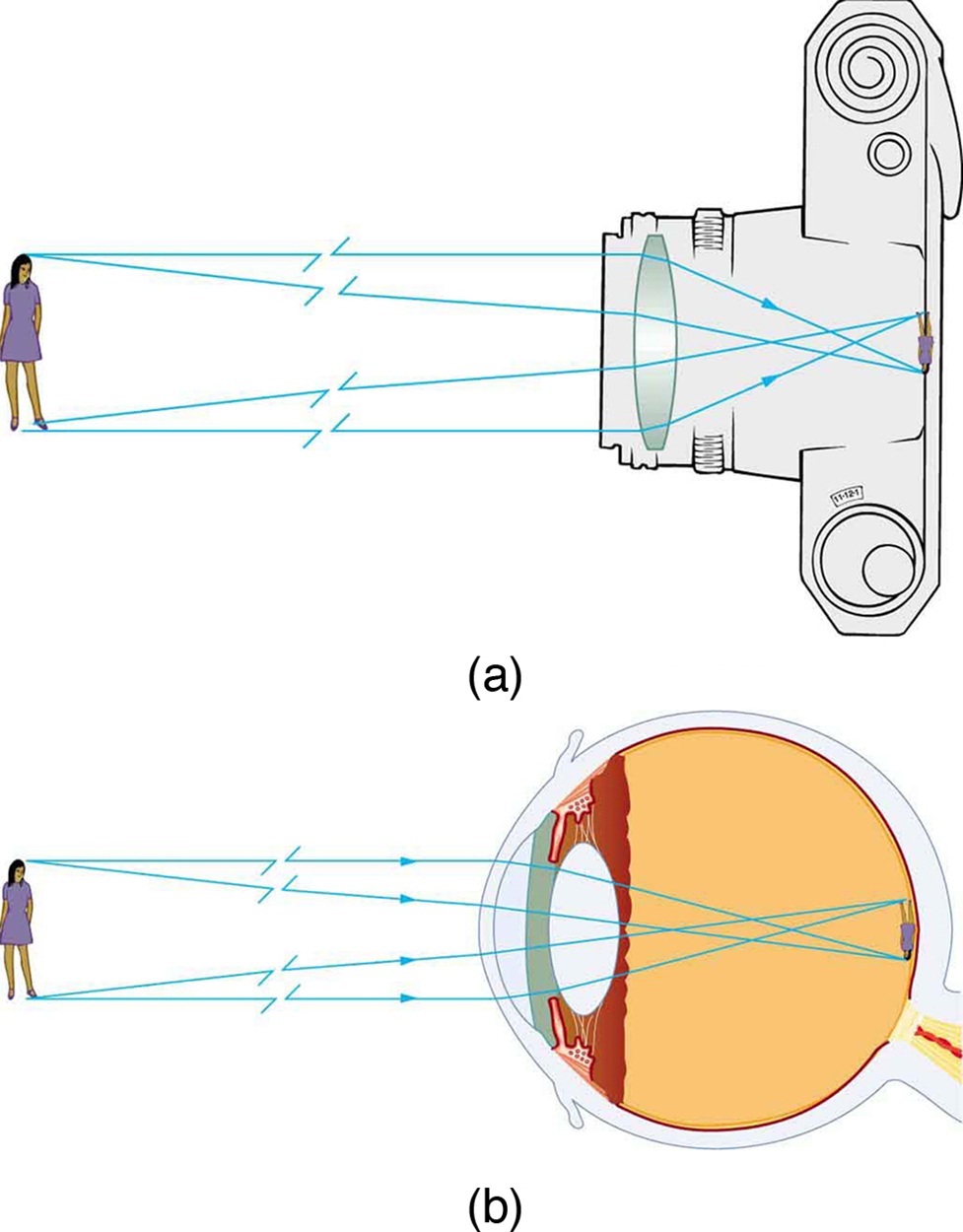
La imagen formada en Figura\(\PageIndex{7}\) es una imagen real, lo que significa que se puede proyectar. Es decir, los rayos de luz de un punto del objeto en realidad se cruzan en la ubicación de la imagen y pueden proyectarse sobre una pantalla, un trozo de película o la retina de un ojo, por ejemplo. La figura\(\PageIndex{8}\) muestra cómo una imagen de este tipo sería proyectada sobre película por una lente de cámara. Esta figura también muestra cómo una imagen real es proyectada sobre la retina por el cristalino de un ojo. Tenga en cuenta que la imagen está ahí tanto si se proyecta sobre una pantalla como si no.

Definición: IMAGEN REAL

La imagen en la que los rayos de luz de un punto en el objeto realmente se cruzan en la ubicación de la imagen y pueden proyectarse sobre una pantalla, un trozo de película o la retina de un ojo se llama imagen real.

Figura\(\PageIndex{8}\): Se pueden proyectar imágenes reales. (a) Una imagen real de la persona se proyecta en película. (b) La naturaleza convergente de las múltiples superficies que componen el ojo dan como resultado la proyección de una imagen real sobre la retina.

Varias distancias importantes aparecen en la Figura\(\PageIndex{7}\). Definimos\(d_{\mathrm{o}}\) que es la distancia del objeto, la distancia de un objeto desde el centro de una lente. La distancia de imagen\(d_{\mathrm{i}}\) se define como la distancia de la imagen desde el centro de una lente. A la altura del objeto y la altura de la imagen se les dan los símbolos\(h_{\mathrm{o}}\) y\(h_{\mathrm{i}}\), respectivamente. Las imágenes que aparecen verticales con relación al objeto tienen alturas que son positivas y las que están invertidas tienen alturas negativas. Usando las reglas del trazado de rayos y haciendo un dibujo a escala con papel y lápiz, así en Figura\(\PageIndex{8}\), podemos describir con precisión la ubicación y el tamaño de una imagen. Pero el beneficio real del trazado de rayos está en visualizar cómo se forman las imágenes en una variedad de situaciones. Para obtener información numérica, utilizamos un par de ecuaciones que se pueden derivar de un análisis geométrico de trazado de rayos para lentes delgadas. Las ecuaciones de lentes delgadas son

\[\frac{1}{d_{\mathrm{o}}}+\frac{1}{d_{\mathrm{i}}}=\frac{1}{f} \nonumber \]

y

\[\frac{h_{\mathrm{i}}}{h_{\mathrm{o}}}=-\frac{d_{\mathrm{i}}}{d_{\mathrm{o}}}=m. \nonumber \]

Definimos la relación entre la altura de la imagen y la altura del objeto (\(h_{\mathrm{i}} / h_{\mathrm{o}}\)) para que sea la ampliación\(m\). (El signo menos en la ecuación anterior se discutirá en breve.) Las ecuaciones de lentes delgadas son ampliamente aplicables a todas las situaciones que involucran lentes delgadas (y espejos “delgados”, como veremos más adelante). Exploraremos muchas características de la formación de imágenes en los siguientes ejemplos trabajados.

Definición: DISTANCIA DE LA

La distancia de la imagen desde el centro de la lente se llama distancia de imagen.

Ecuaciones de lente fina y aumento

\[\frac{1}{d_{\mathrm{o}}}+\frac{1}{d_{\mathrm{i}}}=\frac{1}{f} \nonumber\]

\[\frac{h_{\mathrm{i}}}{h_{\mathrm{o}}}=-\frac{d_{\mathrm{i}}}{d_{\mathrm{o}}}=m \nonumber\]

Ejemplo\(\PageIndex{2}\): Finding the Image of a Light Bulb Filament by Ray Tracing and by the Thin Lens Equations

Se coloca una bombilla de vidrio transparente a 0.750 m de una lente convexa que tiene una distancia focal de 0.500 m, como se muestra en la Figura\(\PageIndex{9}\). Utilice el trazado de rayos para obtener una ubicación aproximada de la imagen. Luego usa las ecuaciones de lente delgada para calcular (a) la ubicación de la imagen y (b) su aumento. Verifique que el trazado de rayos y las ecuaciones de lentes delgadas produzcan resultados consistentes.

Figura\(\PageIndex{9}\): Una bombilla colocada a 0.750 m de una lente que tiene una distancia focal de 0.500 m produce una imagen real en un tablero de póster como se discutió en el ejemplo anterior. El trazado de rayos predice la ubicación y el tamaño de la imagen.

Estrategia y Concepto

Dado que el objeto se coloca más lejos de una lente convergente que la distancia focal de la lente, esta situación es análoga a las ilustradas en la Figura\(\PageIndex{7}\) y la Figura\(\PageIndex{8}\). El trazado de rayos a escala debería producir resultados similares para di. Soluciones numéricas para\(d_{\mathrm{i}}\) y se\(m\) pueden obtener usando las ecuaciones de lente delgada, señalando que\(d_{\mathrm{o}}=0.750 \mathrm{~m} \text { and } f=0.500 \mathrm{~m}\).

Soluciones (Ray tracing)

El trazado de rayos a escala en la Figura\(\PageIndex{9}\) muestra dos rayos de un punto en el filamento de la bombilla cruzando alrededor de 1.50 m en el lado lejano de la lente. Así, la distancia de la imagen\(d_{\mathrm{i}}\) es de aproximadamente 1.50 m. De igual manera, la altura de la imagen basada en el trazado de rayos es mayor que la altura del objeto en aproximadamente un factor de 2, y la imagen se invierte. Así\(m\) es aproximadamente —2. El signo menos indica que la imagen está invertida.

Las ecuaciones de lente fina se pueden utilizar para encontrar a\(d_{\mathrm{i}}\) partir de la información dada:

\[\frac{1}{d_{\mathrm{o}}}+\frac{1}{d_{\mathrm{i}}}=\frac{1}{f}. \nonumber\]

Reorganizar para aislar\(d_{\mathrm{i}}\) da

\[\frac{1}{d_{\mathrm{i}}}=\frac{1}{f}-\frac{1}{d_{\mathrm{o}}}. \nonumber\]

Introducir cantidades conocidas da un valor para\(1 / d_{\mathrm{i}}\):

\[\frac{1}{d_{\mathrm{i}}}=\frac{1}{0.500 \mathrm{~m}}-\frac{1}{0.750 \mathrm{~m}}=\frac{0.667}{\mathrm{~m}}. \nonumber\]

Esto debe invertirse para encontrar\(d_{\mathrm{i}}\):

\[d_{\mathrm{i}}=\frac{\mathrm{m}}{0.667}=1.50 \mathrm{~m}. \nonumber\]

Tenga en cuenta que otra forma de encontrar\(d_{\mathrm{i}}\) es reorganizar la ecuación:

\[\frac{1}{d_{\mathrm{i}}}=\frac{1}{f}-\frac{1}{d_{\mathrm{o}}}. \nonumber\]

Esto produce la ecuación para la distancia de la imagen como:

\[d_{\mathrm{i}}=\frac{f d_{\mathrm{o}}}{d_{\mathrm{o}}-f}. \nonumber\]

Tenga en cuenta que aquí no hay inversión.

Las ecuaciones de lente fina se pueden utilizar para encontrar la ampliación\(m\), ya que ambas\(d_{\mathrm{i}}\) y\(d_{\mathrm{o}}\) son conocidas. Ingresando sus valores da

\[m=-\frac{d_{\mathrm{i}}}{d_{\mathrm{o}}}=-\frac{1.50 \mathrm{~m}}{0.750 \mathrm{~m}}=-2.00. \nonumber\]

Discusión

Tenga en cuenta que el signo menos hace que el aumento sea negativo cuando se invierte la imagen. El trazado de rayos y el uso de las ecuaciones de lentes delgadas producen resultados consistentes. Las ecuaciones de lente delgada dan los resultados más precisos, estando limitadas solo por la precisión de la información dada. El trazado de rayos está limitado por la precisión con la que se puede dibujar, pero es muy útil tanto conceptual como visualmente.

Las imágenes reales, como la considerada en el ejemplo anterior, están formadas por lentes convergentes siempre que un objeto esté más alejado de la lente que su distancia focal. Esto es cierto para los proyectores de películas, las cámaras y el ojo. Nos referiremos a éstas como imágenes del caso 1. Se forma una imagen del caso 1 cuando\(d_{0}>f\) y\(f\) es positiva, como en la Figura\(\PageIndex{10}\) (a). (Al final de esta sección aparece un resumen de los tres casos o tipos de formación de imágenes).

Se forma un tipo diferente de imagen cuando un objeto, como la cara de una persona, se sujeta cerca de una lente convexa. La imagen es vertical y más grande que el objeto, como se ve en la Figura\(\PageIndex{10}\) (b), por lo que la lente se llama lupa. Si lentamente sacas la lupa de la cara, verás que la ampliación aumenta de manera constante hasta que la imagen comienza a difuminarse. Al jalar la lupa aún más lejos se produce una imagen invertida como se ve en la Figura\(\PageIndex{10}\) (a). La distancia a la que la imagen se difumina, y más allá de la cual se invierte, es la distancia focal de la lente. Para utilizar una lente convexa como lupa, el objeto debe estar más cerca de la lente convergente que su distancia focal. A esto se le llama una imagen del caso 2. Se forma una imagen del caso 2 cuando\(d_{\mathrm{o}}<f\) y\(f\) es positiva.

Figura\(\PageIndex{10}\): (a) Cuando una lente convergente se mantiene más alejada de la cara que la distancia focal de la lente, se forma una imagen invertida. Esta es una imagen de caso 1. Tenga en cuenta que la imagen está enfocada pero la cara no, porque la imagen está mucho más cerca de la cámara que toma esta fotografía que de la cara. (crédito: DamongMan, Flickr) (b) Se produce una imagen ampliada de un rostro colocándolo más cerca de la lente convergente que de su distancia focal. Esta es una imagen del caso 2. (crédito: Casey Fleser, Flickr)

La figura\(\PageIndex{11}\) utiliza el trazado de rayos para mostrar cómo se forma una imagen cuando un objeto se mantiene más cerca de una lente convergente que su distancia focal. Los rayos que provienen de un punto común en el objeto continúan divergiendo después de pasar por la lente, pero todos parecen originarse a partir de un punto en la ubicación de la imagen. La imagen está en el mismo lado de la lente que el objeto y está más lejos de la lente que el objeto. Esta imagen, como todas las imágenes del caso 2, no se puede proyectar y, de ahí, se llama imagen virtual. Los rayos de luz sólo parecen originarse en una imagen virtual; en realidad no pasan por esa ubicación en el espacio. Una pantalla colocada en la ubicación de una imagen virtual recibirá solo luz difusa del objeto, no rayos enfocados de la lente. Adicionalmente, una pantalla colocada en el lado opuesto de la lente recibirá rayos que aún divergen, por lo que no se proyectará ninguna imagen sobre ella. Podemos ver la imagen ampliada con nuestros ojos, porque la lente del ojo converge los rayos en una imagen real proyectada sobre nuestra retina. Por último, observamos que una imagen virtual es vertical y más grande que el objeto, es decir, que la ampliación es positiva y mayor que 1.

Figura\(\PageIndex{11}\): El trazado de rayos predice la ubicación y el tamaño de la imagen para un objeto mantenido más cerca de una lente convergente que su distancia focal. El rayo 1 entra paralelo al eje y sale por el punto focal en el lado opuesto, mientras que el rayo 2 pasa por el centro de la lente sin cambiar de trayectoria. Los dos rayos continúan divergiendo al otro lado de la lente, pero ambos parecen provenir de un punto común, ubicando la imagen vertical, magnificada, virtual. Esta es una imagen del caso 2.

Definición: Imagen virtual

Una imagen que está en el mismo lado de la lente que el objeto y que no se puede proyectar en una pantalla se llama imagen virtual.

Ejemplo\(\PageIndex{3}\): Image Produced by a Magnifying Glass

Supongamos que la página del libro en la Figura\(\PageIndex{11}\) (a) se sostiene a 7.50 cm de una lente convexa de distancia focal de 10.0 cm, tal como podría tener una lupa típica. ¿Qué ampliación se produce?

Estrategia y Concepto

Se nos da eso\(d_{\mathrm{o}}=7.50 \mathrm{~cm}\) y\(f=10.0 \mathrm{~cm}\), así tenemos una situación en la que el objeto se coloca más cerca de la lente que su distancia focal. Por lo tanto, esperamos obtener una imagen virtual de caso 2 con un aumento positivo que sea mayor que 1. El trazado de rayos produce una imagen como la que se muestra en la Figura\(\PageIndex{11}\), pero usaremos las ecuaciones de lente delgada para obtener soluciones numéricas en este ejemplo.

Solución

Para encontrar la ampliación m, tratamos de utilizar la ecuación de ampliación,\(m=-d_{\mathrm{i}} / d_{\mathrm{o}}\). No tenemos un valor para\(d_{\mathrm{i}}\), por lo que primero debemos encontrar la ubicación de la imagen usando la ecuación de lente. (El procedimiento es el mismo que se siguió en el ejemplo anterior, donde\(d_{\mathrm{o}}\) y\(f\) se conocían.) Reorganizar la ecuación de aumento para aislar\(d_{\mathrm{i}}\) da

\[\frac{1}{d_{\mathrm{i}}}=\frac{1}{f}-\frac{1}{d_{\mathrm{o}}}. \nonumber\]

Ingresando valores conocidos, obtenemos un valor para\(1 / d_{\mathrm{i}}\):

\[\frac{1}{d_{\mathrm{i}}}=\frac{1}{10.0 \mathrm{~cm}}-\frac{1}{7.50 \mathrm{~cm}}=\frac{-0.0333}{\mathrm{~cm}}. \nonumber\]

Esto debe invertirse para encontrar\(d_{\mathrm{i}}\):

\[d_{\mathrm{i}}=-\frac{\mathrm{cm}}{0.0333}=-30.0 \mathrm{~cm}. \nonumber\]

Ahora la ecuación de lente delgada se puede utilizar para encontrar el aumento\(m\), ya que ambos\(d_{\mathrm{i}}\) y\(d_{\mathrm{o}}\) son conocidos. Ingresando sus valores da

\[m=-\frac{d_{\mathrm{i}}}{d_{\mathrm{o}}}=-\frac{-30.0 \mathrm{~cm}}{7.5 \mathrm{~cm}}=4.00. \nonumber\]

Discusión

Una serie de resultados en este ejemplo son ciertos para todas las imágenes del caso 2, además de ser consistentes con la Figura\(\PageIndex{11}\). El aumento es realmente positivo (como se predijo), lo que significa que la imagen es vertical. El aumento también es mayor que 1, lo que significa que la imagen es más grande que el objeto, en este caso, en un factor de 3. Tenga en cuenta que la distancia de la imagen es negativa. Esto significa que la imagen está en el mismo lado de la lente que el objeto. Así la imagen no se puede proyectar y es virtual. (Los valores negativos de\(d_{\mathrm{i}}\) ocurren para imágenes virtuales.) La imagen está más lejos de la lente que del objeto, ya que la distancia de la imagen es mayor en magnitud que la distancia del objeto. La ubicación de la imagen no es obvia cuando miras a través de una lupa. De hecho, dado que la imagen es más grande que el objeto, se puede pensar que la imagen está más cerca que el objeto. Pero la imagen está más lejos, hecho que es útil para corregir la hipermetropía, como veremos en una sección posterior.

Un tercer tipo de imagen está formado por una lente divergente o cóncava. Intenta mirar a través de anteojos destinados a corregir la miopía. (Ver Figura\(\PageIndex{12}\).) Verás una imagen que es vertical pero más pequeña que el objeto. Esto quiere decir que la ampliación es positiva pero menor a 1. El diagrama de rayos en la Figura\(\PageIndex{13}\) muestra que la imagen está en el mismo lado de la lente que el objeto y, por lo tanto, no se puede proyectar, es una imagen virtual. Tenga en cuenta que la imagen está más cerca de la lente que del objeto. Se trata de una imagen de caso 3, formada para cualquier objeto por una distancia focal negativa o lente divergente.

Figura\(\PageIndex{12}\): Un automóvil visto a través de una lente cóncava o divergente se ve en posición vertical. Esta es una imagen del caso 3. (crédito: Daniel Oines, Flickr)

Figura\(\PageIndex{13}\): El trazado de rayos predice la ubicación y el tamaño de la imagen para una lente cóncava o divergente. El rayo 1 entra paralelo al eje y se dobla de manera que parece originarse desde el punto focal. El rayo 2 pasa por el centro de la lente sin cambiar la trayectoria. Los dos rayos parecen provenir de un punto común, ubicando la imagen vertical. Se trata de una imagen de caso 3, que está más cerca de la lente que el objeto y menor en altura.

Ejemplo\(\PageIndex{4}\): Image Produced by a Concave Lens

Supongamos que un objeto como una página de libro se sostiene a 7.50 cm de una lente cóncava de distancia focal —10.0 cm. Tal lente podría usarse en anteojos para corregir miopía pronunciada. ¿Qué ampliación se produce?

Estrategia y Concepto

Este ejemplo es idéntico al anterior, excepto que la distancia focal es negativa para una lente cóncava o divergente. El método de solución es así el mismo, pero los resultados son diferentes en formas importantes.

Solución

Para encontrar la ampliación\(m\), primero debemos encontrar la distancia de la imagen\(d_{\mathrm{i}}\) usando la ecuación de lente delgada

\[\frac{1}{d_{\mathrm{i}}}=\frac{1}{f}-\frac{1}{d_{\mathrm{o}}}, \nonumber\]

o su reordenamiento alternativo

\[d_{i}=\frac{f d_{\mathrm{o}}}{d_{\mathrm{o}}-f}. \nonumber\]

Se nos da eso\(f=-10.0 \mathrm{~cm}\) y\(d_{\mathrm{o}}=7.50 \mathrm{~cm}\). Al ingresar estos se obtiene un valor para\(1 / d_{\mathrm{i}}\):

\[\frac{1}{d_{\mathrm{i}}}=\frac{1}{-10.0 \mathrm{~cm}}-\frac{1}{7.50 \mathrm{~cm}}=\frac{-0.2333}{\mathrm{~cm}}. \nonumber\]

Esto debe invertirse para encontrar\(d_{\mathrm{i}}\):

\[d_{\mathrm{i}}=-\frac{\mathrm{cm}}{0.2333}=-4.29 \mathrm{~cm}. \nonumber\]

O

\[d_{\mathrm{i}}=\frac{(7.5)(-10)}{(7.5-(-10))}=-75 / 17.5=-4.29 \mathrm{~cm}. \nonumber\]

Ahora la ecuación de ampliación se puede utilizar para encontrar la ampliación\(m\), ya que ambos\(d_{\mathrm{i}}\) y\(d_{\mathrm{o}}\) son conocidos. Ingresando sus valores da

\[m=-\frac{d_{\mathrm{i}}}{d_{\mathrm{o}}}=-\frac{-4.29 \mathrm{~cm}}{7.50 \mathrm{~cm}}=0.571. \nonumber\]

Discusión

Una serie de resultados en este ejemplo son ciertos para todas las imágenes del caso 3, además de ser consistentes con la Figura\(\PageIndex{13}\). El aumento es positivo (como se predijo), lo que significa que la imagen es vertical. El aumento también es menor que 1, lo que significa que la imagen es más pequeña que el objeto, en este caso, un poco más de la mitad de su tamaño. La distancia de la imagen es negativa, lo que significa que la imagen está en el mismo lado de la lente que el objeto. (La imagen es virtual.) La imagen está más cerca de la lente que del objeto, ya que la distancia de la imagen es menor en magnitud que la distancia del objeto. La ubicación de la imagen no es obvia cuando miras a través de una lente cóncava. De hecho, dado que la imagen es más pequeña que el objeto, se puede pensar que está más lejos. Pero la imagen está más cerca que el objeto, hecho que es útil para corregir la miopía, como veremos en una sección posterior.

En la tabla\(\PageIndex{1}\) se resumen los tres tipos de imágenes formadas por lentes simples delgadas. Estas son referidas como imágenes de los casos 1, 2 y 3. Las lentes convexas (convergentes) pueden formar imágenes reales o virtuales (casos 1 y 2, respectivamente), mientras que las lentes cóncavas (divergentes) pueden formar solo imágenes virtuales (siempre caso 3). Las imágenes reales siempre están invertidas, pero pueden ser más grandes o más pequeñas que el objeto. Por ejemplo, un proyector de diapositivas forma una imagen más grande que la diapositiva, mientras que una cámara hace que una imagen sea más pequeña que el objeto que se está fotografiando. Las imágenes virtuales siempre están en posición vertical y no se pueden proyectar. Las imágenes virtuales son más grandes que el objeto solo en el caso 2, donde se usa una lente convexa. La imagen virtual producida por una lente cóncava es siempre más pequeña que el objeto, una imagen de caso 3. Podemos ver y fotografiar imágenes virtuales solo mediante el uso de una lente adicional para formar una imagen real.

Tabla\(\PageIndex{1}\): Tres tipos de imágenes formadas por lentes delgadas

Tipo	Formado cuando	Tipo de imagen	d i	m
Caso 1	\(f\)positivo,\(d_{o}>f\)	real	positivo	negativo
Caso 2	\(f\)positivo,\(d_{o}<f\)	virtual	negativo	positivo,\(m>1\)
Caso 3	\(f\)negativo	virtual	negativo	positivo,\(m<1\)

Experimento para llevar a casa: concentrar la luz solar

Encuentra varias lentes y determina si son convergentes o divergentes. En general los que son más gruesos cerca de los bordes son divergentes y los que son más gruesos cerca del centro están convergiendo. En un día soleado, tome las lentes convergentes afuera e intente enfocar la luz solar en un trozo de papel. Determinar las distancias focales de las lentes. Ten cuidado porque el papel puede comenzar a quemarse, dependiendo del tipo de lente que hayas seleccionado.

Resumen de la Sección

• Los rayos de luz que entran en una lente convergente paralela a su eje se cruzan entre sí en un solo punto en el lado opuesto.
• Para una lente convergente, el punto focal es el punto en el que se cruzan los rayos de luz convergentes; para una lente divergente, el punto focal es el punto a partir del cual los rayos de luz divergentes parecen originarse.
• La distancia desde el centro de la lente hasta su punto focal se llama distancia focal\(f\).
• La potencia\(P\) de una lente se define como la inversa de su distancia focal,\(P=\frac{1}{f}\).
• Una lente que hace que los rayos de luz se doblen alejándose de su eje se denomina lente divergente.
• El trazado de rayos es la técnica de determinar gráficamente los caminos que toman los rayos de luz.
• La imagen en la que los rayos de luz de un punto en el objeto realmente se cruzan en la ubicación de la imagen y pueden proyectarse sobre una pantalla, un trozo de película o la retina de un ojo se llama imagen real.
• Las ecuaciones de lentes delgadas son\(\frac{1}{d_{\mathrm{o}}}+\frac{1}{d_{\mathrm{i}}}=\frac{1}{f}\) y\(\frac{h_{\mathrm{i}}}{h_{\mathrm{o}}}=-\frac{d_{\mathrm{i}}}{d_{\mathrm{o}}}=m\) (aumento).
• La distancia de la imagen desde el centro de la lente se llama distancia de imagen.
• Una imagen que está en el mismo lado de la lente que el objeto y que no se puede proyectar en una pantalla se llama imagen virtual.

Glosario

lente convergente

una lente convexa en la que los rayos de luz que entran paralelos a su eje convergen en un solo punto en el lado opuesto

lente divergente

una lente cóncava en la que los rayos de luz que entran en él paralelos a su eje se doblan (divergen) de su eje

punto focal

para una lente o espejo convergente, el punto en el que se cruzan los rayos de luz convergentes; para una lente o espejo divergente, el punto a partir del cual los rayos de luz divergentes parecen originarse

distancia focal

distancia desde el centro de una lente o espejo curvo hasta su punto focal

aumento

relación de altura de imagen a altura de objeto

poder

inverso de la distancia focal

imagen real

imagen que se puede proyectar

imagen virtual

imagen que no se puede proyectar