12.7: Teoría de Bohr del átomo de hidrógeno

Objetivos de aprendizaje

• Describir modelos atómicos tempranos.
• Explicar la teoría de Bohr sobre el átomo de hidrógeno.
• Distinguir entre características correctas e incorrectas del modelo Bohr, a la luz de la mecánica cuántica moderna.

El gran físico danés Niels Bohr (1885—1962) hizo uso inmediato del modelo planetario del átomo de Rutherford. (Figura\(\PageIndex{1}\)). Bohr se convenció de su validez y pasó parte de 1912 en el laboratorio de Rutherford. En 1913, tras regresar a Copenhague, comenzó a publicar su teoría del átomo más simple, el hidrógeno, basada en el modelo planetario del átomo. Durante décadas, se habían hecho muchas preguntas sobre las características atómicas. Desde sus tamaños hasta sus espectros, se sabía mucho sobre los átomos, pero poco se había explicado en términos de las leyes de la física. La teoría de Bohr explicó el espectro atómico del hidrógeno y estableció principios nuevos y ampliamente aplicables en la mecánica cuántica.

Figura\(\PageIndex{1}\): Niels Bohr, físico danés, utilizó el modelo planetario del átomo para explicar el espectro atómico y el tamaño del átomo de hidrógeno. Sus múltiples contribuciones al desarrollo de la física atómica y la mecánica cuántica, su influencia personal en muchos estudiantes y colegas, y su integridad personal, especialmente ante la opresión nazi, le valieron un lugar destacado en la historia. (crédito: Autor desconocido, vía Wikimedia Commons)

Espectros atómicos

Desde hace más de un siglo se sabe que los espectros de emisión y absorción atómicos y moleculares son discretos (o cuantificados). Mucho antes de que se entendieran desde los primeros principios, los químicos han estado utilizando los espectros de emisión y absorción para la identificación de elementos. La figura\(\PageIndex{2}\) muestra el espectro de emisión de hierro, por ejemplo. Ningún otro elemento emite exactamente el mismo conjunto de frecuencias de luz. Con el descubrimiento de la subestructura del átomo y el descubrimiento del fotón (o más precisamente, la comprensión refinada de la naturaleza de partículas de las ondas electromagnéticas donde la energía de las partículas es proporcional a la frecuencia de las ondas electromagnéticas), estas frecuencias resonantes de luz emitida por los átomos podrían ser utilizado para inferir un modelo atómico.

Figura\(\PageIndex{2}\): La parte (a) muestra, de izquierda a derecha, un tubo de descarga, una hendidura y una rejilla de difracción que producen un espectro lineal. La parte (b) muestra el espectro de líneas de emisión para hierro. Las líneas discretas implican estados energéticos cuantificados para los átomos que las producen. El espectro de líneas para cada elemento es único, proporcionando una herramienta analítica poderosa y muy utilizada, y muchos espectros de línea fueron bien conocidos durante muchos años antes de que pudieran explicarse con la física. (crédito para (b): Yttrium91, Wikimedia Commons)

Para el átomo de hidrógeno, el elemento más ligero con el átomo más simple, un patrón para su espectro lineal fue notado por los experimentalistas (ver Figura\(\PageIndex{3}\)). Todas las longitudes de onda del espectro lineal podrían describirse mediante una fórmula siguiente, para la elección adecuada de dos números enteros\(n_{i}\) y\(n_{f}\):

\[\frac{1}{\lambda}=R\left(\frac{1}{n_{\mathrm{f}}^{2}}-\frac{1}{n_{\mathrm{i}}^{2}}\right), \label{1}\]

donde\(\lambda\) es la longitud de onda de la radiación EM emitida y\(R\) es la constante de Rydberg, determinada por el experimento para ser

\[R=1.097 \times 10^{7} / \mathrm{m}\left(\text { or } \mathrm{m}^{-1}\right). \nonumber \]

El\(n_{\mathrm{f}}\) es un entero positivo asociado a una serie específica, que llevan el nombre de sus descubridores. Para la serie Lyman,\(n_{\mathrm{f}}=1\); para la serie Balmer,\(n_{\mathrm{f}}=2\); para la serie Paschen,\(n_{\mathrm{f}}=3\); y así sucesivamente. La serie Lyman está completamente en la UV, mientras que parte de la serie Balmer es visible con el resto UV. La serie Paschen y todo lo demás son enteramente IR. Aparentemente hay un número ilimitado de series, aunque se encuentran progresivamente más lejos en el infrarrojo y se vuelven difíciles de observar a medida que\(\n_{\mathrm{f}}\) aumenta. El\(n_{\mathrm{i}}\) es un entero positivo mayor que\(n_{\mathrm{f}}\). Entonces por ejemplo, para la serie Balmer,\(n_{\mathrm{f}}=2\) y\(n_{\mathrm{i}}=3,4,5,6, \ldots\).

Entonces, antes del modelo de Bohr del átomo de hidrógeno, tal era la imagen de la teoría atómica, llena de datos sugerentes (e incluso bien organizados) y sin explicación unificadora. Se cita a Ernest Rutherford diciendo: “Toda la ciencia es física o coleccionismo de estampillas”. Lo que quiso decir es que hay ramas de la ciencia cuyos practicantes estarían satisfechos con una colección de datos interesantes (es decir, “recolección de sellos”). Pero lo que hace a la física física es la búsqueda del marco teórico aportando explicaciones basadas en principios fundamentales, no en descripciones idiosincrásicas. El modelo de Bohr llevó la ciencia de la espectroscopia a la física.

Figura\(\PageIndex{3}\): Un esquema del espectro de hidrógeno muestra varias series nombradas por aquellos que más contribuyeron a su determinación. Parte de la serie Balmer está en el espectro visible, mientras que la serie Lyman está completamente en la UV, y la serie Paschen y otras están en el IR. Los valores de\(n_{\mathrm{f}}\) y\(n_{\mathrm{i}}\) se muestran para algunas de las líneas.

Modelo de Bohr para Hidrógeno

El modelo planetario del átomo sugerido por Rutherford estaba en problemas. Si bien el modelo proporcionó una posible imagen de cómo el núcleo atómico muy pequeño podría estar dispuesto con los electrones en una disposición estable, no proporcionó el tamaño de las órbitas de electrones (lo que estaría relacionado con el tamaño del átomo), y la disposición no era realmente estable, un electrón en órbita es un carga oscilante; una carga oscilante emite ondas electromagnéticas; las ondas electromagnéticas llevan energía; así como el electrón pierde energía, caería en el protón. Según algunas estimaciones, ¡esto ocurriría en tan poco tiempo como\(10^{-7} \mathrm{~s}\)!

El punto de partida de Bohr para su exitoso modelo fue este: propuso que se cuantificaran las órbitas de electrones en átomos. Para entender completamente esta afirmación, podemos comparar las órbitas de electrones en átomos con las órbitas de planetas en el sistema solar. Las órbitas de los planetas no están cuantificadas. Si bien las leyes de la física gobiernan cómo se mueven los planetas en el sistema solar (ver por ejemplo, las leyes de Kepler, o su derivación por Newton comenzando con la ley del cuadrado inverso de la gravitación), no existe ninguna ley de la física que dicte qué tan lejos debe estar cada cuerpo en el sistema solar del Sol. Entonces no se cuantifican las órbitas de los planetas.

Entonces, lo que Bohr estaba proponiendo era una ley de la física completamente nueva que nadie había conocido antes. En un sentido, no era completamente nuevo (Planck y Einstein ya disfrutaron de algunos éxitos al sugerir la cuantificación de la energía en osciladores térmicos y radiación EM); en otro sentido, fue una gran ruptura con siglos de mecánica clásica. Esta fue la regla de cuantificación de Bohr: se cuantifica el momento angular de un electrón en su órbita. En forma matemática,

\[L=n \hbar, \nonumber \]

donde nn podría tomar cualquier valor entero positivo (\(n=1,2,3, \ldots\)), y\(\hbar\) se conoce como la constante de Planck reducida (\(\hbar=h / 2 \pi\)). Y el momento angular\(L\), como recordarás del capítulo anterior, viene dado por lo siguiente para una partícula en una órbita circular uniforme:\(L=m v r\), donde\(m\) está la masa de la partícula,\(v\) es la velocidad de la partícula en órbita, y rr es el radio de órbita circular. Usando esto como punto de partida, el análisis semiclásico del movimiento orbital produce un conjunto completo de valores cuantificados (es decir permitidos) de distancia orbital\(\left(r_{n}\right)\)\(\left(v_{n}\right)\), velocidad orbital y energía orbital\(\left(E_{n}\right)\), entre otros (ver: Tabla\(\PageIndex{1}\) para un resumen).

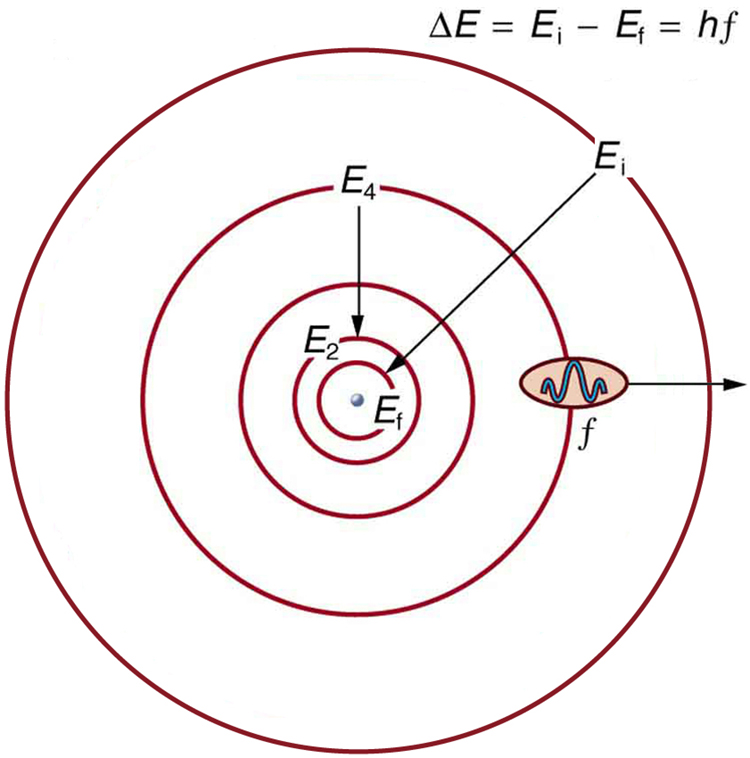
Con las energías orbitales cuantificadas para el electrón, tenemos una explicación lista para las características de los espectros atómicos. La radiación EM se emite cuando un electrón pasa de un nivel de energía superior (\(E_{i}\)) a un nivel de energía más bajo (\(E_{f}\)), con el fotón arrastrando la diferencia de energía,

\[h f=\Delta E=E_{i}-E_{f}, \label{2} \]

donde\(f\) está la frecuencia del fotón. La figura\(\PageIndex{4}\) muestra una representación esquemática de esta relación. Con solo valores discretos de energía\(E_{n}\) permitidos, solo se permiten valores discretos de frecuencia (\(f\)) y longitud de onda (\(\lambda\)) también, como se muestra en los espectros de línea.

Figura\(\PageIndex{4}\): El modelo planetario del átomo, modificado por Bohr, tiene cuantificadas las órbitas de los electrones. Solo se permiten ciertas órbitas, explicando por qué los espectros atómicos son discretos (cuantificados). La energía arrastrada de un átomo por un fotón proviene de la caída de electrones de una órbita permitida a otra y así se cuantifica. Esto también es cierto para la absorción atómica de fotones.

Figura\(\PageIndex{5}\): Un diagrama de nivel de energía traza la energía verticalmente y es útil para visualizar los estados energéticos de un sistema y las transiciones entre ellos. Este diagrama es para los electrones de átomos de hidrógeno, mostrando una transición entre dos órbitas que tienen energías\(E_{4}\) y\(E_{2}\).

El diagrama de nivel de energía, mostrado en la Figura\(\PageIndex{5}\), es otra manera conveniente de ilustrar estas relaciones. Los niveles de energía permitidos para el átomo se trazan verticalmente con el estado más bajo (o estado fundamental) en la parte inferior y con estados excitados por encima de ese. Las energías de las líneas en un espectro atómico corresponden a las diferencias en los niveles de energía en el diagrama de niveles (la figura ilustra una transición de\(E_{4}\) a\(E_{2}\), que se mostraría en el espectro atómico como una línea).

Cuadro\(\PageIndex{1}\): Resumen de cantidades cuantificadas en el modelo Bohr del átomo de hidrógeno. Las derivaciones completas toman algo de álgebra, y utilizan: (1) fuerza centrípeta debida a la fuerza de Coulomb, (2) relación entre el radio orbital cuantificado y la velocidad orbital cuantificada a través de la cuantificación del momento angular, y (3) expresión para la energía total, incluyendo la energía cinética orbital y la Energía potencial de Coulomb.

Cantidad cuantificada	Dependencia del número cuántico\(n\)	Expresión completa
momento angular:\(L_{n}\)	\ (n\) ">proporcional a\(n\)	\(L_{n}=n \hbar\)
radio orbital:\(r_{n}\)	\ (n\) ">proporcional a\(n^{2}\)	\(r_{n}=\frac{n^{2} \hbar^{2}}{m k e^{2}}\)
velocidad orbital:\(v_{n}\)	\ (n\) ">proporcional a\(\frac{1}{n}\)	\(v_{n}=\frac{k e^{2}}{n \hbar}\)
energía orbital:\(E_{n}\)	\ (n\) ">proporcional a\(\frac{1}{n^{2}}\)	\(E_{n}=-\frac{m k^{2} e^{4}}{2 n^{2} \hbar^{2}}=-\frac{13.6}{n^{2}} \mathrm{eV}\)

Dos resultados clave son dignos de destacar. El primero es el radio de Bohr, o el radio orbital más pequeño\(a\), dado para\(n=1\),

\ [\ begin {align*}
a &=r_ {1} =\ hbar^ {2}/m k e^ {2}\\
&=0.529\ veces 10^ {-10}\ mathrm {~m}.
\ end {alinear*}\]

Esta es la predicción del modelo de Bohr para el tamaño del átomo, hecha con nada más que constantes eléctricas, masa del electrón, y la constante de Planck, y esta predicción teórica coincide bastante bien con tamaños medidos experimentalmente de átomos.

El segundo es la derivación de la fórmula de Rydberg, dada primero en la Ecuación\(\eqref{1}\). Para derivar esto, comenzamos con Ecuación\(\eqref{2}\) y sustituimos en expresiones las energías de hidrógeno de la Tabla\(\PageIndex{1}\):

\ [\ begin {align*}
h f &=-\ frac {m k^ {2} e^ {4}} {2 n_ {i} ^ {2}\ hbar^ {2}} -\ izquierda (-\ frac {m k^ {2} e^ {4}} {2 n_ {f} ^ {2}\ hbar^ {2}}\ derecha)\
&\ =\ frac {m k^ {2} e^ {4}} {2\ hbar^ {2}}\ izquierda (\ frac {1} {n_ {f} ^ {2}} -\ frac {1} {n_ {i} ^ {2}}\ derecha)
\ end {align*}\]

La frecuencia\(f\) es igual a\(c / \lambda\). Tapando esto y resolviendo\(1 / \lambda\) mientras también reemplazamos todas las instancias de\(\hbar\) con\(h / 2 \pi\), obtenemos,

\[\frac{1}{\lambda}=\frac{2 \pi^{2} m k^{2} e^{4}}{h^{3} c}\left(\frac{1}{n_{f}}-\frac{1}{n_{i}}\right), \nonumber \]

que produce una expresión analítica para la constante de Rydberg,

\[R=\frac{2 \pi^{2} m k^{2} e^{4}}{h^{3} c}=1.097 \times 10^{7} \mathrm{~m}^{-1}. \nonumber \]

La figura\(\PageIndex{6}\) muestra un diagrama de nivel de energía para hidrógeno que también ilustra cómo las diversas series espectrales para hidrógeno se relacionan con las transiciones entre niveles de energía.

Figura\(\PageIndex{6}\): Diagrama de nivel de energía para hidrógeno que muestra las series de transiciones de Lyman, Balmer y Paschen. Las energías orbitales se calculan utilizando la ecuación anterior, derivada primero por Bohr.

Vemos que la teoría de Bohr del átomo de hidrógeno responde a la pregunta de por qué esta fórmula previamente conocida describe el espectro de hidrógeno. Es porque los niveles de energía son proporcionales a\(1 / n^{2}\), donde\(n\) es un entero no negativo. Una transición a la baja libera energía, por lo que\(n_{\mathrm{i}}\) debe ser mayor que\(n_{\mathrm{f}}\). Las diversas series son aquellas en las que las transiciones terminan en cierto nivel. Para la serie Lyman,\(n_{\mathrm{f}}=1\) —es decir, todas las transiciones terminan en el estado fundamental (ver también Figura\(\PageIndex{6}\)). Para la serie Balmer,\(n_{\mathrm{f}}=2\), o todas las transiciones terminan en el primer estado excitado; y así sucesivamente. Lo que alguna vez fue una receta ahora se basa en la física, y algo nuevo está emergiendo: el momento angular se cuantifica.

Triunfos y límites de la teoría de Bohr

Bohr hizo lo que nadie había podido hacer antes. No sólo explicó el espectro del hidrógeno, calculó correctamente el tamaño del átomo a partir de la física básica. Algunas de sus ideas son ampliamente aplicables. Las energías orbitales de electrones se cuantifican en todos los átomos y moléculas. Se cuantifica el momento angular. Los electrones no entran en espiral hacia el núcleo, como se esperaba clásicamente. Se trata de grandes triunfos.

Pero hay límites a la teoría de Bohr. No se puede aplicar a átomos multielectrones, ni siquiera uno tan simple como un átomo de helio de dos electrones. El modelo de Bohr es un modelo semiclásico. Las órbitas se cuantifican (mecánica cuántica) pero se supone que son caminos circulares simples (clásicos). A medida que se desarrolló la mecánica cuántica, quedó claro que no hay órbitas bien definidas; más bien, hay “nubes” de probabilidad. La teoría de Bohr tampoco explicó que algunas líneas espectrales son dobletes (divididas en dos) cuando se examinan de cerca. Estas deficiencias se abordan en modelos atómicos posteriores, totalmente cuántico-mecánicos, pero hay que tener en cuenta que Bohr no falló. Más bien, dio pasos muy importantes en el camino hacia un mayor conocimiento y sentó las bases.

Resumen de la Sección

• El modelo planetario del átomo representa electrones orbitando el núcleo en la forma en que los planetas orbitan el sol. Bohr utilizó el modelo planetario para desarrollar la primera teoría razonable del hidrógeno, el átomo más simple. Se cuantifican los espectros atómicos y moleculares, con longitudes de onda del espectro de hidrógeno dadas por la fórmula

  \[\frac{1}{\lambda}=R\left(\frac{1}{n_{\mathrm{f}}^{2}}-\frac{1}{n_{\mathrm{i}}^{2}}\right), \nonumber\]

  donde\(\lambda\) es la longitud de onda de la radiación EM emitida y\(R\) es la constante de Rydberg, que tiene el valor

  \[R=1.097 \times 10^{7} \mathrm{~m}^{-1}. \nonumber\]

• Las constantes\(n_{\mathrm{i}}\) y\(n_{\mathrm{f}}\) son enteros positivos, y\(n_{\mathrm{i}}\) deben ser mayores que\(n_{\mathrm{f}}\).
• Bohr propuso correctamente que se cuantificaran la energía y los radios de las órbitas de electrones en átomos, con energía para transiciones entre órbitas dada por

  \[\Delta E=h f=E_{\mathrm{i}}-E_{\mathrm{f}}, \nonumber\]

• donde\(\Delta E\) es el cambio de energía entre las órbitas inicial y final y\(hf\) es la energía de un fotón absorbido o emitido. Es útil graficar las energías orbitales en una gráfica vertical llamada diagrama de nivel de energía.

• Bohr propuso que las órbitas permitidas son circulares y deben haber cuantificado el momento angular orbital dado por

  \[L=m_{e} v r_{n}=n \frac{h}{2 \pi}(n=1,2,3 \ldots), \nonumber\]

  donde \(L\)está el momento angular,\(r_{n}\) es el radio de la \(n\mathrm{th}\)órbita, y \(h\)es la constante de Planck.
• Las cantidades orbitales cuantificadas adicionales (radio orbital, velocidad orbital y energía orbital) se pueden derivar a partir de la suposición de Bohr, y producen predicciones consistentes con la fórmula experimental de Rydberg.
• Si bien el modelo semiclásico del átomo de Bohr no da cuenta de todos los hechos experimentales sobre el átomo, es un importante escalón hacia modelos completamente cuántico-mecánicos del átomo.

Glosario

longitudes de onda del espectro de hidrógeno

las longitudes de onda de la luz visible del hidrógeno; puede calcularse por\(\frac{1}{\lambda}=R\left(\frac{1}{n_{\mathrm{f}}^{2}}-\frac{1}{n_{\mathrm{i}}^{2}}\right)\)

Constante de Rydberg

una constante física relacionada con los espectros atómicos con un valor establecido de\(1.097 \times 10^{7} \mathrm{~m}^{-1}\)

interferencia de doble rendija

un experimento en el que ondas o partículas de una sola fuente inciden sobre dos hendiduras para que se pueda observar el patrón de interferencia resultante

diagrama de nivel de energía

un diagrama utilizado para analizar el nivel de energía de los electrones en las órbitas de un átomo

Radio de Bohr

el radio medio de la órbita de un electrón alrededor del núcleo de un átomo de hidrógeno en su estado fundamental

átomo similar al hidrógeno

cualquier átomo con un solo electrón

energías de átomos similares a hidrógeno

Fórmula de Bohr para energías de estados electrónicos en átomos similares a hidrógeno:\(E_{n}=-\frac{Z^{2}}{n^{2}} E_{0}(n=1,2,3, \ldots)\)