8.2: Distorsión del espacio y el tiempo

7.2.1 La transformación de Lorentz

La relatividad dice que cuando dos observadores se encuentran en distintos marcos de referencia, cada observador considera distorsionada la percepción del tiempo del otro. También veremos que algo similar sucede con sus observaciones de distancias, por lo que tanto el espacio como el tiempo se distorsionan. ¿Qué es exactamente esta distorsión? ¿Cómo lo conceptualizamos?

La idea no es realmente tan radical como podría parecer al principio. Podemos visualizar la estructura del espacio y el tiempo utilizando una gráfica con posición y tiempo en sus ejes. Estas gráficas ya son familiares, pero las vamos a ver de una manera ligeramente diferente. Antes, los usábamos para describir el movimiento de los objetos. La cuadrícula subyacente a la gráfica era meramente el escenario en el que los actores interpretaban sus papeles. Ahora el fondo llega al primer plano: es el tiempo y el espacio mismos los que estamos estudiando. No necesariamente necesitamos tener una línea o una curva dibujada en la parte superior de la cuadrícula para representar un objeto en particular. Podemos, por ejemplo, solo querer hablar de eventos, representados como puntos en la gráfica como en la figura a.

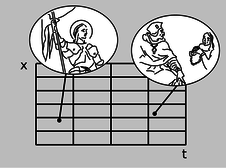
a/Dos eventos se dan como puntos en una gráfica de posición versus tiempo. Juana de Arco ayuda a restaurar a Carlos VII al trono. En un momento posterior y en una posición diferente, Juana de Arco es condenada a muerte.

Una distorsión de la cuadrícula cartesiana subyacente a la gráfica puede surgir por razones perfectamente ordinarias que Isaac Newton habría aceptado fácilmente. Por ejemplo, podemos simplemente cambiar las unidades utilizadas para medir el tiempo y la posición, como en la figura b.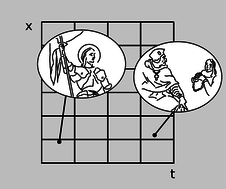

b/Un cambio de unidades distorsiona un\(x\) -\(t\) gráfico. Esta gráfica representa exactamente los mismos eventos que la figura a. El único cambio es que las\(t\) coordenadas\(x\) y se miden usando diferentes unidades, por lo que la cuadrícula se comprime\(t\) y expande en\(x\).

Vamos a tener bastantes ejemplos de este tipo, así que voy a adoptar la convención que se muestra en la figura c para representarlos. La figura c resume la relación entre las figuras a y b en una forma más compacta. El rectángulo gris representa la cuadrícula de coordenadas original de la figura a, mientras que la cuadrícula de líneas negras representa la nueva versión de la figura b. Omitir la cuadrícula del rectángulo gris hace que el diagrama sea más fácil de decodificar visualmente.

c/Una convención que usaremos para representar una distorsión del tiempo y del espacio.

Nuestro objetivo de desentrañar los misterios de la relatividad especial no equivale más que descubrir cómo dibujar un diagrama como c en el caso en que los dos conjuntos diferentes de coordenadas representan medidas de tiempo y espacio realizadas por dos observadores diferentes, cada uno en movimiento relativo al otro. Galileo y Newton pensaron que sabían la respuesta a esta pregunta, pero su respuesta resultó ser sólo aproximadamente correcta. Para evitar repetir los mismos errores, necesitamos explicar claramente cuáles creemos que son las propiedades básicas del tiempo y del espacio que serán una base confiable para nuestro razonamiento. Quiero enfatizar que no existe una manera puramente lógica de decidir sobre esta lista de propiedades. Los que voy a enumerar son simplemente un resumen de los patrones observados en los resultados de un gran cuerpo de experimentos. Además, algunos de ellos son sólo aproximados. Por ejemplo, la propiedad 1 a continuación es sólo una buena aproximación cuando el campo gravitacional es débil, por lo que es una propiedad que se aplica a la relatividad especial, no a la relatividad general.

Los experimentos muestran que:

1. Ningún punto en el tiempo o el espacio tiene propiedades que lo hacen diferente de cualquier otro punto.
2. Así mismo, todas las direcciones en el espacio tienen las mismas propiedades.
3. El movimiento es relativo, es decir, todos los marcos inerciales de referencia son igualmente válidos.
4. La causalidad se mantiene, en el sentido descrito en la página 381.
5. El tiempo depende del estado de movimiento del observador.

La mayoría de estos no son muy subversivos. Las propiedades 1 y 2 se remontan a la época en que Galileo y Newton comenzaron a aplicar las mismas leyes universales del movimiento al sistema solar y a la tierra; esto contradice a Aristóteles, quien creía que, por ejemplo, una roca naturalmente querría moverse en cierta dirección especial (abajo) para alcanzar una cierta ubicación especial (la superficie de la tierra). La propiedad 3 es la razón por la que Einstein llamó a su teoría “relatividad”, pero Galileo y Newton creían que exactamente lo mismo era cierto, como lo dramatizó el encuentro de Galileo con la Iglesia sobre la cuestión de si la tierra realmente podría estar en movimiento alrededor del sol. La propiedad 4 probablemente sorprendería a la mayoría de la gente sólo porque afirma de manera tan débil y especializada algo que sienten profundamente debe ser cierto. El único elemento realmente extraño de la lista es 5, pero el experimento de Hafele-Keating nos lo obliga.

d/Una versión galileana de la relación entre dos marcos de referencia. Como en todas esas gráficas de este capítulo, las coordenadas originales, representadas por el rectángulo gris, tienen un eje de tiempo que va hacia la derecha, y un eje de posición que va recto hacia arriba.

Si no fuera por la propiedad 5, podríamos imaginar que la figura d daría la correcta transformación entre marcos de referencia en movimiento relativos entre sí. Digamos que ese observador 1, cuya cuadrícula coincide con el rectángulo gris, es un autoestopista parado al costado de una carretera. El evento A es una gota de lluvia que le golpea la cabeza, y el evento B es otra gota de lluvia que le golpea la cabeza. Dice que A y B ocurren en la misma ubicación en el espacio. El observador 2 es un automovilista que pasa sin detenerse; para él, el habitáculo de su automóvil está en reposo, mientras que el asfalto se desliza por debajo. Dice que A y B ocurren en diferentes puntos del espacio, pues durante el tiempo entre la primera gota de lluvia y la segunda, el autoestopista se ha movido hacia atrás. Por otra parte, el observador 2 dice que los eventos A y C ocurren en el mismo lugar, mientras que el autoestopista no está de acuerdo. La pendiente de las líneas de la cuadrícula es simplemente la velocidad del movimiento relativo de cada observador en relación con el otro.

La figura d tiene un comportamiento familiar, reconfortante y eminentemente sensato, pero también resulta estar equivocado, porque viola la propiedad 5. La distorsión de la cuadrícula de coordenadas sólo ha movido las líneas verticales hacia arriba y hacia abajo, por lo que ambos observadores coinciden en que eventos como B y C son simultáneos. Si así fuera realmente la forma en que funcionaban las cosas, entonces todos los observadores podrían sincronizar todos sus relojes entre sí de una vez por todas, y los relojes nunca saldrían de sincronía. Esto contradice los resultados del experimento Hafele-Keating, en el que los tres relojes se sincronizaron inicialmente en Washington, pero más tarde se quedaron desincronizados debido a sus diferentes estados de movimiento.

Podría parecer que todavía teníamos una enorme cantidad de margen de maniobra disponible para la forma correcta de la distorsión. Resulta, sin embargo, que las propiedades 1-5 son suficientes para demostrar que sólo hay una respuesta, que es la que encontró Einstein en 1905. Para ver por qué es esto, trabajemos por un proceso de eliminación.

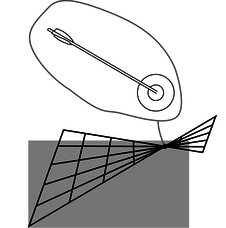
e/Una transformación que lleva a desacuerdos sobre si dos eventos ocurren al mismo tiempo y lugar. Esto no es sólo una cuestión de opinión. O la flecha golpeó el ojo de buey o no lo hizo.

La figura e muestra una transformación que puede parecer a primera vista ser un candidato tan bueno como cualquier otro, pero viola la propiedad 3, ese movimiento es relativo, por la siguiente razón. En el marco de referencia del observador 2, algunas de las líneas de la cuadrícula se cruzan entre sí. Esto significa que los observadores 1 y 2 no están de acuerdo sobre si ciertos eventos son iguales o no. Por ejemplo, supongamos que el evento A marca la llegada de una flecha al ojo de buey de un objetivo, y el evento B es la ubicación y la hora en que se perfora el ojo de buey. Los eventos A y B ocurren en el mismo lugar y al mismo tiempo. Si un observador dice que A y B coinciden, pero otro dice que no lo hacen, tenemos una contradicción directa. Dado que los dos marcos de referencia en la figura e dan resultados contradictorios, uno de ellos es correcto y otro incorrecto. Esto viola la propiedad 3, porque se supone que todos los marcos inerciales de referencia son igualmente válidos. Para evitar problemas como este, claramente necesitamos asegurarnos de que ninguna de las líneas de la cuadrícula se cruce alguna vez entre sí.

El siguiente tipo de transformación que queremos matar se muestra en la figura f, en la que las líneas de la cuadrícula se curvan, pero nunca se cruzan entre sí. El problema con éste es que viola la propiedad 1, la uniformidad del tiempo y el espacio. La transformación es inusualmente “torcida” en A, mientras que en B es mucho más suave. Esto no puede ser correcto, porque se supone que la transformación sólo depende del estado relativo de movimiento de los dos marcos de referencia, y esa información dada no destaca un papel especial para ningún punto particular en el espacio-tiempo. Si, por ejemplo, tuviéramos un marco de referencia girando con relación al otro, entonces habría algo especial sobre el eje de rotación. Pero aquí solo estamos hablando de marcos inerciales de referencia, como se especifica en la propiedad 3, por lo que no podemos tener rotación; cada marco de referencia tiene que estar moviéndose en línea recta a velocidad constante. Para los marcos relacionados de esta manera, no hay nada que pueda destacar un evento como A para un tratamiento especial en comparación con B, por lo que la transformación f viola la propiedad 1.

Los ejemplos de las figuras e y f muestran que la transformación que buscamos debe ser lineal, es decir, que debe transformar líneas en líneas, y además que tiene que tomar líneas paralelas a líneas paralelas. Einstein escribió en su artículo de 1905 que “... a causa de la propiedad de homogeneidad [propiedad 1] que atribuimos al tiempo y al espacio, la [transformación] debe ser lineal”. ¹ Aplicando esto a nuestros diagramas, el rectángulo gris original, que es un tipo especial de paralelogramo que contiene ángulos rectos, debe transformarse en otro paralelogramo. Hay tres tipos de transformaciones, la figura g, que tienen esta propiedad. El caso I es la transformación galileana de la figura d de la página 386, que ya descartamos.

g/Tres tipos de transformaciones que preservan el paralelismo. Su característica distintiva es lo que hacen a la simultaneidad, como lo demuestra lo que sucede con el borde izquierdo del rectángulo original. En I, el borde izquierdo permanece vertical, por lo que los eventos simultáneos permanecen simultáneos. En II, el borde izquierdo gira en sentido antihorario. En III, gira en sentido horario.

También se puede descartar el caso II. Aquí cada punto de la cuadrícula gira en sentido antihorario. ¿Qué parámetro físico determinaría la cantidad de rotación? Lo único que podría ser relevante sería\(v\), la velocidad relativa del movimiento de los dos marcos de referencia uno con respecto al otro. Pero si el ángulo de rotación era proporcional a\(v\), entonces para velocidades suficientemente grandes la cuadrícula habría invertido izquierda y derecha, y esto violaría la propiedad 4, causalidad: un observador diría que el evento A causó un evento posterior B, pero otro observador diría que B vino primero y causó A.

h/En las unidades que son más convenientes para la relatividad, la transformación tiene simetría alrededor de una línea diagonal de 45 grados.

La única posibilidad restante es el caso III, que he redibujado en la figura h con un par de cambios. Este es el que Einstein predijo en 1905. La transformación se conoce como la transformación de Lorentz, después de HendrikLorentz (1853-1928), quien anticipó parcialmente la obra de Einstein, sin llegar a la interpretación correcta. La distorsión es una especie de besos y estiramientos, como sugieren las manos. Además, ya hemos visto en las figuras a - c de la página 385 que somos libres de estirar o comprimir todo tanto como nos guste en las direcciones horizontal y vertical, porque esto simplemente corresponde a elegir diferentes unidades de medida para el tiempo y distancia. En la figura h he elegido unidades que dan a todo el dibujo una simetría conveniente alrededor de una línea diagonal de 45 grados. Normalmente no tendría sentido hablar de un ángulo de 45 grados en una gráfica cuyos ejes tuvieran diferentes unidades. Pero en la relatividad, la apariencia simétrica de la transformación nos dice que el espacio y el tiempo deben tratarse en pie de igualdad, y medirse en las mismas unidades.

i/Interpretación de la transformación de Lorentz. La pendiente indicada en la figura da la velocidad relativa de los dos marcos de referencia. Los eventos A y B que fueron simultáneos en el fotograma 1 no son simultáneos en el fotograma 2, donde el evento A ocurre a la derecha de la\(t=0\) línea representada por el borde izquierdo de la cuadrícula, sino que el evento B ocurre a su izquierda.

Al igual que en nuestra discusión sobre la transformación galileana, las pendientes se interpretan como velocidades, y la pendiente de las líneas casi horizontales en la figura i se interpreta como la velocidad relativa de los dos observadores. La diferencia entre la versión galileana y la relativista es que ahora también hay besos ocurriendo desde el otro lado. Las líneas que eran verticales en la cuadrícula original, que representan eventos simultáneos, ahora se inclinan hacia la derecha. Esto nos dice que, como lo exige la propiedad 5, diferentes observadores no están de acuerdo sobre si los eventos que ocurren en diferentes lugares son simultáneos. El experimento de Hafele-Keating nos dice que este efecto de no simultaneidad es bastante pequeño, incluso cuando la velocidad es tan grande como la de un jet de pasajeros, y esto es lo que hubiéramos anticipado por el principio de correspondencia. La forma en que esto se expresa en la gráfica es que si elegimos la unidad de tiempo para que sea la segunda, entonces la unidad de distancia resulta ser cientos de miles de millas. En estas unidades, la velocidad de un jet de pasajeros es un número extremadamente pequeño, por lo que la pendiente\(v\) en la figura i es extremadamente pequeña, y la cantidad de distorsión es pequeña —sería demasiado pequeña para verla en esta escala.

Lo único que queda por determinar sobre la transformación de Lorentz es el tamaño del paralelogramo transformado relativo al tamaño del original. Si bien el dibujo de las manos en la figura h puede sugerir que la rejilla se deforma como un armazón hecho de alambre rígido de percha, ese no es el caso. Si miras cuidadosamente la figura, verás que los bordes del paralelogramo suavizado son en realidad un poco más largos que los bordes del rectángulo original. De hecho lo que permanece igual no son longitudes sino áreas, como se demuestra en la leyenda a la figura j.

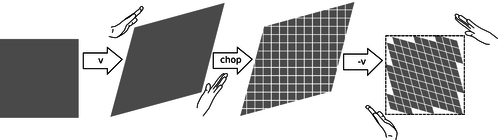
j/Prueba de que las transformaciones de Lorentz no cambian de área: Primero sometemos un cuadrado a una transformación con velocidad\(v\), y esto aumenta su área en un factor\(R(v)\), que queremos probar es igual a 1. Cortamos el paralelogramo resultante en pequeños cuadrados y finalmente aplicamos una\(-v\) transformación; esto cambia el área de cada pequeño cuadrado por un factor\(R(-v)\), por lo que el área de la figura completa también se escala por\(R(-v)\). El resultado final es restaurar el cuadrado a su forma y área originales, así\(R(v)R(-v)=1\). Pero\(R(v)=R(-v)\) por propiedad 2 del espacio-tiempo en la página 385, que establece que todas las direcciones en el espacio tienen las mismas propiedades, entonces\(R(v)=1\).

7.2.2 El\(\gamma\) factor

Con un poco de álgebra y geometría (problema de tarea 7, página 439), se puede usar la propiedad de área igual para mostrar que el factor\(\gamma\) (letra griega gamma) definido en la figura k viene dado por la ecuación

\[\begin{equation*} \gamma = \frac{1}{\sqrt{1-v^2}} . \end{equation*}\]

Si has tenido una buena formación en física, lo primero que probablemente piensas cuando miras esta ecuación es que debe ser una tontería, porque sus unidades no tienen sentido. ¿Cómo podemos tomar algo con unidades de velocidad al cuadrado, y restarlo de un 1 sin unidades? Pero recuerde que esto se expresa en nuestras unidades relativistas especiales, en las que se utilizan las mismas unidades para la distancia y el tiempo. En este sistema, las velocidades son siempre sin unidades. Este tipo de cosas ocurren con frecuencia en la física. Por ejemplo, antes de que James Joule descubriera la conservación de la energía, nadie sabía que el calor y la energía mecánica eran diferentes formas de lo mismo, así que en lugar de medirlos tanto en unidades de julios como lo haríamos ahora, midieron calor en una unidad (como calorías) y energía mecánica en otra (tal como pie-libras). En unidades métricas ordinarias, solo necesitamos un factor de conversión adicional\(c\), y la ecuación se convierte en

\[\begin{equation*} \gamma = \frac{1}{\sqrt{1-\left(\frac{v}{c}\right)^2}} . \end{equation*}\]

He aquí por qué nos importa\(\gamma\). La figura k la define como la relación de dos veces: el tiempo entre dos eventos expresado en un sistema de coordenadas, y el tiempo entre los mismos dos eventos medidos en el otro. La interpretación es:

k/El\(\gamma\) factor.

Dilatación del tiempo

Un reloj corre más rápido en el marco de referencia de un observador que está en reposo en relación con el reloj. Un observador en movimiento relativo al reloj a velocidad\(v\) percibe que el reloj corre más lentamente por un factor de\(\gamma\).

Como se demuestra en las figuras l y m, las longitudes también están distorsionadas:

l/La regla se mueve en el cuadro 1, representado por un cuadrado, pero en reposo en el cuadro 2, mostrado como un paralelogramo. Cada imagen de la regla es una instantánea tomada en un momento determinado según se juzga de acuerdo con la noción de simultaneidad del marco 2. Un observador en el cuadro 1 juzga la longitud de la regla según la definición de simultaneidad del fotograma 1, es decir, usando puntos alineados verticalmente en la gráfica. La regla aparece más corta en el marco en el que se mueve. Como se demuestra en la figura m, la duración se contrae desde\(L\) hasta\(L/\gamma\).

m/Esta cifra demuestra, como se afirma en la figura l, que la contracción de longitud es\(x=1/\gamma\). Primero cortamos el paralelogramo verticalmente como un salami y deslizamos las rebanadas hacia abajo, haciendo horizontales los bordes superior e inferior. Entonces hacemos lo mismo en la dirección horizontal, formando un rectángulo con lados\(\gamma\) y\(x\). Dado que tanto los procesos de transformación de Lorentz como los procesos de corte dejan las áreas sin cambios, el área\(\gamma x\) del rectángulo debe ser igual al área del cuadrado original, que es 1.

Contracción de longitud

Un medidor de palo aparece más largo para un observador que está en reposo relativo a él. Un observador que se mueve en relación con el medidor de varilla en\(v\) observa el palo para ser acortado por un factor de\(\gamma\).

Ejercicio\(\PageIndex{1}\)

¿Qué es\(\gamma\) cuándo\(v=0\)? ¿Qué significa esto?

(respuesta en la parte posterior de la versión PDF del libro)

Ejemplo\(\PageIndex{1}\): An interstellar road trip

Alice se queda en la tierra mientras su gemela Betty se dirige en una nave espacial a Tau Ceti, una estrella cercana. Tau Ceti está a 12 años luz de distancia, así que a pesar de que Betty viaja al 87% de la velocidad de la luz, le llevará mucho tiempo llegar allí: 14 años, según Alice.

n/Ejemplo 1.

Betty experimenta dilatación del tiempo. A esta velocidad, ella\(\gamma\) es 2.0, por lo que el viaje sólo le parecerá durar 7 años. Pero hay una simetría perfecta entre los marcos de referencia de Alice y Betty, por lo que Betty coincide con Alice en su velocidad relativa; Betty se ve a sí misma como en reposo, mientras que el sol y Tau Ceti se mueven hacia atrás al 87% de la velocidad de la luz. ¿Cómo, entonces, puede observar a Tau Ceti para llegar a ella en solo 7 años, cuando debería tomar 14 años viajar 12 años luz a esta velocidad?

Tenemos que tener en cuenta la contracción de longitud. Betty ve que la distancia entre el sol y Tau Ceti se reduce en un factor de 2. Lo mismo ocurre para Alice, quien observa que Betty y su nave espacial sean escorzadas.

Ejemplo\(\PageIndex{2}\): Large time dilation

El efecto de dilatación del tiempo en el experimento de Hafele-Keating fue muy pequeño. Si queremos ver un gran efecto de dilatación en el tiempo, no podemos hacerlo con algo del tamaño de los relojes atómicos que usaron; la energía cinética sería mayor que el megatonaje total de todos los arsenales nucleares del mundo. Podemos, sin embargo, acelerar las partículas subatómicas a velocidades a las que\(\gamma\) es grande. Para los físicos experimentales de partículas, la relatividad es algo que haces todo el día antes de volver a casa y hacer una parada en la tienda de leche. Un experimento temprano de baja precisión de este tipo fue realizado por Rossi y Hall en 1941, utilizando rayos cósmicos naturales. La Figura p muestra un experimento ² de 1974 de tipo similar que verificó la dilatación temporal predicha por la relatividad con una precisión de aproximadamente una parte por mil.

Las partículas llamadas muones (que llevan el nombre de la letra griega\(\mu\), “myoo”) fueron producidas por un acelerador en el CERN, cerca de Ginebra. Un muón es esencialmente una versión más pesada del electrón. Los muones sufren desintegración radiactiva, durando un promedio de sólo 2.197\(\mu\text{s}\) antes de evaporarse en un electrón y dos neutrinos. El experimento de 1974 fue construido para medir las propiedades magnéticas de los muones, pero produjo una prueba de alta precisión de dilatación del tiempo como subproducto. Debido a que los muones tienen la misma carga eléctrica que los electrones, pueden quedar atrapados usando campos magnéticos. Los muones fueron inyectados en el anillo que se muestra en la figura p, dando vueltas alrededor de él hasta que sufrieron desintegración radiactiva. A la velocidad a la que viajaban estos muones, lo tenían\(\gamma=29.33\), por lo que en promedio duraron 29.33 veces más que la vida normal. En otras palabras, eran como diminutos despertadores que se autodestruían a una hora seleccionada al azar. La figura o muestra el número de desintegraciones radiactivas contadas, en función del tiempo transcurrido después de que se inyectara una determinada corriente de muones en el anillo de almacenamiento. Las dos líneas discontinuas muestran las tasas de decaimiento predichas con y sin relatividad. La línea relativista es la que concuerda con el experimento.

o/Los muones aceleraron para casi\(c\) sufrir desintegración radiactiva mucho más lentamente de lo que lo harían según un observador en reposo con respecto a los muones. Los dos primeros puntos de datos (círculos sin relleno) fueron sometidos a grandes errores sistemáticos.

p/Aparato utilizado para la prueba de dilatación relativista del tiempo descrita en el ejemplo 2. Los bloques prominentes en blanco y negro son grandes imanes que rodean una tubería circular con vacío en su interior. c) 1974 por el CERN.

Ejemplo\(\PageIndex{3}\): An example of length contraction

La figura q muestra la representación de un artista de la contracción de longitud para la colisión de dos núcleos de oro a velocidades relativistas en el acelerador RHIC en Long Island, Nueva York, que salió en línea en el año 2000. Los núcleos de oro aparecerían casi esféricos (o apenas ligeramente alargados como un balompié americano) en marcos que se mueven junto con ellos, pero en el marco del laboratorio, ambos aparecen drásticamente acortados a medida que se acercan al punto de colisión. Las imágenes posteriores muestran los núcleos fusionándose para formar una sopa caliente, en la que los experimentadores esperan observar una nueva forma de materia.

q/Núcleos colisionantes muestran contracción relativista de longitud.

Ejemplo\(\PageIndex{1}\): The garage paradox

Una de las más famosas de todas las llamadas paradojas de la relatividad tiene que ver con nuestro sentimiento incorrecto de que la simultaneidad está bien definida. La idea es que uno pueda tomar un autobús escolar y conducirlo a velocidades relativistas a un garaje de tamaño ordinario, en el que normalmente no cabría. Debido a la contracción de longitud, el autobús supuestamente cabría en la cochera. El chofer, sin embargo, percibirá la cochera como contratada y por lo tanto aún menos capaz de contener el autobús.

La paradoja se resuelve cuando reconocemos que el concepto de encajar el autobús en el garaje “todo a la vez” contiene una suposición oculta, la suposición de que tiene sentido preguntar si la parte delantera y trasera del autobús pueden estar simultáneamente en la cochera. Los observadores en diferentes marcos de referencia que se mueven a altas velocidades relativas no necesariamente están de acuerdo sobre si las cosas suceden simultáneamente. Como se muestra en la figura r, la persona en el marco del garaje puede cerrar la puerta en un instante B percibe que es simultánea con la llegada del parachoques delantero A a la pared trasera del garaje, pero el conductor no estaría de acuerdo sobre la simultaneidad de estos dos eventos, y percibiría que la puerta tenía cerró mucho después de que atravesara la pared posterior.

r/Ejemplo 4: En el marco de referencia del garaje, el autobús se mueve, y puede caber en el garaje debido a su contracción de longitud. En el marco de referencia del autobús, el garaje se mueve, y no puede sostener el autobús debido a su contracción de longitud.

7.2.3 La velocidad universal\(c\)

Pensemos un poco más en el papel de la diagonal de 45 grados en la transformación de Lorentz. Las pendientes en estas gráficas se interpretan como velocidades. Esta línea tiene una pendiente de 1 en unidades relativistas, pero esa pendiente corresponde a\(c\) en unidades métricas ordinarias. Ya sabemos que la unidad de distancia relativista debe ser extremadamente grande en comparación con la unidad de tiempo relativista, por lo que\(c\) debe ser extremadamente grande. Ahora note lo que sucede cuando realizamos una transformación de Lorentz: esta línea en particular se estira, pero la nueva versión de la línea se encuentra justo encima de la antigua, y su pendiente permanece igual. En otras palabras, si un observador dice que algo tiene una velocidad igual a\(c\), todos los demás observadores también estarán de acuerdo en esa velocidad. (Lo mismo sucede con\(-c\).)

Las velocidades no se limitan a sumar y restar.

Esto es contradictorio, ya que esperamos que las velocidades sumen y resten en movimiento relativo. Si un perro está huyendo de mí a 5 m/s con relación a la acera, y corro tras ella a 3 m/s, la velocidad del perro en mi marco de referencia es de 2 m/s Según todo lo que hayamos aprendido sobre el movimiento, el perro debe tener diferentes velocidades en los dos cuadros: 5 m/s en el marco de la acera y 2 m/s en el mío. Pero las velocidades se miden dividiendo una distancia por un tiempo, y tanto la distancia como el tiempo se distorsionan por efectos relativistas, por lo que en realidad no deberíamos esperar que la adición aritmética ordinaria de velocidades se mantenga en la relatividad; es una aproximación que es válida a velocidades que son pequeñas en comparación con \(c\).

Un límite de velocidad universal

Por ejemplo, supongamos que Janet realiza un viaje en una nave espacial, y acelera hasta que se mueve en\(0.6c\) relación con la tierra. Luego lanza una sonda espacial en la dirección de avance a una velocidad relativa a su nave de\(0.6c\). Podríamos pensar que la sonda se movía entonces a una velocidad de\(1.2c\), pero de hecho la respuesta sigue siendo menor que\(c\) (problema 1, página 438). Este es un ejemplo de un hecho más general sobre la relatividad, que es que\(c\) representa un límite de velocidad universal. Esto es requerido por la causalidad, como se muestra en la figura s.

s/Una prueba de que la causalidad impone un límite de velocidad universal. En el marco de referencia original, representado por el cuadrado, el evento A ocurre un poco antes del evento B. En el nuevo marco, mostrado por el paralelogramo, A ocurre después\(t=0\), pero B ocurre antes\(t=0\); es decir, B ocurre antes de A. Se ha invertido el orden de tiempo de los dos eventos. Esto sólo puede suceder porque los eventos A y B están muy unidos en el tiempo y bastante separados en el espacio. El segmento de línea que conecta A y B tiene una pendiente mayor a 1, lo que significa que si quisiéramos estar presentes en ambos eventos, tendríamos que viajar a una velocidad mayor que\(c\) (lo que equivale a 1 en las unidades utilizadas en esta gráfica). Encontrarás que si eliges dos puntos cualesquiera para los que la pendiente del segmento de línea que los conecta sea menor que 1, nunca podrás conseguir que se monten a horcajadas sobre la nueva\(t=0\) línea de esta manera divertida y invertida en el tiempo. Dado que diferentes observadores no están de acuerdo en el orden temporal de eventos como A y B, la causalidad requiere que la información nunca viaje de A a B o de B a A; si lo hiciera, entonces tendríamos paradojas de viajes en el tiempo. La conclusión es que\(c\) es la velocidad máxima de causa y efecto en la relatividad.

t/El experimento de Michelson-Morley, mostrado en fotografías, y dibujos del papel original de 1887. 1. Un dibujo simplificado del aparato. Un haz de luz de la fuente, s, es parcialmente reflejado y transmitido parcialmente por el espejo semiplateado\(\text{h}_1\). Las dos partes de media intensidad del haz son reflejadas por los espejos en a y b, reunidas y observadas en el telescopio, t. Si se suponía que la superficie de la tierra se movía a través del éter, entonces los tiempos que tomaban las dos ondas de luz para pasar a través del éter móvil serían desiguales, y el tiempo resultante el retraso sería detectable observando la interferencia entre las ondas cuando se reunieran. 2. En el aparato real, los haces de luz se reflejaron múltiples veces. La longitud efectiva de cada brazo se incrementó a 11 metros, lo que mejoró en gran medida su sensibilidad a la pequeña diferencia esperada en la velocidad de la luz. 3. En una versión anterior del experimento, se habían topado con problemas por su “extrema sensibilidad a la vibración”, que era “tan grande que era imposible ver las franjas de interferencia excepto a intervalos breves... incluso a las dos de la mañana”. Por lo tanto, montaron todo sobre una piedra masiva que flotaba en una charca de mercurio, lo que también hizo posible girarla fácilmente. 4. Una foto del aparato.

La luz viaja a\(c\).

Ahora considera un haz de luz. Estamos acostumbrados a hablar casualmente sobre la “velocidad de la luz”, pero ¿qué significa eso en realidad? El movimiento es relativo, así que normalmente si queremos hablar de una velocidad, tenemos que especificar a qué se mide en relación. Una onda de sonido tiene cierta velocidad en relación con el aire, y una ola de agua tiene su propia velocidad en relación con el agua. Si queremos medir la velocidad de una ola oceánica, por ejemplo, debemos asegurarnos de medirla en un marco de referencia en reposo relativo al agua. Pero la luz no es una vibración de un medio físico; puede propagarse a través del vacío casi perfecto del espacio exterior, como cuando los rayos de luz solar viajan a la tierra. Esto parece una paradoja: se supone que la luz tiene una velocidad específica, pero no hay forma de decidir en qué marco de referencia medirla. La salida de la paradoja es que la luz debe viajar a una velocidad igual a\(c\). Ya que todos los observadores coinciden en una velocidad de\(c\), independientemente de su marco de referencia, todo es consistente.

El experimento de Michelson-Morley

La constancia de la velocidad de la luz de hecho ya se había observado cuando Einstein era un niño de 8 años, pero debido a que nadie podía entender cómo interpretarla, el resultado fue ignorado en gran medida. En 1887 Michelson y Morley instalaron un aparato inteligente para medir cualquier diferencia en la velocidad de los haces de luz que viajan de este-oeste y norte-sur. El movimiento de la tierra alrededor del sol a 110.000 km/hora (aproximadamente 0.01% de la velocidad de la luz) es hacia nuestro oeste durante el día. Michelson y Morley creían que la luz era una vibración de un misterioso medio llamado el éter, por lo que esperaban que la velocidad de la luz fuera un valor fijo relativo al éter. A medida que la tierra se movía a través del éter, pensaron que observarían un efecto en la velocidad de la luz a lo largo de una línea este-oeste. Por ejemplo, si soltaban un haz de luz en dirección oeste durante el día, esperaban que se alejaría de ellos a una velocidad inferior a la normal porque la tierra la perseguía a través del éter. Se sorprendieron cuando encontraron que no se produjo el cambio esperado de 0.01% en la velocidad de la luz.

Ejemplo\(\PageIndex{4}\): The ring laser gyroscope

Si has volado en un avión jet, puedes agradecerle a la relatividad por ayudarte a evitar chocar contra una montaña o un océano. La figura u muestra una pieza estándar de equipo de navegación llamada giroscopio láser anular. Un haz de luz se divide en dos partes, se envía alrededor del perímetro del dispositivo y se reúne. Dado que la velocidad de la luz es constante, esperamos que las dos partes vuelvan a juntarse al mismo tiempo. Si no lo hacen, es evidencia de que el dispositivo ha estado rotando. La computadora del avión detecta esto y anota cuánta rotación se ha acumulado.

giroscopio láser de anillo u/A.

Ejemplo\(\PageIndex{6}\): No frequency-dependence

La relatividad solo tiene una velocidad universal, por lo que requiere que todas las ondas de luz viajen a la misma velocidad, independientemente de su frecuencia y longitud de onda. Actualmente las mejores pruebas experimentales de la invarianza de la velocidad de la luz con respecto a la longitud de onda provienen de observaciones astronómicas de ráfagas de rayos gamma, que son emanaciones repentinas de luz de alta frecuencia, que se cree que se originan a partir de una explosión de supernova en otra galaxia. Una de esas observaciones, en 2009, ³ encontró que los tiempos de llegada de todas las diferentes frecuencias en la ráfaga diferían en no más de 2 segundos de un tiempo total en vuelo del orden de ¡diez mil millones de años!

Preguntas de Discusión

◊ Una persona en una nave espacial que se mueve al 99.99999999% de la velocidad de la luz relativa a la Tierra hace brillar una linterna hacia adelante a través del aire polvoriento, por lo que el haz es visible. ¿Qué ve ella? ¿Qué le parecería a un observador en la Tierra?

◊

Pregunta de discusión B.

Una pregunta con la que los estudiantes a menudo luchan es si el tiempo y el espacio realmente pueden distorsionarse, o si simplemente parece así. Compara con ilusiones ópticas o trucos de magia. ¿Cómo se pudo verificar, por ejemplo, que las líneas de la figura son en realidad paralelas? ¿Los efectos relativistas son los mismos, o no?

◊ En una nave espacial que se mueve a velocidades relativistas, ¿una conferencia parecería aún más larga y más aburrida de lo normal?

◊ Los relojes mecánicos pueden verse afectados por el movimiento. Por ejemplo, fue un logro tecnológico significativo construir un reloj que pudiera navegar a bordo de un barco y aún así mantener la hora exacta, permitiendo determinar la longitud. ¿Cómo es esto similar o diferente de la dilatación relativista del tiempo?

◊ La figura q de la página 392, que representa la colisión de dos núcleos en el acelerador RHIC, se reproduce a continuación. ¿Cómo serían las formas de los dos núcleos para un observador microscópico montado sobre el núcleo izquierdo? ¿A un observador cabalgando en el de la derecha? ¿Pueden ponerse de acuerdo en lo que está pasando? Si no, ¿por qué no? Después de todo, ¿no deberían ver lo mismo si ambos comparan los dos núcleos uno al lado del otro en el mismo instante en el tiempo?

v/Pregunta de discusión E: núcleos colisionantes muestran contracción relativista de longitud.

◊ Si metes un trozo de gomaespuma por la ventana de tu auto mientras conduces por la autopista, el viento puede comprimirlo un poco. ¿Tiene sentido interpretar la contracción relativista de longitud como un tipo de tensión que empuja así los átomos de un objeto juntos? ¿Cómo se relaciona esto con la pregunta de discusión E?

◊ El ametrallador en la figura envía un chorro de balas. Supongamos que las balas están siendo disparadas al espacio exterior, y que las distancias recorridas son de billones de millas (para que la figura humana en el diagrama no esté a escala). Después de mucho tiempo, las balas llegan a los puntos mostrados con puntos que están todos igualmente lejos del arma. Sus llegadas a esos puntos son eventos de la A a la E, que ocurren en diferentes momentos. La cadena de impactos se extiende a través del espacio a una velocidad mayor que\(c\). ¿Esto viola la relatividad especial?

Pregunta de discusión G.

7.2.4 Sin acción a distancia

El panorama newtoniano

La imagen newtoniana del universo tiene partículas que interactúan entre sí ejerciendo fuerzas desde la distancia, y se imagina que estas fuerzas ocurren sin ningún retraso de tiempo. Por ejemplo, supongamos que extraterrestres superpoderosos, enfurecidos cuando escuchan música disco en nuestras transmisiones de radio AM, llegan a nuestro sistema solar con la misión de limpiar el universo de nuestra contaminación estética. Aplican una fuerza a nuestro sol, lo que hace que salga volando del sistema solar a miles de millones de kilómetros por hora. Según las leyes de Newton, la fuerza gravitacional del sol sobre la tierra comenzará a caer de inmediato. Esto será detectable en la tierra, y dado que la luz solar tarda ocho minutos en llegar del sol a la tierra, el cambio en la fuerza gravitacional será, según Newton, la primera forma en que los terrícolas aprendan las malas noticias —el sol no comenzará visiblemente a retroceder hasta un poco más tarde. Si bien este escenario es fantasioso, muestra una característica real de las leyes de Newton: que la información puede transmitirse de un lugar del universo a otro con retardo de tiempo cero, de manera que la transmisión y recepción ocurren exactamente en el mismo instante. Newton fue lo suficientemente agudo como para darse cuenta de que esto requería una suposición no trivial, que era que había alguna manera completamente objetiva y bien definida de decir si dos cosas sucedieron exactamente en el mismo instante. Afirmó esta suposición explícitamente: “El tiempo absoluto, verdadero y matemático, de sí mismo, y de su propia naturaleza fluye a un ritmo constante sin tener en cuenta nada externo...”

Retrasos de tiempo en las fuerzas ejercidas a distancia

La relatividad prohíbe la acción instantánea de Newton a distancia. Por suponer que existía una acción instantánea a distancia. Entonces sería posible enviar señales de un lugar del universo a otro sin ningún retraso de tiempo. Esto permitiría una perfecta sincronización de todos los relojes. Pero el experimento de Hafele-Keating demuestra que los relojes A y B que se han sincronizado inicialmente se desviarán de sincronía si uno está en movimiento relativo al otro. Con transmisión instantánea de señales, pudimos determinar, sin tener que esperar a que A y B se reunieran, cuál estaba adelante y cuál estaba detrás. Ya que no necesitan ser reunidos, ninguno necesita sufrir ninguna aceleración; cada reloj puede fijar un marco inercial de referencia, con un vector de velocidad que no cambia ni su dirección ni su magnitud. Pero esto viola el principio de que el movimiento de velocidad constante es relativo, porque cada reloj puede considerarse en reposo, en su propio marco de referencia. Dado que ningún experimento ha detectado alguna violación de la relatividad del movimiento, concluimos que la acción instantánea a distancia es imposible.

Dado que las fuerzas no pueden transmitirse instantáneamente, se vuelve natural imaginar los efectos de fuerza extendiéndose hacia afuera desde su fuente como ondas en un estanque, y entonces no tenemos más remedio que imputar alguna realidad física a estas ondas. Nosotros los llamamos campos, y ellos tienen su propia existencia independiente. La gravedad se transmite a través de un campo llamado campo gravitacional. Además de la gravedad, existen otros campos fundamentales de fuerza como la electricidad y el magnetismo (ch. 10 - 11). Ondas de los campos eléctrico y magnético resultan ser ondas de luz. Esto nos dice que la velocidad a la que se propagan las ondas de campo eléctrico y magnético debe ser\(c\), y por un argumento similar al de la subsección 7.2.3 debe sostenerse lo mismo para cualquier otro campo fundamental, incluido el campo gravitacional.

Los campos no tienen que menearse; también pueden quedarse quietos. El campo magnético de la tierra, por ejemplo, es casi constante, por lo que podemos usarlo para encontrar la dirección.

Incluso el espacio vacío, entonces, no es perfectamente carente de rasgos. Tiene propiedades medibles. Por ejemplo, podemos dejar caer una roca para medir la dirección del campo gravitacional, o usar una brújula magnética para encontrar la dirección del campo magnético. Este concepto causó una profunda impresión en Einstein cuando era niño. Recordó que cuando tenía cinco años, el don de una brújula magnética le convenció de que había “algo detrás de las cosas, algo profundamente oculto”.

Más evidencia de que los campos de fuerza son reales: portan energía.

w/Los campos llevan energía.

El argumento del fumador-arma para esta extraña noción de ondas de fuerza viajera proviene del hecho de que transportan energía. En la figura x /1, Alice y Betty sostienen las bolas A y B a cierta distancia entre sí. Estas bolas hacen fuerza unas sobre otras; en realidad no importa por el bien de nuestro argumento si esta fuerza es gravitacional, eléctrica o magnética. Digamos que es eléctrico, es decir, que las bolas tengan el tipo de carga eléctrica que a veces hace que tus calcetines se aferren cuando salen de la secadora de ropa. Diremos que la fuerza es repulsiva, aunque de nuevo realmente no importa.

x/Pregunta de discusión E.

Si Alice opta por acercar su pelota a Betty's, x /2, Alice tendrá que hacer algún trabajo mecánico contra la repulsión eléctrica, quemando algunas de las calorías de esa tarta de queso de chocolate que comió en el almuerzo. Esta reducción en la energía química de su cuerpo se compensa con un aumento correspondiente en la energía de interacción eléctrica. No sólo eso, sino que Alice siente que la resistencia se endurece a medida que las bolas se acercan y la repulsión se fortalece. Ella tiene que hacer un poco de trabajo extra, pero todo esto está debidamente contabilizado en la energía de interacción.

Pero ahora supongamos, x /3, que Betty decide jugarle una mala pasada a Alice lanzando a B muy lejos justo cuando Alice se prepara para moverse A. Ya hemos establecido que Alice no puede sentir el movimiento de B instantáneamente, por lo que las fuerzas eléctricas en realidad deben ser propagadas por un campo eléctrico. Por supuesto que este experimento es totalmente poco práctico, pero supongamos por el bien del argumento que el tiempo que tarda el cambio en el campo eléctrico para propagarse a través del diagrama es lo suficientemente largo para que Alice pueda completar su movimiento antes de que sienta el efecto de la desaparición de B. Ella todavía está recibiendo información obsoleta sobre la posición de B. Al mover A hacia la derecha, siente una repulsión, porque el campo en su región del espacio sigue siendo el campo causado por B en su antigua posición. Ella ha quemado algunas calorías de tarta de queso de chocolate, y parece que se ha violado la conservación de energía, debido a que estas calorías no pueden ser debidamente contabilizadas por ninguna interacción con B, que se ha ido hace mucho tiempo.

Si esperamos preservar la ley de conservación de la energía, entonces la única conclusión posible es que el propio campo eléctrico se lleva la energía del pastel de queso. De hecho, este ejemplo representa un método poco práctico de transmisión de ondas de radio. Alice sí trabaja en la carga A, y esa energía entra en las ondas de radio. Aunque B nunca hubiera existido, las ondas de radio seguirían llevando energía, y Alice habría tenido que trabajar para crearlas.

Preguntas de Discusión

◊ Amy y Bill están volando en naves espaciales en direcciones opuestas a velocidades tan altas que el efecto relativista sobre la velocidad de flujo del tiempo es fácilmente perceptible. La moción es relativa, por lo que Amy se considera a sí misma en reposo y Bill en movimiento. Dice que el tiempo fluye normalmente para ella, pero Bill es lento. Pero Bill puede decir exactamente lo mismo. ¿Cómo pueden pensar ambos que el otro es lento? ¿Pueden resolver el desacuerdo poniéndose en la radio y viendo de quién es la voz normal y cuyos sonidos se ralentizaron y Darth-Vadery?

◊ La figura muestra un famoso experimento pensativo ideado por Einstein. Un tren se mueve a velocidad constante hacia la derecha cuando relámpagos golpean el suelo cerca de su parte delantera y trasera. Alice, de pie sobre la suciedad en el punto medio de los destellos, observa que la luz de los dos destellos llega simultáneamente, por lo que dice que los dos golpes debieron haber ocurrido simultáneamente. Bob, por su parte, está sentado a bordo del tren, en su centro. Pasa junto a Alice en el momento en que luego Alice se da cuenta de que ocurrieron los destellos. Posteriormente, recibe flash 2, y luego flash 1. Infiere que dado que ambos flashes viajaron a la mitad de la longitud del tren, el flash 2 debió haber ocurrido primero. ¿Cómo se puede conciliar esto con la creencia de Alice de que los destellos eran simultáneos? Explique usando una gráfica.

◊ Resuelve la siguiente paradoja dibujando un diagrama de espacio-tiempo (es decir, una gráfica de\(x\) versus \(t\)). Andy and Beth are in motion relative to one another at a significant fraction of \(c\). As they pass by each other, they exchange greetings, and Beth tells Andy that she is going to blow up a stick of dynamite one hour later. One hour later by Andy's clock, she still hasn't exploded the dynamite, and he says to himself, “She hasn't exploded it because of time dilation. It's only been 40 minutes for her.” He now accelerates suddenly so that he's moving at the same velocity as Beth. The time dilation no longer exists. If he looks again, does he suddenly see the flash from the explosion? How can this be? Would he see her go through 20 minutes of her life in fast-motion?

◊ Usa una gráfica para resolver la siguiente paradoja de la relatividad. Relatividad dice que en un marco de referencia, el evento A podría suceder antes del evento B, pero en el marco B de otra persona vendría antes de A. ¿Cómo puede ser esto? Obviamente las dos personas podrían reunirse en A y platicar mientras cruzaban el uno al otro. ¿No tendrían que ponerse de acuerdo sobre si ya había sucedido B?

◊ La varilla en la figura es perfectamente rígida. En el evento A, el martillo golpea un extremo de la varilla. En el evento B, el otro extremo se mueve. Dado que la varilla es perfectamente rígida, no puede comprimirse, por lo que A y B son simultáneas. En el cuadro 2, B pasa antes que A. ¿El movimiento en el extremo derecho provocó que la persona de la izquierda decidiera levantar el martillo y usarlo?

7.2.5 El cono de luz

y/El cono de luz.

Dado un evento P, ahora podemos clasificar todas las relaciones causales en las que P puede participar. En la física newtoniana, estas relaciones se dividieron en dos clases: P podría potencialmente causar cualquier evento que estuviera en su futuro, y podría haber sido causado por cualquier evento en su pasado. En relatividad, tenemos una distinción de tres vías en lugar de una de dos vías. Hay una tercera clase de eventos que están demasiado lejos de P en el espacio, y demasiado cerca en el tiempo, para permitir cualquier relación de causa y efecto, ya que la velocidad máxima de la causalidad es\(c\). Ya que estamos trabajando en unidades en las que\(c=1\), el límite de este conjunto está formado por las líneas con pendiente\(\pm1\) en una\((t,x)\) parcela. Esto se conoce como el cono de luz, por razones que se vuelven más obvias visualmente cuando consideramos más de una dimensión espacial, figura aa.

aa/Ejemplo 9.

Se dice que los eventos que se encuentran dentro de los conos de luz del otro tienen una relación de tiempo. Los eventos fuera de los conos de luz de cada uno son espaciales en relación entre sí, y en el caso en que se encuentran en las superficies de los conos de luz de los demás, el término es parecido a la luz. \ subsección miopcional[ 2] {El intervalo espacio-tiempo}

El cono de luz es un objeto de importancia central tanto en la relatividad especial como en la general. Relaciona la geometría del espacio-tiempo con posibles relaciones de causa y efecto entre eventos. Así es fundamentalmente como funciona la relatividad: es una teoría geométrica de la causalidad.

Estas ideas nos llevan naturalmente a preguntarnos qué fructíferas analogías podemos formar entre la extraña geometría del espacio-tiempo y la geometría más familiar del plano euclidiano. El cono de luz corta el espacio-tiempo en diferentes regiones de acuerdo con ciertas mediciones de relaciones entre puntos (eventos). De igual manera, un círculo en geometría euclidiana corta el plano en dos partes, una interior y una exterior, según la medida de la distancia desde el centro del círculo. Un círculo permanece igual cuando giramos el plano. Un cono de luz permanece igual cuando cambiamos los marcos de referencia. Construyamos la analogía de manera más explícita.

Medición en geometría euclidiana

Decimos que dos segmentos de línea son congruentes\(\text{AB}\cong \text{CD}\),, si la distancia entre los puntos A y B es la misma que la distancia entre C y D, medida por una regla rígida.

Medición en espacio-tiempo

Definimos\(\text{AB}\cong \text{CD}\) si:

1. AB y CD son espaciales, y las dos distancias son iguales según se mide con una regla rígida, en un marco donde los dos eventos tocan la regla simultáneamente.
2. AB y CD son similares al tiempo, y los dos intervalos de tiempo son iguales según lo medido por los relojes que se mueven inercialmente.
3. AB y CD son parecidos a la luz.

Las tres partes de la versión relativista requieren cada una cierta justificación.

El caso 1 tiene que ser como es porque el espacio es parte del espacio-tiempo. En especial relatividad, este espacio es euclidiano, por lo que la definición de congruencia tiene que concordar con la definición euclidiana, en el caso de que sea posible aplicar la definición euclidiana. La relación espacial entre los puntos es necesaria y suficiente para que esto sea posible. Si los puntos A y B son espaciosos en relación entre sí, entonces existe un marco de referencia en el que son simultáneos, por lo que podemos usar una regla que esté en reposo en ese marco para medir su distancia. Si son similares a la luz o al tiempo, entonces no existe tal marco de referencia. Por ejemplo, no existe un marco de referencia en el que la restauración de Carlos VII al trono sea simultánea con la ejecución de Juana de Arco, por lo que no podemos hacer arreglos para que ambos eventos toquen al mismo gobernante al mismo tiempo.

La definición en el caso 2 es la única manera sensata de proceder si queremos respetar el tratamiento simétrico del tiempo y el espacio en la relatividad. La relación temporal entre los eventos es necesaria y suficiente para hacer posible que un reloj se mueva de uno a otro. Hace la diferencia que los relojes se muevan inercialmente, porque los gemelos del ejemplo 1 en la p. 391 no están de acuerdo en la hora del reloj entre la salida y el regreso del gemelo viajero.

El caso 3 puede parecer extraño, ya que dice que dos intervalos similares a la luz cualesquiera son congruentes. Pero esta es la única definición posible, porque este caso se puede obtener como un límite del tiempocomo uno. Supongamos que AB es un intervalo parecido al tiempo, pero en el marco de referencia del planeta tierra sería necesario viajar casi a la velocidad de la luz para llegar a B desde A. La velocidad requerida es menor que\(c\) (es decir, menor que 1) en alguna cantidad minúscula\(\epsilon\). En el marco de la tierra, el reloj al que se hace referencia en la definición sufre una dilatación extrema en el tiempo. El tiempo transcurrido en el reloj es muy pequeño. A medida que\(\epsilon\) se acerca a cero, y la relación entre A y B se acerca a una ligera, este tiempo de reloj se acerca a cero. En este sentido, la noción relativista de “distancia” es muy distinta de la euclídea. En geometría euclidiana, la distancia entre dos puntos sólo puede ser cero si son el mismo punto.

La división de casos involucrada en la definición relativista es un poco fea. Habiendo elaborado la interpretación física, ahora podemos consolidar la definición de una manera más agradable apelando a las coordenadas cartesianas.

Definición cartesiana de distancia en geometría euclidiana

Dado un vector\((\Delta x,\Delta y)\) del punto A al punto B, el cuadrado de la distancia entre ellos se define como\(\overline{\text{AB}}^2=\Delta x^2+\Delta y^2\).

Definición del intervalo en la relatividad

Dados puntos separados por diferencias de coordenadas\(\Delta x\)\(\Delta y\),\(\Delta z\), y\(\Delta t\), el intervalo espacio-tiempo\(\mathcal I\) (letra cursiva “I”) entre ellos se define como\(\mathcal I = \Delta t^2-\Delta x^2-\Delta y^2-\Delta z^2\).

Esto se expresa en unidades naturales, por lo que los cuatro términos del lado derecho tienen las mismas unidades; en unidades métricas con\(c \ne 1\),\(c\) deben insertarse factores apropiados de para que las unidades de los términos acuerden. El intervalo\(\mathcal I\) es positivo si AB es similar al tiempo (independientemente de qué evento viene primero), cero si es similar a la luz y negativo si es espacial. Ya que\(\mathcal I\) puede ser negativo, en general no podemos tomar su raíz cuadrada y definir un número real\(\overline{\text{AB}}\) como en el caso euclidiano. Cuando el intervalo es parecido al tiempo, podemos interpretar\(\sqrt{\mathcal I}\) como un tiempo, y cuando es espacial podemos tomar\(\sqrt{-\mathcal I}\) para ser una distancia.

La definición euclidiana de distancia (es decir, el teorema de Pitágoras) es útil porque da la misma respuesta independientemente de cómo rotemos el plano. Si bien se afirma en términos de cierto sistema de coordenadas, su resultado se define de manera inequívoca porque es el mismo independientemente del sistema de coordenadas que escojamos arbitrariamente. De igual manera,\(\mathcal I\) es útil porque, como se demuestra en el ejemplo 8 a continuación, es lo mismo independientemente de nuestro marco de referencia, es decir, independientemente de nuestra elección de coordenadas.

Ejemplo\(\PageIndex{7}\): Pioneer 10

\(\triangleright\)La sonda espacial Pioneer 10 se lanzó en 1972, y en 1973 fue la primera nave en volar por el planeta Júpiter. Cruzó la órbita del planeta Neptuno en 1983, tras lo cual se recibieron datos de telemetría hasta 2002. El siguiente cuadro da la posición de la nave espacial con respecto al sol exactamente a la medianoche del 1 de enero de 1983 y el 1 de enero de 1995. Se toma para ser la fecha de 1983\(t=0\).

t (s)	x	y	z
0	1.784 X 10 ^12 m	3.951 X 10 ^12 m	0.237 X 10 ^12 m
3.7869120000 X 10 ^8 s	2.420 X 10 ^12 m	8.827 X 10 ^12 m	0.488 X 10 ^12 m

Compara el tiempo transcurrido en la nave espacial con el tiempo en un marco de referencia atado al sol.

\(\triangleright\)Podemos convertir estos datos en unidades naturales, siendo la unidad de distancia la segunda (es decir, una luz-segundo, la distancia que la luz recorre en un segundo) y siendo la unidad de tiempo segundos. Convirtiendo y llevando a cabo esta resta, tenemos:

Δ t (s)	Δ x	Δ y	Δ z
3.7869120000 X 10 ^8 s	0.212 X 10 ^4 s	1.626 X 10 ^4 s	0.084 X 10 ^4 s

Comparando los exponentes de los números temporales y espaciales, podemos ver que la nave espacial se movía a una velocidad del orden de la velocidad\(10^{-4}\) de la luz, por lo que los efectos relativistas deberían ser pequeños pero no completamente despreciables.

Dado que el intervalo es parecido al tiempo, podemos tomar su raíz cuadrada e interpretarla como el tiempo transcurrido en la nave espacial. El resultado es\(\sqrt{\mathcal I}=3.786911996\times 10^8\ \text{s}\). Esto es 0.4 s menos que el tiempo transcurrido en el marco de referencia del sol.

z/Rectángulos de luz, ejemplo 8.
1. El rectángulo de luz gris representa el conjunto de todos los eventos como P que podrían visitarse después de A y antes de B.
2. El rectángulo se convierte en un cuadrado en el marco en el que A y B ocurren en la misma ubicación en el espacio.
3. El área del cuadrado discontinuo es\(\tau^2\), por lo que el área del cuadrado gris es\(\tau^2/2\).

Ejemplo\(\PageIndex{8}\): Invariance of the interval

En este ejemplo demostramos que el intervalo es el mismo independientemente de en qué marco de referencia lo calculemos. Esto se llama “invarianza de Lorentz”. La prueba se limita al caso temporal. Dados los eventos A y B, construya el rectángulo de luz como se define en la figura ab /1. En la p. 389 probamos que la transformación de Lorentz no cambia el área de una forma en el\(t\) plano\(x\) -. Por lo tanto, el área de este rectángulo no cambia si cambiamos al marco de referencia ab /2, en el que A y B ocurrieron en la misma ubicación y estaban separados por un intervalo de tiempo\(\tau\). Esta área equivale a la mitad del intervalo\(\mathcal I\) entre A y B. Pero un cálculo sencillo muestra que el rectángulo en ab /1 también tiene un área igual a la mitad del intervalo calculado en ese fotograma. Dado que el área en cualquier fotograma es igual a la mitad del intervalo, y el área es la misma en todos los fotogramas, el intervalo también es igual en todos los fotogramas.

ab/Ejemplo 8.

Ejemplo\(\PageIndex{9}\): A numerical example of invariance

ac/Ejemplo 9.

La figura ac muestra dos marcos de referencia en movimiento uno con respecto al otro en\(v=3/5\). (Para esta velocidad, el estiramiento y el estrujado de las diagonales principales son ambos por un factor de 2.) Los eventos se marcan en coordenadas que en el marco representado por el cuadrado son

\[\begin{align*} (t,x) & = (0,0) \text{and} \\ (t,x) &= (13,11) . \end{align*}\]

El intervalo entre estos eventos es\(13^2-11^2=48\). En el marco representado por el paralelogramo, los mismos dos eventos se encuentran en las coordenadas

\[\begin{align*} (t',x') & = (0,0) \text{and} \\ (t',x') &= (8,4) . \end{align*}\]

Calculando el intervalo usando estos valores, el resultado es
\(8^2-4^2=48\), que sale igual que en el otro fotograma.

Cuatro vectores y el producto interno

El Ejemplo 7 hace natural que definamos un tipo de vector con cuatro componentes, el primero relativo al tiempo y los otros espaciales. Estos se conocen como cuatro vectores. Está claro cómo debemos definir el equivalente de un producto punto en la relatividad:

\[\begin{equation*} \mathbf{A}\cdot\mathbf{B} = A_t B_t - A_xB_x - A_yB_y - A_zB_z \end{equation*}\]

El término “producto punto” tiene connotaciones de referirse solo a tres vectores, por lo que la operación de tomar el producto escalar de dos cuatro vectores generalmente se denomina en su lugar como el “producto interno”. El intervalo espacio-tiempo puede entonces ser considerado como el producto interno de un cuatro vector consigo mismo. Nos importa el producto interno relativista exactamente por la misma razón que nos importa su versión euclidiana; ambos son escalares, por lo que tienen un valor fijo independientemente del sistema de coordenadas que escojamos.

Ejemplo 10: La paradoja de los gemelos

Alice y Betty son gemelas idénticas. Betty realiza un viaje espacial a velocidades relativistas, viajando lejos de la tierra para luego darse la vuelta y regresar. En tanto, Alice se queda en la tierra. Cuando Betty regresa, es más joven que Alice debido a la dilatación relativista del tiempo (ejemplo 1, p. 391). Pero, ¿no es válido decir que la nave espacial de Betty está quieta y la tierra se mueve? En esa descripción, ¿Alice no terminaría siendo más joven y Betty mayor? A esto se le conoce como la “paradoja gemela”. Realmente no puede ser una paradoja, ya que es exactamente lo que se observó en el experimento de Hafele-Keating (p. 381). La pista de Betty en el\(t\) plano\(x\) - (su “línea mundial” en jerga relativista) consiste en vectores\(\mathbf{b}\) y\(\mathbf{c}\) encadenados de extremo a extremo (figura ad). Podríamos adoptar un marco de referencia en el que Betty estuvo en reposo durante\(\mathbf{b}\) (es decir,\(b_x=0\)), pero no hay marco en el que\(\mathbf{b}\) y\(\mathbf{c}\) son paralelos, por lo que no hay marco en el que Betty estuvo en reposo durante ambos\(\mathbf{b}\) y\(\mathbf{c}\). Esto resuelve la paradoja. Ya hemos establecido por otros métodos que Betty envejece menos que Alice, pero veamos cómo se desarrolla esto en un simple ejemplo numérico. Omitiendo unidades e inventando números simples, digamos que los vectores en el anuncio de figura son \[\begin{align*} \mathbf{a} &= (6,1) \\ \mathbf{b} &= (3,2) \\ \mathbf{c} &= (3,-1) , \end{align*}\] donde los componentes se dan en el orden\((t,x)\). El tiempo que vive Alice es entonces \[\begin{equation*} |\mathbf{a}| = \sqrt{6^2-1^2} =5.9 , \end{equation*}\] que es mayor que el tiempo transcurrido de Betty \[\begin{equation*} |\mathbf{b}|+|\mathbf{c}| = \sqrt{3^2-2^2}+\sqrt{3^2-(-1)^2} = 5.1 . \end{equation*}\]

Ejemplo 11: Simultaneidad usando productos internos

ac/Ejemplo 11. Supongamos que un observador O se mueve inercialmente a lo largo de un vector\(\mathbf{o}\), y deja que el vector que separa dos eventos P y Q sea\(\mathbf{s}\). O juzga que estos eventos sean simultáneos si\(\mathbf{o}\cdot\mathbf{s}=0\). Para ver por qué esto es cierto, supongamos que elegimos un sistema de coordenadas como lo define O. En este sistema de coordenadas, O se considera que está en reposo, por lo que dice que su vector tiene sólo un componente de tiempo,\(\mathbf{o}=(\Delta t,0,0,0)\). Si considera que P y Q son simultáneos, entonces el vector de P a Q es de la forma\((0,\Delta x,\Delta y,\Delta z)\). El producto interno es entonces cero, ya que cada uno de los cuatro términos desaparece. Dado que el producto interno es independiente de la elección del sistema de coordenadas, no importa que elegimos uno atado a O misma. Cualquier otro observador\(\text{O}'\) puede mirar la moción de O, notarlo\(\mathbf{o}\cdot\mathbf{s}=0\), e inferir que O debe considerar P y Q como simultáneos, aunque\(\text{O}'\) diga que no lo fueron.

Desplazamientos Doppler de luz y adición de velocidades

Cuando los desplazamientos Doppler ocurren con ondas en un estanque o las ondas sonoras de un avión, pueden depender del movimiento relativo de tres objetos diferentes: la fuente, el receptor y el medio. Pero las ondas de luz no tienen un medio. Por lo tanto, los desplazamientos Doppler de luz solo pueden depender del movimiento relativo de la fuente y el observador.

ad/El patrón de olas hecho por una fuente puntual que se mueve hacia la derecha a través del agua. Tenga en cuenta la longitud de onda más corta de las ondas emitidas hacia adelante y la longitud de onda más larga de las ondas hacia atrás.

Un caso sencillo es aquel en el que el movimiento relativo de la fuente y el receptor es perpendicular a la línea que los conecta. Es decir, el movimiento es transversal. Los desplazamientos Doppler no relativistas ocurren porque la distancia entre la fuente y el receptor está cambiando, por lo que en la física no relativista no esperamos ningún cambio Doppler en absoluto cuando el movimiento es transversal, y esto es lo que de hecho se observa con alta precisión. Por ejemplo, la foto muestra longitudes de onda acortadas y alargadas a la derecha e izquierda, a lo largo de la línea de movimiento de la fuente, pero un observador por encima o por debajo de la fuente mide solo la longitud de onda y frecuencia normales, no desplazadas. Pero relativisticamente, tenemos un efecto de dilatación temporal, por lo que para las ondas de luz emitidas transversalmente, hay un desplazamiento Doppler de\(1/\gamma\) frecuencia (o\(\gamma\) en longitud de onda).

El otro caso sencillo es aquel en el que el movimiento relativo de la fuente y el receptor es longitudinal, es decir, se acercan o retroceden el uno del otro. Por ejemplo, las galaxias distantes están retrocediendo de nuestra galaxia debido a la expansión del universo, y esta expansión se detectó originalmente porque se observaron desplazamientos Doppler hacia el extremo rojo (baja frecuencia) del espectro.

De manera no relativista, esperaríamos que la luz de tal galaxia fuera Doppler desplazada hacia abajo en frecuencia por algún factor, lo que dependería de las velocidades relativas de tres objetos diferentes: la fuente, el medio de la onda y el receptor. Relativisticamente, las cosas se vuelven más simples, porque la luz no es una vibración de un medio físico, por lo que el desplazamiento Doppler sólo puede depender de una sola velocidad\(v\), que es la velocidad a la que aumenta la separación entre la fuente y el receptor.

ae/Una representación gráfica de la transformación de Lorentz para una velocidad de\((3/5)c\). La diagonal larga se estira por un factor de dos, la corta tiene la mitad de su longitud anterior, y el área es la misma que antes.

af/En el evento O, la fuente y el receptor están uno encima del otro, así como la fuente emite una cresta de onda, se recibe sin ningún retraso de tiempo. En P, la fuente emite otra cresta de onda, y en Q el receptor la recibe.

El cuadrado en la figura af es el “papel cuadriculado” utilizado por alguien que considera que la fuente está en reposo, mientras que el paralelogramo juega un papel similar para el receptor. La figura se dibuja para el caso donde\(v=3/5\) (en unidades donde\(c=1\)), y en este caso el factor de estiramiento de la diagonal larga es 2. Para mantener el área igual, la diagonal corta tiene que ser comprimida a la mitad de su tamaño original. Pero ahora es cuestión de geometría simple mostrar que OP equivale a la mitad del ancho del cuadrado, y esto nos dice que el desplazamiento Doppler es un factor de 1/2 en frecuencia. Es decir, el factor squish de la diagonal corta se interpreta como el desplazamiento Doppler. Para obtener esto como una ecuación general para velocidades distintas a 3/5, se puede demostrar al tocar el violín directo con el resultado de la parte c del problema 7 en la p. 439 que el desplazamiento Doppler es

\[\begin{equation*} D(v) = \sqrt{\frac{1-v}{1+v}} . \end{equation*}\]

Aquí\(v>0\) está el caso donde la fuente y el receptor se están separando más,\(v\lt0\) el caso en el que se acercan. (Esto es lo opuesto a la convención de signos utilizada en la subsección 6.1.5. Es conveniente cambiar las convenciones aquí para que podamos usar valores positivos de\(v\) en el caso de los desplazamientos cosmológicos al rojo, que son la aplicación más importante.)

Supongamos que Alice se queda en casa en la tierra mientras su gemela Betty despega en su cohete a 3/5 de la velocidad de la luz. Cuando aprendí por primera vez la relatividad, lo que más dolor me causó fue entender cómo cada observador podía decir que el otro era aquel cuyo tiempo era lento. Me pareció que si pudiera tomar una pastilla que acelerara mi mente y mi cuerpo, entonces naturalmente vería a todos los demás como lentos. ¿No debería aplicarse lo mismo a la relatividad? Pero supongamos que Alice y Betty se ponen en la radio y tratan de resolver quién es el rápido y quién es el lento. La voz de cada gemelo suena enloquecido doooowwwwn al otro. Si Alice aplaude dos veces, en un intervalo de tiempo de un segundo por su reloj, Betty escucha los aplausos que vienen por radio con dos segundos de diferencia, pero la situación es exactamente simétrica, y Alice escucha lo mismo si Betty aplaude. Cada gemelo analiza la situación utilizando un diagrama idéntico a ah, y atribuye las observaciones de su hermana a una complicada combinación de distorsión del tiempo, el tiempo que tardan las señales de radio en propagarse y el movimiento de su gemelo relativo a ella.

autocomprobación:

Dale la vuelta a tu libro y reinterpreta la figura ah.

(respuesta en la parte posterior de la versión PDF del libro)

Ejemplo 12: Una propiedad de simetría del efecto Doppler
Supongamos que A y B están en reposo uno respecto al otro, pero C se mueve a lo largo de la línea entre A y B. A transmite una señal a C, quien luego la retransmite a B. La señal acumula dos desplazamientos Doppler, y el resultado es su producto\(D(v)D(-v)\). Pero este producto debe ser igual a 1, así que debemos tener\(D(-v)D(v)=1\), que se puede verificar directamente a partir de la ecuación.

Ejemplo 13: El experimento Ives-Stilwell

El resultado del ejemplo 12 fue la base de una de las primeras pruebas de laboratorio de relatividad especial, realizadas por Ives y Stilwell en 1938. Observaron la luz emitida por excitado por un haz de\(\text{H}_2^+\) e\(\text{H}_3^+\) iones con velocidades de unas décimas de por ciento de\(c\). Al medir la luz tanto por delante como por detrás de los haces, encontraron que el producto de los desplazamientos Doppler\(D(v)D(-v)\) era igual a 1, según lo predicho por la relatividad. Si la relatividad hubiera sido falsa, entonces uno habría esperado que el producto difiriera de 1 por una cantidad que habría sido detectable en su experimento. En 2003, Saathoff et al. llevaron a cabo una versión extremadamente precisa de la técnica Ives-Stilwell con\(\text{Li}^+\) iones moviéndose a 6.4% de\(c\). Las frecuencias observadas, en unidades de MHz, fueron: f o = 546466918.8±0.4 (frecuencia no desplazada) f o D (-v) = 582490203.44±.09 (frecuencia desplazada, adelante) f o D (v) = 512671442.9±0.5 (frecuencia desplazada, hacia atrás) \(\sqrt{f_\text{o}D(-v)\cdot f_\text{o} D(v)}\) =546466918.6±0.3 Los resultados muestran un acuerdo increíblemente preciso entre\(f_\text{o}\) y\(\sqrt{f_\text{o}D(-v)\cdot f_\text{o} D(v)}\), como se esperaba relativisticamente porque\(D(v)D(-v)\) se supone que es igual a 1. El acuerdo se extiende a 9 cifras significativas, mientras que si la relatividad hubiera sido falsa debería haber habido un desacuerdo relativo de aproximadamente\(v^2=.004\), es decir, una discrepancia en la tercera cifra significativa. El espectacular acuerdo con la teoría ha hecho de este experimento un pararrayos para los chiflados antirelatividad.

Vimos en la p. 394 que no debe esperarse que las velocidades relativistas sean exactamente aditivas, y el problema 1 en la p. 438 lo verifica en el caso especial donde A se mueve con relación a B at\(0.6c\) y B con relación a C at\(0.6c\) — el resultado no siendo\(1.2c\). El desplazamiento Doppler relativista proporciona una manera sencilla de derivar una ecuación general para la combinación relativista de velocidades; el problema 17 en la p. 442 le guía a través de los pasos de esta derivación, y el resultado se da en la p. 936.

Colaboradores y Atribuciones

• Template:ContribCrowell