10.2: Circuitos paralelos y en serie

En la sección 9.1, nos limitamos a circuitos relativamente simples, esencialmente nada más que una batería y una sola bombilla. El propósito de este capítulo es presentarle circuitos más complejos, que contienen múltiples resistencias o fuentes de voltaje en serie, en paralelo, o ambas.

9.2.1 Esquemas

Veo una posición de ajedrez; Kasparov ve una interesante variación de Ruy López. Para los no iniciados, un esquema puede parecer tan ininteligible como los jeroglíficos mayas, pero incluso un poco de entrenamiento ocular puede recorrer un largo camino para hacer que su significado salte de la página. Un esquema es un dibujo estilizado y simplificado de un circuito. El propósito es eliminar tantas características irrelevantes como sea posible, para que las relevantes sean más fáciles de elegir.

a/1. Mal: Las formas de los cables son irrelevantes. 2. Incorrecto: Deben usarse ángulos rectos. 3. Mal: Se hace un patrón simple para parecer desconocido y complicado. 4. Derecha.

Un ejemplo de una característica irrelevante es la forma física, la longitud y el diámetro de un cable. En casi todos los circuitos, es una buena aproximación asumir que los cables son conductores perfectos, de modo que cualquier pieza de cable ininterrumpida por otros componentes tenga voltaje constante en todo el mismo. Cambiar la longitud del cable, por ejemplo, no cambia este hecho. (Por supuesto, si usáramos millas y millas de cable, como en una línea telefónica, la resistencia del cable comenzaría a sumar, y su longitud comenzaría a importar). Las formas de los alambres son igualmente irrelevantes, por lo que los dibujamos con formas estandarizadas y estilizadas hechas solo de líneas verticales y horizontales con curvas de ángulo recto en ellas. Esto tiene el efecto de hacer que circuitos similares se parezcan más y nos ayuden a reconocer patrones familiares, así como las palabras en un periódico son más fáciles de reconocer que las escritas a mano. En la figura a se muestran algunos ejemplos de estos conceptos.

b/Las dos áreas sombreadas con forma de letra “E” son ambas regiones de voltaje constante.

El primer paso más importante para aprender a leer esquemas es aprender a reconocer piezas contiguas de alambre que deben tener voltaje constante en todas partes. En la figura b, por ejemplo, las dos piezas de alambre sombreadas en forma de E deben tener cada una tensión constante. Esto enfoca nuestra atención en dos de las principales incógnitas que nos gustaría poder predecir: la tensión de la E izquierda y la tensión de la de la derecha.

9.2.2 Resistencias paralelas y regla de unión

Uno de los ejemplos más simples de analizar es el circuito de resistencia paralelo, del cual la figura b fue un ejemplo. En general podemos tener resistencias desiguales\(R_1\) y\(R_2\), como en c/1. Dado que solo hay dos áreas de voltaje constante en el circuito, c /2, los tres componentes tienen la misma diferencia de voltaje a través de ellos. Una batería normalmente logra mantener las diferencias de voltaje a través de sí misma para las que fue diseñada, por lo que las caídas de voltaje\(\Delta V_1\) y\(\Delta V_2\) a través de las resistencias deben ser iguales al voltaje de la batería:

\[\begin{equation*} \Delta V_1=\Delta V_2=\Delta V_{battery} . \end{equation*}\]

Cada resistencia siente así la misma diferencia de voltaje que si fuera la única en el circuito, y la ley de Ohm nos dice que la cantidad de corriente que fluye a través de cada una es también la misma que habría sido en un circuito de una resistencia. Es por ello que los circuitos eléctricos domésticos están cableados en paralelo. Queremos que todos los electrodomésticos funcionen igual, independientemente de si otros aparatos están enchufados o desenchufados, encendidos o apagados. (La compañía eléctrica no usa baterías por supuesto, pero nuestro análisis sería el mismo para cualquier dispositivo que mantenga un voltaje constante).

c/1. Dos resistencias en paralelo. 2. Hay dos áreas de voltaje constante. 3. La corriente que sale de la batería se divide entre las dos resistencias, y posteriormente se reúne. 4. Las dos resistencias en paralelo se pueden tratar como una sola resistencia con un valor de resistencia menor.

Por supuesto que la compañía eléctrica puede decir cuándo encendemos cada luz de la casa. ¿Cómo lo saben? La respuesta es que dibujamos más actuales. Cada resistencia atrae una cierta cantidad de corriente, y la cantidad que se tiene que suministrar es la suma de las dos corrientes individuales. La corriente es como un río que se divide por la mitad, c/3, y luego se reúne. La corriente total es

\[\begin{equation*} I_{total} = I_1 + I_2 . \end{equation*}\]

Este es un ejemplo de un hecho general llamado regla de cruce:

En cualquier circuito que no esté almacenando o liberando carga, la conservación de la carga implica que la corriente total que fluye fuera de cualquier unión debe ser la misma que la corriente total que fluye adentro.

Volviendo al análisis de nuestro circuito, aplicamos la ley de Ohm a cada resistencia, resultando en

\[\begin{align*} I_{total} &= \Delta V/R_1+ \Delta V/R_2 \\ &= \Delta V\left(\frac{1}{R_1}+\frac{1}{R_2}\right) . \end{align*}\]

En lo que respecta a la compañía eléctrica, toda su casa es solo una resistencia con alguna resistencia\(R\), llamada la resistencia equivalente. Escribirían la ley de Ohm como

\[\begin{equation*} I_{total} = \Delta V/R , \end{equation*}\]

a partir de la cual podemos determinar la resistencia equivalente en comparación con la expresión anterior:

\[\begin{align*} 1/R &= \frac{1}{R_1}+\frac{1}{R_2} \\ R &= \left(\frac{1}{R_1}+\frac{1}{R_2}\right)^{-1} \end{align*}\]

[resistencia equivalente de dos resistencias en paralelo]

Dos resistencias en paralelo, c/4, son equivalentes a una sola resistencia con un valor dado por la ecuación anterior.

Ejemplo 10: Dos lámparas en el mismo circuito doméstico

\(\triangleright\)Enciendes dos lámparas que están en el mismo circuito doméstico. Cada uno tiene una resistencia de 1 ohm. ¿Cuál es la resistencia equivalente y cómo se compara la disipación de potencia con el caso de una sola lámpara? \(\triangleright\)La resistencia equivalente de las dos lámparas en paralelo es \[\begin{align*} R &= \left(\frac{1}{ R_1}+\frac{1}{ R_2}\right)^{-1} \\ &= \left(\frac{1}{1\ \Omega}+\frac{1}{1\ \Omega}\right)^{-1} \\ &= \left(1\ \Omega^{-1} + 1\ \Omega^{-1}\right)^{-1} \\ &= \left(2\ \Omega^{-1}\right)^{-1} \\ &= \text{0.5}\ \Omega \end{align*}\] La diferencia de voltaje en todo el circuito es siempre los 110 V establecidos por la compañía eléctrica (es corriente alterna, pero eso es irrelevante). La resistencia de todo el circuito se ha cortado a la mitad al encender la segunda lámpara, por lo que una cantidad fija de voltaje producirá el doble de corriente. Dos veces la corriente que fluye a través de la misma diferencia de voltaje significa el doble de disipación de energía, lo cual tiene sentido.

El corte a la mitad de la resistencia sorprende a muchos estudiantes, ya que estamos “sumando más resistencia” al circuito al poner en la segunda lámpara. ¿Por qué la resistencia equivalente resulta ser menor que la resistencia de una sola lámpara? Este es un caso donde el razonamiento puramente verbal puede ser engañoso. Un elemento de circuito resistivo, como el filamento de una bombilla, no es ni un aislante perfecto ni un conductor perfecto. En lugar de analizar este tipo de circuitos en términos de “resistencias”, es decir, aisladores parciales, podríamos haber hablado de “conductores”. Este ejemplo parecería entonces razonable, ya que “agregamos más conductancia”, pero entonces uno tendría la expectativa incorrecta sobre el caso de las resistencias en serie, discutida en la siguiente sección.

Quizás una forma más productiva de pensarlo es usar la intuición mecánica. Por analogía, tus fosas nasales resisten el flujo de aire a través de ellas, pero tener dos fosas nasales hace que sea dos veces más fácil respirar.

Ejemplo 11: Tres resistencias en paralelo

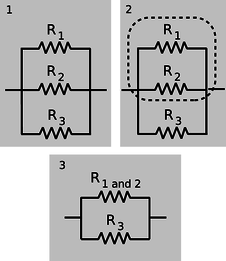
\(\triangleright\)¿Qué pasa si tenemos tres o más resistencias en paralelo? d/Tres resistencias en paralelo. \(\triangleright\)Este es un ejemplo importante, porque la solución implica una técnica importante para entender los circuitos: descomponerlos en partes más pequeñas y simplificarlos. En el circuito d /1, con tres resistencias en paralelo, podemos pensar en dos de las resistencias como formando una sola resistencia grande, d /2, con resistencia equivalente \[\begin{equation*} R_{12} = \left(\frac{1}{ R_1}+\frac{1}{ R_2}\right)^{-1} . \end{equation*}\] Entonces podemos simplificar el circuito como se muestra en d /3, de manera que contenga sólo dos resistencias. La resistencia equivalente de todo el circuito viene dada por \[\begin{equation*} R_{123} = \left(\frac{1}{ R_{12}}+\frac{1}{ R_3}\right)^{-1} . \end{equation*}\] Sustituyendo\(R_{12}\) y simplificando, encontramos el resultado \[\begin{equation*} R_{123} = \left(\frac{1}{ R_1}+\frac{1}{ R_2}+\frac{1}{ R_3}\right)^{-1} , \end{equation*}\] que probablemente podrías haber adivinado. El punto interesante aquí es el concepto de dividir y conquistar, no el resultado matemático.

Ejemplo 12: Un número arbitrario de resistencias idénticas en paralelo

\(\triangleright\)¿Cuál es la resistencia de resistencias\(N\) idénticas en paralelo? \(\triangleright\)Generalizando los resultados para dos y tres resistencias, tenemos \[\begin{equation*} R_{N} = \left(\frac{1}{ R_1}+\frac{1}{ R_2}+...\right)^{-1} , \end{equation*}\] donde “...” significa que la suma incluye todas las resistencias. Si todas las resistencias son idénticas, esto se convierte \[\begin{align*} R_{N} &= \left(\frac{ N}{ R}\right)^{-1} \\ &= \frac{ R}{ N} \end{align*}\]

Ejemplo 13: Dependencia de la resistencia en el área de la sección transversal

e/Unir cuatro resistencias en paralelo equivale a hacer una sola resistencia con la misma longitud pero cuatro veces el área de la sección transversal. El resultado es hacer una resistencia con una cuarta parte de la resistencia. Hemos aludido brevemente al hecho de que la resistencia eléctrica de un objeto depende de su tamaño y forma, pero ahora estamos listos para comenzar a hacer más declaraciones matemáticas al respecto. Como sugiere la figura e, aumentar el área de la sección transversal de una resistencia equivale a agregar más resistencias en paralelo, lo que conducirá a una disminución general de la resistencia. Cualquier resistencia real con lados rectos y paralelos se puede cortar en una gran cantidad de piezas, cada una con un área de sección transversal de, digamos, 1\(\mu \text{m}^2\). El número,\(N\), de tales cortes es proporcional al área total de la sección transversal de la resistencia, y por aplicación del resultado del ejemplo anterior, por lo tanto encontramos que la resistencia de un objeto es inversamente proporcional a su área de sección transversal. f/Una pipa gorda tiene menos resistencia que una pipa flaca. Se mantiene una relación análoga para las tuberías de agua, razón por la cual las líneas troncales de alto flujo tienen que tener grandes áreas de sección transversal. Para hacer que mucha agua (corriente) fluya a través de una tubería delgada, necesitaríamos una diferencia de presión (voltaje) impracticamente grande.

Ejemplo 14: Lecturas incorrectas de un voltímetro

g/Un voltímetro es realmente un amperímetro con una resistencia interna. Cuando medimos la diferencia de voltaje a través de una resistencia, 1, realmente estamos construyendo un circuito de resistencia paralelo, 2. Un voltímetro es realmente solo un amperímetro con una resistencia interna, y usamos un voltímetro en paralelo con lo que estamos tratando de medir la diferencia de voltaje a través. Esto significa que cada vez que medimos la caída de voltaje a través de una resistencia, esencialmente estamos poniendo dos resistencias en paralelo. El amperímetro dentro del voltímetro puede ser ignorado con el propósito de analizar cómo fluye la corriente en el circuito, ya que es esencialmente solo un cable enrollado con una resistencia muy baja. Ahora bien, si estamos realizando esta medición en una resistencia que forma parte de un circuito más grande, hemos cambiado el comportamiento del circuito a través de nuestro acto de medir. Es como si hubiéramos modificado el circuito reemplazando la resistencia\(R\) por la resistencia equivalente más pequeña de\(R\) y\(R_v\) en paralelo. Es por esta razón que los voltímetros se construyen con la mayor resistencia interna posible. Como ejemplo numérico, si usamos un voltímetro con una resistencia interna de 1\(M\Omega \) para medir la caída de voltaje a través de una resistencia de un ohmio, la resistencia equivalente es 0.999999\(\Omega \), que no es lo suficientemente diferente como para hacer ninguna diferencia. Pero si intentáramos usar el mismo voltímetro para medir la caída de voltaje a través de una\(2-M\Omega \) resistencia, estaríamos reduciendo la resistencia de esa parte del circuito en un factor de tres, lo que produciría un cambio drástico en el comportamiento de todo el circuito.

Esta es la razón por la que no se puede utilizar un voltímetro para medir la diferencia de voltaje entre dos puntos diferentes en el aire, o entre los extremos de una pieza de madera. Esto de ninguna manera es una estupidez querer hacer, ya que el mundo que nos rodea no es un entorno de voltaje constante, siendo el ejemplo más extremo cuando se está gestando una tormenta eléctrica. Pero no funcionará con un voltímetro ordinario porque la resistencia del aire o la madera es de muchos gigaohmios. El efecto de ondear un par de sondas de voltímetro alrededor en el aire es que proporcionamos una ruta de reunificación para las cargas positivas y negativas que se han separado, a través del propio voltímetro, que es un buen conductor en comparación con el aire. Esto reduce a cero la diferencia de voltaje que estábamos tratando de medir.

En general, se dice que un voltímetro que se ha configurado con un circuito abierto (o una resistencia muy grande) entre sus sondas es “flotante”. Un voltímetro analógico anticuado del tipo descrito aquí leerá cero cuando se deje flotando, lo mismo que cuando estaba sentado en la repisa. Un voltímetro digital flotante suele mostrar un mensaje de error.

9.2.3 Resistencias de la serie

h/1. Una batería impulsa la corriente a través de dos resistencias en serie. 2. Hay tres regiones de voltaje constante. 3. Las tres diferencias de voltaje están relacionadas. 4. Si el medidor cangrejo camina alrededor del circuito sin voltear o cruzar sus patas, los voltajes resultantes tienen signos más y menos que los hacen sumar a cero.

Los dos diseños básicos de circuitos son paralelos y en serie, por lo que un par de resistencias en serie, h /1, es otro de los circuitos más básicos que podemos hacer. Por conservación de carga, toda la corriente que fluye a través de una resistencia también debe fluir a través de la otra (así como a través de la batería):

\[\begin{equation*} I_1 = I_2 . \end{equation*}\]

La única forma en que la información sobre los dos valores de resistencia va a ser útil es si podemos aplicar la ley de Ohm, que relacionará la resistencia de cada resistor con la corriente que fluye a través de ella y la diferencia de voltaje a través de ella. La figura h /2 muestra las tres áreas de voltaje constante. Las diferencias de voltaje son más significativas físicamente que las tensiones, por lo que definimos símbolos para las diferencias de voltaje a través de las dos resistencias en la figura h /3.

Contamos con tres áreas de voltaje constante, con símbolos para la diferencia de voltaje entre cada par posible de ellas. Estas tres diferencias de voltaje deben estar relacionadas entre sí. Es como si te dijera que Fred es un pie más alto que Ginger, Ginger es un pie más alto que Sally, y Fred es dos pies más alto que Sally. La información es redundante, y realmente solo necesitabas dos de los tres datos para inferir el tercero. En el caso de nuestras diferencias de voltaje, tenemos

\[\begin{equation*} |\Delta V_1| + |\Delta V_2| = |\Delta V_{battery}| . \end{equation*}\]

Los signos de valor absoluto se deben a la ambigüedad en cómo definimos nuestras diferencias de voltaje. Si invertiéramos las dos sondas del voltímetro, obtendríamos un resultado con el signo contrario. Los voltímetros digitales en realidad proporcionarán un signo menos en la pantalla si el cable conectado al enchufe “V” tiene un voltaje más bajo que el conectado al enchufe “COM”. Los voltímetros analógicos fijan la aguja contra una clavija si intentas usarlos para medir voltajes negativos, por lo que tienes que jugar para que los cables se conecten de la manera correcta, y luego suministrar cualquier signo menos necesario usted mismo.

La Figura h/4 muestra una forma estándar de cuidar la ambigüedad en los signos. Para cada una de las tres mediciones de voltaje alrededor del bucle, mantenemos la misma sonda (la más oscura) en el lado de las agujas del reloj. Es como si el voltímetro estuviera vagando por el circuito como un cangrejo, sin nunca “cruzar las patas”. Con esta convención, la relación entre las caídas de voltaje se convierte

\[\begin{equation*} \Delta V_1 + \Delta V_2 = -\Delta V_{battery} , \end{equation*}\]

o, en forma más simétrica,

\[\begin{equation*} \Delta V_1 + \Delta V_2 + \Delta V_{battery} = 0 . \end{equation*}\]

De manera más general, esto se conoce como la regla de bucle para analizar circuitos:

Asumiendo la convención estándar para los signos más y menos, la suma de las caídas de voltaje alrededor de cualquier bucle cerrado en un circuito debe ser cero.

Buscar una excepción a la regla del bucle sería como pedir una caminata que sería cuesta abajo hasta el final y ¡que volvería a su punto de partida!

Para el circuito que nos propusimos analizar, la ecuación

\[\begin{equation*} \Delta V_1 + \Delta V_2 + \Delta V_{battery} = 0 \end{equation*}\]

ahora se puede reescribir aplicando la ley de Ohm a cada resistencia:

\[\begin{equation*} I_1R_1 + I_2R_2 + \Delta V_{battery} = 0 . \end{equation*}\]

Las corrientes son las mismas, así podemos factorizarlas:

\[\begin{equation*} I\left(R_1 + R_2\right) + \Delta V_{battery} = 0 , \end{equation*}\]

y este es el mismo resultado que habríamos obtenido si hubiéramos estado analizando un circuito de una resistencia con resistencia\(R_1+R_2\). Así, la resistencia equivalente de las resistencias en serie equivale a la suma de sus resistencias.

Ejemplo 15: Dos bombillas en serie

\(\triangleright\)Si se colocan dos bombillas idénticas en serie, ¿cómo se comparan sus brillos con el brillo de una sola bombilla? i/Ejemplo 15. \(\triangleright\)Tomado en su conjunto, el par de bombillas actúan como una resistencia duplicada, por lo que extraerán la mitad de corriente de la pared. Cada bombilla será más tenue de lo que habría sido una sola bombilla. La potencia total disipada por el circuito es\(I\Delta V\). La caída de voltaje en todo el circuito es la misma que antes, pero la corriente se reduce a la mitad, por lo que el circuito de dos bombillas consume la mitad de energía total que el circuito de una bombilla. Cada bombilla consume una cuarta parte de la potencia normal. En términos generales, podríamos esperar que esto resulte en que una cuarta parte de la luz sea producida por cada bombilla, pero en realidad las bombillas desperdician un porcentaje bastante alto de su potencia en forma de calor y longitudes de onda de luz que no son visibles (infrarroja y ultravioleta). Se producirá menos luz, pero es difícil predecir exactamente cuánto menos, ya que la eficiencia de las bombillas se cambiará al operarlas bajo diferentes condiciones.

Ejemplo 16: Más de dos resistencias iguales en serie
Mediante la aplicación directa de la técnica de dividir y conquistar discutida en el apartado anterior, encontramos que la resistencia equivalente de resistencias\(N\) idénticas\(R\) en serie será\(NR\).

Ejemplo 17: Dependencia de la resistencia en la longitud

En la sección anterior, se demostró que la resistencia es inversamente proporcional al área de la sección transversal. Por razón equivalente sobre las resistencias en serie, encontramos que la resistencia es proporcional a la longitud. Análogamente, es más difícil soplar a través de una pajita larga que a través de una corta. j/Duplicar la longitud de una resistencia es como poner dos resistencias en serie. Se duplica la resistencia.

Armando los dos argumentos, encontramos que la resistencia de un objeto con lados rectos y paralelos viene dada por

\[\begin{equation*} R = \text{(constant)} \cdot L/ A \end{equation*}\]

A la constante de proporcionalidad se le llama resistividad, y sólo depende de la sustancia de la que esté hecho el objeto. Se podría utilizar una medición de resistividad, por ejemplo, para ayudar a identificar una muestra de una sustancia desconocida.

Ejemplo 18: Elección de alto voltaje para líneas eléctricas

Thomas Edison se involucró en una famosa controversia tecnológica sobre la diferencia de voltaje que debería usarse para las líneas de energía eléctrica. En este momento, el público no estaba familiarizado con la electricidad, y fácilmente se asustaba por ella. El presidente de Estados Unidos, por ejemplo, se negó a tener iluminación eléctrica en la Casa Blanca cuando se puso a disposición comercial por primera vez porque la consideró insegura, prefiriendo el conocido peligro de incendio de las lámparas de aceite a los misteriosos peligros de la electricidad. Principalmente como una forma de superar el miedo público, Edison creía que el poder debía transmitirse usando pequeños voltajes, y dio a conocer su opinión dando demostraciones en las que un perro fue atraído a su posición para ser asesinado por una gran diferencia de voltaje entre dos láminas de metal en el suelo. (Los oponentes de Edison también abogaron por la corriente alterna en lugar de la corriente continua, y la CA también es más peligrosa que la CC. Como discutiremos más adelante, la CA se puede aumentar y bajar fácilmente al nivel de voltaje deseado usando un dispositivo llamado transformador.) Ahora bien, si queremos entregar cierta cantidad de energía\(P_L\) a una carga como una bombilla eléctrica, solo estamos limitados por la ecuación\(P_{L} = I\Delta V_L\). Podemos entregar cualquier cantidad de energía que deseemos, incluso con un bajo voltaje, si estamos dispuestos a usar grandes corrientes. Las redes modernas de distribución eléctrica, sin embargo, utilizan diferencias peligrosamente altas de voltaje de decenas de miles de voltios. ¿Por qué perdió Edison el debate? Se reduce a dinero. La compañía eléctrica debe entregar la cantidad de energía\(P_L\) deseada por el cliente a través de una línea de transmisión cuya resistencia\(R_T\) está fijada por la economía y la geografía. La misma corriente fluye tanto a través de la carga como de la línea de transmisión, disipando la potencia útil en la primera y despilfarradamente en la segunda. La eficiencia del sistema es \[\begin{align*} \text{efficiency} &= \frac{\text{power paid for by the customer}} {\text{power paid for by the utility}} \\ &= \frac{ P_{L}}{ P_L+ P_{T}} \\ &= \frac{1}{1+ P_{T}/ P_L} \end{align*}\] Poniéndonos en la piel de la compañía eléctrica, deseamos deshacernos de la variable\(P_T\), ya que es algo que controlamos sólo indirectamente por nuestra elección de\(\Delta V_T\) y\(I\). Sustituyendo\(P_{T}= I\Delta V_T\), encontramos \[\begin{equation*} \text{efficiency} = \frac{1} {1+\frac{ I \Delta V_T}{ P_L}} \end{equation*}\] Suponemos que la línea de transmisión (pero no necesariamente la carga) es óhmica, por lo que la sustitución\(\Delta V_T=IR_T\) da \[\begin{equation*} efficiency = \frac{1}{1+\frac{I^2R_T}{P_L}} \end{equation*}\] Esta cantidad se puede maximizar claramente haciendo lo más pequeña\(I\) posible, ya que entonces estaremos dividiendo por la menor cantidad posible en la parte inferior de la fracción. Un circuito de baja corriente solo puede entregar cantidades significativas de energía si utiliza altos voltajes, razón por la cual los sistemas de transmisión eléctrica utilizan altos voltajes peligrosos.

Ejemplo 19: Ser asesinado por tu amperímetro

Al igual que con un voltímetro, un amperímetro puede dar lecturas erróneas si se usa de tal manera que cambie el comportamiento del circuito. Se usa un amperímetro en serie, por lo que si se usa para medir la corriente a través de una resistencia, el valor de la resistencia se cambiará efectivamente a\(R+ R_a\), donde\(R_a\) está la resistencia del amperímetro. Los amperímetros están diseñados con resistencias muy bajas para que sea poco\(R+ R_a\) probable que sean significativamente diferentes de\(R\). De hecho, el verdadero peligro es la muerte, ¡no una lectura equivocada! Prácticamente los únicos circuitos cuyas resistencias son significativamente menores que las de un amperímetro son los diseñados para transportar enormes corrientes. Un amperímetro insertado en dicho circuito puede fundirse fácilmente. Cuando trabajaba en un laboratorio financiado por el Departamento de Energía, recibimos boletines periódicos de la oficina de seguridad del DOE sobre accidentes graves en otros sitios, y tenían cierta fascinación macabrosa. Uno de ellos fue sobre un trabajador del DOE que fue completamente incinerado por la explosión creada cuando insertó un amperímetro ordinario de Radio Shack en un circuito de alta corriente. Estimaciones posteriores mostraron que probablemente el calor fue tan intenso que la explosión fue una bola de plasma —un gas tan caliente que sus átomos han sido ionizados.

k/Ejemplo 20.

Ejemplo 20: Un circuito complicado

\(\triangleright\)Las siete resistencias en el panel izquierdo de la figura k son idénticas. Inicialmente, el interruptor S está abierto como se muestra en la figura, y la corriente a través de la resistencia A está\(I_\text{o}\). Luego se cierra el interruptor. Encuentre la corriente a través de la resistencia B, después de cerrar el interruptor, en términos de\(I_\text{o}\). \(\triangleright\)El segundo panel muestra el circuito redibujado por simplicidad, en la condición inicial con el interruptor abierto. Cuando el interruptor está abierto, no puede fluir corriente a través de la resistencia central, por lo que también podemos ignorarlo. También he redibujado los cruces, sin cambiar lo que está conectado con qué. Este es el tipo de reorganización mental que eventualmente aprenderás a hacer automáticamente a partir de la experiencia con el análisis de circuitos. La versión redibujada hace que sea más fácil ver lo que sucede con la corriente. La carga se conserva, por lo que cualquier carga que fluya más allá del punto 1 en el circuito también debe fluir más allá de los puntos 2 y 3. Esto hubiera sido más difícil de razonar al aplicar la regla de cruce a la versión original, que parece tener nueve cruces separados. En la nueva versión, también está claro que el circuito tiene mucha simetría. Podríamos voltear cada par paralelo de resistencias idénticas sin cambiar lo que está conectado a qué, así queda claro que las caídas de tensión y las corrientes deben ser iguales para los miembros de cada par. También podemos probar esto usando la regla de bucle. La regla de bucle dice que las dos caídas de voltaje en el bucle 4 deben ser iguales, y de manera similar para los bucles 5 y 6. Dado que las resistencias obedecen a la ley de Ohm, las caídas de voltaje iguales a través de ellas también implican corrientes iguales. Eso significa que cuando la corriente en el punto 1 llega a la unión superior, exactamente la mitad de ella pasa por cada resistencia. Entonces la corriente se reúne a las 2, se divide entre el siguiente par, y así sucesivamente. Concluimos que cada una de las seis resistencias en el circuito experimenta la misma caída de voltaje y la misma corriente. Aplicando la regla de bucle al bucle 7, encontramos que la suma de las tres caídas de voltaje a través de las tres resistencias de la izquierda es igual al voltaje de la batería\(V\), por lo que cada resistencia en el circuito experimenta una caída de voltaje\(V/3\). Dejando\(R\) reposar la resistencia de una de las resistencias, encontramos que la corriente a través de la resistencia B, que es la misma que las corrientes a través de todas las demás, viene dada por\(I_\text{o}=V/3R\). Pasamos ahora al caso donde el interruptor está cerrado, como se muestra en el tercer panel. El voltaje de la batería es el mismo que antes, y la resistencia de cada resistor es la misma, por lo que aún podemos usar los mismos símbolos\(V\) y\(R\) para ellos. Ya no es cierto, sin embargo, que cada resistor sienta una caída de voltaje\(V/3\). La resistencia equivalente de todo el circuito es\(R/2+R/3+R/2=4R/3\), por lo que la corriente total extraída de la batería es\(3V/4R\). En el grupo medio de resistencias, esta corriente se divide en tres vías, por lo que la nueva corriente a través de B es\((1/3)(3V/4R)=V/4R=3I_\text{o}/4\). Interpretando este resultado, vemos que proviene de dos efectos que cancelan parcialmente. Cerrar el interruptor reduce la resistencia equivalente del circuito al dar a la carga otra forma de fluir, y aumenta la cantidad de corriente extraída de la batería. La resistencia B, sin embargo, solo obtiene una participación de 1/3 de esta corriente mayor, no 1/2. El segundo efecto resulta ser mayor que el primero y, por lo tanto, la corriente a través de la resistencia B disminuye sobre todo.

Pregunta de Discusión

◊ Hemos establecido la regla de bucle en forma simétrica donde una serie de caídas de voltaje se suma a cero. Para ello, tuvimos que definir una forma estándar de conectar el voltímetro al circuito para que los signos más y menos salieran bien. Supongamos que deseamos reafirmar la regla de cruce de una manera simétrica similar, de manera que en lugar de equiparar la corriente que entra a la corriente que sale, simplemente establece que una cierta suma de corrientes en un cruce suma cero. ¿Qué forma estándar de insertar el amperímetro tendríamos que utilizar para hacer que esto funcione?

Colaboradores

Template:ContribCrowell