14.1: Reglas de Aleatoriedad

• Dado por un instante una inteligencia que podría comprender todas las fuerzas por las que se anima la naturaleza y las respectivas posiciones de las cosas que la componen... nada sería incierto, y el futuro como el pasado se expondría ante sus ojos. — Pierre Simon de Laplace, 1776
• La energía producida por el átomo es algo muy pobre. Cualquiera que espere una fuente de poder de la transformación de estos átomos está hablando de alcohol ilegal. — Ernest Rutherford, 1933
• La Mecánica Cuántica es muy imponente. Pero una voz interior me dice que todavía no es la verdad final. La teoría rinde mucho, pero apenas nos acerca al secreto del Viejo. En todo caso, estoy convencido de que Él no juega a los dados. — Albert Einstein

Por muy radical que pareciera a sus contemporáneos el universo relojero de Newton, a principios del siglo XX se había convertido en una especie de dogma con suficiencia aceptado. Por suerte para nosotros, esta imagen determinista del universo se descompone a nivel atómico. La demostración más clara de que las leyes de la física contienen elementos de aleatoriedad está en el comportamiento de los átomos radiactivos. Escoge dos átomos idénticos de un isótopo radiactivo, digamos el uranio 238 de origen natural, y míralos cuidadosamente. Decaerán en diferentes momentos, a pesar de que no hubo diferencia en su comportamiento inicial.

Estaríamos en grandes problemas si el comportamiento de estos átomos fuera tan predecible como se esperaba en la visión del mundo newtoniana, porque la radiactividad es una fuente importante de calor para nuestro planeta. En realidad, cada átomo elige un momento aleatorio en el que liberar su energía, resultando en un agradable efecto de calentamiento constante. La tierra sería un planeta mucho más frío si solo la luz del sol la calentara y no la radiactividad. Probablemente no habría volcanes, y los océanos nunca habrían sido líquidos. Los respiraderos geotérmicos de aguas profundas en los que la vida evolucionó por primera vez nunca habrían existido. Pero habría una consecuencia aún peor si la radiactividad fuera determinista: después de unos pocos miles de millones de años de paz, todos los 238 átomos de uranio de nuestro planeta presumiblemente escogerían el mismo momento para decaer. La enorme cantidad de energía nuclear almacenada, en lugar de extenderse a lo largo de eones, sería liberada en un instante, soplando todo nuestro planeta a Kingdom Come. ¹

Figura\(\PageIndex{1}\): En 1980, Estados Unidos continental obtuvo su primer sabor del vulcanismo activo en la memoria reciente con la erupción del monte St. Helens.

La nueva versión de la física, incorporando ciertos tipos de aleatoriedad, se llama física cuántica (por razones que quedarán claras más adelante). Representaba una ruptura tan dramática con la tradición anterior, determinista, que todo lo que vino antes se considera “clásico”, incluso la teoría de la relatividad. Este capítulo es una introducción básica a la física cuántica.

Ejercicio\(\PageIndex{1}\)

Dije “Elige dos átomos idénticos de un isótopo radiactivo”. ¿Dos átomos son realmente idénticos? Si sus electrones están orbitando el núcleo, ¿podemos distinguir cada átomo por la disposición particular de sus electrones en algún instante en el tiempo?

Responder

Agrega textos aquí. No elimine primero este texto.

13.1.1 La aleatoriedad no es aleatoria

El disgusto de Einstein por la aleatoriedad, y su asociación del determinismo con la divinidad, se remonta a la concepción de la Ilustración del universo como una gigantesca pieza de relojería que solo tuvo que ser puesta en movimiento inicialmente por el Constructor. Muchos de los fundadores de la mecánica cuántica estaban interesados en posibles vínculos entre la física y el pensamiento religioso y filosófico oriental y occidental, pero cada persona educada tiene un concepto diferente de religión y filosofía. Bertrand Russell remarcó: “Sir Arthur Eddington deduce la religión del hecho de que los átomos no obedecen las leyes de las matemáticas. Sir James Jeans lo deduce del hecho de que lo hacen”.

El ingenio de Russell, que implica incorrectamente que las matemáticas no pueden describir la aleatoriedad, nos recuerdan lo importante que es no simplificar demasiado esta cuestión de aleatoriedad. No se debe simplemente suponer: “Bueno, todo es aleatorio, puede pasar cualquier cosa”. Por un lado, ciertas cosas simplemente no pueden suceder, ni en la física clásica ni en la física cuántica. Las leyes de conservación de la masa, la energía, el impulso y el momento angular siguen siendo válidas, por lo que, por ejemplo, los procesos que crean energía de la nada no son solo improbables según la física cuántica, son imposibles.

Se puede hacer una analogía útil con el papel de la aleatoriedad en la evolución. Darwin no fue el primer biólogo en sugerir que las especies cambiaron durante largos períodos de tiempo. Sus dos nuevas ideas fundamentales fueron que (1) los cambios surgieron a través de la variación genética aleatoria, y (2) se conservarían los cambios que potenciaban la capacidad del organismo para sobrevivir y reproducirse, mientras que los cambios desadaptativos serían eliminados por la selección natural. Los que dudan de la evolución suelen considerar solo el primer punto, sobre la aleatoriedad de la variación natural, pero no el segundo punto, sobre la acción sistemática de la selección natural. Hacen declaraciones como, “el desarrollo de un organismo complejo como el Homo sapiens vía azar sería como un torbellino soplando a través de un depósito de chatarra y ensamblando espontáneamente un jumbo jet a partir de la chatarra”. La falla en este tipo de razonamientos es que ignora las restricciones deterministas sobre los resultados de procesos aleatorios. Que un átomo viole la conservación de la energía no es más probable que la conquista del mundo por parte de los chimpancés el próximo año.

Ejercicio\(\PageIndex{1}\)

Los economistas suelen comportarse como aspirantes a físicos, probablemente porque parece prestigioso hacer cálculos numéricos en lugar de hablar de relaciones humanas y organizaciones como otros científicos sociales. Su esfuerzo por hacer que la economía funcione como la física newtoniana se extiende a un uso paralelo de metáforas mecánicas, como en el concepto de la oferta y la demanda de un mercado que actúa como una máquina autoajustable, y la idealización de las personas como autómatas económicos que constantemente se esfuerzan por maximizar su propia riqueza. ¿Qué evidencia hay de aleatoriedad en lugar de determinismo mecánico en economía?

Responder

Discusión Pregunta - no se da respuesta.

13.1.2 Cálculo de aleatoriedad

También debes darte cuenta de que aunque algo sea aleatorio, todavía podemos entenderlo, y aún podemos calcular las probabilidades numéricamente. En otras palabras, los físicos son buenos corredores de apuestas. Una buena casa de apuestas puede calcular las probabilidades de que un caballo gane una carrera con mucha más precisión que una inexperta, pero sin embargo no puede predecir lo que sucederá en una carrera en particular.

Como ilustración de una técnica general para calcular probabilidades, supongamos que está jugando una máquina tragaperras de 25 centavos. Cada una de las tres ruedas tiene una oportunidad en diez de llegar a una cereza. Si las tres ruedas suben cerezas, ganas $100. Aunque los resultados de cualquier ensayo en particular son aleatorios, puedes hacer ciertas predicciones cuantitativas. Primero, puedes calcular que tus probabilidades de ganar en cualquier juicio dado son\(1/10\times1/10\times1/10=1/1000=0.001\). Aquí, estoy representando las probabilidades como números del 0 al 1, lo que es más claro que declaraciones como “Las probabilidades son 999 a 1”, y facilita los cálculos. Una probabilidad de 0 representa algo imposible, y una probabilidad de 1 representa algo que definitivamente sucederá.

Además, puedes decir que cualquier prueba dada es igualmente probable que resulte en una victoria, y no importa si has ganado o perdido en juegos anteriores. Matemáticamente, decimos que cada prueba es estadísticamente independiente, o que los juegos separados no están correlacionados. La mayoría de los jugadores están equivocadamente convencidos de que, por el contrario, los juegos de azar están correlacionados. Si han estado jugando a una máquina tragaperras todo el día, están convencidos de que se está “preparando para pagar”, y no quieren que nadie más juegue a la máquina y “agote” el premio mayor que “tienen que venir”. En otras palabras, están afirmando que una serie de pruebas en la máquina tragaperras está negativamente correlacionada, que perder ahora te hace más probable que ganes más tarde. Los jugadores de Craps afirman que debes ir a una mesa donde la persona que tira los dados esté “caliente”, porque es probable que siga rodando buenos números. Los jugadores de dados, entonces, creen que las tiradas de los dados están correlacionadas positivamente, que ganar ahora te hace más probable que ganes más tarde.

Mi método para calcular la probabilidad de ganar en la máquina tragaperras fue un ejemplo de la siguiente regla importante para los cálculos basados en probabilidades independientes:

La ley de las probabilidades independientes

Si la probabilidad de que ocurra un evento es\(P_A\), y la probabilidad de que ocurra un segundo evento estadísticamente independiente es\(P_B\), entonces la probabilidad de que ambos ocurran es producto de las probabilidades,\(P_AP_B\). Si hay más de dos eventos involucrados, simplemente sigues multiplicando.

Esto puede tomarse como la definición de independencia estadística.

Tenga en cuenta que esto solo aplica a las probabilidades independientes. Por ejemplo, si tienes un centavo y un centavo en el bolsillo, y sacas uno al azar, hay una probabilidad de 0.5 de que sea el níquel. Si luego reemplazas la moneda y vuelves a sacar una al azar, nuevamente hay una probabilidad de 0.5 de subir con el níquel, porque las probabilidades son independientes. Por lo tanto, existe una probabilidad de 0.25 de que obtendrá el níquel en ambas ocasiones.

Supongamos en cambio que no reemplaces la primera moneda antes de sacar la segunda. Entonces estás obligado a sacar la otra moneda la segunda vez, y no hay forma de que puedas sacar el níquel dos veces. Ante esta situación, los dos juicios no son independientes, porque el resultado del primer juicio incide en el segundo. No se aplica la ley de probabilidades independientes, y la probabilidad de obtener el níquel dos veces es cero, no 0.25.

Los experimentos han demostrado que en el caso de la desintegración radiactiva, la probabilidad de que algún núcleo se descomponga durante un intervalo de tiempo determinado no se ve afectada por lo que le está sucediendo a los otros núcleos, y tampoco está relacionada con cuánto tiempo ha pasado sin descomponerse. La primera observación tiene sentido, porque los núcleos están aislados unos de otros en los centros de sus respectivos átomos, y por lo tanto no tienen forma física de influir entre sí. El segundo hecho también es razonable, ya que todos los átomos son idénticos. Supongamos que quisiéramos creer que ciertos átomos eran “extra duros”, como lo demuestra su historia de pasar un tiempo inusualmente largo sin descomponerse. Esos átomos tendrían que ser diferentes de alguna manera física, pero nunca nadie ha logrado detectar diferencias entre los átomos. No hay manera de que un átomo sea cambiado por las experiencias que tiene en su vida.

La Ley de Probabilidades Independientes nos dice usar la multiplicación para calcular la probabilidad de que tanto A como B sucedan, asumiendo que las probabilidades son independientes. ¿Qué pasa con la probabilidad de un “o” en lugar de un “y”? Si dos eventos A y\(B\) son mutuamente excluyentes, entonces la probabilidad de que ocurra uno u otro es la suma\(P_A+P_B\). Por ejemplo, un jugador de bolos podría tener un 30% de probabilidad de recibir un strike (derribando los diez pines) y un 20% de probabilidad de derribar nueve de ellos. Por lo tanto, la probabilidad del jugador de lanzador de derribar nueve o diez alfileres es del 50%.

No tiene sentido agregar probabilidades de cosas que no son mutuamente excluyentes, es decir, que ambas podrían suceder. Digamos que tengo un 90% de posibilidades de almorzar en un día cualquiera, y un 90% de posibilidades de cenar. La probabilidad de que coma ya sea almuerzo o cena no es del 180%.

Normalización

Si giro un globo terráqueo y escojo aleatoriamente un punto en él, tengo aproximadamente un 70% de probabilidad de elegir un punto que esté en un océano y un 30% de probabilidad de escoger un punto en tierra. La probabilidad de recoger agua o tierra es\(70%+30%=100%\). El agua y la tierra son mutuamente excluyentes, y no hay otras posibilidades, por lo que las probabilidades tuvieron que sumar hasta el 100%. Funciona igual si hay más de dos posibilidades: si puedes clasificar todos los resultados posibles en una lista de resultados mutuamente excluyentes, entonces todas las probabilidades tienen que sumar hasta 1, o 100%. Esta propiedad de probabilidades se conoce como normalización.

Figura\(\PageIndex{2}\): Normalización: la probabilidad de recoger tierra más la probabilidad de recoger agua suma 1.

Promedios

Otra forma de lidiar con la aleatoriedad es tomar promedios. El casino sabe que a la larga, el número de veces que ganes será aproximadamente igual al número de veces que juegues multiplicado por la probabilidad de ganar. En el juego de máquinas tragamonedas descrito en la página 823, donde la probabilidad de ganar es 0.001, si pasas una semana jugando, y pagas 2500 dólares para jugar 10,000 veces, es probable que ganes unas 10 veces\((10,000\times0.001=10)\), y recaudes $1000. En promedio, el casino obtendrá una ganancia de 1500 dólares de usted. Este es un ejemplo de la siguiente regla.

Regla para calcular promedios

Si realiza ensayos\(N\) idénticos, estadísticamente independientes, y la probabilidad de éxito en cada ensayo es\(P\), entonces en promedio, el número total de ensayos exitosos será\(NP\). Si\(N\) es lo suficientemente grande, el error relativo en esta estimación se volverá pequeño.

La afirmación de que la regla para calcular promedios se vuelve cada vez más precisa para cada vez más grandes\(N\) (conocida popularmente como la “ley de los promedios”) a menudo proporciona un principio de correspondencia que conecta la física clásica y cuántica. Por ejemplo, la cantidad de energía producida por una central nuclear no es aleatoria en ningún nivel detectable, porque el número de átomos en el reactor es muy grande. En general, el comportamiento aleatorio a nivel atómico tiende a promediar cuando consideramos grandes números de átomos, razón por la cual la física parecía determinista antes de que los físicos aprendieran técnicas para estudiar los átomos individualmente.

Podemos lograr una gran precisión con promedios en física cuántica porque podemos usar átomos idénticos para reproducir exactamente la misma situación muchas veces. Si estuviéramos apostando a caballos o dados, estaríamos mucho más limitados en nuestra precisión. Después de mil carreras, el caballo estaría listo para retirarse. Después de un millón de tiradas, los dados estarían gastados.

Ejercicio\(\PageIndex{1}\)

¿Cuáles de las siguientes cosas deben ser independientes, cuáles podrían ser independientes y cuáles definitivamente no son independientes? (1) la probabilidad de hacer con éxito dos tiros libres seguidos en básquetbol; (2) la probabilidad de que llueva mañana en Londres y la probabilidad de que llueva el mismo día en cierta ciudad en una galaxia lejana; (3) tu probabilidad de morir hoy y de morir mañana.

Responder

Contesta en la parte posterior de la versión PDF del libro.

Ejercicio\(\PageIndex{1}\) Discussion Questions

Figura\(\PageIndex{3}\): ¿Por qué los dados son aleatorios?

• La física newtoniana es una aproximación esencialmente perfecta para describir el movimiento de un par de dados. Si la física newtoniana es determinista, ¿por qué consideramos que el resultado de lanzar dados es aleatorio?
• ¿Por qué no es válido definir aleatoriedad diciendo que la aleatoriedad es cuando todos los resultados son igualmente probables?
• La secuencia de dígitos 1212121212121212 parece claramente no aleatoria, y 41592653589793 parece aleatoria. Esta última secuencia, sin embargo, es la forma decimal de pi, comenzando por el tercer dígito. Hay una historia sobre el matemático indio Ramanujan, un prodigio autodidacta, que un amigo vino a visitarlo en un taxi, y remarcó que el número de la cabina, 1729, parecía relativamente poco interesante. Ramanujan respondió que por el contrario, era muy interesante porque era el número más pequeño que se podía representar de dos maneras distintas como la suma de dos cubos. El autor argentino Jorge Luis Borges escribió un cuento corto llamado “La biblioteca de Babel”, en el que imaginaba una biblioteca que contenía todos los libros que posiblemente podrían escribirse usando las letras del alfabeto. Incluiría un libro que contenía solo la repetida letra “a”; todas las tragedias griegas antiguas conocidas hoy, todas las tragedias griegas perdidas y millones de tragedias griegas que nunca se escribieron realmente; tu propia historia de vida, y varias versiones incorrectas de tu propia historia de vida; e innumerables antologías que contiene un cuento llamado “La Biblioteca de Babel”. Por supuesto, si escogieras un libro de las estanterías de la biblioteca, seguramente parecería una secuencia sin sentido de letras y puntuación, pero siempre es posible que el libro aparentemente sin sentido sea un guión de ciencia ficción escrito en el lenguaje de una tribu neandertal, o la letra a un conjunto de canciones de amor incomparablemente bellas escritas en un lenguaje que nunca existió. A la vista de estos ejemplos, ¿qué significa realmente decir que algo es aleatorio?

Responder

Agrega textos aquí. No elimine primero este texto.

13.1.3 Distribuciones de probabilidad

Hasta ahora hemos hablado de procesos aleatorios que tienen sólo dos resultados posibles: sí o no, ganar o perder, encendido o apagado. De manera más general, un proceso aleatorio podría tener un resultado que es un número. Algunos procesos producen enteros, como cuando se rueda un dado y se obtiene un resultado del uno al seis, pero algunos no se restringen a números enteros, por ejemplo el número de segundos que existirá un átomo de uranio-238 antes de sufrir desintegración radiactiva.

Considera tirar de un dado. Si el dado es “honesto”, entonces esperamos que los seis valores sean igualmente probables. Dado que las seis probabilidades deben sumar hasta 1, entonces la probabilidad de que algún valor en particular suba debe ser 1/6. Podemos resumir esto en una gráfica (Figura\(\PageIndex{4a}\)). Las áreas bajo la curva se pueden interpretar como probabilidades totales. Por ejemplo, el área bajo la curva de 1 a 3 es\(1/6+1/6+1/6=1/2\), por lo que la probabilidad de obtener un resultado de 1 a 3 es 1/2. La función que se muestra en la gráfica se llama distribución de probabilidad.

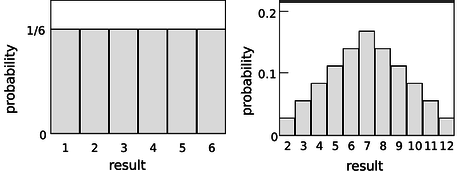
Figura\(\PageIndex{4}\): (a) Distribución de probabilidad para el resultado de enrollar una sola matriz. (b) Hacer rodar dos dados y sumarlos.

La figura\(\PageIndex{4b}\) muestra las probabilidades de diversos resultados obtenidos al rodar dos dados y sumarlos juntos, como en el juego de dados. Las probabilidades no son todas iguales. Hay una pequeña probabilidad de obtener un dos, por ejemplo, porque sólo hay una manera de hacerlo, rodando un uno y luego otro. La probabilidad de rodar un siete es alta porque hay seis formas diferentes de hacerlo: 1+6, 2+5, etc.

Si el número de posibles resultados es grande pero finito, por ejemplo el número de pelos en un perro, la gráfica comenzaría a verse como una curva suave en lugar de un zigurat.

¿Qué pasa con las distribuciones de probabilidad para números aleatorios que no son enteros? Ya no podemos hacer una gráfica con probabilidad en el\(y\) eje, porque la probabilidad de obtener un número exacto dado suele ser cero. Por ejemplo, hay cero probabilidades de que un átomo radiactivo dure exactamente 3 segundos, ya que hay infinitamente muchos resultados posibles que están cerca de 3 pero no exactamente tres: 2.9999999999999999999996876876587658465436, por ejemplo. No suele tener sentido, por lo tanto, hablar de la probabilidad de un solo resultado numérico, pero sí tiene sentido hablar de la probabilidad de un cierto rango de resultados. Por ejemplo, la probabilidad de que un átomo dure más de 3 y menos de 4 segundos es algo perfectamente razonable de discutir. Todavía podemos resumir la información de probabilidad en una gráfica, y aún podemos interpretar las áreas bajo la curva como probabilidades.

Pero el\(y\) eje ya no puede ser una escala de probabilidad sin unidades. En la desintegración radiactiva, por ejemplo, queremos que el\(x\) eje tenga unidades de tiempo, y queremos que las áreas bajo la curva sean probabilidades sin unidades. El área de un solo cuadrado en el papel cuadriculado es entonces

\[\begin{gather*} \text{(unitless area of a square)} \\ = \text{(width of square with time units)}\\ \times \text{(height of square)} . \end{gather*}\]

Si las unidades van a cancelar, entonces la altura del cuadrado evidentemente debe ser una cantidad con unidades de tiempo inverso. Es decir, el\(y\) eje de la gráfica debe interpretarse como probabilidad por unidad de tiempo, no como probabilidad. La figura\(\PageIndex{5}\) muestra otro ejemplo, una distribución de probabilidad para la altura de las personas. Este tipo de curva en forma de campana es bastante común. \

Figura\(\PageIndex{5}\): Distribución de probabilidad para la estatura de adultos humanos (no datos reales).

Ejercicio\(\PageIndex{1}\)

Compare el número de personas con alturas en el rango de 130-135 cm con el número en el rango 135-140

Responder

(respuesta en la parte posterior de la versión PDF del libro).

Ejemplo\(\PageIndex{1}\): Looking for tall basketball players

Un determinado país con una gran población quiere encontrar gente muy alta para estar en su equipo olímpico de basquetbol y dar un golpe contra el imperialismo occidental. De un grupo de\(10^8\) personas que tienen la edad y el género adecuados, ¿cuántas es probable que encuentren que tengan más de 225 cm (7 pies 4 pulgadas) de altura? La Figura g da un primer plano de la “cola” de la distribución mostrada previamente en la Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\)

El área sombreada bajo la curva representa la probabilidad de que una persona determinada sea lo suficientemente alta. Cada rectángulo representa una probabilidad de\(0.2\times10^{-7}\ \text{cm}^{-1} \times 1\ \text{cm}=2\times10^{-8}\). Hay alrededor de 35 rectángulos cubiertos por el área sombreada, por lo que la probabilidad de tener una altura mayor a 225 cm es\(7\times10^{-7}\), o poco menos de uno en un millón. Usando la regla para calcular promedios, el promedio, o número esperado de personas así de alto es\((10^8)\times(7\times10^{-7})=70\).

Promedio y ancho de una distribución de probabilidad

Si el próximo marciano que conoces te pregunta: “¿Qué altura tiene un humano adulto? ”, probablemente responderá con una declaración sobre la estatura humana promedio, como “Oh, alrededor de 5 pies y 6 pulgadas”. Si quisieras explicar un poco más, podrías decir: “Pero eso es sólo un promedio. La mayoría de las personas tienen entre 5 pies y 6 pies de altura”. Sin molestarse en dibujar la curva de campana relevante para tu nuevo conocido extraterrestre, has resumido la información relevante dando un promedio y un rango típico de variación.

Figura\(\PageIndex{6}\): El promedio de una distribución de probabilidad.

El promedio de una distribución de probabilidad puede definirse geométricamente como la posición horizontal en la que podría equilibrarse si se construyera de cartón. Una medida numérica conveniente de la cantidad de variación sobre el promedio, o cantidad de incertidumbre, es el ancho completo a la mitad del máximo, o FWHM, que se muestra en la Figura\(\PageIndex{7}\).

Figura\(\PageIndex{7}\): El ancho completo a la mitad del máximo (FWHM) de una distribución de probabilidad.

Se podría decir mucho más sobre este tema, y de hecho un curso introductorio de estadística podría dedicar meses a formas de definir el centro y el ancho de una distribución. En lugar de alimentarte a la fuerza con detalles matemáticos o técnicas para calcular estas cosas, quizás sea más relevante señalar simplemente que existen diversas formas de definirlas, e inocularte contra el mal uso de ciertas definiciones.

El promedio no es la única manera posible de decir cuál es un valor típico para una cantidad que puede variar aleatoriamente; otra definición posible es la mediana, definida como el valor que se excede con 50% de probabilidad. Al discutir los ingresos de las personas que viven en un determinado pueblo, el promedio podría ser muy engañoso, ya que puede verse afectado masivamente si un solo residente de la localidad es Bill Gates. Tampoco es el FWHM la única forma posible de afirmar la cantidad de variación aleatoria; otra forma posible de medirla es la desviación estándar (definida como la raíz cuadrada de la desviación cuadrada promedio del valor promedio).

13.1.4 Decaimiento exponencial y vida media

La mayoría de la gente sabe que la radiactividad “dura cierta cantidad de tiempo”, pero esa simple afirmación deja fuera mucho. Como ejemplo, considere el siguiente procedimiento médico utilizado para diagnosticar la función tiroidea. Una cantidad muy pequeña del isótopo\(^{131}\text{I}\), producida en un reactor nuclear, es alimentada o inyectada en el paciente. Los sistemas bioquímicos del cuerpo tratan a este isótopo artificial y radiactivo exactamente igual que\(^{127}\text{I}\), que es el único tipo de origen natural. (Nutricionalmente, el yodo es un oligoelemento necesario. El yodo que se introduce en el cuerpo se excreta parcialmente, pero el resto se concentra en la glándula tiroides. A la sal yodada se le ha agregado yodo para prevenir la deficiencia nutricional conocida como bocios, en la que se hincha la tiroides hambrienta de yodo). A medida que\(^{131}\text{I}\) sufre una desintegración beta, emite electrones, neutrinos y rayos gamma. Los rayos gamma se pueden medir mediante un detector que pasa sobre el cuerpo del paciente. A medida que el yodo radiactivo se concentra en la tiroides, la cantidad de radiación gamma proveniente de la tiroides aumenta, y la emitida por el resto del cuerpo se reduce. La velocidad a la que el yodo se concentra en la tiroides le dice al médico sobre la salud de la tiroides.

Si alguna vez te sometes a este procedimiento, alguien presumiblemente te explicará un poco sobre la radiactividad, para disipar tus temores de que te convertirás en el Increíble Hulk, o que tu próximo hijo tenga un número inusual de extremidades. Dado que el yodo permanece en tu tiroides durante mucho tiempo una vez que llegue ahí, una cosa que querrás saber es si tu tiroides se va a volver radioactiva para siempre. Quizá solo te digan que la radiactividad “sólo dura una cierta cantidad de tiempo”, pero ahora podemos llevar a cabo una derivación cuantitativa de cómo la radiactividad realmente va a desaparecer.

\(P_{surv}(t)\)Sea la probabilidad de que un átomo de yodo sobreviva sin descomponerse por un periodo de al menos\(t\). Se ha medido experimentalmente que la mitad de todos los\(^{131}\text{I}\) átomos se descomponen en 8 horas, así que tenemos

\[ P_{surv}(8\ \text{hr}) = 0.5 . \]

Ahora usando la ley de probabilidades independientes, la probabilidad de sobrevivir por 16 horas equivale a la probabilidad de sobrevivir durante las primeras 8 horas multiplicada por la probabilidad de sobrevivir por las segundas 8 horas,

\[\begin{align*} P_{surv}(16\ \text{hr}) &= 0.50\times0.50 \\ &= 0.25 . \end{align*}\]

Del mismo modo tenemos

\[\begin{align*} P_{surv}(24\ \text{hr}) &= 0.50\times0.5\times0.5 \\ &= 0.125 . \end{align*}\]

Generalizando a partir de este patrón, la probabilidad de sobrevivir por cualquier tiempo\(t\) que sea un múltiplo de 8 horas es

\[ P_{surv}(t) = 0.5^{t/8\ \text{hr}} . \]

Ahora sabemos cómo encontrar la probabilidad de supervivencia a intervalos de 8 horas, pero ¿qué pasa con los puntos en el tiempo intermedios? ¿Cuál sería la probabilidad de sobrevivir 4 horas? Bueno, usando de nuevo la ley de probabilidades independientes, tenemos

\[ P_{surv}(8\ \text{hr}) = P_{surv}(4\ \text{hr}) \times P_{surv}(4\ \text{hr}) , \]

que se puede reorganizar para dar

\[\begin{align*} P_{surv}(4\ \text{hr}) &= \sqrt{P_{surv}(8\ \text{hr})} \\ &= \sqrt{0.5} \\ &= 0.707 . \end{align*}\]

Esto es exactamente lo que hubiéramos encontrado simplemente enchufándonos\(P_{surv}(t)=0.5^{t/8\ \text{hr}}\) e ignorando la restricción a múltiplos de 8 horas. Dado que 8 horas es la cantidad de tiempo que se requiere para que la mitad de los átomos se descomponga, se le conoce como la vida media, escrita\(t_{1/2}\). La regla general es la siguiente:

\[ \underbrace{P_{surv}(t) = 0.5^{t/t_{1/2}}}_{\text{Exponential Decay Equation}} \]

Usando la regla para calcular promedios, también podemos encontrar el número de átomos,\(N(t)\), quedando en una muestra a la vez\(t \):

\[ N(t) = N(0) \times 0.5^{t/t_{1/2}} \]

Ambas ecuaciones tienen gráficas que parecen exponenciales atenuantes, como en el siguiente ejemplo.

Ejemplo\(\PageIndex{2}\): Radioactive contamination at Chernobyl

Uno de los isótopos radiactivos más peligrosos liberados por el desastre de Chernobyl en 1986 fue\(^{90}\text{Sr}\), cuya vida media es de 28 años. a) ¿Cuánto tiempo pasará antes de que la contaminación se reduzca a una décima parte de su nivel original? b) Si se liberara un total de\(10^{27}\) átomos, ¿cuánto tiempo pasaría antes de que no quedara ni un solo átomo?

Solución

(a) Queremos saber la cantidad de tiempo que un\(^{90}\text{Sr}\) núcleo tiene una probabilidad de 0.1 de sobrevivir. Comenzando con la fórmula de decaimiento exponencial,

\[ P_{surv} = 0.5^{t/t_{1/2}} , \nonumber \]

queremos resolver para\(t\). Tomando logaritmos naturales de ambos lados,

\[ \ln P = \frac{t}{t_{1/2}}\ln 0.5 , \nonumber\]

entonces

\[ t = \frac{t_{1/2}}{\ln 0.5}\ln P \nonumber \]

El enchufar\(P=0.1\) y\(t_{1/2}=28\) años, tenemos\(t=93\) años.

(b) Esto es igual que la primera parte, pero\(P=10^{-27}\). El resultado es de unos 2500 años.

Ejemplo\(\PageIndex{3}\): \(^{14}\text{C}\) Dating

Casi todo el carbono en la Tierra lo es\(^{12}\text{C}\), pero no del todo. El isótopo\(^{14}\text{C}\), con una vida media de 5600 años, es producido por los rayos cósmicos en la atmósfera. Se descompone naturalmente, pero se repone a tal ritmo que la fracción de\(^{14}\text{C}\) en la atmósfera se mantiene constante, a\(1.3\times10^{-12}\). Las plantas y los animales vivos toman tanto como\(^{12}\text{C}\)\(^{14}\text{C}\) de la atmósfera e incorporan ambos en sus cuerpos. Una vez que el organismo vivo muere, ya no toma átomos de C de la atmósfera, y la proporción de disminuye\(^{14}\text{C}\) gradualmente a medida que sufre desintegración radiactiva. Este efecto puede ser utilizado para encontrar la edad de organismos muertos, o artefactos humanos hechos de plantas o animales. La Figura j muestra la curva de decaimiento exponencial de\(^{14}\text{C}\) en diversos objetos. Métodos similares, utilizando isótopos de vida más larga, proporcionaron la primera prueba firme de que la tierra tenía miles de millones de años, no pocos miles como algunos habían afirmado por motivos religiosos.

Figura\(\PageIndex{8}\): Calibración del método de\(^{14}\text{C}\) datación utilizando anillos de árboles y artefactos cuyas edades se conocían por otros métodos. Redibujado de Emilio Segrè, Núcleos y Partículas, 1965.

Tasa de Decaimiento

Si quieres saber cuántas desintegraciones radiactivas ocurren dentro de un intervalo de tiempo\(t\) que dura de vez en cuando\(t+\Delta t\), el enfoque más directo es calcularlo así:

\[\begin{align*} (\text{number of}&\text{ decays between } t \text{ and } t+\Delta t) \\ &= N(t) - N(t+\Delta t) \end{align*}\]

Por lo general nos interesa el caso donde\(\Delta t\) es pequeño comparado con\(t_{1/2}\), y en este caso limitante el cálculo comienza a parecerse exactamente al límite que entra en la definición de la derivada\(dN/dt\). Por lo tanto, es más conveniente hablar sobre la tasa de decaimiento en\(-dN/dt\) lugar del número de desintegraciones en algún intervalo de tiempo finito. Hacer cálculo en la función también\(e^x\) es más fácil que con\(0.5^x\), así que reescribimos la función\(N(t)\) como

\[ N = N(0) e^{-t/\tau} , \]

donde\(\tau=t_{1/2}/\ln 2\) se muestra en el ejemplo 6 en la p. 835 como el tiempo promedio de supervivencia. La tasa de decaimiento es entonces

\[ -\frac{dN}{dt} = \frac{N(0)}{\tau} e^{-t/\tau} . \]

Matemáticamente, diferenciando un exponencial solo devuelve otro exponencial. Físicamente, esto nos está diciendo que a medida que\(N\) cae exponencialmente, la tasa de decaimiento cae a la misma velocidad exponencial, porque un menor\(N\) significa menos átomos que permanecen disponibles para descomponerse.

Ejercicio\(\PageIndex{1}\)

Verifique que ambos lados de la ecuación para la tasa de decaimiento tengan unidades de\(\text{s}^{-1}\), es decir, decae por unidad de tiempo.

Responder

respuesta en la parte posterior de la versión PDF del libro)

Ejemplo\(\PageIndex{4}\): The hot potato

Un físico nuclear con un sentido del humor demente te lanza una caja de puros, gritando “papa caliente”. La etiqueta en la caja dice “contiene\(10^{20}\) átomos de\(^{17}\text{F}\), semivida de 66 s, producido hoy en nuestro reactor a la 1 de la tarde”. Te lleva dos segundos leer la etiqueta, después de lo cual la tiras detrás de algunos ladrillos de plomo y huyes. La hora es la 1:40 p.m. ¿Morirás?

Solución

El tiempo transcurrido desde que se produjo el flúor radiactivo en el reactor fue de 40 minutos, o 2400 s. Por lo tanto, el número de semividas transcurridas es\(t/t_{1/2}= 36\). El número inicial de átomos fue\(N(0)=10^{20}\). El número de desintegraciones por segundo es ahora aproximadamente\(10^7\ \text{s}^{-1}\), por lo que produjo alrededor\(2\times10^7\) de electrones de alta energía mientras lo sostenías en tus manos. A pesar de que veinte millones de electrones suenan como mucho, en realidad no es suficiente para ser peligrosos.

Por cierto, ninguna de las ecuaciones que hemos derivado hasta ahora era la distribución de probabilidad real para el momento en que un átomo radiactivo particular se desintegrará. Esa distribución de probabilidad se encontraría sustituyendo\(N(0)=1\) en la ecuación la tasa de decaimiento.

Preguntas de Discusión

◊ En el procedimiento médico que implica\(^{131}\text{I}\), ¿por qué son los rayos gamma los que se detectan, no los electrones o neutrinos los que también se emiten?

◊ Por 1 s, Fred sostiene en sus manos 1 kg de material radiactivo con una vida media de 1000 años. El jengibre contiene 1 kg de una sustancia diferente, con una vida media de 1 min, por la misma cantidad de tiempo. ¿Se pusieron en igual peligro, o no?

◊ ¿Cómo lo interpretarías si calcularas\(N(t)\), y encontraras que era menos de uno?

◊ ¿La vida media depende de la cantidad de sustancia que tengas? ¿El tiempo esperado hasta que la muestra decae por completo depende de la cantidad de sustancia que tenga?

13.1.5 Aplicaciones de Cálculo

El área bajo la distribución de probabilidad es, por supuesto, una integral. Si llamamos al número aleatorio\(x\) y a la distribución de probabilidad\(D(x)\), entonces la probabilidad que\(x\) se encuentra en un cierto rango viene dada por

\[ \text{(probability of $a\le x \le b$)}=\int_a^b D(x) dx . \]

¿Y los promedios? Si\(x\) tuviera un número finito de valores igualmente probables, simplemente los sumaríamos y dividiríamos por cuántos teníamos. Si no fueran igualmente probables, haríamos el promedio ponderado\(x_1P_1+x_2P_2+\)... Pero necesitamos generalizar esto a una variable\(x\) que pueda asumir cualquiera de un continuo de valores. La versión continua de una suma es una integral, por lo que el promedio es

\[ \text{(average value of $x$)} = \int x D(x) dx , \]

donde la integral está sobre todos los valores posibles de\(x\).

Ejemplo\(\PageIndex{5}\): Probability distribution for radioactive decay

Aquí hay una justificación rigurosa para la afirmación en la subsección 13.1.4 de que la distribución de probabilidad para la desintegración radiactiva se encuentra sustituyendo\(N(0)=1\) en la ecuación la tasa de desintegración. Sabemos que la distribución de probabilidad debe ser de la forma

\[ D(t) = k 0.5^{t/t_{1/2}} , \]

donde\(k\) es una constante que necesitamos determinar. Se garantiza que el átomo se descompondrá eventualmente, así que la normalización nos da

\[\begin{align*} \text{(probability of $0\le t \lt \infty$)} &= 1 \\ &= \int_0^\infty D(t) dt . \end{align*}\]

La integral se evalúa más fácilmente convirtiendo la función en un exponencial con\(e\) como base

\[\begin{align*} D(t) &= k \exp\left[\ln\left(0.5^{t/t_{1/2}}\right)\right] \\ &= k \exp\left[\frac{t}{t_{1/2}}\ln 0.5\right] \\ &= k \exp\left(-\frac{\ln 2}{t_{1/2}}t\right) , \end{align*}\]

lo que da una integral de la forma familiar\(\int e^{cx}dx=(1/c)e^{cx}\). Así tenemos

\[ 1 = \left.-\frac{kt_{1/2}}{\ln 2}\exp\left(-\frac{\ln 2}{t_{1/2}}t\right)\right]_0^\infty , \]

lo que da el resultado deseado:

\[ k = \frac{\ln 2}{t_{1/2}} . \]

Ejemplo\(\PageIndex{6}\): Average lifetime

Se podría pensar que la vida media también sería la vida media de un átomo, ya que la mitad de las vidas de los átomos son más cortas y la mitad más largas. Pero la mitad cuyas vidas son más largas incluyen algunas que sobreviven durante muchas vidas medias, y estos raros átomos de larga vida sesgan el promedio. Podemos calcular la vida media de la siguiente manera:

\[ (\text{average lifetime}) = \int_0^\infty t\: D(t)dt \]

Usando el conveniente\(e\) formulario base de nuevo, tenemos

\[ (\text{average lifetime}) = \frac{\ln 2}{t_{1/2}} \int_0^\infty t \exp\left(-\frac{\ln 2}{t_{1/2}}t\right) dt . \]

Esta integral es de una forma que puede ser atacada con integración por partes o buscándolo en una tabla. El resultado es\(\int x e^{cx}dx=\frac{x}{c}e^{cx}-\frac{1}{c^2}e^{cx}\), y el primer término puede ser ignorado para nuestros propósitos porque equivale a cero en ambos límites de integración. Terminamos con

\[\begin{align*} \text{(average lifetime)} &= \frac{\ln 2}{t_{1/2}}\left(\frac{t_{1/2}}{\ln 2}\right)^2 \\ &= \frac{t_{1/2}}{\ln 2} \\ &= 1.443 \: t_{1/2} , \end{align*}\]

que es, como se esperaba, más de una vida media.

Figura\(\PageIndex{9}\): En las últimas décadas, un enorme agujero en la capa de ozono se ha extendido desde la Antártida. Izquierda: Noviembre 1978. Derecha: noviembre de 1992

Colaboradores y Atribuciones

• Template:ContribCrowell