5.1: El Algoritmo Básico
- Page ID
- 125124
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
La mejor manera de entender cómo funciona la eliminación gaussiana es trabajar a través de un ejemplo concreto. Considera el siguiente\(N=3\) problema:
\[\begin{bmatrix}1 &2 &3 \\ 3 &2 &2 \\ 2 &6 &2\end{bmatrix} \begin{bmatrix} x_0 \\ x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix}3 \\ 4 \\ 4\end{bmatrix}.\]
El algoritmo de eliminación gaussiana consta de dos fases distintas: reducción de filas y sustitución por retroceso.
5.1.1 Educación de la fila R
En la fase de reducción de filas del algoritmo, manipulamos la ecuación matricial para que la matriz se vuelva triangular superior (es decir, todas las entradas por debajo de la diagonal son cero). Para lograrlo, observamos que podemos restar una fila de otra, sin alterar la solución. De hecho, podemos restar cualquier múltiplo de una fila.
Eliminaremos (cero) los elementos por debajo de la diagonal en un orden específico: de arriba a abajo a lo largo de cada columna, luego de izquierda a derecha para columnas sucesivas. Para nuestro\(3\times 3\) ejemplo, los elementos que pretendemos eliminar, y el orden en que los eliminaremos, están indicados por los números coloreados\(0\),\(1\), y\(2\) en la siguiente figura:
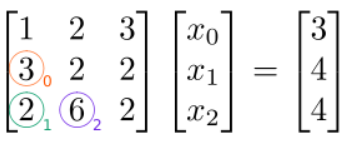
El primer elemento matricial que queremos eliminar es at\((1,0)\) (círculo naranja). Para eliminarlo, restamos, de esta fila, un múltiplo de fila\(0\). Utilizaremos un factor de\(3/1=3\):
\[(3x_0 + 2x_1 + 2x_2) - (3/1)(1x_0 + 2x_1 + 3x_2) = 4 - (3/1) 3\]
El factor de\(3\) que usamos se determina de la siguiente manera: dividimos el elemento matriz en\((1,0)\) (que es el que pretendemos eliminar) por el elemento at\((0,0)\) (que es el que está a lo largo de la diagonal en la misma columna). Como resultado, el término proporcional a\(x_{0}\) desaparece, y obtenemos las siguientes ecuaciones lineales modificadas, que poseen la misma solución:

(Tenga en cuenta que también hemos cambiado la entrada en el vector en el lado derecho, ¡no solo la matriz en el lado izquierdo!) A continuación, eliminamos el elemento en\((2,0)\) (círculo verde). Para ello, restamos, de esta fila, un múltiplo de fila\(0\). El factor a utilizar es\(2/1=2\), que es el elemento en\((2,0)\) dividido por el elemento\((0,0)\) (diagonal):
\[(2x_0 + 6x_1 + 2x_2) - (2/1)(1x_0 + 2x_1 + 3x_2) = 4 - (2/1) 3\]
El resultado es

A continuación, eliminamos el\((2,1)\) elemento (círculo azul). Este elemento se encuentra en columna\(1\), por lo que lo eliminamos restando un múltiplo de fila\(1\). El factor a utilizar es\(2/(-4)=-0.5\), que es el\((2,1)\) elemento dividido por el elemento\((1,1)\) (diagonal):
\[(0x_0 + 2x_1 - 4x_2) - (2/(-4))(0x_0 - 4x_1 - 7x_2) = -5 - (2/(-4)) (-2)\]
El resultado es
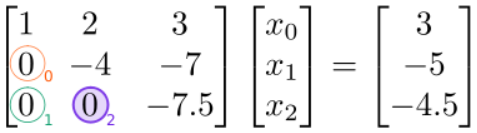
Ya hemos completado la fase de reducción de filas, ya que la matriz del lado izquierdo es superior-triangular (es decir, todas las entradas por debajo de la diagonal se han establecido en cero).
5.1.2 Sustitución por retroceso
En la fase de sustitución por retroceso, leemos la solución desde la fila más inferior hasta la fila más alta. Primero, examinamos la fila inferior:

Gracias a la reducción de filas, todos los elementos de la matriz en esta fila son cero excepto el último. De ahí que podamos leer la solución
\[x_{2}=(-4.5)/(-7.5)=0.6.\]
A continuación, nos fijamos en la fila de arriba:
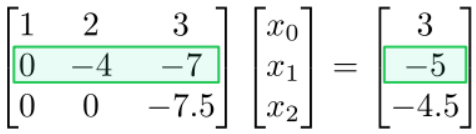
Esta es una ecuación que involucra\(x_{1}\) y\(x_{2}\). Pero a partir del paso anterior de retro-sustitución, lo sabemos\(x_{2}\). Por lo tanto, podemos resolver para
\[x_1 = [-5 - (-7) (0.6)] / (-4) = 0.2.\]
Por último, nos fijamos en la fila de arriba:

Esto involucra las tres variables\(x_{0}\),\(x_{1}\), y\(x_{2}\). Pero ya sabemos\(x_{1}\) y\(x_{2}\), así podemos leer la solución para\(x_{0}\). El resultado final es
\[\begin{bmatrix}x_0 \\ x_1 \\ x_2\end{bmatrix} = \begin{bmatrix}0.8 \\ 0.2 \\ 0.6\end{bmatrix}.\]
5.1.3 Tiempo de ejecución
Resumamos los componentes del algoritmo de eliminación gaussiana y analicemos cuántos pasos toma cada parte:
| Reducción de filas | ||||
|---|---|---|---|---|
| • | Paso adelante a través de las filas. Para cada fila\(n\), | \(N\)pasos | ||
| • | Realizar pivotamiento (que se discutirá más adelante). | \(N-n +1 \sim N\)pasos | ||
| • | Paso adelante a través de las filas más grandes que\(n\). Para cada una de esas filas\(m\), | \(N-n \sim N\)pasos | ||
| • | Restar los\((A'_{mn}/A'_{nn})\) tiempos\(n\) de fila de la fila\(m\) (donde\(\mathbf{A}'\) está la matriz actual). Esto elimina el elemento de la matriz en\((m,n)\). | \(O(N)\)operaciones aritméticas | ||
| Sustitución por retroceso | ||||
| • | Paso hacia atrás a través de las filas. Para cada fila\(n\), | \(N\)pasos | ||
| • | Sustituto en las soluciones\(x_{m}\) para\(m>n\) (que ya se encuentran). De ahí, encuentra\(x_{n}\). | \(N-n \sim O(N)\)operaciones aritméticas | ||
(El procedimiento de “pivotar” aún no se ha discutido; lo haremos en una sección posterior).
Se concluye que el tiempo de ejecución de la fase de reducción de fila se escala como\(O(N^{3})\), y el tiempo de ejecución de la fase de retrosustitución se escala como\(O(N^{2})\). Por lo tanto, el tiempo de ejecución general del algoritmo escala como\(O(N^{3})\).


