10.4: Método Adams-Moulton
- Page ID
- 125112
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
En el método Adams-Moulton (AM2) de segundo orden, tomamos
\[\vec{y}_{n+1} = \vec{y}_n + \frac{h}{2}\left[ \vec{F}(\vec{y}_{n}, t_{n}) + \vec{F}(\vec{y}_{n+1}, t_{n+1})\right].\]
Conceptualmente, el término derivado aquí es el promedio de los términos derivados Adelante Euler y Atrás Euler. Porque\(\vec{y}_{n+1}\) aparece en el lado derecho, este es un método implícito. Así, al igual que el Método de Euler hacia atrás, normalmente tiene que resolverse iterativamente, pero es numéricamente estable. La ventaja del método AM2 es que su error de truncamiento local es sustancialmente menor. Para ver esto, tomemos la derivada de ambos lados de la ODE en un paso de tiempo:
\[\int_{t_n}^{t_{n+1}} \frac{d\vec{y}}{dt} \; dt = \int_{t_n}^{t_{n+1}} \vec{F}(\vec{y}(t), t) \; dt\]
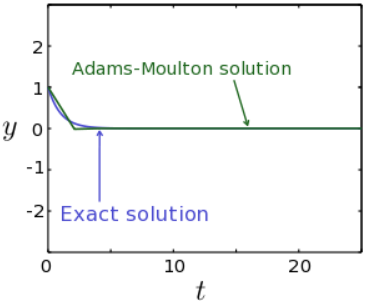
La integral en el lado izquierdo se reduce a\(\vec{y}_{n+1} - \vec{y}_n\). En cuanto a la integral en el lado derecho, si realizamos esta integral numéricamente usando la regla del trapecio, entonces el resultado es el término derivado en la fórmula AM2. El error de truncamiento local viene dado por el error numérico de la regla del trapecio, que es\(O(h^{3})\). Eso es una mejora de un orden en comparación con los métodos de Euler. (Con base en este argumento, también podemos ver que el método Forward Euler y los métodos Atrás Euler implican aproximar la integral en el lado derecho usando un área rectangular, con la altura dada por el valor at\(t_{n}\) y\(t_{n+1}\) respectivamente. A partir de esto, queda claro por qué el esquema AM2 da mejores resultados.)
También hay métodos Adams-Moulton de orden superior, que generan resultados aún más precisos al muestrear también la función derivada en pasos anteriores:\(F(\vec{y}_{n-1},t_{n-1})\)\(F(\vec{y}_{n-2},t_{n-2})\),, etc.
En la Fig. \(\PageIndex{1}\), trazamos la solución AM2 para el problema\(dy/dt = -\kappa y(t)\), utilizando los mismos parámetros (incluyendo el mismo tamaño de paso\(h\)) que en la Fig. 10.2.1 (Método Euler hacia adelante) y en la Fig. 10.3.1 (Método Euler hacia atrás). Es claro que los resultados de AM2 son significativamente más precisos.


