5.3: Solución general para el oscilador armónico amortiguado

Por ahora, supongamos\(\omega_0 \ne \gamma\). En la sección anterior, encontramos dos clases de soluciones específicas, con frecuencias complejas\(\omega_+\) y\(\omega_-\):\[z_+(t) = e^{-i\omega_+ t} \;\;\mathrm{and}\;\; z_-(t) = e^{-i\omega_- t}, \;\;\mathrm{where} \;\;\; \omega_\pm = -i\gamma \pm \sqrt{\omega_0^2 - \gamma^2}.\] Una solución general se puede encontrar construyendo una superposición lineal de estas soluciones:\[\begin{align} z(t) &= \psi_+ e^{-i\omega_+ t} + \psi_- e^{-i\omega_- t} \\ &= \psi_+ \, \exp\left[\left(-\gamma - i \sqrt{\omega_0^2 - \gamma^2}\right)t\right] \; +\; \psi_- \, \exp\left[\left(-\gamma +i\sqrt{\omega_0^2 - \gamma^2}\right)t\right]. \label{gensol}\end{align}\] Esta contiene dos parámetros complejos indeterminados, \(\psi_+\)y\(\psi_-\). Se trata de parámetros independientes ya que son coeficientes que multiplican diferentes funciones (las funciones son diferentes porque\(\omega_0 \ne \gamma\) implica eso\(\omega_+ \ne \omega_-\)).

Para obtener la solución general a la ecuación real del oscilador armónico amortiguado, debemos tomar la parte real de la solución compleja. El resultado puede simplificarse aún más dependiendo de si\(\omega_0^2 - \gamma^2\) es positivo o negativo. Esto conduce a soluciones poco amortiguadas o soluciones sobreamortiguadas, como se discute en las siguientes subsecciones.

¿Y si\(\omega_0 = \gamma\)? En esta instancia,\(\omega_+ = \omega_-\), lo que significa que\(\psi_+\) y\(\psi_-\) no son parámetros independientes. Por lo tanto, ¡la ecuación anterior para\(z(t)\) no es una solución general válida! Discutiremos cómo manejar este caso Sección 5.3.

Movimiento poco amortiguado

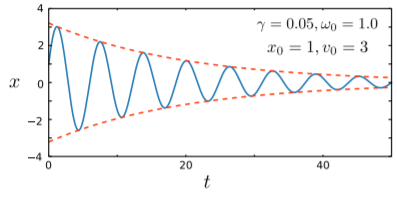
Para\(\omega_0 > \gamma\), definamos, por conveniencia,\[\Omega = \sqrt{\omega_0^2 - \gamma^2}.\] Entonces podemos simplificar la solución real de la siguiente manera:\[\begin{align} x(t) &= \mathrm{Re}\left[z(t)\right] \\ &= e^{-\gamma t} \; \mathrm{Re}\left[\psi_+ \, e^{-i \Omega t} \,+\, \psi_- \, e^{i\Omega t}\right] \\ &= e^{-\gamma t} \left[ A\cos\left(\Omega t\right) + B \sin\left(\Omega t\right)\right], \;\;\mathrm{where}\;\; A, B \in \mathbb{R} \label{underdamped-sol}\end{align}\] Con un poco de álgebra, podemos demostrar que\[A = \mathrm{Re}\left[\psi_+ + \psi_-\right], \quad B = \mathrm{Im}\left[\psi_+ - \psi_-\right].\] Esto se llama una solución poco amortiguada. Los coeficientes\(A\) y\(B\) actúan como dos parámetros reales independientes, por lo que esta es una solución general válida para la ecuación real del oscilador armónico amortiguado. Usando las fórmulas trigonométricas, la solución puede escribirse de manera equivalente como\[x(t) = C e^{-\gamma t} \cos\left[\Omega t + \Phi\right],\] con los parámetros\(C = \sqrt{A^2 + B^2}\) y\(\Phi = - \tan^{-1}\left[B/A\right]\).

Como se muestra a continuación, la trayectoria es una oscilación cuya amplitud disminuye con el tiempo. La disminución en la amplitud se puede visualizar utilizando una “envolvente” suave dada por\(\pm C e^{-\gamma t}\), que se dibuja con guiones en la figura. Dentro de esta envolvente, la trayectoria oscila con la frecuencia\(\Omega = \sqrt{\omega_0^2 - \gamma^2}\), que es ligeramente menor que la frecuencia natural de oscilación\(\omega_0\).

Figura\(\PageIndex{1}\)

Movimiento sobre-amortiguado

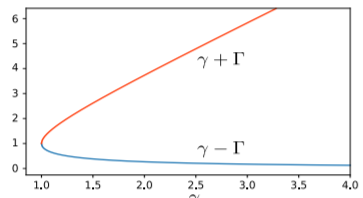
Porque\(\omega_0 < \gamma\), el término raíz cuadrada es imaginario. Es conveniente definir\[\Gamma = \sqrt{\gamma^2 - \omega_0^2} \quad \Rightarrow \quad \sqrt{\omega_0^2 - \gamma^2} = i \Gamma.\] Entonces la solución real se simplifica de una manera diferente:\[\begin{align} x(t) = \mathrm{Re}\left[z(t)\right] &= \mathrm{Re}\left[\psi_+ e^{\left(-\gamma + \Gamma\right)t} + \psi_- e^{\left(-\gamma - \Gamma\right)t} \right] \\ &= C_+ e^{-(\gamma - \Gamma) t} + C_- e^{-(\gamma + \Gamma) t}, \label{overdamped-sol}\end{align}\] donde A\[C_\pm = \mathrm{Re}[\psi_\pm].\] esto se le llama una solución sobreamortiguada. Consiste en dos términos, ambos en descomposición exponencial en el tiempo, con\((\gamma-\Gamma)\) y\((\gamma + \Gamma)\) sirviendo como las tasas de decaimiento. Nótese que ambas tasas de decaimiento son números reales positivos, porque\(\Gamma < \gamma\) a partir de la definición de\(\Gamma\). Además, tenga en cuenta que\((\gamma - \Gamma)\) disminuye con\(\gamma\), mientras que\((\gamma + \Gamma)\) aumenta con\(\gamma\), como se muestra a continuación:

Figura\(\PageIndex{2}\)

La siguiente gráfica muestra la trayectoria del oscilador sobreamortiguado:

Figura\(\PageIndex{3}\)

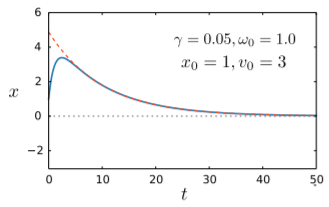
Los guiones rojos muestran la curva limitante determinada por la tasa de decaimiento\((\gamma - \Gamma)\). La otra tasa de decaimiento\((\gamma + \Gamma)\),, corresponde a un exponencial de descomposición más rápida, por lo que en tiempos largos el segundo término en la Ec. \(\eqref{overdamped-sol}\)se vuelve insignificante en comparación con el primer término. Entonces la solución se acerca al límite\[x(t) \approx C_+ e^{-(\gamma - \Gamma) t} \qquad (\mathrm{for}~\mathrm{large}~t). \label{overdamped-long-t}\] Curiosamente, ya que\((\gamma-\Gamma)\) es una función decreciente de\(\gamma\), cuanto más fuerte es la amortiguación, más lenta es la tasa de decaimiento en tiempos largos. ¡Esto es lo contrario de lo que sucede en el régimen subamortiguado!

¿Por qué sucede esto? En el régimen sobreamortiguado, el movimiento del oscilador está dominado por la fuerza de amortiguación más que por la fuerza del resorte; a medida que el oscilador intenta regresar a su posición de equilibrio\(x = 0\), la amortiguación actúa contra este movimiento. De ahí que cuanto más fuerte sea la amortiguación, más lenta será la decadencia al equilibrio. Esto contrasta bruscamente con la Sección 5.3, donde la fuerza del resorte domina la fuerza de amortiguación. En ese caso, una amortiguación más fuerte acelera la decadencia al equilibrio, al hacer que la energía cinética de la oscilación se disipe más rápidamente.

Amortiguación crítica

La amortiguación crítica ocurre cuando\(\omega_0 = \gamma\). Bajo esta condición especial, la Ec. \(\eqref{gensol}\)reduce a\[z(t) = \left(\psi_+ + \psi_-\right) e^{-\gamma t}.\] Esto tiene solo un parámetro complejo independiente, es decir, el parámetro\((\psi_+ + \psi_-)\). Por lo tanto, no puede ser una solución general para la ecuación del oscilador armónico amortiguado complejo, que sigue siendo una ODE de segundo orden.

No entraremos en detalles aquí respecto al procedimiento para encontrar la solución general para el oscilador amortiguado críticamente, dejándolo como una Sección 5.5 para el lector interesado. Básicamente, el procedimiento consiste en que Taylor expanda la solución a ambos lados del punto crítico, y luego mostrar que existe una solución de la forma\[z(t) = \left(A + B t\right)\, e^{-\gamma t}, \label{critical-sol}\] que contiene los dos parámetros independientes deseados.

La solución amortiguada críticamente contiene una constante de decaimiento exponencial de\(\gamma\), que es la misma que la constante de decaimiento para la función envolvente en el régimen subamortiguado [Ec. \(\eqref{underdamped-sol}\)], y menores que las constantes de decaimiento a largo plazo en el régimen sobreamortiguado [Ec. \(\eqref{overdamped-long-t}\)]. Por lo tanto, podemos considerar la solución amortiguada críticamente como la solución no oscilatoria de descomposición más rápida.

Esta característica de amortiguación crítica se emplea en muchos contextos de ingeniería, siendo el más familiar los cierras automáticos de puertas. Si la amortiguación es demasiado débil o la fuerza del resorte es demasiado fuerte (amortiguada), la puerta se cerrará de golpe, mientras que si la amortiguación es demasiado fuerte o la fuerza del resorte es demasiado débil (amortiguación inferior), la puerta tarda innecesariamente en cerrarse. De ahí que los cierras de puerta se ajusten a un “punto dulce” correspondiente al punto crítico de amortiguación.