7.1: Continuidad y Diferenciabilidad Complejas
- Page ID
- 125901
El concepto de función compleja continua hace uso de una “definición épsilon-delta”, similar a la definición de funciones de variables reales (ver Capítulo 1):
Definición: Word
Una función compleja\(f(z)\) es continua en\(z_0 \in \mathbb{C}\) si, para alguna\(\epsilon > 0\), podemos encontrar una\(\delta > 0\) tal que\[\big|\, z - z_0 \,\big| < \delta \;\;\; \Rightarrow \;\;\; \big|\, f(z) - f(z_0) \,\big| < \epsilon.\]
Aquí,\(\big|\cdots\big|\) denota la magnitud de un número complejo. Si tienes dificultad para procesar esta definición, no te preocupes; básicamente dice que como\(z\) se varía sin problemas, no hay saltos abruptos en el valor de\(f(z)\).
Si una función es continua en un punto\(z\), podemos definir su derivada compleja como\[f'(z) = \frac{df}{dz} = \lim_{\delta z\rightarrow 0} \frac{f(z+\delta z) - f(z)}{\delta z}.\] Esta es muy similar a la definición de la derivada para una función de una variable real (ver Capítulo 1). Sin embargo, hay una complicación que no aparece en el caso real: el infinitesimal\(\delta z\) es un número complejo, no sólo un número real, sin embargo, la definición anterior no especifica el argumento de\(\delta z\). La elección del argumento de\(\delta z\) es equivalente a la dirección en el plano complejo en el que\(\delta z\) apunta, como se muestra en la siguiente figura:
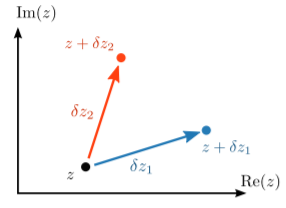
En principio, podríamos obtener resultados diferentes de la fórmula anterior cuando conectamos diferentes infinitesimales\(\delta z\), incluso en el límite donde\(\delta z \rightarrow 0\) y aunque\(f(z)\) sea continuo.
Ejemplo\(\PageIndex{1}\)
Considera la función\(f(z) = z^*\). Según la fórmula para el derivado complejo,\[\lim_{\delta z \rightarrow0} \frac{f(z+\delta z) - f(z)}{\delta z} = \lim_{\delta z \rightarrow0} \frac{z^*+\delta z^* - z^*}{\delta z} = \lim_{\delta z \rightarrow0} \frac{\delta z^*}{\delta z}.\] Pero si enchufamos un real\(\delta z\), obtenemos un resultado diferente al de enchufar un imaginario\(\delta z\):\[\begin{align} \delta z \in \mathbb{R} \;\; &\Rightarrow \frac{\delta z^*}{\delta z} = 1.\\ \delta z \in i \cdot \mathbb{R} &\Rightarrow \frac{\delta z^*}{\delta z} = -1.\end{align}\]
Podemos lidiar con esta complicación considerando la derivada compleja como bien definida solo si la definición anterior da la misma respuesta independientemente del argumento de\(\delta z\). Si una función satisface esta propiedad en un punto\(z\), decimos que la función es complejo-diferenciable en\(z\).
El ejemplo anterior mostró que no\(f(z) = z^*\) es complejo-diferenciable para ninguno\(z \in \mathbb{C}\). Por otro lado, el siguiente ejemplo muestra que la función\(f(z) = z\) es complejo-diferenciable para todos\(z \in \mathbb{C}\):
Ejemplo\(\PageIndex{2}\)
La función\(f(z) = z\) es compleja diferenciable para cualquiera\(z \in \mathbb{C}\), ya que\[\lim_{\delta z \rightarrow0} \frac{f(z+\delta z) - f(z)}{\delta z} = \lim_{\delta z \rightarrow0} \frac{z+\delta z - z}{\delta z} = \lim_{\delta z \rightarrow0} \frac{\delta z}{\delta z} = 1.\] La razón por la que el resultado no depende del argumento de\(\delta z\) es que la fórmula derivada simplifica a la fracción\(\delta z / \delta z\), que es igual a 1 para cualquier \(|\delta z| > 0\). Tenga en cuenta que simplificamos la fracción a 1 antes de tomar el límite\(\delta z \rightarrow 0\). No podemos tomar primero el límite, porque no\(0/0\) está definido.


