8.1: Potencias no enteras como operaciones de múltiples valores

Dado un número complejo en su representación polar,\(z = r\exp[i\theta]\), elevándose al poder de\(p\) podría manejarse de esta manera:\[z^p = \left(re^{i\theta}\right)^p = r^p e^{ip\theta}.\] Echemos un vistazo más de cerca al complejo término exponencial\(e^{ip\theta}\). Ya que\(\theta = \mathrm{arg}(z)\) es un ángulo, podemos cambiarlo por cualquier entero múltiplo de\(2\pi\) sin alterar el valor de\(z\). Teniendo en cuenta este hecho, podemos reescribir la ecuación anterior con más cuidado como\[z^p = \left(r\,e^{i(\theta + 2\pi n)}\right)^p = \left(r^p e^{ip\theta} \right) e^{2\pi i n p} \quad\; \mathrm{where}\;\; n\in\mathbb{Z}.\] Así, hay un factor ambiguo de\(\exp(2\pi i n p)\), donde\(n\) está cualquier entero. Si\(p\) es un entero, no hay problema, ya que\(2\pi n p\) será un entero múltiplo de\(2\pi\), por lo que\(z^p\) tiene el mismo valor independientemente de\(n\):\[z^p = r^p e^{ip\theta} \;\;\textrm{unambiguously} \;\;\;(\text{if}\,p\in\mathbb{Z}).\] Pero si no\(p\) es un entero, hay no es una respuesta única, ya que\(\exp\left(2 \pi i np\right)\) tiene valores diferentes para diferentes\(n\). En ese caso, “subir al poder de\(p\)” es una operación multivalorada. No puede tratarse como una función en el sentido habitual, ya que las funciones deben tener salidas inequívocas (ver Capítulo 0).

Raíces de la unidad

Echemos un vistazo más de cerca al término exponencial problemático,\[\exp\left(2\pi i np\right), \quad n \in \mathbb{Z}.\] Si\(p\) es irracional,\(2\pi np\) nunca se repite módulo\(2\pi\). Así,\(z^p\) tiene un conjunto infinito de valores, uno por cada entero\(n\).

Más interesante es el caso de un poder racional no entero, que se puede escribir como\(p = P/Q\) donde\(P\) y\(Q\) son enteros sin divisor común. Se puede probar usando aritmética modular (aunque no entraremos en los detalles) que\(2\pi n\, (P/Q)\) tiene exactamente valores\(Q\) únicos módulo\(2\pi\):\[2\pi n\, \left(\frac{P}{Q}\right) = 2\pi \times \left\{0,\, \frac{1}{Q},\, \frac{2}{Q},\, \dots, \frac{(Q-1)}{Q} \right\} \quad(\mathrm{modulo} \; 2\pi).\] Este conjunto de valores es independiente del numerador\(P\), que simplemente afecta a la secuencia en la que se generan los números. Podemos aclarar esto usando algunos ejemplos simples:

Ejemplo\(\PageIndex{1}\)

Considere la compleja operación de raíz cuadrada,\(z^{1/2}\). Si escribimos\(z\) en su respresentación polar,\[z = r e^{i\theta},\] entonces\[z^{1/2} = \left[r \, e^{i(\theta + 2 \pi n)} \right]^{1/2} = r^{1/2} \, e^{i\theta/2} \, e^{i \pi n}, \quad n \in \mathbb{Z}.\] El factor de\(e^{i\pi n}\) tiene dos valores posibles:\(+1\) para par\(n\), y\(-1\) para impar\(n\). Por lo tanto,\[z^{1/2} = r^{1/2} \, e^{i\theta/2} \;\times\; \left\{1, -1\right\}.\]

Ejemplo\(\PageIndex{2}\)

Considera la operación de raíz cubo\(z^{1/3}\). Nuevamente, escribimos\(z\) en su representación polar, y obtenemos\[z^{1/3} = r^{1/3} \, e^{i\theta/3} \, e^{2\pi i n/3}, \quad n \in \mathbb{Z}.\] El factor de\(\exp(2\pi i n/3)\) tiene los siguientes valores para diferentes\(n\):\[\nonumber\begin{array}{|c||c|c|c|c|c|c|c|c|c|} \hline n &\cdots & -2 & -1 & 0 & 1 & 2 & 3 & 4 & \cdots \\ \hline e^{2\pi i n/3} &\cdots & e^{2\pi i /3} & e^{-2\pi i /3} & \;\,\;1\;\,\; & e^{2\pi i /3} & e^{-2\pi i /3} & \;\,\;1\;\,\; & e^{2\pi i /3} & \cdots \\ \hline \end{array}\] A partir del patrón, vemos que hay tres valores posibles del factor exponencial:\[e^{2\pi i n/3} = \left\{1, e^{2\pi i /3}, e^{-2\pi i /3}\right\}.\] Por lo tanto, la operación de raíz cubo tiene tres valores distintos:\[z^{1/3} = r^{1/3} \, e^{i\theta/3} \;\times\; \left\{1, e^{2\pi i /3}, e^{-2\pi i /3}\right\}.\]

Ejemplo\(\PageIndex{3}\)

Considera la operación\(z^{2/3}\). Nuevamente, escribiendo\(z\) en su representación polar,\[z^{2/3} = r^{2/3} \, e^{2i\theta/3} \, e^{4\pi i n/3}, \quad n \in \mathbb{Z}.\] El factor de\(\exp(4\pi i n/3)\) tiene los siguientes valores para diferentes\(n\):\[\nonumber\begin{array}{|c||c|c|c|c|c|c|c|c|c|} \hline n &\cdots & -2 & -1 & 0 & 1 & 2 & 3 & 4 & \cdots \\ \hline e^{4\pi i n/3} &\cdots & e^{-2\pi i /3} & e^{2\pi i /3} & \;\,\;1\;\,\; & e^{-2\pi i /3} & e^{2\pi i /3} & \;\,\;1\;\,\; & e^{-2\pi i /3} & \cdots \\ \hline \end{array}\] De ahí, hay tres valores posibles de este factor exponencial,\[e^{2\pi i n (2/3)} = \left\{1, e^{2\pi i /3}, e^{-2\pi i /3}\right\}.\] Tenga en cuenta que este es exactamente el mismo conjunto que obtenido para\(e^{2\pi i n/3}\) en el ejemplo anterior, de acuerdo con la afirmación anterior de que el numerador no\(P\) tiene efecto sobre el conjunto de valores. Por lo tanto,\[z^{2/3} = r^{2/3} \, e^{2i\theta/3} \;\times\; \left\{1, e^{2\pi i /3}, e^{-2\pi i /3}\right\}.\]

De los ejemplos anteriores, deducimos la siguiente expresión para los poderes racionales:\[z^{P/Q} = r^{P/Q} \; e^{i\theta\, (P/Q)}\, \times \left\{1,\, e^{2\pi i \cdot (1/Q)},\, e^{2\pi i \cdot (2/Q)},\, \dots, e^{2\pi i \cdot [(1-Q)/Q]} \right\}.\] Las cantidades entre los corchetes se llaman las raíces de la unidad. En el plano complejo, se asientan en puntos\(Q\) espaciados uniformemente en el círculo unitario, con\(1\) como uno de los valores:

Figura\(\PageIndex{1}\)

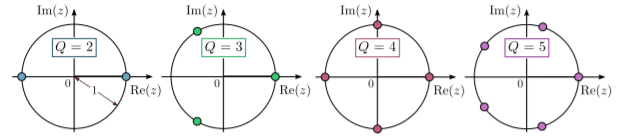
Logaritmos complejos

Aquí hay otra forma de pensar sobre los poderes no enteros. Recordemos lo que significa elevar un número a, digamos, la potencia de 5: simplemente multiplicamos el número por sí mismo cinco veces. ¿Qué pasa con elevar un número a una potencia no entera\(p\)? Para el caso real, se utilizó la siguiente definición basada en una combinación de funciones exponenciales y logaritmos:\[x^p \equiv \exp\,\left[\,p\ln(x)\right].\] Esta definición se basa en el hecho de que, para entradas reales, el logaritmo es una función bien definida. Eso, a su vez, viene de la definición del logaritmo como el inverso de la función exponencial. Dado que el exponencial real es uno a uno, su inverso también es uno a uno.

El exponencial complejo, sin embargo, es de muchos a uno, ya que cambiar su entrada por cualquier múltiplo de\(2\pi i\) produce la misma salida:\[\exp(z + 2\pi i n) = \exp(z) \cdot e^{2\pi i n} = \exp(z) \quad \forall\; n \in \mathbb{Z}.\] La inversa del exponencial complejo es el logaritmo complejo. Dado que el exponencial complejo es de muchos a uno, el logaritmo complejo no tiene una salida única. En cambio,\(\ln(z)\) se refiere a un conjunto discreto infinito de valores, separados por múltiplos enteros de\(2\pi i\). Podemos expresar este estado de cosas de la siguiente manera:\[\ln(z) = \big[\ln(z)\big]_{\mathrm{p.v.}}\; +\; 2 \pi i n, \quad n \in \mathbb{Z}. \label{logformula}\] Aquí,\([\ln(z)]_{\mathrm{p.v.}}\) denota el valor principal de\(\ln(z)\), que se refiere a un valor de referencia de la operación logaritmo (que definiremos más adelante). ¡No pienses en el valor principal como el resultado “real” de la\(\ln(z)\) operación! Existen múltiples valores, cada uno igualmente legítimo; el valor principal no es más que uno de estos posibles resultados.

Taponamiento Eq. \(\eqref{logformula}\)en la fórmula\(z^p \equiv \exp\left[p\ln(z)\right]\) da\[\begin{align} z^p &= \exp\Big\{p\big([\ln(z)]_{\mathrm{p.v.}} + 2\pi i n\big)\Big\}\\ &= \exp\Big\{p[\ln(z)]_{\mathrm{p.v.}}\Big\} \times e^{2\pi i np}, \quad n \in \mathbb{Z}.\end{align}\] El factor final, que es responsable del multivalor, son las raíces de la unidad que se encuentran en la Sección 8.1.