8.2: Sucursales

Se han discutido dos ejemplos de operaciones complejas multivaloradas: las potencias no enteras y el logaritmo complejo. Sin embargo, generalmente preferimos tratar con funciones en lugar de operaciones de múltiples valores. Uno de los principales factores motivadores es que el concepto de derivado complejo se formuló en términos de funciones, no operaciones multivalorizadas.

Existe un procedimiento estándar para convertir operaciones multivaloradas en funciones. Primero, definimos una o más curvas en el plano complejo, llamadas cortes de rama (la razón de este nombre se explicará más adelante). A continuación, modificamos el dominio (es decir, el conjunto de entradas permisibles) excluyendo todos los valores de\(z\) mentir sobre un corte de rama. Entonces las salidas de la operación multivalorada pueden agruparse en ramas discretas, con cada rama comportándose como una función.

El procedimiento anterior se puede entender a través del ejemplo de la raíz cuadrada.

Ramas de la raíz cuadrada compleja

Como vimos en la Sección 8.1, la raíz cuadrada compleja,\(z^{1/2}\), tiene dos valores posibles. Podemos definir las dos ramas de la siguiente manera:

1. Define un corte de rama a lo largo del eje real negativo, de modo que el dominio excluya todos los valores\(z\) a lo largo del corte de rama. En otras palabras, solo consideraremos números complejos cuya representación polar pueda escribirse como\[z = r e^{i\theta}, \quad \theta \in (-\pi, \pi).\] (Para aquellos que no estén familiarizados con esta notación,\(\theta \in (-\pi, \pi)\) se refiere al intervalo\(-\pi < \theta < \pi\). Los paréntesis indican que los valores límite de\(-\pi\) y\(\pi\) están excluidos. Por el contrario, escribiríamos\(\theta \in [-\pi, \pi]\) para referirnos al intervalo\(-\pi \le \theta \le \pi\), con los corchetes indicando que se incluyen los valores límite.)

2. Una rama está asociada con la\(+1\) raíz. En esta rama, para\(z = re^{i\theta}\), el valor es\[f_+(z) = r^{1/2} \, e^{i\theta/2}, \quad \theta \in (-\pi, \pi).\]

3. La otra rama está asociada con la raíz de la unidad\(-1\). En esta rama, el valor es\[f_-(z) = -r^{1/2} \, e^{i\theta/2}, \quad \theta \in (-\pi, \pi).\]

En la siguiente gráfica, se puede observar cómo la variación\(z\) afecta las posiciones de\(f_+(z)\) y\(f_-(z)\) en el plano complejo:

Figura\(\PageIndex{1}\)

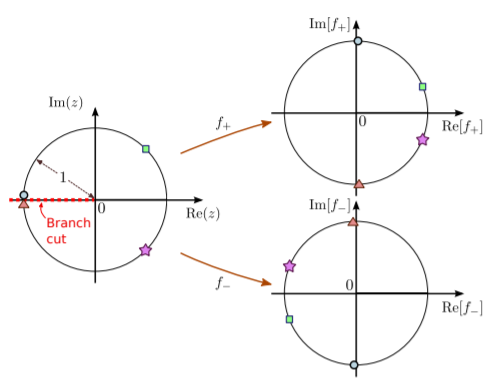
La línea discontinua roja en la gráfica izquierda indica el corte de rama. Nuestras definiciones de\(f_+(z)\) e\(f_-(z)\) implícitamente dependen de la elección de colocar el corte de rama sobre el eje real negativo, lo que llevó a la representación del argumento de\(z\) as\(\theta \in (-\pi,\pi)\).

En la figura anterior, tenga en cuenta que\(f_+(z)\) siempre se encuentra en la mitad derecha del plano complejo, mientras que\(f_-(z)\) se encuentra en la mitad izquierda del plano complejo. Ambos\(f_+\) y\(f_-\) son funciones bien definidas con salidas inequívocas, aunque con dominios que no cubren todo el plano complejo. Además, son analíticos sobre todo su dominio (es decir, todo el plano complejo excepto el corte de rama); esto se puede probar usando las ecuaciones de Cauchy-Riemann, y se deja como ejercicio.

El punto final del corte de rama se denomina punto de ramificación. Para\(z = 0\), ambas ramas dan el mismo resultado:\(f_+(0) = f_-(0) = 0\). Tendremos más que decir sobre los puntos de sucursal en la Sección 8.2.

Diferentes cortes de rama para la raíz cuadrada compleja

En el ejemplo anterior, tal vez se esté preguntando por qué el corte de rama tiene que estar a lo largo del eje real negativo. De hecho, esta elección no es única. Por ejemplo, podríamos colocar el corte de rama a lo largo del eje real positivo. Esto corresponde a especificar la entrada\(z\) usando un intervalo diferente para\(\theta\):\[z = re^{i\theta}, \quad \theta \in (0, 2\pi).\] A continuación, usamos las mismas fórmulas que antes para definir las ramas de la raíz cuadrada compleja:\[f_\pm(z) = \pm r^{1/2} \, e^{i\theta/2}.\] Pero debido a que el dominio de\(\theta\) ha sido cambiado a \((0, 2\pi)\), el conjunto de entradas\(z\) ahora excluye el eje real positivo. Con esta nueva opción de corte de rama, las ramas se muestran en la siguiente figura.

Figura\(\PageIndex{2}\)

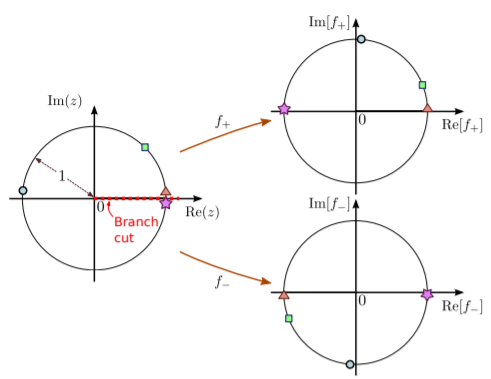
Estas dos funciones de rama son distintas a las que teníamos antes. Ahora, siempre\(f_+(z)\) está en la mitad superior del plano complejo, y\(f_-(z)\) en la mitad inferior del plano complejo. Sin embargo, ambas ramas siguen teniendo el mismo valor en el punto de bifurcacion:\(f_+(0) = f_-(0) = 0\).

El corte de rama sirve como límite donde dos ramas se “pegan” entre sí. Se puede pensar en “cruzar” un corte de rama como tener el efecto de moverse continuamente de una rama a otra. En la figura anterior, considera el caso donde\(z\) está justo por encima del corte de rama. Entonces\(f_+(z)\) yace justo por encima del eje real positivo, y\(f_-(z)\) se encuentra justo debajo del eje real negativo. A continuación, considere\(z\) acostarse justo debajo del corte de rama. Esto equivale a un pequeño desplazamiento hacia abajo de\(z\), “cruzando” el corte de rama. Para este caso,\(f_-(z)\) ahora se encuentra justo debajo del eje real positivo, cerca de donde\(f_+(z)\) estaba anteriormente. Además,\(f_+(z)\) ahora yace justo por encima del eje real negativo, cerca de donde\(f_-(z)\) estaba anteriormente. Al cruzar el corte de rama se intercambian los valores de las ramas positivas y negativas.

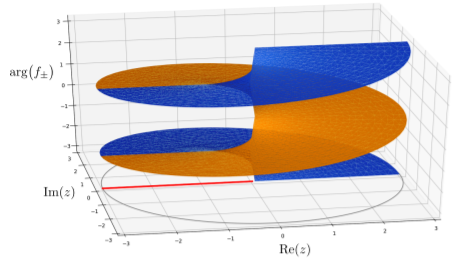
La gráfica tridimensional a continuación proporciona otra forma de visualizar el papel del corte de rama. Aquí, los ejes horizontales corresponden a\(\mathrm{Re}(z)\) y\(\mathrm{Im}(z)\). El eje vertical muestra los argumentos para los dos valores de la raíz cuadrada compleja, con\(\mathrm{arg}\big[f_+(z)\big]\) trazados en naranja y\(\mathrm{arg}\big[f_-(z)\big]\) trazados en azul. Si variamos la elección del corte de rama, eso simplemente afecta qué valores de la operación multivalorada se asignan a la rama\(+\) (naranja), y qué valores se asignan a la rama\(-\) (azul). De ahí que la elección del corte de rama sea solo una elección sobre cómo dividir las ramas de una operación multivalorada.

Figura\(\PageIndex{3}\)

Puntos de sucursal

La punta de cada corte de rama se llama punto de ramificación. Un punto de ramificación es un punto donde la operación multivalorada da una respuesta inequívoca, con diferentes ramas dando la misma salida. Mientras que la elección de los cortes de rama no es única, las posiciones de los puntos de ramificación de una operación multivalorada se determinan de manera única.

Para los fines de este curso, en su mayoría solo es necesario recordar los puntos de sucursal para dos casos comunes:

• La\(z^p\) operación (para no enteros\(p\)) tiene puntos de ramificación en\(z = 0\) y\(z = \infty\). Para los poderes racionales\(p = P/Q\), donde\(P\) y no\(Q\) tienen divisor común, hay\(Q\) ramas, una por cada raíz de unidad. En cada punto de sucursal, todas las\(Q\) sucursales se encuentran.

• El logaritmo complejo tiene puntos de ramificación en\(z = 0\) y\(z = \infty\). Hay una serie infinita de ramas, separadas entre sí por múltiplos de\(2 \pi i\). En cada punto de sucursal, todas las sucursales se encuentran.

Podemos ver fácilmente que\(z^p\) debe tener un punto de rama en\(z = 0\): su único valor posible en el origen es\(0\), independientemente de qué raíz de unidad escojamos. Para entender los otros puntos de rama enumerados anteriormente, se requiere una comprensión más clara del concepto de “infinito” para números complejos, por lo que discutiremos eso ahora.