9.1: Integrales de contorno

Recordemos que para una función real\(f(x)\), la integral definida de\(x=a\) a\(x=b\) es el área bajo la curva entre esos dos puntos. Como se discute en el Capítulo 3, la integral se puede expresar como una expresión límite: dividimos el intervalo en\(N\) segmentos de ancho\(\Delta x\), tomamos la suma de\(\Delta x\, f(x_n)\), y vamos al\(N \rightarrow \infty\) límite:\[\int_a^b dx\; f(x) \;=\; \lim_{N \rightarrow 0} \, \sum_{n=0}^{N} \Delta x\; f(x_n), \;\;\;\mathrm{where}\;\;\;x_n = a + n\Delta x, \;\;\Delta x = \frac{b-a}{N}.\] Ahora supongamos \(f\)es una función compleja de una variable compleja. Una forma directa de definir la integral de\(f(z)\) es adoptar una expresión análoga:\[\lim_{N \rightarrow 0} \, \sum_{n=0}^{N} \Delta z\; f(z_n)\] Pero hay un inconveniente conceptual: dado que\(f\) toma entradas complejas, los valores de no\(z_n\) necesitan estar en la línea real. En general, los números complejos\(z_n\) forman un conjunto de puntos en el plano complejo. Para acomodar esto, podemos imaginar encadenar una secuencia de puntos\(z_1, z_2, \dots, z_N\), separados por desplazamientos\(\Delta z_1, \Delta z_2, \Delta z_3, \dots, \Delta z_{N-1}\):

Figura\(\PageIndex{1}\)

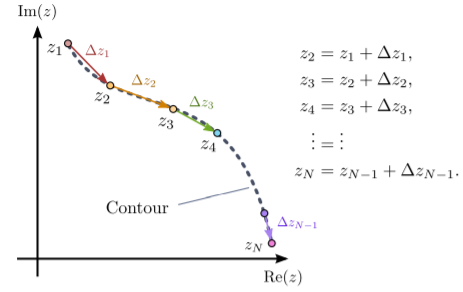
Entonces la suma que nos interesa es\[\sum_{n=1}^{N-1} \Delta z_n\; f(z_n) \;=\; \Delta z_1\, f(z_1) + \Delta z_2\, f(z_2) + \cdots + \Delta z_{N-1}\, f(z_{N-1}).\] En el límite\(N \rightarrow \infty\), cada desplazamiento\(\Delta z_{n}\) se vuelve infinitesimal, y la secuencia de puntos\(\{z_1, z_2, \dots, z_N\}\) se convierte en una trayectoria continua en el plano complejo (ver Sección 4.6). Tal trayectoria se llama contorno. Denotemos un contorno dado por un símbolo abstracto, como\(\Gamma\). Entonces la integral de contorno sobre\(\Gamma\) se define como\[\int_\Gamma \, f(z)\, dz = \lim_{N \rightarrow \infty} \sum_{n=1}^{N-1} \Delta z_n\; f(z_n).\] El símbolo\(\Gamma\) en el subíndice del signo integral indica que la integral tiene lugar sobre el contorno\(\Gamma\). Al definir una integral de contorno, siempre es necesario especificar sobre qué contorno nos estamos integrando. Esto es análogo a especificar los puntos finales del intervalo sobre los cuales realizar una integral real definida. En el caso complejo, la variable de integración\(z\) se encuentra en un plano bidimensional (el plano complejo), no en una línea; por lo tanto, no podemos simplemente especificar dos puntos finales, y debemos especificar un contorno completo.

Además, tenga en cuenta que al definir un contorno\(\Gamma\) debemos especificar no sólo una curva en el plano complejo, sino también la dirección a lo largo de la cual transitar la curva. Si nos integramos a lo largo de la misma curva en la dirección opuesta, el valor de la integral de contorno cambia el signo (esto es similar a intercambiar los puntos finales de una integral real definida).

Nota

Una integral de contorno generalmente no puede interpretarse como el área bajo una curva, de la manera en que una integral real definida puede ser interpretada. En particular, el contorno no debe interpretarse erróneamente la gráfica del integrand! Recuerde siempre que en una integral de contorno, tanto el\(f(z)\) integrando como la variable de integración\(z\) son números complejos.

Además, el concepto de integral indefinida no puede generalizarse útilmente al caso complejo.

Integral de contorno a lo largo de una curva paramétrica

Las integrales de contorno simples se pueden calcular parametrizando el contorno. Considera una integral de contorno\[\int_\Gamma \, dz \; f(z),\] donde\(f\) es una función compleja de una variable compleja y\(\Gamma\) es un contorno dado. Como se discute en la Sección 4.6, podemos describir una trayectoria en el plano complejo mediante una función compleja de una variable real,\(z(t)\):\[\Gamma \equiv \Big\{z(t) \;\Big|\; t_1 < t < t_2\Big\}, \quad \mathrm{where}\;\; t \in \mathbb{R}, \,z(t) \in \mathbb{C}.\] Los números reales\(t_1\) y\(t_2\) especificar dos números complejos,\(z(t_1)\) y \(z(t_2)\), que son los puntos finales del contorno. El resto del contorno consiste en los valores de\(z(t)\) entre esos puntos finales. Siempre que podamos parametrizar\(\Gamma\) de tal manera, el desplazamiento complejo\(dz\) en la integral de contorno se puede escribir como\[dz \rightarrow dt\, \frac{dz}{dt}.\] Entonces podemos expresar la integral de contorno\(\Gamma\) como una integral definida sobre\(t\): \[\int_\Gamma dz\; f(z) = \int_{t_1}^{t_2} \; dt\; \frac{dz}{dt}\, f\big(z(t)\big).\]Esto se puede calcular utilizando técnicas de integración estándar. En la siguiente sección se da un ejemplo sencillo.

Una integral de contorno sobre un arco circular

Usemos el método de parametrización del contorno para calcular la integral del contorno\[\int_{\Gamma[R, \theta_1,\theta_2]} dz\; z^n,\; n\in\mathbb{Z},\] donde la trayectoria\(\Gamma[R, \theta_1,\theta_2]\) consiste en un arco de radio en sentido antihorario\(R > 0\), desde el punto\(z_1 = R e^{i\theta_1}\) hasta el punto\(z_2 = R e^{i\theta_2}\), como se muestra en la figura abajo:

Figura\(\PageIndex{2}\)

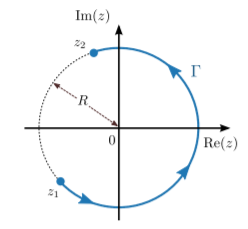
Podemos parametrizar el contorno de la siguiente manera:\[\Gamma[R, \theta_1,\theta_2] = \big\{z(\theta) \;\big|\; \theta_1 \le \theta \le \theta_2\big\}, \quad \mathrm{where}\;\, z(\theta) = R e^{i\theta}.\] Entonces la integral del contorno se puede convertir en una integral sobre el parámetro real\(\theta\):\[\begin{align} \int_{\Gamma[R, \theta_1,\theta_2]} dz\; z^n &= \int_{\theta_1}^{\theta_2} d\theta \; z^n \; \frac{dz}{d\theta} \\ &= \int_{\theta_1}^{\theta_2} d\theta \; \left( Re^{i\theta}\right)^n\, \left(iR\, e^{i\theta}\right) \\ &= i R^{n+1} \, \int_{\theta_1}^{\theta_2} d\theta \; e^{i(n+1)\theta}.\end{align}\] Para proceder, hay dos casos que debemos tratar por separado. Primero, para\(n \ne -1\),\[\int_{\theta_1}^{\theta_2} d\theta \; e^{i(n+1)\theta} = \left[\frac{e^{i(n+1)\theta}}{i(n+1)}\right]_{\theta_1}^{\theta_2} = \frac{e^{i(n+1)\theta_2} - e^{i(n+1)\theta_1}}{i(n+1)}.\] Segundo, tenemos el caso\(n = -1\). Esto no puede ser manejado por las ecuaciones anteriores, ya que el factor de\(n + 1\) en el denominador desaparecería. En cambio,\[\int_{\theta_1}^{\theta_2} d\theta \; \left[e^{i(n+1)\theta} \right]_{n=-1} \; = \int_{\theta_1}^{\theta_2} d\theta \;=\; \theta_2 - \theta_1.\] Armando los dos casos, llegamos al resultado\[\int_{\Gamma[\theta_1,\theta_2]} dz\; z^n = \left\{\begin{array}{ll}i(\theta_2 - \theta_1), & \mathrm{if}\;n = -1 \\ \displaystyle R^{n+1}\frac{e^{i(n+1)\theta_2} - e^{i(n+1)\theta_1}}{n+1},&\mathrm{if}\;n\ne -1.\end{array}\right. \label{arcresult}\] El caso donde\(\theta_2 = \theta_1 + 2\pi\) es de particular interés. Aquí,\(\Gamma\) forma un bucle completo, y el resultado simplifica a\[\oint_{\Gamma} dz\; z^n = \left\{\begin{array}{ll}2\pi i, & \mathrm{if}\;n = -1 \\ \displaystyle 0,&\mathrm{if}\;n\ne -1,\end{array}\right. \label{simpleloop}\] lo que es independiente de, así\(R\) como la elección de\(\theta_1\) y\(\theta_2\). (Aquí, el símbolo de integración especial\(\oint\) se utiliza para indicar que la integral de contorno se toma sobre un bucle). Eq. \(\eqref{simpleloop}\)es un resultado muy importante que vamos a hacer amplio uso de más adelante.

Por cierto, ¿y si no\(n\) es un entero? En ese caso, el integrando\(z^n\) es una operación multivalorada (ver Capítulo 8), mientras que la definición de una integral de contorno asume que el integrando es una función bien definida. Para sortear este problema, podemos especificar un corte de rama y realizar el contorno integral con cualquiera de las ramas de\(z^n\) (esto está bien ya que las ramas son funciones bien definidas). Siempre y cuando el corte de rama evite cruzarse con el contorno\(\Gamma\), el resultado\(\eqref{arcresult}\) sigue siendo válido. Sin embargo,\(\Gamma\) no se puede tomar adecuadamente a lo largo de un bucle completo, ya que eso implicaría cruzar el corte de rama.