9.2: Teorema Integral de Cauchy

Una integral de bucle es una integral de contorno tomada sobre un bucle en el plano complejo; es decir, con el mismo punto inicial y final. En la Sección 9.1, encontramos el caso de una integral de bucle circular. Más generalmente, sin embargo, los contornos de bucle no son circulares sino que pueden tener otras formas.

Las integrales de bucle juegan un papel importante en el análisis complejo. Esta importancia se deriva de la siguiente propiedad, conocida como teorema integral de Cauchy:

Teorema\(\PageIndex{1}\)

Si\(f(z)\) es analítico en todas partes dentro de un bucle\(\Gamma\), entonces\(\displaystyle\oint_\Gamma dz\; f(z) = 0.\)

Prueba del teorema integral de Cauchy

El teorema integral de Cauchy se puede derivar del teorema de Stokes, que establece que para cualquier campo vectorial diferenciable\(\vec{A}(x,y,z)\) definido dentro de un espacio tridimensional, su línea integral alrededor de un bucle\(\Gamma\) es igual al flujo de su rizo a través de cualquier superficie encerrada por el bucle. Matemáticamente, esto se establece como\[\oint_\Gamma \vec{d\ell} \cdot \vec{A} = \int_{S(\Gamma)} d^2r \; \hat{n} \cdot \left(\nabla \times \vec{A}\right),\] donde\(S(\Gamma)\) denota una superficie bidimensional encerrada por el bucle\(\Gamma\), y\(\hat{n}\) denota un vector normal que sobresalga de la superficie en cada punto de integración.

Solo necesitamos la versión 2D del teorema de Stokes, en la que tanto el bucle\(\Gamma\) como la superficie encerrada\(S(\Gamma)\) están restringidos al\(x\mathrm{-}y\) plano, y de\(\vec{A}(x,y)\) igual manera no tiene\(z\) componente. Entonces el teorema de Stokes simplifica a\[\oint_\Gamma \vec{d\ell} \cdot \vec{A} = \int\!\!\!\int_{S(\Gamma)}\! dx \,dy \; \left(\frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y}\right).\]

Ahora considere una integral de bucle\[\oint_\Gamma dz \; f(z),\] donde\(\Gamma\) es una trayectoria de bucle y\(f(z)\) es alguna función analítica que es analítica en el dominio\(S(\Gamma)\). Descompongamos\(f\) en sus partes reales e imaginarias,\[f(x+iy) = u(x,y) + iv(x,y).\] La analíticidad de\(f\) implica que las funciones reales\(u\) y\(v\) son diferenciables y obedecen a las ecuaciones de Cauchy-Riemann. Ahora podemos manipular la integral de bucle de la siguiente manera:\[\begin{align} \oint_\Gamma dz \, f(z) &= \oint_\Gamma \left(dx + i dy\right) \; \left(u + i v\right) \\ &= \oint_\Gamma \Bigg(dx\, (u+iv) + dy\, (iu - v) \Bigg) \\ &= \oint_\Gamma \begin{bmatrix}dx\\dy\end{bmatrix} \cdot \begin{bmatrix}u + i v \\ iu - v\end{bmatrix} \\ &= \oint_\Gamma \vec{d\ell} \cdot \vec{A}.\end{align}\] La última expresión es una integral de línea que involucra el campo vectorial complejo\[\vec{A}(x,y) = \begin{bmatrix}u(x,y) + i v(x,y) \\ iu(x,y) - v(x,y)\end{bmatrix}.\] Usando el teorema de Stokes en 2D, convertimos esto en la integral\[\begin{align} \int\!\!\!\int_{S(\Gamma)} dx \,dy \; \left(\frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y}\right) &= \int\!\!\!\int_{S(\Gamma)} dx \,dy \; \left[\left(i\frac{\partial u}{\partial x} - \frac{\partial v}{\partial x}\right) - \left(\frac{\partial u}{\partial y} + i \frac{\partial v}{\partial y}\right)\right] \\ &= \int\!\!\!\int_{S(\Gamma)} dx \,dy \; \left[- \left(\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \right) + i\left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right)\right].\end{align}\] de área En la última línea, los dos términos entre paréntesis son ambos cero porque, según a las ecuaciones de Cauchy-Riemann,\[\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}\;\;\mathrm{and}\;\; \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}.\] Por lo tanto, la integral de bucle es cero. Q.E.D.

Consecuencias del teorema integral de Cauchy

Si el integrando no\(f(z)\) es analítico en algún lugar dentro del bucle, el teorema integral de Cauchy no se aplica, y la integral de bucle no necesita desvanecerse. En particular, supongamos que\(f(z)\) desaparece en uno o más puntos discretos dentro del bucle,\(\{z_1, z_2, \dots\}\). Entonces podemos mostrar que\[\oint_\Gamma dz\; f(z) \,=\, \sum_{n} \oint_{z_n} dz\; f(z),\] donde\(\oint_{z_n}\) denota una integral sobre un bucle de radio infinitesimal alrededor del\(n\) -ésimo punto de no analitticidad, en la misma dirección (es decir, en sentido horario o antihorario) que\(\Gamma\).

La prueba de este resultado se basa en la siguiente figura. El lazo rojo,\(\Gamma\), es el contorno sobre el que queremos integrar. El integrando es analítico en todo el área cerrada excepto en varios puntos discretos, digamos\(\{z_1, z_2, z_3\}\).

Figura\(\PageIndex{1}\)

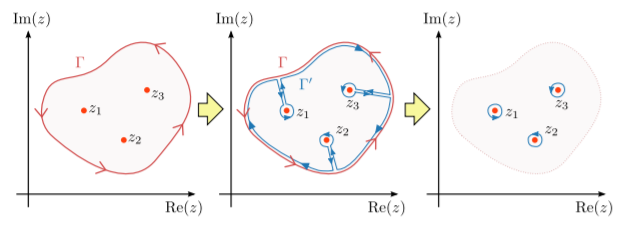
Definamos un nuevo contorno de bucle,\(\Gamma'\), mostrado por el bucle azul. Sigue la misma curva que\(\Gamma\) pero con las siguientes diferencias: (i) circunda en dirección opuesta a\(\Gamma\), (ii) contiene zarcillos que se extienden desde la curva externa a cada punto de no analitticidad, y (iii) cada zarcillo está unido a un bucle infinitesimal que rodea un punto de no analitticidad.

El bucle no\(\Gamma'\) encierra puntos de no analitticidad, por lo que el teorema integral de Cauchy dice que la integral sobre él es cero. Pero el contorno integral sobre\(\Gamma'\) puede dividirse en tres piezas: (i) la parte que sigue\(\Gamma\) pero en dirección opuesta, (ii) los zarcillos, y (iii) los bucles interiores infinitesimales:\[\begin{align} \oint_{\Gamma'}& dz\; f(z) \;\;= \;\; 0 \quad (\mathrm{by}\;\mathrm{Cauchy's}\;\mathrm{Integral}\;\mathrm{Theorem}) \\ &= \int_{\mathrm{big}\,\mathrm{loop}} dz\; f(z) + \int_{\mathrm{tendrils}} dz\; f(z) +\; \;\sum_{\mathrm{small~loop}~n}\;\; \oint_{z_n} dz\; f(z)\end{align}\] El primer término es igual al negativo de\(\oint_\Gamma dz \, f(z)\), ya que sigue un contorno que es igual a\(\Gamma\) excepción de ir por el otro lado. El segundo término es cero, porque cada zarcillo consta de dos contornos tomados en direcciones opuestas, los cuales cancelan. Por lo tanto, la ecuación anterior se reduce a\[\oint_\Gamma dz\; f(z) \,=\, \sum_n \oint_{z_n} dz\; f(z).\] La integral de contorno de bucle sobre\(\Gamma\) es igual a la suma de integrales de contorno de bucle infinitesimal que rodean cada punto de no analitticidad. Notablemente, cada uno de los bucles infinitesimales da vueltas en la misma dirección que\(\Gamma\) (por ejemplo, en sentido antihorario en la figura anterior).

Otra forma de pensar sobre esto es que el teorema integral de Cauchy dice que las regiones de analíticidad no cuentan para el valor de una integral de bucle. De ahí que podamos contraer un bucle a través de cualquier dominio en el que\(f(z)\) sea analítico, hasta que el contorno se vuelva lo más pequeño posible. Esta contracción reemplaza\(\Gamma\) con un conjunto discreto de bucles infinitesimales que encierran los puntos de no analticidad.