11.1: El oscilador armónico impulsado

Como introducción a la técnica de función de Green, estudiaremos el oscilador armónico impulsado, que es un oscilador armónico amortiguado sometido a una fuerza impulsora arbitraria. La ecuación de movimiento es\[\left[\frac{d^2}{dt^2} + 2 \gamma \frac{d}{dt} + \omega_0^2\right] x(t) = \frac{f(t)}{m}.\] Aquí,\(m\) es la masa de la partícula,\(\gamma\) es el coeficiente de amortiguación, y\(\omega_0\) es la frecuencia natural del oscilador. El lado izquierdo de la ecuación es el mismo que en la ecuación del oscilador armónico amortiguado (ver Capítulo 5). En el lado derecho, introducimos una fuerza impulsora dependiente del tiempo\(f(t)\), que actúa junto con las fuerzas preexistentes de resorte y amortiguación. Ante un arbitrariamente complicado\(f(t)\), nuestro objetivo es determinar\(x(t)\).

La función de Green para el oscilador armónico impulsado

Antes de resolver el problema del oscilador armónico impulsado para una fuerza impulsora general\(f(t)\), consideremos primero la siguiente ecuación:\[\left[\frac{\partial^2}{\partial t^2} + 2 \gamma \frac{\partial}{\partial t} + \omega_0^2\right] G(t, t') = \delta(t-t'). \label{greenfuneq}\] La función\(G(t,t')\), que depende de las dos variables\(t\) y\(t'\), se llama La función de Green. Tenga en cuenta que el operador diferencial en el lado izquierdo involucra solo derivados en\(t\).

La función de Green describe el movimiento de un oscilador armónico amortiguado sometido a una fuerza motriz particular que es una función delta, describiendo un pulso infinitesimalmente agudo centrado en\(t = t'\):\[\frac{f(t)}{m} = \delta(t-t').\] Aquí está lo bueno de\(G(t,t')\): una vez que lo conocemos, podemos encontrar un solución específica a la ecuación del oscilador armónico impulsado para cualquier\(f(t)\). La solución tiene la forma\[x(t) = \int^\infty_{-\infty} dt' \; G(t,t') \; \frac{f(t')}{m}.\] Para demostrar que esto es efectivamente una solución, enchufarlo a la ecuación de movimiento:\[\begin{align} \left[\frac{d^2}{dt^2} + 2 \gamma \frac{d}{dt} + \omega_0^2\right]\, x(t) &= \int^\infty_{-\infty} dt' \; \left[\frac{\partial^2}{\partial t^2} + 2 \gamma \frac{\partial}{\partial t} + \omega_0^2\right] G(t,t') \frac{f(t')}{m} \\ &= \int^\infty_{-\infty} dt' \; \delta(t-t')\, \frac{f(t')}{m} \\ &= \frac{f(t)}{m}.\end{align}\] Tenga en cuenta que podemos mover el operador diferencial dentro de la integral porque\(t\) y\(t'\) son variables independientes.

El concepto de función de Green se basa en el principio de superposición. El movimiento del oscilador es inducido por la fuerza impulsora, pero el valor de\(x(t)\) en el tiempo\(t\) no depende solo del valor instantáneo de\(f(t)\) en el tiempo\(t\); en cambio, depende de los valores de\(f(t')\) sobre todo tiempos pasados\(t' < t\). Así podemos descomponernos\(f\) en una superposición de pulsos descritos por funciones delta en diferentes momentos. Entonces\(x(t)\) es una superposición de las oscilaciones producidas por los pulsos individuales.

Encontrar la función del verde

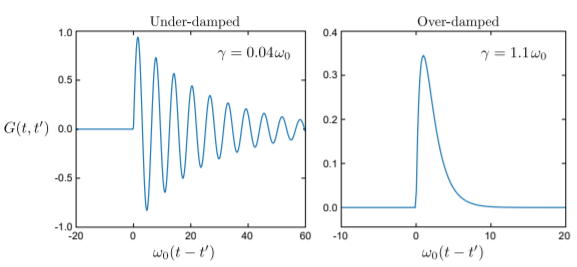
Para encontrar la función de Green, podemos usar la transformada de Fourier. Supongamos que la transformada de Fourier de\(G(t,t')\) con respecto a\(t\) es convergente, y que el oscilador no está amortiguado críticamente (es decir\(\omega_0 \ne \gamma\); ver Sección 5.3). La transformación de Fourier de la función de Green (también llamada función de Green en el dominio de frecuencia) es\[G(\omega, t') = \int_{-\infty}^\infty dt \; e^{i\omega t}\, G(t,t').\] Aquí, hemos utilizado la convención de signos para las transformaciones de Fourier en el dominio del tiempo (ver Sección 10.3). Aplicando la transformada de Fourier a ambos lados de la ecuación de función de Green, y haciendo uso de cómo se comportan las derivadas bajo la transformación de Fourier (ver Sección 10.4), da\[\left[- \omega^2 - 2i \gamma\omega + \omega_0^2\right] G(\omega,t') = \int_{-\infty}^\infty dt \; e^{i\omega t}\, \delta(t-t') = e^{i\omega t'}. \label{green-omega}\] La ecuación diferencial para se\(G(t,t')\) ha convertido así en una ecuación algebraica para \(G(\omega,t')\), cuya solución es\[G(\omega, t') = - \frac{e^{i\omega t'}}{\omega^2 + 2i\gamma\omega - \omega_0^2}.\] Finalmente, recuperamos la solución de dominio de tiempo mediante el uso de la transformada inversa de Fourier:\[\begin{align} G(t,t') &= \int_{-\infty}^\infty \frac{d\omega}{2\pi} \, e^{-i\omega t} G(\omega, t') \\ &= - \int_{-\infty}^\infty \frac{d\omega}{2\pi} \, \frac{e^{-i\omega (t-t')}}{\omega^2 + 2i\gamma\omega - \omega_0^2}.\end{align}\] El denominador de la integral es una expresión cuadrática, por lo que esta puede reescribirse como:\[G(t,t') = - \int_{-\infty}^\infty \frac{d\omega}{2\pi} \, \frac{e^{-i\omega (t-t')}}{(\omega - \omega_+)(\omega - \omega_-)} \quad\mathrm{where}\;\; \omega_{\pm} = -i\gamma \pm \sqrt{\omega_0^2-\gamma^2}.\] Esto puede ser evaluado por integración de contorno. El integrando tiene dos polos, que son precisamente las frecuencias complejas del oscilador armónico amortiguado; ambos se encuentran en el plano complejo negativo. Porque\(t < t'\), el lema de Jordan requiere que cerremos el contorno en el medio plano superior, encerrando ninguno de los polos, por lo que la integral es cero. Para\(t > t'\), debemos cerrar el contorno en el medio plano inferior, encerrando ambos polos, por lo que el resultado es\[\begin{align} G(t,t') &= i \Theta(t-t') \, \left[ \frac{e^{-i\omega_+ (t-t')}}{\omega_+ - \omega_- } + \frac{e^{-i\omega_- (t-t')}}{\omega_- - \omega_+}\right] \\ &= \Theta(t-t') \;e^{-\gamma(t-t')} \; \times \left\{\begin{array}{ll} \frac{1}{\sqrt{\omega_0^2-\gamma^2}}\, \sin\left[\sqrt{\omega_0^2-\gamma^2} (t-t')\right], & \gamma < \omega_0, \\ \frac{1}{\sqrt{\gamma^2-\omega_0^2}}\, \sinh\left[\sqrt{\gamma^2-\omega_0^2} (t-t')\right], & \gamma > \omega_0. \end{array}\right. \label{greensol}\end{align}\] Aquí,\(\Theta(t-t')\) se refiere a la función de paso\[\Theta(\tau) = \left\{\begin{array}{ll} 1, &\;\;\;\textrm{for} \; \tau \ge 0\\ 0,&\;\;\; \textrm{otherwise.}\end{array}\right.\] El resultado se traza en la figura de abajo para dos opciones diferentes de\(\gamma\) y \(\omega_0\). La solución para el caso críticamente amortiguado,\(\gamma = \omega_0\), se deja como un ejercicio.

Figura\(\PageIndex{1}\)

Características de la función de Green

Como se señaló anteriormente, la función de Green en el dominio del tiempo tiene un significado físico: representa el movimiento del oscilador en respuesta a un pulso de fuerza,\(f(t) = m\, \delta(t-t')\). Examinemos con mayor detalle el resultado obtenido en el apartado anterior, para ver si coincide con nuestra intuición física.

Lo primero que hay que notar es que la función del Verde depende de\(t\) y\(t'\) sólo en la combinación\(t-t'\). Esto tiene sentido: la respuesta del oscilador al pulso de fuerza solo debe depender del tiempo transcurrido desde el pulso. Podemos aprovechar esta propiedad redefiniendo la función de Green en el dominio de frecuencia como la\[G(\omega) = \int_{-\infty}^\infty dt \; e^{i\omega (t-t')}\, G(t-t'),\] que luego obedece\[\left[- \omega^2 - 2i \gamma\omega + \omega_0^2\right] G(\omega) = 1.\] Esto es más agradable para trabajar que la Eq. \(\eqref{green-omega}\)ya que no hay ninguna\(t'\) variable extraña presente.

A continuación, observe cómo se comporta la función del Green justo antes y después del pulso. Su valor es cero para todos\(t - t' < 0\) (es decir, antes del pulso). Esta característica se discutirá con mayor detalle en la siguiente sección. Además, no hay discontinuidad en\(x(t)\) at\(t - t' = 0\); el pulso de fuerza no hace que el oscilador se “teletransporte” instantáneamente a una posición diferente. En cambio, produce una discontinuidad en la velocidad del oscilador.

Podemos calcular la discontinuidad de la velocidad integrando la ecuación de la función de Green en un intervalo infinitesimal de tiempo que rodea\(t'\):\[\begin{align} \lim_{\epsilon \rightarrow 0} \int_{t'-\epsilon}^{t'+\epsilon} dt \left[\frac{\partial^2}{\partial t^2} + 2\gamma\frac{\partial}{\partial t} + \omega_0^2\right] G(t,t') &= \lim_{\epsilon \rightarrow 0} \int_{t'-\epsilon}^{t'+\epsilon} dt \; \delta(t-t') \\ = \lim_{\epsilon \rightarrow 0} \left\{ \left.\frac{\partial G(t,t')}{\partial t}\right|_{t = t' +\epsilon} - \left.\frac{\partial G(t,t')}{\partial t}\right|_{t = t' - \epsilon}\right\} &= 1.\end{align}\] En la última línea, la expresión en el lado izquierdo representa la diferencia entre las velocidades justo después y antes del pulso. Evidentemente, el pulso imparte una unidad de velocidad a\(t=t'\). Al observar las soluciones obtenidas en la Sección 11.1, podemos verificarlas\(\partial G/\partial t = 0\) justo antes del pulso, y\(\partial G/\partial t = 1\) justo después de él.

Para\(t - t' > 0\), la fuerza aplicada vuelve a cero, y el sistema se comporta como el oscilador armónico no accionado. Si el oscilador está subamortiguado (\(\gamma < \omega_0\)), sufre una oscilación en descomposición alrededor del origen. Si el oscilador está sobreamortiguado (\(\gamma > \omega_0\)), avanza una distancia, luego se asienta exponencialmente de regreso al origen.

Causalidad

Hemos visto que la moción\(x(t)\) debe depender de la fuerza impulsora\(f(t')\) en todos los tiempos pasados\(t' < t\), pero no debe depender de la fuerza en tiempos futuros. Por la relación\[x(t) = \int_{-\infty}^\infty dt'\; G(t,t')\, \frac{f(t')}{m},\] esto significa que la función del Verde debe satisfacer\[G(t,t') = 0 \;\; \mathrm{for}\;\; t -t' < 0.\] Esta condición es referida como causalidad, porque equivale a decir que la causa debe preceder al efecto. La función de un Green con esta característica se llama función causal de Green.

Para el oscilador armónico impulsado, la función de Green en el dominio del tiempo satisface una ecuación diferencial de segundo orden, por lo que su solución general debe contener dos parámetros libres. La solución específica que derivamos anteriormente, la Ec. \(\eqref{greensol}\), resulta ser la única solución causal. Hay un par de maneras de ver por qué.

La primera forma es observar que para\(t > t'\), la función de Green satisface la ecuación diferencial para el oscilador armónico no impulsado. Pero con base en la discusión en la Sección 11.1, la función causal del Verde necesita obedecer dos condiciones en\(t = t' + 0^+\): (i)\(G = 0\), y (ii)\(\partial G / \partial t = 1\). Estas actúan como dos condiciones límite para la ecuación del oscilador armónico no impulsado, dando lugar a la solución específica que encontramos.

La otra forma de ver que la función causal de Green es única es imaginar agregar a nuestra solución específica cualquier solución\(x_1(t)\) para el oscilador armónico no impulsado. Se verifica fácilmente que el resultante\(G(t,t')\) es también una solución a la Ec. \(\eqref{greenfuneq}\). Dado que la solución general para\(x_1(t)\) contiene dos parámetros libres, hemos encontrado así la solución general para\(G(t,t')\). Pero las soluciones para\(x_1(t)\) son todas infinitas en el\(t \rightarrow -\infty\) límite, a excepción de la solución trivial\(x_1(t) = 0\). Esa elección corresponde a la función causal del Green\(\eqref{greensol}\).