24.2: Reflexión, Refracción y Dispersión

objetivos de aprendizaje

• Formular la relación entre el ángulo de reflexión y el ángulo de incidencia

Cada vez que te miras a un espejo o entrecerras los ojos ante la luz del sol que resplandezca en un lago, estás viendo un reflejo. Cuando miras el texto de un libro, en realidad estás viendo la luz que se refleja en él. Los telescopios grandes utilizan reflejos para formar imágenes de estrellas y otros objetos astronómicos. De hecho, la única manera de ver un objeto que no emite luz por sí mismo es si ese objeto refleja la luz.

La ley de la reflexión se ilustra en, que también muestra cómo se miden los ángulos con relación a la perpendicular a la superficie en el punto donde incide el rayo de luz. La ley de la reflexión es muy simple: El ángulo de reflexión es igual al ángulo de incidencia. Cuando vemos nuestro reflejo en un espejo, parece que nuestra imagen está en realidad detrás del espejo —vemos la luz proveniente de una dirección determinada por la ley de la reflexión. Los ángulos son tales que nuestra imagen aparece exactamente a la misma distancia detrás del espejo mientras nos mantenemos alejados del espejo.

Reflejo del espejo: Una imagen en un espejo aparece como si estuviera detrás del espejo. Los dos rayos mostrados son aquellos que golpean el espejo apenas en los ángulos correctos para ser reflejados en los ojos del espectador. La imagen parece provenir de la dirección de la que provienen los rayos cuando entran en los ojos del espectador.

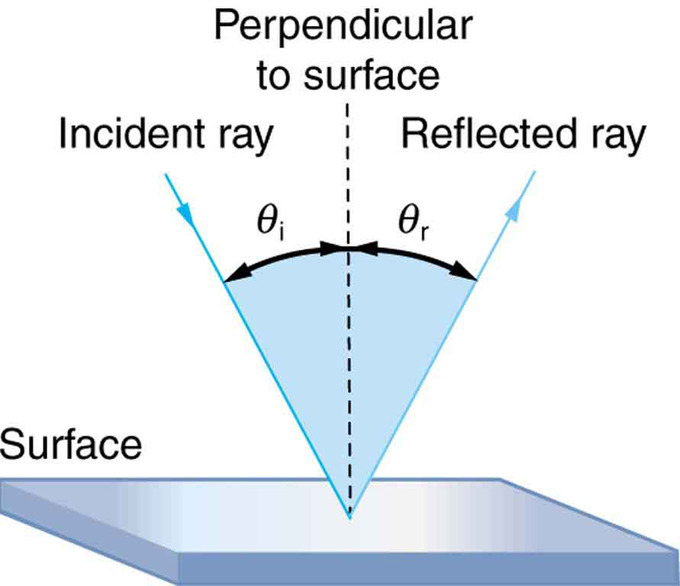
Ley de Reflexión: La ley de reflexión establece que el ángulo de reflexión es igual al ángulo de incidencia: θr = θi. Los ángulos se miden en relación con la perpendicular a la superficie en el punto donde el rayo golpea la superficie.

Esperamos ver reflejos en una superficie lisa. Sin embargo, la luz golpea diferentes partes de una superficie rugosa en diferentes ángulos, y se refleja en muchas direcciones diferentes (“difusa”). La luz difusa es lo que nos permite ver una hoja de papel desde cualquier ángulo. Muchos objetos, como personas, ropa, hojas y paredes, tienen superficies rugosas y se pueden ver desde todos los lados. Un espejo, por otro lado, tiene una superficie lisa (en comparación con la longitud de onda de la luz) y refleja la luz en ángulos específicos. Cuando la luna se refleja en la superficie de un lago, se produce una combinación de estos efectos.

Reflexión: Un breve panorama de la reflexión y la ley de la reflexión.

La ley de la refracción: la ley de Snell y el índice de refracción

La cantidad que un rayo de luz cambia de dirección depende tanto del ángulo incidente como de la cantidad que cambia la velocidad.

objetivos de aprendizaje

• Formular la relación entre el índice de refracción y la velocidad de la luz

Es fácil notar algunas cosas extrañas al mirar dentro de una pecera. Por ejemplo, es posible que veas que el mismo pez parece estar en dos lugares diferentes. Esto se debe a que la luz que viene de los peces hacia nosotros cambia de dirección cuando sale del tanque, y en este caso, puede recorrer dos caminos diferentes para llegar a nuestros ojos. El cambio de dirección de un rayo de luz (vagamente llamado flexión) cuando pasa por variaciones en la materia se llama refracción. La refracción es responsable de una tremenda gama de fenómenos ópticos, desde la acción de lentes hasta la transmisión de voz a través de fibras ópticas.

Ley de Refracción: Mirando la pecera como se muestra, podemos ver el mismo pez en dos ubicaciones diferentes, porque la luz cambia de dirección cuando pasa de agua a aire. En este caso, la luz puede llegar al observador por dos caminos diferentes, y así el pez parece estar en dos lugares diferentes. Esta flexión de la luz se llama refracción y es responsable de muchos fenómenos ópticos.

Refracción: El cambio de dirección de un rayo de luz (vagamente llamado flexión) cuando pasa por variaciones en la materia se llama refracción.

Velocidad de la luz

La velocidad de la luz c no sólo afecta a la refracción, es uno de los conceptos centrales de la teoría de la relatividad de Einstein. La velocidad de la luz varía de manera precisa con el material que atraviesa. Hace conexiones entre el espacio y el tiempo y altera nuestras expectativas de que todos los observadores midan el mismo tiempo para un mismo evento, por ejemplo. La velocidad de la luz es tan importante que su valor en un vacío es una de las constantes más fundamentales en la naturaleza además de ser una de las cuatro unidades SI fundamentales.

¿Por qué la luz cambia de dirección al pasar de un material (medio) a otro? Es porque la luz cambia de velocidad al pasar de un material a otro.

Ley de Refracción

Un rayo de luz cambia de dirección cuando pasa de un medio a otro. Como antes, los ángulos se miden con relación a una perpendicular a la superficie en el punto donde el rayo de luz la cruza. El cambio de dirección del rayo de luz depende de cómo cambie la velocidad de la luz. El cambio en la velocidad de la luz está relacionado con los índices de refracción de los medios involucrados. En los medios que tienen un mayor índice de refracción la velocidad de la luz es menor. Imagina mover tu mano por el aire y luego moverla a través de un cuerpo de agua. Es más difícil mover tu mano por el agua, y así tu mano se ralentiza si estás aplicando la misma cantidad de fuerza. De igual manera, la luz viaja más despacio cuando se mueve a través de medios que tienen mayores índices de refracción.

La cantidad que un rayo de luz cambia de dirección depende tanto del ángulo incidente como de la cantidad que cambia la velocidad. Para un rayo en un ángulo incidente dado, un gran cambio en la velocidad provoca un gran cambio de dirección y, por lo tanto, un gran cambio en el ángulo. La relación matemática exacta es la ley de la refracción, o “Ley de Snell”, que se afirma en forma de ecuación como:

\[\mathrm{n_1 \sin \theta _1 = n_2 \sin \theta _2}\]

Aquí n ₁ y n ₂ son los índices de refracción para el medio 1 y 2, y θ ₁ y θ ₂ son los ángulos entre los rayos y la perpendicular en medio 1 y 2. El rayo entrante se llama el rayo incidente y el rayo saliente el rayo refractado, y los ángulos asociados el ángulo incidente y el ángulo refractado. La ley de la refracción también se llama ley de Snell en función del matemático holandés Willebrord Snell, quien la descubrió en 1621. Los experimentos de Snell mostraron que se obedecía la ley de refracción y que se podía asignar un índice característico de refracción n a un medio dado.

Entendiendo la Ley de Snell con el Índice de Refracción: Este video introduce la refracción con la Ley de Snell y el índice de refracción.El segundo video discute en detalle la reflexión interna total (TIR). http://www.youtube.com/watch?v=fvrvqm3Erzk

Reflejo Interno Total y Fibra Óptica

La reflexión interna total ocurre cuando una onda que se propaga golpea un límite medio en un ángulo mayor que un ángulo crítico particular.

objetivos de aprendizaje

• Formular las condiciones requeridas para la reflexión interna total

La reflexión interna total es un fenómeno que ocurre cuando una onda propagadora golpea un límite medio en un ángulo mayor que un ángulo crítico particular con respecto a la normal a la superficie. Si el índice de refracción es menor en el otro lado del límite y el ángulo incidente es mayor que el ángulo crítico, la onda no puede atravesar y se refleja por completo. El ángulo crítico es el ángulo de incidencia por encima del cual se produce la reflectancia interna total.

¿Qué es la Reflexión Interna Total? : Describe el concepto de reflexión interna total, deriva la ecuación para el ángulo crítico y muestra un ejemplo.

Ángulo crítico

El ángulo crítico es el ángulo de incidencia por encima del cual se produce la reflexión interna total. El ángulo de incidencia se mide con respecto a la normal en el límite de refracción (ver diagrama que ilustra la ley de Snell). Considera un rayo de luz que pasa del vidrio al aire. La luz que emana de la interfaz se dobla hacia el vidrio. Cuando el ángulo incidente se incrementa suficientemente, el ángulo transmitido (en el aire) alcanza los 90 grados. Es en este punto no se transmite luz al aire. El ángulo crítico θcθc viene dado por la ley de Snell, n1sinθ1=n2sinθ2n1sinθ1=n2sinθ2. Aquí, _n1 y n ₂ son índices de refracción de los medios, y θ1θ1 y θ2θ2 son ángulos de incidencia y refracción, respectivamente. Para encontrar el ángulo crítico, encontramos el valor para θ1θ1 cuando θ2θ2= 90° y así sinθ2=1sinθ2=1. El valor resultante de θ1θ1 es igual al ángulo crítico θc=θ1=arcsin (n2n1) θc=θ1=arcsin (n2n1). Por lo que el ángulo crítico sólo se define cuando n ₂ /n ₁ es menor que 1.

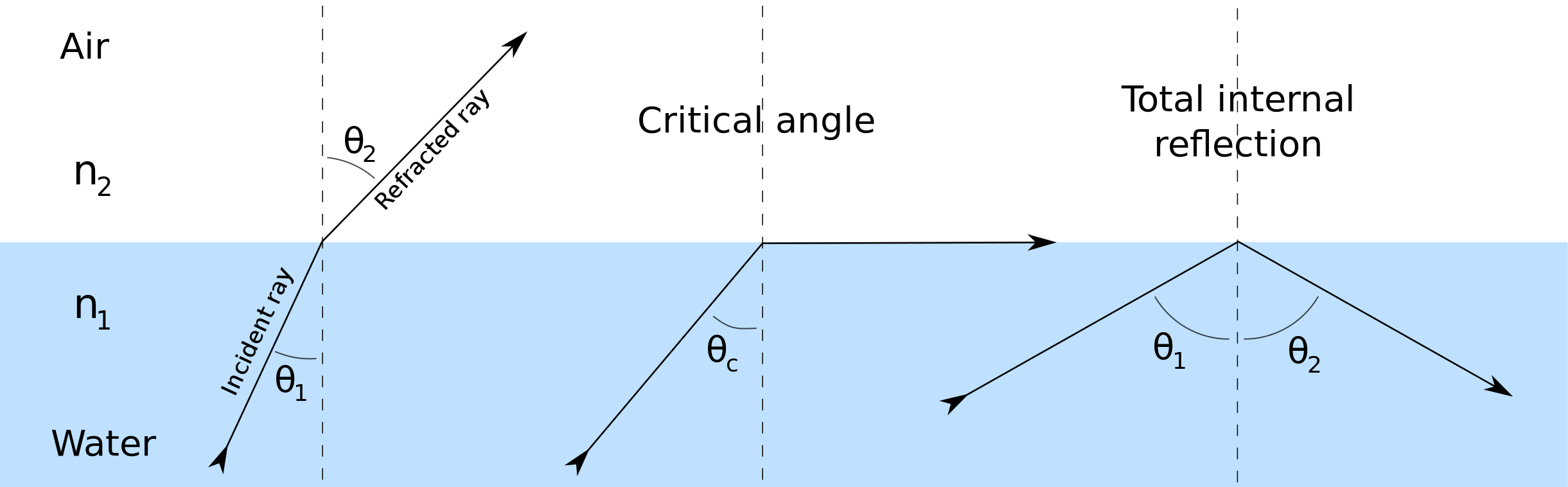
Fig 1: Refracción de la luz en la interfaz entre dos medios, incluyendo la reflexión interna total.

Fibra Óptica

La reflexión interna total es una herramienta poderosa ya que puede ser utilizada para confinar la luz. Una de las aplicaciones más comunes de la reflexión interna total es en la fibra óptica. Una fibra óptica es una fibra delgada y transparente, generalmente hecha de vidrio o plástico, para transmitir luz. La construcción de una sola fibra óptica se muestra en.

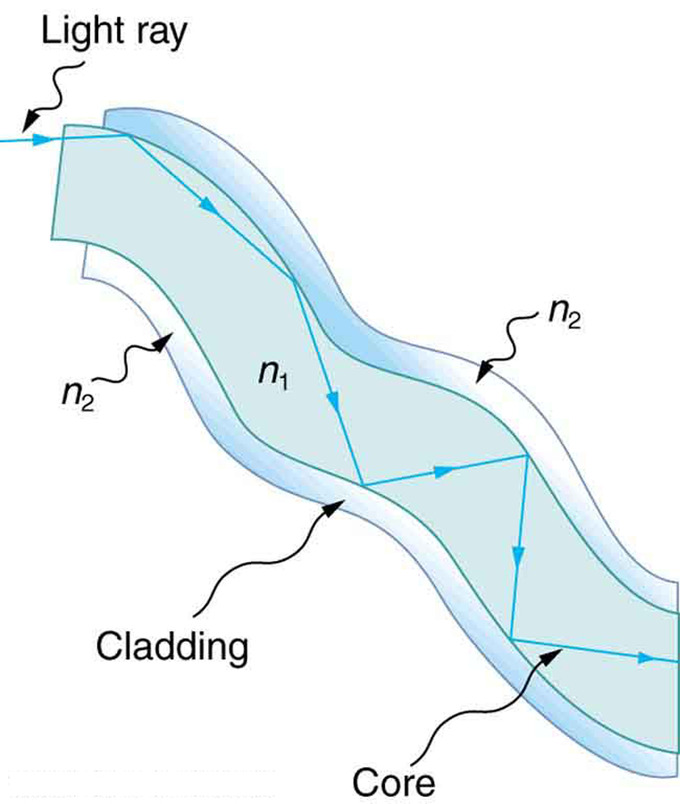
Fig 2: Las fibras en haces están revestidas por un material que tiene un índice de refracción menor que el núcleo para asegurar una reflexión interna total, incluso cuando las fibras están en contacto entre sí. Esto muestra una sola fibra con su revestimiento.

La estructura funcional básica de una fibra óptica consiste en un revestimiento protector exterior y un núcleo interno a través del cual viajan los pulsos de luz. El diámetro total de la fibra es de aproximadamente 125 μm y el del núcleo es de aproximadamente 50 μm. La diferencia en el índice de refracción del revestimiento y el núcleo permite una reflexión interna total de la misma manera que ocurre en una superficie aire-agua que se muestra en. Si la luz incide en el extremo de un cable con un ángulo de incidencia mayor que el ángulo crítico, entonces la luz permanecerá atrapada dentro del hilo de vidrio. De esta manera, la luz viaja muy rápidamente por la longitud del cable en una distancia muy larga (decenas de kilómetros). Las fibras ópticas se utilizan comúnmente en las telecomunicaciones, ya que la información puede transportarse a largas distancias, con una pérdida mínima de datos. Otro uso común se puede encontrar en medicina en endoscopios. El campo de la ciencia aplicada y la ingeniería que se ocupa del diseño y aplicación de fibras ópticas se denominan fibra óptica.

Polarización Total

El ángulo de Brewster es un ángulo de incidencia en el que la luz con una polarización particular se transmite perfectamente a través de una superficie.

objetivos de aprendizaje

• Calcular el ángulo de Brewster a partir de los índices de refracción y discutir su mecanismo físico

El ángulo de Brewster (también conocido como ángulo de polarización) es un ángulo de incidencia en el que la luz con una polarización particular se transmite perfectamente a través de una superficie dieléctrica transparente, sin reflexión. Cuando la luz no polarizada incide en este ángulo, la luz que se refleja desde la superficie es, por lo tanto, perfectamente polarizada. Este ángulo especial de incidencia lleva el nombre del físico escocés Sir David Brewster (1781—1868).

El mecanismo físico para esto se puede entender cualitativamente a partir de la manera en que los dipolos eléctricos en los medios responden a la luz polarizada p (cuyo campo eléctrico está polarizado en el mismo plano que el rayo incidente y la superficie normal). Uno puede imaginar que la luz incidente en la superficie es absorbida, y luego re-radiada por dipolos eléctricos oscilantes en la interfaz entre los dos medios. La luz refractada se emite perpendicular a la dirección del momento dipolar; no se puede irradiar energía en la dirección del momento dipolar. Así, si el ángulo de reflexión θ ₁ (ángulo de reflexión) es igual a la alineación de los dipolos (90 — θ ₂), donde θ ₂ es ángulo de refracción, no se refleja luz.

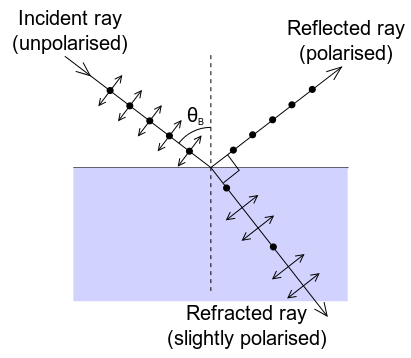
Fig. 1: Una ilustración de la polarización de la luz que incide en una interfaz en el ángulo de Brewster.

Esta condición geométrica se puede expresar como\(\theta _ { 1 } + \theta _ { 2 } = 90 ^ { \circ }\), donde θ ₁ es el ángulo de incidencia y θ ₂ es el ángulo de refracción. Usando la ley de Snell (n ₁ sinθ1 = n ₂ sinθ ₂), se puede calcular el ángulo de incidencia θ ₁ = _B en el que no se refleja luz:\(\mathrm { n } _ { 1 } \sin \left( \theta _ { \mathrm { B } } \right) = \mathrm { n } _ { 2 } \sin \left( 90 ^ { \circ } - \theta _ { \mathrm { B } } \right)\) Resolviendo para θ _B da\(\theta _ { \mathrm { B } } = \arctan \left( \frac { \mathrm { n } _ { 2 } } { \mathrm { n } _ { 1 } } \right)\).

Cuando la luz golpea una superficie en un ángulo Brewster, el haz reflejado se polariza linealmente. Muestra un ejemplo, donde el haz reflejado estaba casi perfectamente polarizado y por lo tanto, bloqueado por un polarizador en la imagen derecha. Las gafas de sol polarizadas utilizan el mismo principio para reducir el deslumbramiento del sol reflejándose en superficies horizontales como el agua o la carretera.

Fig 2: Fotografía tomada de una ventana con un filtro polarizador de cámara girado a dos ángulos diferentes. En la imagen de la izquierda, el polarizador se alinea con el ángulo de polarización de la reflexión de la ventana. En la imagen de la derecha, el polarizador se ha girado 90° eliminando la luz solar reflejada fuertemente polarizada.

Experiencia de polarización: Un filtro polarizador permite que pase la luz de un plano particular de polarización, pero dispersa el resto de la luz. Cuando se cruzan dos filtros polarizantes, casi no pasa luz. Algunos materiales tienen moléculas que giran el plano de polarización de la luz. Cuando uno de estos materiales se coloca entre filtros polarizadores cruzados, se permite que pase más luz.

Dispersión: Arcoíris y Prisims

La dispersión se define como la difusión de la luz blanca en su espectro completo de longitudes de onda.

objetivos de aprendizaje

• Describir la producción de arcoíris mediante una combinación de procesos de refracción y reflexión

Vemos alrededor de seis colores en un arco iris: rojo, naranja, amarillo, verde, azul y violeta; a veces el índigo también aparece en la lista. Estos colores están asociados con diferentes longitudes de onda de luz. La luz blanca, en particular, es una mezcla bastante uniforme de todas las longitudes de onda visibles. La luz solar, considerada blanca, en realidad parece ser un poco amarilla debido a su mezcla de longitudes de onda, pero sí contiene todas las longitudes de onda visibles. La secuencia de colores en arcoíris es la misma secuencia que los colores trazados versus longitud de onda. Lo que esto implica es que la luz blanca se extiende según la longitud de onda en un arco iris. La dispersión se define como la difusión de la luz blanca en su espectro completo de longitudes de onda. Más técnicamente, la dispersión ocurre siempre que hay un proceso que cambia la dirección de la luz de una manera que depende de la longitud de onda. La dispersión, como fenómeno general, puede ocurrir para cualquier tipo de onda y siempre implica procesos dependientes de la longitud de onda.

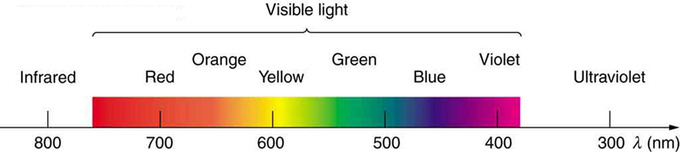
Colores de un arco iris: A pesar de que los arcoíris están asociados con siete colores, el arco iris es una distribución continua de colores según las longitudes de onda.

La refracción es responsable de la dispersión en los arcoíris y muchas otras situaciones. El ángulo de refracción depende del índice de refracción, como vimos en la Ley de Refracción. Sabemos que el índice de refracción n depende del medio. Pero para un medio dado, n también depende de la longitud de onda. Tenga en cuenta que, para un medio dado, n aumenta a medida que disminuye la longitud de onda y es mayor para la luz violeta. Así, la luz violeta se dobla más que la luz roja y la luz se dispersa en la misma secuencia de longitudes de onda.

Luz pura y dispersión de luz: (a) Una longitud de onda pura de luz cae sobre un prisma y se refracta en ambas superficies. (b) La luz blanca es dispersada por el prisma (se muestra exagerada). Dado que el índice de refracción varía con la longitud de onda, los ángulos de refracción varían con la longitud de onda. Se produce una secuencia de rojo a violeta, debido a que el índice de refracción aumenta de manera constante con la disminución de la longitud de onda.

Los arcoíris son producidos por una combinación de refracción y reflexión. Es posible que hayas notado que ves un arcoíris solo cuando apartas la mirada del sol. La luz entra en una gota de agua y se refleja desde la parte posterior de la gota. La luz se refracta tanto a medida que entra como a medida que sale de la gota. Dado que el índice de refracción del agua varía con la longitud de onda, la luz se dispersa y se observa un arco iris. (No hay dispersión causada por la reflexión en la superficie posterior, ya que la ley de la reflexión no depende de la longitud de onda) El arco iris real de colores visto por un observador depende de la miríada de rayos que se refractan y reflejan hacia los ojos del observador a partir de numerosas gotas de agua. El arco de un arco iris proviene de la necesidad de estar mirando un ángulo específico relativo a la dirección del sol.

Luz que se refleja en la gotita de agua: Parte de la luz que cae sobre esta gota de agua entra y se refleja desde la parte posterior de la gota. Esta luz se refracta y dispersa tanto a medida que entra como a medida que sale de la gota.

Puntos Clave

• La luz incide en diferentes partes de una superficie rugosa en diferentes ángulos y se refleja, o difunde, en muchas direcciones diferentes.
• Un espejo tiene una superficie lisa (en comparación con la longitud de onda de la luz) y así refleja la luz en ángulos específicos.
• Vemos la luz reflejada en un espejo proveniente de una dirección determinada por la ley de la reflexión.
• El cambio de dirección de un rayo de luz (vagamente llamado flexión) cuando pasa por variaciones en la materia se llama refracción.
• El índice de refracción es n=c/v, donde v es la velocidad de la luz en el material, c es la velocidad de la luz en vacío y n es el índice de refracción.
• La ley de Snell, la ley de la refracción, se establece en forma de ecuación como n1sinθ1=n2sinθ2n1sinθ1=n2sinθ2.
• El ángulo crítico es el ángulo de incidencia por encima del cual se produce la reflexión interna total y dado como θc=arcsin (n2n1) θc=arcsin (n2n1).
• El ángulo crítico solo se define cuando n2/n1 es menor que 1.
• Si la luz incide sobre una fibra óptica con un ángulo de incidencia mayor que el ángulo crítico, entonces la luz permanecerá atrapada dentro de la hebra de vidrio. La luz puede recorrer una distancia muy larga sin una pérdida significativa.
• Cuando la luz golpea una superficie en un ángulo de Brewster, el haz reflejado se polariza linealmente.
• El mecanismo físico para el ángulo de Brewster se puede entender cualitativamente a partir de la manera en que los dipolos eléctricos en los medios responden a la luz polarizada p.
• El ángulo de Brewsters se da como θB=ArcTan (n2n1) θB=ArcTan (n2n1).
• La dispersión ocurre siempre que hay un proceso que cambia la dirección de la luz de una manera que depende de la longitud de onda. La dispersión puede ocurrir para cualquier tipo de onda y siempre implica procesos dependientes de la longitud de onda.
• Para un medio dado, n aumenta a medida que disminuye la longitud de onda y es mayor para la luz violeta. Así, la luz violeta se dobla más que la luz roja, como puede verse con un prisma.
• En un arco iris, la luz entra en una gota de agua y se refleja desde la parte posterior de la gota. La luz se refracta tanto a medida que entra como a medida que sale de la gota.

Términos Clave

• reflexión: la propiedad de una onda propagada que es arrojada hacia atrás desde una superficie (como un espejo)
• refracción: Cambio de dirección de un rayo de luz cuando pasa por variaciones en la materia.
• índice de refracción: Para un material, la relación entre la velocidad de la luz en el vacío y la del material.
• Ley de Snell: Una fórmula utilizada para describir la relación entre los ángulos de incidencia y refracción.
• revestimiento: Una o más capas de materiales de menor índice de refracción, en contacto íntimo con un material de núcleo de mayor índice de refracción.
• dipolo: Separación de cargas positivas y negativas.
• dieléctrico: Un material eléctricamente aislante o no conductor considerado por su susceptibilidad eléctrica (es decir, su propiedad de polarización cuando se expone a un campo eléctrico externo).
• polarizador: Un filtro óptico que pasa luz de una polarización específica y bloquea ondas de otras polarizaciones.

LICENCIAS Y ATRIBUCIONES

CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

• Curación y Revisión. Proporcionado por: Boundless.com. Licencia: CC BY-SA: Atribución-CompartirIgual

CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

• Colegio OpenStax, Colegio de Física. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42456/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Proporcionado por: Luz y Materia. Ubicado en: http://lightandmatter.com/simpleo.pdf. Licencia: CC BY: Atribución
• reflexión. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/reflection. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42456/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Reflexión. Ubicado en: http://www.youtube.com/watch?v=XaJ4WYV2gyk. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42456/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42459/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//fisics/definición/refracción. Licencia: CC BY-SA: Atribución-CompartirIgual
• índice de refracción. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/index+de+refracción. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42456/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Reflexión. Ubicado en: http://www.youtube.com/watch?v=XaJ4WYV2gyk. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42456/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42459/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Entendiendo la Ley de Snell con el Índice de Refracción. Ubicado en: http://www.youtube.com/watch?v=s6IGWO3e2Wo. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Proyecto Libre de Textos de Ciencias de Preparatoria, Óptica Geométrica: Reflexión Interna Total. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m40070/latest/. Licencia: CC BY: Atribución
• Fibra óptica. Proporcionado por: Wikipedia. Ubicado en: http://en.Wikipedia.org/wiki/Fiber_optics. Licencia: CC BY-SA: Atribución-CompartirIgual
• Reflexión interna total. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Total_Internal_Reflection. Licencia: CC BY-SA: Atribución-CompartirIgual
• revestimiento. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Revestimiento. Licencia: CC BY-SA: Atribución-CompartirIgual
• Ley de Snell. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Snell's%20Law. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42456/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Reflexión. Ubicado en: http://www.youtube.com/watch?v=XaJ4WYV2gyk. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42456/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42459/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Entendiendo la Ley de Snell con el Índice de Refracción. Ubicado en: http://www.youtube.com/watch?v=s6IGWO3e2Wo. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Colegio OpenStax, Reflexión Interna Total. 29 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42462/latest/. Licencia: CC BY: Atribución
• Reflexión interna total. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Total_Internal_Reflection. Licencia: CC BY: Atribución
• ¿Qué es la Reflexión Interna Total?. Ubicado en: http://www.youtube.com/watch?v=NXGLBMTtk40. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Ángulo de Brewster. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Brewster's_Angle. Licencia: CC BY-SA: Atribución-CompartirIgual
• dipolo. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/dipole. Licencia: CC BY-SA: Atribución-CompartirIgual
• polarizador. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Polarizer. Licencia: CC BY-SA: Atribución-CompartirIgual
• dieléctrico. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/dieléctrico. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42456/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Reflexión. Ubicado en: http://www.youtube.com/watch?v=XaJ4WYV2gyk. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42456/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42459/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Entendiendo la Ley de Snell con el Índice de Refracción. Ubicado en: http://www.youtube.com/watch?v=s6IGWO3e2Wo. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Colegio OpenStax, Reflexión Interna Total. 29 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42462/latest/. Licencia: CC BY: Atribución
• Reflexión interna total. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Total_Internal_Reflection. Licencia: CC BY: Atribución
• ¿Qué es la Reflexión Interna Total?. Ubicado en: http://www.youtube.com/watch?v=NXGLBMTtk40. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Experiencia de Polarización. Ubicado en: http://www.youtube.com/watch?v=Qv7Y-Er7rgc. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Ángulo de Brewster. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Brewster's_Angle. Licencia: CC BY: Atribución
• Ángulo de Brewster. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Brewster's_Angle. Licencia: CC BY: Atribución
• OpenStax College, Dispersión: El arco iris y los prismas. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42466/latest/. Licencia: CC BY: Atribución
• Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//fisics/definición/refracción. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42456/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Reflexión. Ubicado en: http://www.youtube.com/watch?v=XaJ4WYV2gyk. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42456/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 10 de noviembre de 2012. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42459/latest/?collection=col11406/1.7. Licencia: CC BY: Atribución
• Entendiendo la Ley de Snell con el Índice de Refracción. Ubicado en: http://www.youtube.com/watch?v=s6IGWO3e2Wo. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Colegio OpenStax, Reflexión Interna Total. 29 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42462/latest/. Licencia: CC BY: Atribución
• Reflexión interna total. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Total_Internal_Reflection. Licencia: CC BY: Atribución
• ¿Qué es la Reflexión Interna Total?. Ubicado en: http://www.youtube.com/watch?v=NXGLBMTtk40. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Experiencia de Polarización. Ubicado en: http://www.youtube.com/watch?v=Qv7Y-Er7rgc. Licencia: Dominio Público: Sin Derechos de Autor Conocidos. Términos de la licencia: Licencia estándar de YouTube
• Ángulo de Brewster. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Brewster's_Angle. Licencia: CC BY: Atribución
• Ángulo de Brewster. Proporcionado por: Wikipedia. Ubicado en: http://en.Wikipedia.org/wiki/Brewster's_angle. Licencia: CC BY: Atribución
• OpenStax College, Dispersión: El arco iris y los prismas. 29 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42466/latest/. Licencia: CC BY: Atribución
• OpenStax College, Dispersión: El arco iris y los prismas. 29 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42466/latest/. Licencia: CC BY: Atribución
• OpenStax College, Dispersión: El arco iris y los prismas. 29 de enero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42466/latest/Figure%2026_05_02.jpg. Licencia: CC BY: Atribución