8.1: Fibra Óptica- Método de Operación

En su forma más simple, la fibra óptica consiste en regiones concéntricas de material dieléctrico como se muestra en la Figura$\PageIndex{1}$.

Figura$\PageIndex{1}$: Construcción de la forma más simple de fibra óptica. (CC BY-SA 4.0; S. Lally)

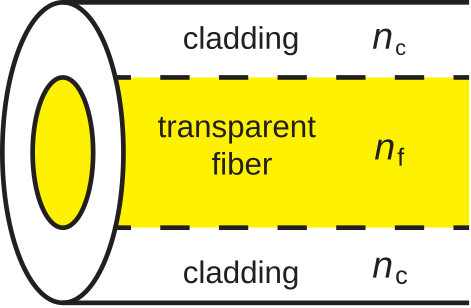
Una sección transversal a través de la fibra revela una región circular de material dieléctrico transparente a través del cual se propaga la luz. Esta está rodeada por una camisa de material dieléctrico comúnmente conocida como revestimiento.

Una característica del diseño de cualquier fibra óptica es que la permitividad de la fibra es mayor que la permitividad del revestimiento. Como se explica en la Sección 5.11, esto crea las condiciones necesarias para una reflexión interna total. El mecanismo de reflexión interna total contiene la luz dentro de la fibra.

En la disciplina de la óptica, la permitividad de un material se cuantifica comúnmente en términos de su índice de refracción. El índice de refracción es la raíz cuadrada de la permitividad relativa, y generalmente se le asigna el símbolo$n$. Así, si definimos las permitividades relativas$\epsilon_{r,f} \triangleq \epsilon_f / \epsilon_0$ para la fibra y$\epsilon_{r,c} \triangleq \epsilon_c / \epsilon_0$ para el revestimiento, entonces

$$\begin{aligned} n_f &\triangleq \sqrt{\epsilon_{r,f}} \\ n_c &\triangleq \sqrt{\epsilon_{r,c}}\end{aligned} \nonumber$$

y

$$n_f > n_c \nonumber$$

La figura$\PageIndex{2}$ ilustra la reflexión interna total en una fibra óptica. En este caso, un rayo de luz en la fibra incide en el límite con el revestimiento. Podemos tratar el rayo de luz como una onda plana uniforme. Para ver por qué, considere que las longitudes de onda ópticas oscilan entre 120 nm y 700 nm en el espacio libre. La longitud de onda es ligeramente más corta que esta en fibra; específicamente, por un factor igual a la raíz cuadrada de la permitividad relativa. La fibra es del orden de milímetros de diámetro, que es aproximadamente 4 órdenes de magnitud mayor que la longitud de onda. Así, desde la perspectiva del rayo de luz, la fibra parece ser un medio espacio ilimitado que comparte un límite plano con el revestimiento, que también parece ser un medio espacio ilimitado.

Figura$\PageIndex{2}$: Reflejo interno total en fibra óptica. (CC BY-SA 4.0; S. Lally)

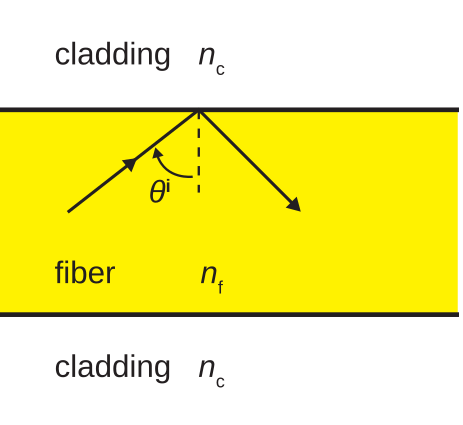
Continuando bajo esta presunción, el criterio para la reflexión interna total es (de la Sección 5.11):

$$\theta^i \ge \arcsin\sqrt{\frac{\epsilon_{r,c}}{\epsilon_{r,f}}} = \arcsin\frac{n_c}{n_f} \label{m0178_eCAnm}$$

Mientras los rayos de luz se acerquen desde ángulos que satisfagan este criterio, la potencia asociada permanece en la fibra, y se refleja hacia adelante. De lo contrario, se pierde energía en el revestimiento.

Ejemplo$\PageIndex{1}$: Critical angle for optical fiber

Los valores típicos de$n_f$ y$n_c$ para una fibra óptica son 1.52 y 1.49, respectivamente. ¿Qué ángulo interno de incidencia se requiere para mantener la reflexión interna total?

Solución

Usando la ecuación\ ref {M0178_ECANM},$\theta^i$ debe ser mayor que aproximadamente$78.8^{\circ}$. En la práctica esto es bastante razonable ya que deseamos que la luz esté viajando aproximadamente paralela al eje de la fibra ($\theta^i\approx 90^{\circ}$) de todos modos.

El criterio de reflexión interna total impone un límite en el radio de curvatura del cable de fibra óptica. Si el cable de fibra óptica se dobla de tal manera que el radio de curvatura es demasiado pequeño, el ángulo crítico se superará en la curva. Esto ocurrirá incluso para los rayos de luz que viajan perfectamente paralelos al eje de la fibra antes de que lleguen a la curva.

Tenga en cuenta que el revestimiento cumple al menos dos funciones. Primero, determina el ángulo crítico para la reflexión interna total, y posteriormente determina el radio mínimo de curvatura para el funcionamiento sin pérdidas de la fibra. En segundo lugar, proporciona un lugar para que las ondas superficiales evanescentes asociadas con la reflexión interna total (Sección 5.12) existan sin interferencia de objetos en contacto con la fibra.