Saltar al contenido principal
LibreTexts Español

4.5: Resolución de problemas

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    127963
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Un enfoque general

    Las técnicas básicas de resolución de problemas pueden ayudar en la solución de problemas que involucran el movimiento (es decir, las leyes del movimiento).

    objetivos de aprendizaje

    • Evaluar las leyes del movimiento a través de técnicas prácticas de resolución de problemas

    Cuando se trata de las leyes del movimiento, aunque el conocimiento de conceptos y ecuaciones es importante, comprender las técnicas básicas de resolución de problemas puede simplificar el proceso de resolución de problemas que pueden parecer difíciles. Su enfoque para la resolución de problemas puede implicar varios pasos clave.

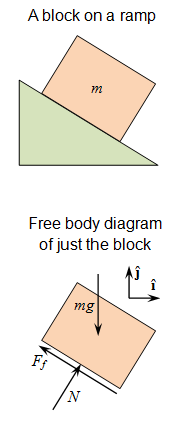
    imagen

    Diagrama de cuerpo libre: Un ejemplo de un dibujo para ayudar a identificar fuerzas y direcciones.

    Primero, reunir toda la información relevante del problema. Identificar todas las cantidades que se dan (los conocimientos), luego hacer lo mismo para todas las cantidades necesarias (las incógnitas). También, identificar los principios físicos involucrados (por ejemplo, fuerza, gravedad, fricción, etc.).

    A continuación, un dibujo puede ser útil. A veces un dibujo puede incluso ayudar a determinar las cantidades conocidas y desconocidas. No necesita ser una obra de arte, sino que debe ser lo suficientemente clara como para ilustrar la dimensión adecuada, (es decir, una, dos o tres dimensiones). A continuación, puede utilizar este dibujo para determinar qué dirección es positiva y cuál es negativa (tomando nota de esto en el dibujo).

    Un siguiente paso es usar lo que se sabe para encontrar la ecuación adecuada para encontrar lo que se desconoce. Si bien es más fácil encontrar una ecuación que deje solo una desconocida, a veces esto no es posible. En estas situaciones, puedes resolver múltiples ecuaciones para encontrar la respuesta correcta. Recuerda que las ecuaciones representan principios físicos y relaciones, así que usa las ecuaciones y dibujos en tándem.

    Luego puede sustituir los conocimientos en las ecuaciones apropiadas y encontrar una solución numérica.

    Revisa la respuesta para ver si es razonable y tiene sentido. Tu juicio va a mejorar y afinar a medida que resuelvas más problemas de esta naturaleza. Este paso de “juicio” ayuda a intuir el problema en términos de su significado conceptual. Si puedes juzgar si la respuesta es razonable, tienes una comprensión más profunda de la física que simplemente la mecánica de la resolución de problemas.

    A la hora de resolver problemas, tendemos a realizar estos pasos en diferente orden, así como a realizar varios pasos simultáneamente. No existe un procedimiento rígido que funcione cada vez. La creatividad y el conocimiento crecen con la experiencia. Con el tiempo, los conceptos básicos de la resolución de problemas pueden volverse relativamente automáticos.

    Puntos Clave

    • Recopilar toda la información relevante e identificar los conocimientos e incógnitas es un primer paso importante.
    • Siempre hacer un dibujo para ayudar a identificar direcciones de fuerzas y establecer\(\mathrm{x, y}\), y\(\mathrm{z}\) ejes.
    • Elija las ecuaciones correctas, resuelva el problema y verifique que la respuesta se ajuste numéricamente a las expectativas.

    Términos Clave

    • ecuación: Afirmación de que dos expresiones son iguales, expresadas escribiendo las dos expresiones separadas por un signo igual; a partir de la cual una es determinar una cantidad particular.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 4.5: Resolución de problemas is shared under a not declared license and was authored, remixed, and/or curated by Boundless.