1.1: Números reales - Álgebra Esencial
- Page ID
- 112014
- Clasificar un número real como un número natural, entero, entero, racional o irracional.
- Realizar cálculos usando orden de operaciones.
- Utilice las siguientes propiedades de números reales: conmutativo, asociativo, distributivo, inverso e identidad.
- Evaluar expresiones algebraicas.
- Simplifica las expresiones algebraicas.
A menudo se dice que las matemáticas son el lenguaje de la ciencia. Si esto es cierto, entonces el lenguaje de las matemáticas son los números. El primer uso de los números ocurrió hace\(100\) siglos en el Medio Oriente para contar, o enumerar artículos. Los agricultores, ganaderos y comerciantes utilizaron fichas, piedras o marcadores para indicar una sola cantidad: una gavilla de grano, una cabeza de ganado o una longitud fija de tela, por ejemplo. Hacerlo hizo posible el comercio, lo que llevó a mejorar las comunicaciones y la difusión de la civilización.
Hace tres a cuatro mil años, los egipcios introdujeron fracciones. Primero los usaron para mostrar recíprocos. Posteriormente, los utilizaron para representar la cantidad cuando una cantidad se dividía en partes iguales.
Pero, ¿y si no hubiera ganado para comerciar o una cosecha entera de grano se perdiera en una inundación? ¿Cómo podría alguien indicar la existencia de nada? Desde los primeros tiempos, la gente había pensado en un “estado base” mientras contaba y utilizaba varios símbolos para representar esta condición nula. Sin embargo, no fue hasta aproximadamente el siglo V d.C. en la India que se agregó cero al sistema numérico y se utilizó como numeral en los cálculos.
Claramente, también era necesario que los números representaran pérdida o deuda. En la India, en el siglo VII d.C., se utilizaron números negativos como soluciones a ecuaciones matemáticas y deudas comerciales. Los opuestos de los números de conteo expandieron aún más el sistema numérico.
Debido a la evolución del sistema de números, ahora podemos realizar cálculos complejos utilizando estas y otras categorías de números reales. En esta sección, exploraremos conjuntos de números, cálculos con diferentes tipos de números y el uso de números en expresiones.
Clasificar un número real
Los números que utilizamos para contar, o enumerar elementos, son los números naturales:\(1, 2, 3, 4, 5\) y así sucesivamente. Los describimos en notación fija como\(\{1,2,3,...\}\) donde los puntos suspensivos\((\cdots)\) indican que los números continúan hasta el infinito. Los números naturales son, por supuesto, también llamados los números de conteo. Cada vez que enumeramos a los miembros de un equipo, contamos las monedas de una colección o contabilizamos los árboles en una arboleda, estamos usando el conjunto de números naturales. El conjunto de números enteros es el conjunto de números naturales más cero:\(\{0,1,2,3,...\}\).
El conjunto de enteros suma los opuestos de los números naturales al conjunto de números enteros:\(\{\cdots,-3,-2,-1,0,1,2,3,\cdots\}\). Es útil señalar que el conjunto de enteros se compone de tres subconjuntos distintos: enteros negativos, cero y enteros positivos. En este sentido, los enteros positivos son solo los números naturales. Otra forma de pensarlo es que los números naturales son un subconjunto de los enteros.
\[ \overbrace{\cdots, -3,-2,-1}^{\text{negative integers}}, \underbrace{0}_{\text{zero}}, \overbrace{1,\, 2,\,3,\, \cdots}^{\text{positive integers}} \nonumber\]
El conjunto de números racionales se escribe como\(\{\frac{m}{n}| \text{m and n are integers and } n \neq 0\}\) .Observe a partir de la definición que los números racionales son fracciones (o cocientes) que contienen enteros tanto en el numerador como en el denominador, y el denominador nunca lo es\(0\). También podemos ver que cada número natural, número entero y entero es un número racional con un denominador de\(1\).
Debido a que son fracciones, cualquier número racional también se puede expresar en forma decimal. Cualquier número racional se puede representar como:
- un decimal de terminación:\(\frac{15}{8} =1.875\), o
- un decimal repetirse:\(\frac{4}{11} =0.36363636\cdots = 0.\bar{36}\)
Usamos una línea dibujada sobre el bloque repetitivo de números en lugar de escribir el grupo varias veces.
Escribe cada uno de los siguientes como un número racional. Escribe una fracción con el entero en el numerador y\(1\) in the denominator.
- \(7\)
- \(0\)
- \(-8\)
Solución
a.\(7= \frac{7}{1}\)
b.\(0= \frac{0}{1}\)
c.\(-8= \frac{-8}{1}\)
Escribe cada uno de los siguientes como un número racional.
- \(11\)
- \(3\)
- \(-4\)
- Contestar
-
- \(\frac{11}{1}\)
- \(\frac{3}{1}\)
- \(-\frac{4}{1}\)
Escribe cada uno de los siguientes números racionales como un decimal terminante o repetido.
- \(-\frac{5}{7}\)
- \(\frac{15}{5}\)
- \(\frac{13}{25}\)
Solución
a. un decimal repetido
b.\(\frac{15}{5} = 3\) (o\(3.0\)), un decimal de terminación
c.\(\frac{13}{25} =0.52\), un decimal de terminación
Escribe cada uno de los siguientes números racionales como un decimal terminante o repetido.
- \(\frac{68}{17}\)
- \(\frac{8}{13}\)
- \(-\frac{13}{25}\)
- Contestar
-
- \(4\)(o\(4.0\)), terminando
- \(0.\overline{615384}\), repitiendo
- \(-0.85\), terminando
Números irracionales
En algún momento del pasado antiguo, alguien descubrió que no todos los números son números racionales. Un constructor, por ejemplo, pudo haber encontrado que la diagonal de un cuadrado con lados unitarios no era\(2\) ni siquiera\(32\), sino que era otra cosa. O un fabricante de ropa pudo haber observado que la relación entre la circunferencia y el diámetro de un rollo de tela era un poco más que\(3\), pero aún así no un número racional. Se dice que tales números son irracionales porque no pueden escribirse como fracciones. Estos números conforman el conjunto de números irracionales. Los números irracionales no pueden expresarse como una fracción de dos enteros. Es imposible describir este conjunto de números por una sola regla excepto decir que un número es irracional si no es racional. Entonces escribimos esto como se muestra.
\[\{h\mid h \text { is not a rational number}\}\]
Determinar si cada uno de los siguientes números es racional o irracional. Si es racional, determine si se trata de un decimal de terminación o repetición.
- \(\sqrt{25}\)
- \(\frac{33}{9}\)
- \(\sqrt{11}\)
- \(\frac{17}{34}\)
- \(0.3033033303333…\)
Solución
- \(\sqrt{25}\): Esto puede simplificarse como\(\sqrt{25} = 5\) .Por lo tanto,\(\sqrt{25}\) es racional.
- \(\frac{33}{9}\): Porque es una fracción,\(\frac{33}{9}\) es un número racional. A continuación, simplificar y dividir. \[\frac{33}{9}=\cancel{\frac{33}{9}} \nonumber\]Entonces,\(\frac{33}{9}\) es racional y un decimal repetido.
- \(\sqrt{11}\): Esto no se puede simplificar más. Por lo tanto,\(\sqrt{11}\) es un número irracional.
- \(\frac{17}{34}\): Porque es una fracción,\(\frac{17}{34}\) es un número racional. Simplifique y divida. \[\frac{17}{34} = 0.5 \nonumber\]Entonces,\(\frac{17}{34}\) es racional y un decimal de terminación.
- \(0.3033033303333…\)no es un decimal de terminación. También tenga en cuenta que no hay patrón repetitivo porque el grupo de\(3s\) aumenta cada vez. Por lo tanto, no es un decimal terminante ni repetido y, por lo tanto, no es un número racional. Es un número irracional.
Determinar si cada uno de los siguientes números es racional o irracional. Si es racional, determine si se trata de un decimal de terminación o repetición.
- \(\frac{7}{77}\)
- \(\sqrt{81}\)
- \(4.27027002700027…\)
- \(\frac{91}{13}\)
- \(\sqrt{39}\)
- Contestar
-
- racional y repetitivo;
- racional y terminante;
- irracional;
- racional y terminante;
- irracional
Números Reales
Dado cualquier número\(n\), sabemos que\(n\) es o racional o irracional. No puede ser ambas cosas. Los conjuntos de números racionales e irracionales juntos conforman el conjunto de números reales. Como vimos con los números enteros, los números reales se pueden dividir en tres subconjuntos: números reales negativos, cero y números reales positivos. Cada subconjunto incluye fracciones, decimales y números irracionales según su signo algebraico (+ o —). El cero no se considera ni positivo ni negativo.
Los números reales se pueden visualizar en una recta numérica horizontal con un punto arbitrario elegido como\(0\), con números negativos a la izquierda de\(0\) y números positivos a la derecha de\(0\). Luego se usa una distancia unitaria fija para marcar cada número entero (u otro valor básico) a cada lado de\(0\). Cualquier número real corresponde a una posición única en la línea numérica. Lo contrario también es cierto: Cada ubicación en la línea numérica corresponde exactamente a un número real. Esto se conoce como correspondencia uno a uno. Nos referimos a esto como la línea numérica real como se muestra en la Figura (\(\PageIndex{1}\).

Clasificar cada número como positivo o negativo y como racional o irracional. ¿El número se encuentra a la izquierda o a la derecha de\(0\) en la recta numérica?
- \(-\frac{10}{3}\)
- \(-\sqrt{5}\)
- \(-6π\)
- \(0.615384615384…\)
Solución
- \(-\frac{10}{3}\)es negativo y racional. Se encuentra a la izquierda de\(0\) en la recta numérica.
- \(-\sqrt{5}\)es positivo e irracional. Se encuentra a la derecha de\(0\).
- \(-\sqrt{289} = -\sqrt{17^2} = -17\)es negativo y racional. Se encuentra a la izquierda de\(0\).
- \(-6π\)es negativo e irracional. Se encuentra a la izquierda de\(0\).
- \(0.615384615384…\)es un decimal repetido por lo que es racional y positivo. Se encuentra a la derecha de\(0\).
Clasificar cada número como positivo o negativo y como racional o irracional. ¿El número se encuentra a la izquierda o a la derecha de\(0\) en la recta numérica?
- \(\sqrt{73}\)
- \(-11.411411411…\)
- \(\frac{47}{19}\)
- \(-\frac{\sqrt{5}}{2}\)
- \(6.210735\)
- Contestar
-
- positivo, irracional
- derecha negativa, racional
- izquierda positiva, racional
- derecha negativa, irracional
- izquierda positiva, racional; derecha
Conjuntos de números como subconjuntos
Comenzando con los números naturales, hemos expandido cada conjunto para formar un conjunto más grande, lo que significa que existe una relación de subconjunto entre los conjuntos de números que hemos encontrado hasta ahora. Estas relaciones se vuelven más obvias cuando se ven como un diagrama, como la Figura (\(\PageIndex{2}\)).
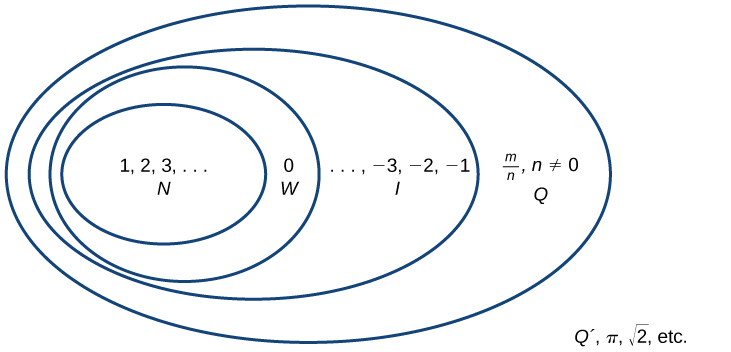
El conjunto de números naturales incluye los números utilizados para contar:\(\{1,2,3,...\}\).
El conjunto de números enteros es el conjunto de números naturales más cero:\(\{0,1,2,3,...\}\).
El conjunto de enteros suma los números naturales negativos al conjunto de números enteros:\(\{...,-3,-2,-1,0,1,2,3,...\}\).
El conjunto de números racionales incluye fracciones escritas como\(\{\frac{m}{n} | \text{m and n are integers and } n \neq 0\}\).
El conjunto de números irracionales es el conjunto de números que no son racionales, no se repiten, y no terminan:\(\{h\parallel \text{h is not a rational number}\}\).
Clasificar cada número como un número natural (N), número entero (W), entero (I), número racional (Q) y/o número irracional (Q′).
- \(\sqrt{36}\)
- \(\frac{8}{3}\)
- \(\sqrt{73}\)
- \(-6\)
- \(3.2121121112…\)
Solución
| N | W | I | Q | Q' | |
|---|---|---|---|---|---|
| a.\(\sqrt{36} = 6\) | X | X | X | X | |
| b.\(\frac{8}{3} =2.\overline{6}\) | X | ||||
| c.\(\sqrt{73}\) | X | ||||
| d.\(-6\) | X | X | |||
| e.\(3.2121121112...\) | X |
Clasificar cada número como un número natural (N), número entero (W), entero (I), número racional (Q) y/o número irracional (Q′).
- \(-\frac{35}{7}\)
- \(0\)
- \(\sqrt{169}\)
- \(\sqrt{24}\)
- \(4.763763763...\)
- Contestar
-
N W I Q Q' a.\(-\frac{35}{7}\) X X b.\(0\) X X X c.\(\sqrt{169}\) X X X X d.\(\sqrt{24}\) X e.\(4.763763763...\) X
Realización de Cálculos Usando el Orden de Operaciones
Cuando multiplicamos un número por sí mismo, lo cuadramos o lo elevamos a una potencia de\(2\). Por ejemplo,\(4^2 =4\times4=16\). Podemos elevar cualquier número a cualquier potencia. En general, la notación exponencial a significa que el número o variable\(a\) se utiliza como factor\(n\) veces.
\[a^n=a\cdot a\cdot a\cdots a \qquad \text{ n factors} \nonumber \]
En esta notación,\(a^n\) se lee como el\(n^{th}\) poder de\(a\), donde\(a\) se llama la base y\(n\) se llama el exponente. Un término en notación exponencial puede ser parte de una expresión matemática, que es una combinación de números y operaciones. Por ejemplo,\(24+6 \times \dfrac{2}{3} − 4^2\) es una expresión matemática.
Para evaluar una expresión matemática, realizamos las diversas operaciones. Sin embargo, no los realizamos en ningún orden aleatorio. Utilizamos el orden de las operaciones. Esta es una secuencia de reglas para evaluar tales expresiones.
Recordemos que en matemáticas utilizamos paréntesis (), corchetes [], y llaves {} para agrupar números y expresiones para que todo lo que aparezca dentro de los símbolos sea tratado como una unidad. Adicionalmente, las barras de fracción, los radicales y las barras de valor absoluto se tratan como símbolos de agrupación. Al evaluar una expresión matemática, comience simplificando las expresiones dentro de los símbolos de agrupación.
El siguiente paso es abordar cualquier exponente o radicales. Después, realiza multiplicación y división de izquierda a derecha y finalmente suma y resta de izquierda a derecha.
Echemos un vistazo a la expresión proporcionada.
\[24+6 \times \dfrac{2}{3} − 4^2 \nonumber\]
No hay símbolos de agrupación, así que pasamos a exponentes o radicales. El número\(4\) se eleva a una potencia de\(2\), así simplificar\(4^2\) como\(16\).
\[24+6 \times \dfrac{2}{3} − 4^2 \nonumber \]
\[24+6 \times \dfrac{2}{3} − 16 \nonumber\]
A continuación, realizar multiplicación o división, de izquierda a derecha.
\[24+6 \times \dfrac{2}{3} − 16 \nonumber\]
\[24+4-16 \nonumber\]
Por último, realizar suma o resta, de izquierda a derecha.
\[24+4−16 \nonumber\]
\[28−16 \nonumber\]
\[12 \nonumber\]
Por lo tanto,
\[24+6 \times \dfrac{2}{3} − 4^2 =12 \nonumber\]
Para algunas expresiones complicadas, se necesitarán varios pases por el orden de las operaciones. Por ejemplo, puede haber una expresión radical dentro de paréntesis que debe simplificarse antes de que se evalúen los paréntesis. Seguir el orden de las operaciones asegura que cualquiera que simplifique la misma expresión matemática obtendrá el mismo resultado.
Las operaciones en expresiones matemáticas deben evaluarse en un orden sistemático, lo que puede simplificarse usando el acrónimo PEMDAS:
- P (arentesis)
- E (xponentes)
- M (ultiplicación) y D (ivisión)
- A (ddition) y S (ubtracción)
- Simplifique cualquier expresión dentro de los símbolos de agrupación.
- Simplifica cualquier expresión que contenga exponentes o radicales.
- Realizar cualquier multiplicación y división en orden, de izquierda a derecha.
- Realizar cualquier suma y resta en orden, de izquierda a derecha.
Utilice el orden de las operaciones para evaluar cada una de las siguientes expresiones.
- \(\dfrac{5^2-4}{7}- \sqrt{11-2}\)
- \(\dfrac{14-3 \times2}{2 \times5-3^2}\)
- \(7\times(5\times3)−2\times[(6−3)−4^2]+1\)
Solución
- \[\begin{align*} (3\times2)^2-4\times(6+2)&=(6)^2-4\times(8) && \qquad \text{Simplify parentheses}\\ &=36-4\times8 && \qquad \text{Simplify exponent}\\ &=36-32 && \qquad \text{Simplify multiplication}\\ &=4 && \qquad \text{Simplify subtraction}\\ \end{align*}\]
- \[\begin{align*} \dfrac{5^2-4}{7}- \sqrt{11-2}&= \dfrac{5^2-4}{7}-\sqrt{9} && \qquad \text{Simplify grouping symbols (radical)}\\ &=\dfrac{5^2-4}{7}-3 && \qquad \text{Simplify radical}\\ &=\dfrac{25-4}{7}-3 && \qquad \text{Simplify exponent}\\ &=\dfrac{21}{7}-3 && \qquad \text{Simplify subtraction in numerator}\\ &=3-3 && \qquad \text{Simplify division}\\ &=0 && \qquad \text{Simplify subtraction} \end{align*}\]
Obsérvese que en el primer paso, el radical se trata como un símbolo de agrupación, como paréntesis. También, en el tercer paso, la barra de fracciones se considera un símbolo de agrupación por lo que se considera que el numerador está agrupado.
- \[\begin{align*} 6-\mid 5-8\mid +3\times(4-1)&=6-|-3|+3\times3 && \qquad \text{Simplify inside grouping symbols}\\ &=6-3+3\times3 && \qquad \text{Simplify absolute value}\\ &=6-3+9 && \qquad \text{Simplify multiplication}\\ &=3+9 && \qquad \text{Simplify subtraction}\\ &=12 && \qquad \text{Simplify addition}\\ \end{align*}\]
- \[\begin{align*} \dfrac{14-3 \times2}{2 \times5-3^2}&=\dfrac{14-3 \times2}{2 \times5-9} && \qquad \text{Simplify exponent}\\ &=\dfrac{14-6}{10-9} && \qquad \text{Simplify products}\\ &=\dfrac{8}{1} && \qquad \text{Simplify differences}\\ &=8 && \qquad \text{Simplify quotient}\\ \end{align*}\]
En este ejemplo, la barra de fracciones separa el numerador y el denominador, lo que simplificamos por separado hasta el último paso.
- \[\begin{align*} 7\times(5\times3)-2\times[(6-3)-4^2]+1&=7\times(15)-2\times[(3)-4^2]+1 && \qquad \text{Simplify inside parentheses}\\ &=7\times(15)-2\times(3-16)+1 && \qquad \text{Simplify exponent}\\ &=7\times(15)-2\times(-13)+1 && \qquad \text{Subtract}\\ &=105+26+1 && \qquad \text{Multiply}\\ &=132 && \qquad \text{Add} \end{align*}\]
Utilice el orden de las operaciones para evaluar cada una de las siguientes expresiones.
- \(\sqrt{5^2-4^2}+7\times(5-4)^2\)
- \(1+\dfrac{7\times5-8\times4}{9-6}\)
- \(|1.8-4.3|+0.4\times\sqrt{15+10}\)
- \(\dfrac{1}{2}\times[5\times3^2-7^2]+\dfrac{1}{3}\times9^2\)
- \([(3-8^2)-4]-(3-8)\)
- Contestar
-
- \(10\)
- \(2\)
- \(4.5\)
- \(25\)
- \(26\)
Uso de propiedades de números reales
Para algunas actividades que realizamos, el orden de ciertas operaciones no importa, pero el orden de otras operaciones sí. Por ejemplo, no hace diferencia si nos ponemos el zapato derecho antes que el izquierdo o viceversa. No obstante, sí importa si primero nos ponemos zapatos o calcetines. Lo mismo es cierto para las operaciones en matemáticas.
Propiedades conmutativas
La propiedad conmutativa de suma establece que los números se pueden sumar en cualquier orden sin afectar la suma.
\[a+b=b+a\]
Podemos ver mejor esta relación al usar números reales.
\((−2)+7 = 5 \text{ and } 7+(−2)=5\)
De igual manera, la propiedad conmutativa de la multiplicación establece que los números pueden multiplicarse en cualquier orden sin afectar al producto.
\[a\times b=b\times a\]
De nuevo, consideremos un ejemplo con números reales.
Es importante señalar que ni la resta ni la división son conmutativas. Por ejemplo, no\(17−5\) es lo mismo que\(5−17\). De igual manera,\(20÷5≠5÷20\).
Propiedades asociativas
La propiedad asociativa de la multiplicación nos dice que no importa cómo agrupemos los números a la hora de multiplicar. Podemos mover los símbolos de agrupación para facilitar el cálculo, y el producto sigue siendo el mismo.
\[a(bc)=(ab)c\]
Considera este ejemplo.
\((3\times4)\times5=60 \text{ and } 3\times(4\times5)=60\)
La propiedad asociativa de suma nos dice que los números pueden agruparse de manera diferente sin afectar a la suma.
\[a+(b+c)=(a+b)+c\]
Esta propiedad puede ser especialmente útil cuando se trata de enteros negativos. Considera este ejemplo.
\([15+(−9)]+23=29 \text{ and } 15+[(−9)+23]=29\)
¿La resta y la división son asociativas? Revisa estos ejemplos.
\[\begin{align*} 8-(3-15)\overset{?}{=}&(8-3)-15\\ 8-(-12)\overset{?}{=}&5-15\\ 20 \neq &10\\ 64\div (8\div 4)\overset{?}{=}&(64\div 8)\div 4\\ 64\div 2\overset{?}{=}&8\div 4\\ 32 \neq & 2 \end{align*}\]
Como podemos ver, ni la resta ni la división son asociativas.
Propiedad distributiva
La propiedad distributiva establece que el producto de un factor por una suma es la suma del factor por cada término en la suma.
\[a\times(b+c)=a\times b+a\times c\]
Esta propiedad combina tanto suma como multiplicación (y es la única propiedad que lo hace). Consideremos un ejemplo.
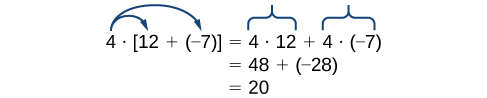
Tenga en cuenta que\(4\) is outside the grouping symbols, so we distribute the \(4\) by multiplying it by \(12\), multiplying it by \(–7\), and adding the products.
To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.
\[\begin{align*} 6+(3\times5)\overset{?}{=}&(6+3)\times(6\times5)\\ 6+(15)\overset{?}{=}&(9)\times(11)\\ 21 \neq &99 \end{align*}\]
Multiplication does not distribute over subtraction, and division distributes over neither addition nor subtraction.
A special case of the distributive property occurs when a sum of terms is subtracted.
\[a−b=a+(−b)\]
For example, consider the difference \(12−(5+3)\). We can rewrite the difference of the two terms \(12\) and \((5+3)\) by turning the subtraction expression into addition of the opposite. So instead of subtracting \( (5+3)\), we add the opposite.
Now, distribute \(-1\) and simplify the result.
\[\begin{align*} 12-(5+3)&=12+(-1)\times(5+3)\\ &=12+[(-1)\times5+(-1)\times3]\\ &=12+(-8)\\ &=4 \end{align*}\]
This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.
\[\begin{align*} 12-(5+3)&=12+(-5-3)\\ &=12-8\\ &=4 \end{align*}\]
Identity Properties
The identity property of addition states that there is a unique number, called the additive identity \((0)\) that, when added to a number, results in the original number.
\[a+0=a\]
The identity property of multiplication states that there is a unique number, called the multiplicative identity \((1)\) that, when multiplied by a number, results in the original number.
\[a\times 1=a\]
For example, we have \( (−6)+0=−6\) and\( 23\times1=23\). There are no exceptions for these properties; they work for every real number, including \(0\) and \(1\).
Inverse Properties
The inverse property of addition states that, for every real number a, there is a unique number, called the additive inverse (or opposite), denoted \(−a\), that, when added to the original number, results in the additive identity, \(0\).
\[a+(−a)=0\]
For example, if \(a =−8\), the additive inverse is \(8\), since \((−8)+8=0\).
The inverse property of multiplication holds for all real numbers except \(0\) because the reciprocal of \(0\) is not defined. The property states that, for every real number \(a\), there is a unique number, called the multiplicative inverse (or reciprocal), denoted \(1a\), that, when multiplied by the original number, results in the multiplicative identity, \(1\).
\[a\times \dfrac{1}{a}=1\]
For example, if \(a =−\dfrac{2}{3}\), the reciprocal, denoted \(\dfrac{1}{a}\), is \(-\dfrac{3}{2}\) because
\[a⋅\dfrac{1}{a}=\left(−\dfrac{2}{3}\right)\times\left(−\dfrac{3}{2}\right)=1 \nonumber\]
The following properties hold for real numbers \(a\), \(b\), and \(c\).
| Addition | Multiplication | |
|---|---|---|
| Commutative Property | \(a+b=b+a\) | \(a\times b=b\times a\) |
| Associative Property | \(a+(b+c)=(a+b)+c\) | \(a(bc)=(ab)c\) |
| Distributive Property | \(a\times (b+c)=a\times b+a\times c\) | |
| Identity Property |
There exists a unique real number called the additive identity, 0, such that, for any real number a \(a+0=a\)
|
There exists a unique real number called the multiplicative identity, 1, such that, for any real number a \(a\times 1=a\)
|
| Inverse Property |
Every real number a has an additive inverse, or opposite, denoted –a, such that \(a+(−a)=0\)
|
Every nonzero real number a has a multiplicative inverse, or reciprocal, denoted 1a , such that \(a\times \left(\dfrac{1}{a}\right)=1\)
|
Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.
- \(3\times 6+3\times 4\)
- \((5+8)+(−8)\)
- \(6−(15+9)\)
- \(\dfrac{4}{7}\times\left(\dfrac{2}{3}\times \dfrac{7}{4}\right)\)
- \(100\times[0.75+(−2.38)]\)
Solution
- \[\begin{align*} 3\times6+3\times4&=3\times(6+4)\qquad \text{Distributive property}\\ &=3\times10\qquad \text{Simplify}\\ &=30\qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} (5+8)+(-8)&=5+[8+(-8)]\qquad \text{Associative property of addition}\\ &=5+0\qquad \text{Inverse property of addition}\\ &=5\qquad \text{Identity property of addition}\\ \end{align*}\]
- \[\begin{align*} 6-(15+9)&=6+[(-15)+(-9)]\qquad \text{Distributive property}\\ &=6+(-24)\qquad \text{Simplify}\\ &=-18\qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} \dfrac{4}{7}\times\left(\dfrac{2}{3}\times\dfrac{7}{4}\right)&=\dfrac{4}{7}\times\left(\dfrac{7}{4}\times\dfrac{2}{3}\right)\qquad \text{Commutative property of multiplication}\\ &=\left(\dfrac{4}{7}\times\dfrac{7}{4}\right)\times\dfrac{2}{3}\qquad \text{Associative property of multiplication}\\ &=1\times\dfrac{2}{3}\qquad \text{Inverse property of multiplication}\\ &=\dfrac{2}{3}\qquad \text{Identity property of multiplication}\\ \end{align*}\]
- \[\begin{align*} 100\times[0.75+(-2.38)]&=100\times0.75+100\times(-2.38)\qquad \text{Distributive property}\\ &=75+(-238)\qquad \text{Simplify}\\ &=-163\qquad \text{Simplify} \end{align*}\]
Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.
- \(\left(-\dfrac{23}{5}\right)\times\left[11\times\left(-\dfrac{5}{23}\right)\right]\)
- \(5\times(6.2+0.4)\)
- \(18-(7-15)\)
- \(\dfrac{17}{18}+\left[\dfrac{4}{9}+\left(-\dfrac{17}{18}\right)\right]\)
- \(6\times(-3)+6\times3\)
- Answer
-
- \(11)\), commutative property of multiplication
- \(33\), distributive property
- \(26\), distributive property
- \(\dfrac{4}{9}\), commutative property of addition, associative property of addition, inverse property of addition, identity property of addition
- \(0\), distributive property, inverse property of addition, identity property of addition
Evaluating Algebraic Expressions
So far, the mathematical expressions we have seen have involved real numbers only. In mathematics, we may see expressions such as \(x +5\), \(\dfrac{4}{3}\pi r^3\), or \(\sqrt{2m^3 n^2}\). In the expression \(x +5\), \(5\) is called a constant because it does not vary and \(x\) is called a variable because it does. (In naming the variable, ignore any exponents or radicals containing the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.
We have already seen some real number examples of exponential notation, a shorthand method of writing products of the same factor. When variables are used, the constants and variables are treated the same way.
\[\begin{align*} (-3)^5 &=(-3)\times(-3)\times(-3)\times(-3)\times(-3)\Rightarrow x^5=x\times x\times x\times x\times x\\ (2\times7)^3&=(2\times7)\times(2\times7)\times(2\times7)\qquad \; \; \Rightarrow (yz)^3=(yz)\times(yz)\times(yz) \end{align*}\]
In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.
Any variable in an algebraic expression may take on or be assigned different values. When that happens, the value of the algebraic expression changes. To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression as before.
List the constants and variables for each algebraic expression.
- \(x + 5\)
- \(\dfrac{4}{3}\pi r^3\)
- \(\sqrt{2m^3 n^2}\)
Solution
| Constants | Variables | |
|---|---|---|
| a. \(x + 5\) | \(5\) | \(x\) |
| b. \(\dfrac{4}{3}\pi r^3\) | \(\dfrac{4}{3}\), \(\pi\) | \(r\) |
| c. \(\sqrt{2m^3 n^2}\) | \(2\) | \(m\),\(n\) |
List the constants and variables for each algebraic expression.
- \(2(L + W)\)
- \(4y^3+y\)
- Answer
-
Constants Variables a. \(2\pi r(r+h)\) \(2\),\(\pi\) \(r\),\(h\) b. \(2(L + W)\) \(2\) \(L\), \(W\) c. \(4y^3+y\) \(4\) \(y\)
Evaluate the expression \(2x−7\) for each value for \(x\).
- \(x=0\)
- \(x=1\)
- \(x=12\)
- \(x=−4\)
Solution
- Substitute \(0\) for \(x\). \[\begin{align*} 2x-7 &= 2(0)-7 \\ &= 0-7\\ &= -7\\ \end{align*}\]
- Substitute \(1\) for \(x\). \[\begin{align*} 2x-7 &= 2(1)-7 \\ &= 2-7\\ &= -5\\ \end{align*}\]
- Substitute \(\dfrac{1}{2}\) for \(x\). \[\begin{align*} 2x-7 &= 2\left (\dfrac{1}{2} \right )-7 \\ &= 1-7\\ &= -6\\ \end{align*}\]
- Substitute \(-4\) for \(x\). \[\begin{align*} 2x-7 &= 2(-4)-7 \\ &= -8-7\\ &= -15\\ \end{align*}\]
Evaluate the expression \(11−3y\) for each value for \(y\).
- \(y=2\)
- \(y=0\)
- \(y=\dfrac{2}{3}\)
- \(y=−5\)
- Answer
-
- \(11\)
- \(26\)
Evaluate each expression for the given values.
- \(x+5\) for \(x=-5\)
- \(\dfrac{t}{2t-1}\) for \(t=10\)
- \(\dfrac{4}{3}\pi r^3\) for \(r=5\)
- \(a+ab+b\) for \(a=11\), \(b=-8\)
- \(\sqrt{2m^3 n^2}\) for \(m=2\), \(n=3\)
Solution
- Substitute
\(-5\) for \(x\). \[\begin{align*} x+5 &= (-5)+5 \\ &= 0\\ \end{align*}\] - Substitute \(10\) for \(t\). \[\begin{align*} \dfrac{t}{2t-1} &= \dfrac{(10)}{2(10)-1} \\ &= \dfrac{10}{20-1}\\ &= \dfrac{10}{19}\\ \end{align*}\]
- Substitute \(5\) for \(r\)
. \[\begin{align*} \dfrac{4}{3} \pi r^3 &= \dfrac{4}{3}\pi (5)^3 \\ &= \dfrac{4}{3}\pi (125)\\ &= \dfrac{500}{3}\pi\\ \end{align*}\] - Substitute \(11\) for \(a\) and \(-8\) for \(b\)
. \[\begin{align*} a+ab+b &= (11)+(11)(-8)+(-8) \\ &= 11-88-8 \\ &= -85\\ \end{align*}\] - Substitute \(2\) for \(m\) and \(3\) for \(n\). \[\begin{align*} \sqrt{2m^3 n^2} &= \sqrt{2(2)^3 (3)^2} \\ &= \sqrt{2(8)(9)} \\ &= \sqrt{144} \\ &= 12 \end{align*}\]
Evaluate each expression for the given values.
- \(\dfrac{y+3}{y-3}\) for \(y=5\)
- \(7-2t\) for \(t=-2\)
- \(\dfrac{1}{3}\pi r^2\) for \(r=11\)
- \((p^2 q)^3\) for \(p=-2\), \(q=3\)
- \(4(m-n)-5(n-m)\) for \(m=\dfrac{2}{3}\) \(n=\dfrac{1}{3}\)
- Answer
-
- \(4\)
- \(11\)
- \(\dfrac{121}{3}\pi\)
- \(1728\)
- \(3\)
Formulas
An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation \(2x +1= 7\) has the unique solution of \(3\) because when we substitute \(3\) for \(x\) in the equation, we obtain the true statement \(2(3)+1=7\).
A formula is an equation expressing a relationship between constant and variable quantities. Very often, the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area \(A\) of a circle in terms of the radius \(r\) of the circle: \( A= \pi r^2\). For any value of \(r\), the area \(A\) can be found by evaluating the expression \(\pi r^2\).
A right circular cylinder with radius \(r\) and height \(h\) has the surface area \(S\) (in square units) given by the formula \(S=2\pi r(r+h)\). See Figure \(\PageIndex{3}\). Find the surface area of a cylinder with radius \(6\) in. and height \(9\) in. Leave the answer in terms of \(\pi\).
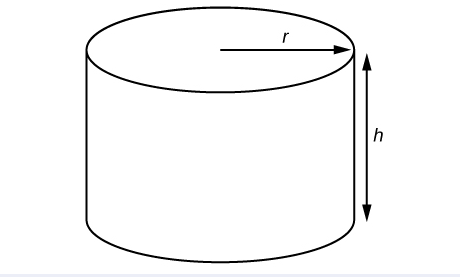
Evaluate the expression \(2\pi r(r+h)\) for \(r=6\) and \(h=9\).
Solution
\[\begin{align*} S &= 2\pi r(r+h) \\ &= 2\pi (6)[(6)+(9)] \\ &= 2\pi(6)(15) \\ &= 180\pi \end{align*}\]
The surface area is \(180\pi\) square inches.
A photograph with length \(L\) and width \(W\) is placed in a matte of width \(8\) centimeters (cm). The area of the matte (in square centimeters, or \(cm^2\) is found to be \(A=(L+16)(W+16) - L\)⋅W
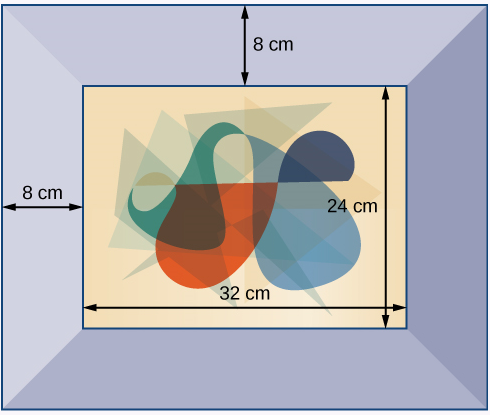
- Answer
-
\(1152cm^2\)
Simplifying Algebraic Expressions
Sometimes we can simplify an algebraic expression to make it easier to evaluate or to use in some other way. To do so, we use the properties of real numbers. We can use the same properties in formulas because they contain algebraic expressions.
Simplify each algebraic expression.
- \(3x-2y+x-3y-7\)
- \(2r-5(3-r)+4\)
- \(\left(4t-\dfrac{5}{4}s\right)-\left(\dfrac{2}{3}t+2s\right)\)
- \(2mn-5m+3mn+n\)
Solution
- \[\begin{align*} 3x-2y+x-3y-7&=3x+x-2y-3y-7 && \qquad \text{Commutative property of addition}\\ &=4x-5y-7 && \qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} 2r-5(3-r)+4&=2r-15+5r+4 && \qquad \qquad \qquad \text {Distributive property}\\ &=2r+5y-15+4 && \qquad \qquad \qquad \text{Commutative property of addition}\\ &=7r-11 && \qquad \qquad \qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} \left(4t-\dfrac{5}{4}s\right)-\left(\dfrac{2}{3}t+2s\right)&=4t-\dfrac{5}{4}s-\dfrac{2}{3}t-2s && \qquad \text{Distributive property}\\ &=4t-\dfrac{2}{3}t-\dfrac{5}{4}s-2s && \qquad \text{Commutative property of addition}\\ &=\dfrac{10}{3}t-\dfrac{13}{4}s && \qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} 2mn-5m+3mn+n&=2mn+3mn-5m+n && \qquad \text{Commutative property of addition}\\ &=5mn-5m+n && \qquad \text{Simplify}\\ \end{align*}\]
Simplify each algebraic expression.
- \(\dfrac{2}{3}y−2\left(\dfrac{4}{3}y+z\right)\)
- \(\dfrac{5}{t}−2−\dfrac{3}{t}+1\)
- \(4p(q−1)+q(1−p)\)
- \(9r−(s+2r)+(6−s)\)
- Answer
-
- \(−2y−2z\) or \(−2(y+z)\)
- \(\dfrac{2}{t}−1\)
- \(3pq−4p+q\)
- \(7r−2s+6\)
A rectangle with length \(L\) and width \(W\) has a perimeter \(P\) given by \(P =L+W+L+W\). Simplify this expression.
Solution
\[\begin{align*} P &=L+W+L+W\\ P &=L+L+W+W && \qquad \text{Commutative property of addition}\\ P &=2L+2W && \qquad \text{Simplify}\\ P &=2(L+W) && \qquad \text{Distributive property} \end{align*}\]
If the amount \(P\) is deposited into an account paying simple interest \(r\) for time \(t\), the total value of the deposit \(A\) is given by \(A =P+Prt\). Simplify the expression. (This formula will be explored in more detail later in the course.)
- Answer
-
\(A=P(1+rt)\)
Access these online resources for additional instruction and practice with real numbers.
Key Concepts
- Rational numbers may be written as fractions or terminating or repeating decimals. See Example and Example.
- Determine whether a number is rational or irrational by writing it as a decimal. See Example.
- The rational numbers and irrational numbers make up the set of real numbers. See Example. A number can be classified as natural, whole, integer, rational, or irrational. See Example.
- The order of operations is used to evaluate expressions. See Example.
- The real numbers under the operations of addition and multiplication obey basic rules, known as the properties of real numbers. These are the commutative properties, the associative properties, the distributive property, the identity properties, and the inverse properties. See Example.
- Algebraic expressions are composed of constants and variables that are combined using addition, subtraction, multiplication, and division. See Example. They take on a numerical value when evaluated by replacing variables with constants. See Example,Example, and Example
- Formulas are equations in which one quantity is represented in terms of other quantities. They may be simplified or evaluated as any mathematical expression. See Example and Example.
Glossary
- algebraic expression
- constants and variables combined using addition, subtraction, multiplication, and division
- associative property of addition
- the sum of three numbers may be grouped differently without affecting the result; in symbols,a+(b+c)=(a+b)+c
- associative property of multiplication
- the product of three numbers may be grouped differently without affecting the result; in symbols,a⋅(b⋅c)=(a⋅b)⋅c
- base
- in exponential notation, the expression that is being multiplied
- commutative property of addition
- two numbers may be added in either order without affecting the result; in symbols,a+b=b+a
- commutative property of multiplication
- two numbers may be multiplied in any order without affecting the result; in symbols,a⋅b=b⋅a
- constant
- a quantity that does not change value
- distributive property
- the product of a factor times a sum is the sum of the factor times each term in the sum; in symbols,a⋅(b+c)=a⋅b+a⋅c
- equation
- a mathematical statement indicating that two expressions are equal
- exponent
- in exponential notation, the raised number or variable that indicates how many times the base is being multiplied
- exponential notation
- a shorthand method of writing products of the same factor
- formula
- an equation expressing a relationship between constant and variable quantities
- identity property of addition
- there is a unique number, called the additive identity, 0, which, when added to a number, results in the original number; in symbols,a+0=a
- identity property of multiplication
- there is a unique number, called the multiplicative identity, 1, which, when multiplied by a number, results in the original number; in symbols,a⋅1=a
- integers
- the set consisting of the natural numbers, their opposites, and 0:{…,−3,−2,−1,0,1,2,3,…}
- inverse property of addition
- for every real numbera,there is a unique number, called the additive inverse (or opposite), denoted−a,which, when added to the original number, results in the additive identity, 0; in symbols,a+(−a)=0
- inverse property of multiplication
- for every non-zero real numbera,there is a unique number, called the multiplicative inverse (or reciprocal), denoted1a,which, when multiplied by the original number, results in the multiplicative identity, 1; in symbols,a⋅1a=1
- irrational numbers
- the set of all numbers that are not rational; they cannot be written as either a terminating or repeating decimal; they cannot be expressed as a fraction of two integers
- natural numbers
- the set of counting numbers:{1,2,3,…}
- order of operations
- a set of rules governing how mathematical expressions are to be evaluated, assigning priorities to operations
- rational numbers
- the set of all numbers of the formmn,wheremandnare integers andn≠0.Any rational number may be written as a fraction or a terminating or repeating decimal.
- real number line
- a horizontal line used to represent the real numbers. An arbitrary fixed point is chosen to represent 0; positive numbers lie to the right of 0 and negative numbers to the left.
- real numbers
- the sets of rational numbers and irrational numbers taken together
- variable
- a quantity that may change value
- whole numbers
- the set consisting of 0 plus the natural numbers:{0,1,2,3,…}


