5.6: Leyes de Kepler

Primera Ley de Kepler

La primera ley de Kepler es: La órbita de cada planeta es una elipse con el Sol en uno de los dos focos.

objetivos de aprendizaje

• Aplicar la primera ley de Kepler para describir el movimiento planetario

Primera Ley de Kepler

La primera ley de Kepler establece que

Definición

La órbita de cada planeta es una elipse con el Sol en uno de los dos focos.

Una elipse es una curva plana cerrada que se asemeja a un círculo estirado. Tenga en cuenta que el Sol no está en el centro de la elipse, sino en uno de sus focos. El otro punto focal,\(\mathrm{f_2}\), no tiene significación física para la órbita. El centro de una elipse es el punto medio del segmento de línea que une sus puntos focales. Un círculo es un caso especial de elipse donde ambos puntos focales coinciden.

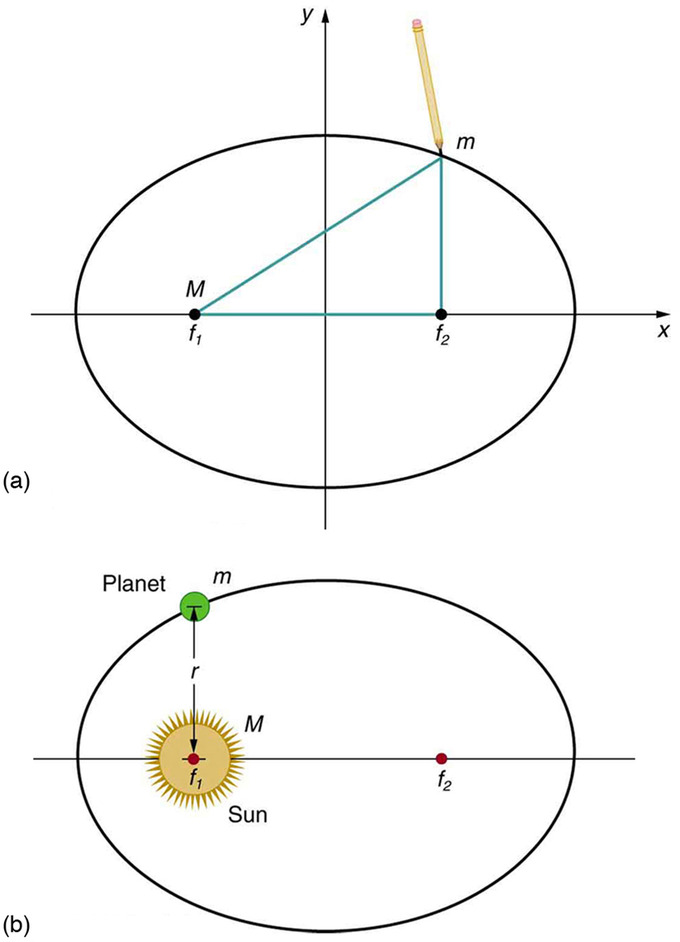
Elipses y Primera Ley de Kepler: (a) Una elipse es una curva cerrada tal que la suma de las distancias desde un punto en la curva a los dos focos (\(\mathrm{f_1}\)y\(\mathrm{f_2}\)) es una constante. Puedes dibujar una elipse como se muestra poniendo un alfiler en cada foco, y luego colocando una cuerda alrededor de un lápiz y los alfileres y trazando una línea en papel. Un círculo es un caso especial de una elipse en la que coinciden los dos focos (así cualquier punto del círculo está a la misma distancia del centro). b) Para cualquier órbita gravitacional cerrada,\(\mathrm{m}\) sigue una trayectoria elíptica con\(\mathrm{M}\) un foco. La primera ley de Kepler establece este hecho para los planetas que orbitan el Sol.

Cuán estirada está una elipse a partir de un círculo perfecto se conoce como su excentricidad: un parámetro que puede tomar cualquier valor mayor o igual a 0 (un círculo) e inferior a 1 (como la excentricidad tiende a 1, la elipse tiende a una parábola). Las excentricidades de los planetas conocidos por Kepler variaron de 0.007 (Venus) a 0.2 (Mercurio). Cuerpos menores como cometas y asteroides (descubiertos después de la época de Kepler) pueden tener excentricidades muy grandes. El planeta enano Plutón, descubierto en 1929, tiene una excentricidad de 0.25.

Simbólicamente, una elipse se puede representar en coordenadas polares como:

\[\mathrm{r=\dfrac{p}{1+ϵ \cos ⁡θ}}\]

donde\(\mathrm{(r,θ)}\) están las coordenadas polares (desde el foco) para la elipse,\(\mathrm{p}\) es el recto semilatoso, y\(\mathrm{ϵ}\) es la excentricidad de la elipse. Para un planeta que orbita al Sol,\(\mathrm{r}\) es la distancia del Sol al planeta y\(\mathrm{θ}\) es el ángulo entre la posición actual del planeta y su aproximación más cercana, con el Sol como vértice.

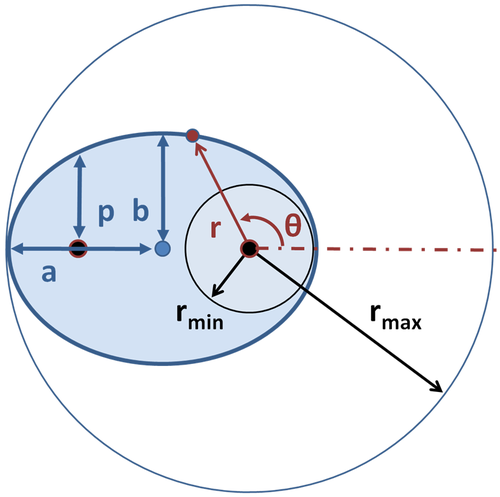
Orbit As Ellipse: Sistema de coordenadas heliocéntricas\(\mathrm{(r,θ)}\) para elipse. También se muestran: semieje mayor\(\mathrm{a}\), semieje menor\(\mathrm{b}\) y recto semilatoso\(\mathrm{p}\); centro de elipse y sus dos focos marcados por grandes puntos. Para\(\mathrm{θ=0°}\),\(\mathrm{r=r_{min}}\) y para\(\mathrm{θ=180°}\),\(\mathrm{r=r_{max}}\).

En\(\mathrm{θ=0°}\), perihelio, la distancia es mínima

\[\mathrm{r_{min}=\dfrac{p}{1+ϵ}.}\]

En\(\mathrm{θ=90°}\) y en\(\mathrm{θ=270°}\), la distancia es\(\mathrm{p}\).

En\(\mathrm{θ=180°}\), afelio, la distancia es máxima

\[\mathrm{r_{max}=\dfrac{p}{1−ϵ}.}\]

El semieje mayor\(\mathrm{a}\) es la media aritmética entre\(\mathrm{r_{min}}\) y\(\mathrm{r_{max}}\):

\[\mathrm{r_{max}−a=a−r_{min}}\]

\[\mathrm{a=\dfrac{p}{1−ϵ^2}.}\]

El eje semi-menor\(\mathrm{b}\) es la media geométrica entre\(\mathrm{r_{min}}\) y\(\mathrm{r_{max}}\):

\[\mathrm{\dfrac{r_{max}}{b}=\dfrac{b}{r_{min}}}\]

\[\mathrm{b=\dfrac{p}{\sqrt{1−ϵ^2}}}\]

El recto semilatoso\(\mathrm{p}\) es la media armónica entre\(\mathrm{r_{min}}\) y\(\mathrm{r_{max}}\):

\[\mathrm{\dfrac{1}{r_{min}}−\dfrac{1}{p}=\dfrac{1}{p}−\dfrac{1}{r_{max}}}\]

\[\mathrm{pa=r_{max}⋅r_{min}=b^2.}\]

La excentricidad\(\mathrm{ϵ}\) es el coeficiente de variación entre\(\mathrm{r_{min}}\) y\(\mathrm{r_{max}}\):

\[\mathrm{ϵ=\dfrac{r_{max}−r_{min}}{r_{max}+r_{min}}}\]

El área de la elipse es

\[\mathrm{A=πab}\]

El caso especial de un círculo es\(\mathrm{ϵ=0}\), resultando en\(\mathrm{r=p=r_{min}=r_{max}=a=b}\) y\(\mathrm{A=πr^2}\). Las órbitas de planetas con excentricidades muy pequeñas pueden aproximarse como círculos.

Comprender las 3 leyes y órbitas de Kepler: En este video se te presentarán las 3 leyes de Kepler y verás cómo son relevantes para los objetos orbitantes.

Segunda Ley de Kepler

La segunda ley de Kepler establece: Una línea que une un planeta y el Sol barre áreas iguales durante intervalos de tiempo iguales.

objetivos de aprendizaje

• Aplica la segunda ley de Kepler para describir el movimiento planetario

La segunda ley de Kepler establece:

Definición

Una línea que une un planeta y el Sol barre áreas iguales durante intervalos de tiempo iguales.

Comprender las 3 leyes y órbitas de Kepler: En este video se te presentarán las 3 leyes de Kepler y verás cómo son relevantes para los objetos orbitantes.

En poco tiempo el planeta barre un pequeño triángulo que tiene línea base y altura. El área de este triángulo viene dada por:

\[\mathrm{dA=\frac{1}{2}⋅r⋅rdθ}\]

y así la velocidad de área constante es:

\[\mathrm{\dfrac{dA}{dt}=\dfrac{1}{2}r^2\dfrac{dθ}{dt}}\]

Ahora como la primera ley establece que el planeta sigue una elipse, el planeta se encuentra a diferentes distancias del Sol en diferentes partes de su órbita. Por lo que el planeta tiene que moverse más rápido cuando está más cerca del Sol para que barre áreas iguales en tiempos iguales.

El área total encerrada por la órbita elíptica es:

\[\mathrm{A=πab}\]

Por lo tanto, el periodo\(\mathrm{P}\) satisface:

\[\mathrm{πab=P⋅\dfrac{1}{2}r^2 \dot{θ} \text{ or } r^2 \dot{θ}=nab}\]

Dónde\(\mathrm{\dot{θ}=\frac{dθ}{dt}}\) está la velocidad angular, (usando la notación Newton para la diferenciación), y\(\mathrm{n=\frac{2π}{P}}\) es el movimiento medio del planeta alrededor del Sol.

Vea a continuación una ilustración de este efecto. El planeta recorre la distancia entre A y B, C y D, y E y F en tiempos iguales. Cuando el planeta está cerca del Sol tiene una velocidad mayor, haciendo que la base del triángulo sea más grande, pero la altura del triángulo menor, que cuando el planeta está lejos del Sol. Se puede ver que el planeta viajará más rápido en el perihelio y más lento en el afelio.

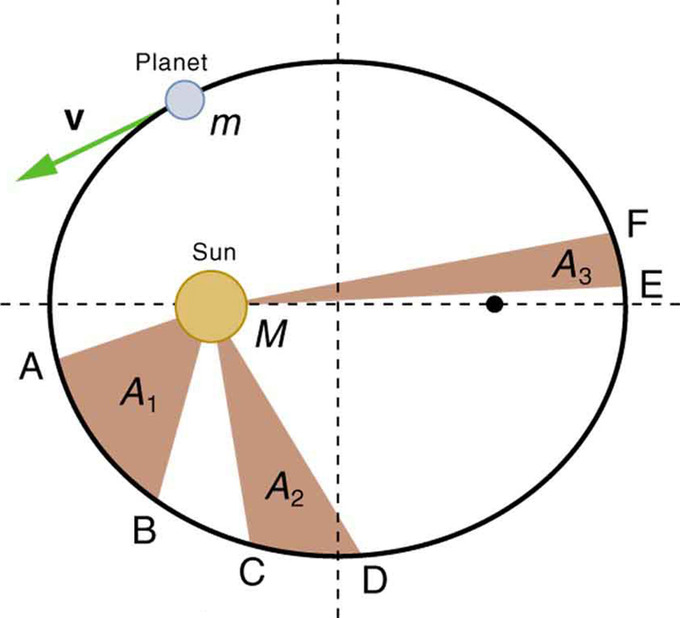
Segunda Ley de Kepler: Las regiones sombreadas tienen áreas iguales. Se necesitan tiempos iguales para que m pase de A a B, de C a D, y de E a F. La masa m se mueve más rápido cuando está más cerca de la segunda ley de M. Kepler fue ideada originalmente para planetas que orbitan el Sol, pero tiene una validez más amplia.

Tercera Ley de Kepler

La tercera ley de Kepler establece que el cuadrado del periodo orbital de un planeta es directamente proporcional al cubo del semieje mayor de su órbita.

objetivos de aprendizaje

• Aplicar la tercera ley de Kepler para describir el movimiento planetario

Tercera Ley de Kepler

La tercera ley de Kepler establece:

Definición

El cuadrado del periodo orbital de un planeta es directamente proporcional al cubo del semieje mayor de su órbita.

La tercera ley, publicada por Kepler en 1619, captura la relación entre la distancia de los planetas al Sol, y sus períodos orbitales. Simbólicamente, la ley puede expresarse como

\[\mathrm{P^2∝a^3,}\]

donde P es el periodo orbital del planeta y a es el semieje mayor de la órbita (ver).

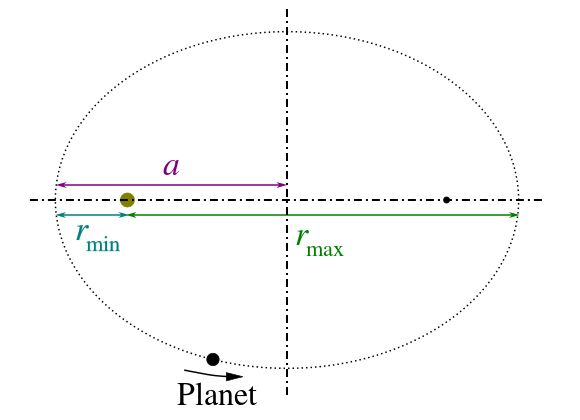
Tercera Ley de Kepler: La tercera ley de Kepler establece que el cuadrado del periodo de la órbita de un planeta alrededor del Sol es proporcional al cubo del semieje mayor de la órbita.

La constante de proporcionalidad es

\[\mathrm{\dfrac{P_{planet}^2}{a_{planet}^3}=\dfrac{P_{earth}^2}{a_{earth}^3}=1\dfrac{yr^2}{AU^3}}\]

por un año sideral (año), y unidad astronómica (AU).

Kepler enunció esta tercera ley en un laborioso intento de determinar lo que veía como la “música de las esferas” de acuerdo con leyes precisas, y expresarlo en términos de notación musical. Por lo tanto, solía conocerse como la ley armónica.

Derivación de la Tercera Ley de Kepler

Podemos derivar la tercera ley de Kepler comenzando con las leyes del movimiento de Newton y la ley universal de la gravitación. Por lo tanto, podemos demostrar que la fuerza de la gravedad es la causa de las leyes de Kepler.

Considerar una órbita circular de una masa pequeña m alrededor de una masa grande M. La gravedad suministra la fuerza centrípeta a la masa m. Comenzando con la segunda ley de Newton aplicada al movimiento circular,

\[\mathrm{F_{net}=ma_c=m\dfrac{v^2}{r}.}\]

La fuerza externa neta sobre la masa m es la gravedad, por lo que sustituimos la fuerza de gravedad por F _net:

\[\mathrm{G\dfrac{mM}{r^2}=m\dfrac{v^2}{r}}\]

La masa m cancela, así como una r, cediendo

\[\mathrm{G\dfrac{M}{r}=v^2}\]

El hecho de que m cancele es otro aspecto del hecho frecuentemente señalado de que en un lugar dado todas las masas caen con la misma aceleración. Aquí vemos que a un radio orbital dado r, todas las masas orbitan a la misma velocidad. Esto estuvo implícito por el resultado del ejemplo trabajado anterior. Ahora, para llegar a la tercera ley de Kepler, debemos meter el periodo P en la ecuación. Por definición, el periodo P es el tiempo para una órbita completa. Ahora la velocidad promedio v es la circunferencia dividida por el período, es decir,

\[\mathrm{v=\dfrac{2πr}{P}.}\]

Sustituyendo esto en la ecuación anterior da

\[\mathrm{G\dfrac{M}{r}=\dfrac{4πr^2}{P^2}}\]

Resolviendo para rendimientos de P ²

\[\mathrm{P^2=\dfrac{4π^2a^3}{GM}.}\]

El uso de los subíndices 1 y 2 para denotar dos satélites diferentes, y tomar la relación de la última ecuación para el satélite 1 al satélite 2 rinde

\[\mathrm{\dfrac{P^2_1}{P^2_2}=\dfrac{r^3_1}{r^3_2}}\]

Esta es la tercera ley de Kepler. Tenga en cuenta que la tercera ley de Kepler es válida solo para comparar satélites del mismo cuerpo padre, porque solo entonces se cancela la masa del cuerpo padre M.

Ahora considera lo que uno obtendría al resolver\(\mathrm{P^2=\frac{4π^2GM}{r^3}}\) para la proporción\(\mathrm{\frac{r^3}{P^2}}\). Obtenemos una relación que puede ser utilizada para determinar la masa M de un cuerpo padre a partir de las órbitas de sus satélites:

\[\mathrm{M=\dfrac{4π^2r^3}{GP^2}}\]

Si se conocen r y P para un satélite, entonces se puede calcular la masa M del padre. Este principio ha sido ampliamente utilizado para encontrar las masas de cuerpos celestes que tienen satélites. Además, la relación\(\mathrm{\frac{r^3}{T^2}}\) debe ser una constante para todos los satélites del mismo cuerpo padre (porque\(\mathrm{\frac{r^3}{T^2}=\frac{GM}{4π^2}}\)).

Comprender las 3 leyes y órbitas de Kepler: En este video se te presentarán las 3 leyes de Kepler y verás cómo son relevantes para los objetos orbitantes.

Maniobras orbitales

Una maniobra orbital es el uso de sistemas de propulsión para cambiar la órbita de una nave espacial (el resto del vuelo se llama “costa”).

objetivos de aprendizaje

• Explicar el propósito de una maniobra orbital

Maniobras orbitales

En los vuelos espaciales, una maniobra orbital es el uso de sistemas de propulsión para cambiar la órbita de una nave espacial. El resto del vuelo, especialmente en una órbita de transferencia, se denomina navegación por tierra.

Ecuación de cohete

La ecuación de cohete Tsiolkovsky o ecuación ideal de cohete es una ecuación útil para considerar vehículos que siguen el principio básico de un cohete: un dispositivo que puede aplicar aceleración a sí mismo (un empuje) expulsando parte de su masa a alta velocidad y moviéndose debido a la conservación del impulso. Específicamente, se trata de una ecuación matemática que relaciona el delta-v con la velocidad efectiva de escape y tanto la masa inicial como final de un cohete (u otro motor de reacción).

Para cualquier maniobra de este tipo (o viaje que implique una serie de tales maniobras):

\[\mathrm{Δv=v_e \ln (\dfrac{m_0}{m_1}),}\]

donde:

• m ₀ es la masa total inicial, incluido el propelente;
• m ₁ es la masa total final;
• v _e es la velocidad efectiva de escape (v _e =I _{sp •} g ₀ donde I _sp es el impulso específico expresado como un período de tiempo y g ₀ es la constante gravitacional); y
• Δv es delta-v el cambio máximo de velocidad del vehículo (sin que actúen fuerzas externas).

Véase para una ilustración que traza la relación entre la velocidad final y las relaciones de masa del cohete (según la ecuación del cohete).

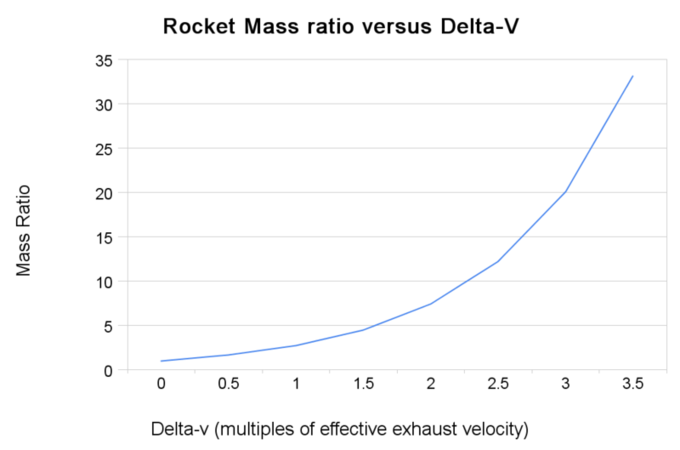
Ecuación del cohete: relaciones de masa del cohete frente a la velocidad final calculadas a partir

Presupuesto Delta-V:

El delta-v total por cada maniobra estimada para una misión se denomina presupuesto delta-v. Con una buena aproximación del presupuesto delta-v, los diseñadores pueden estimar los requisitos de combustible a carga útil de la nave espacial utilizando la ecuación del cohete.

Efecto Oberth y Asistencia Gravitacional

En astronáutica, el efecto Oberth ocurre cuando el uso de un motor cohete que viaja a alta velocidad genera mucha más energía útil que uno a baja velocidad. Este efecto es el resultado de que el propulsor tiene más energía utilizable (debido a su energía cinética sobre su energía potencial química). El vehículo es capaz de emplear esta energía cinética para generar más potencia mecánica.

El efecto Oberth se utiliza en una maniobra sobrevoladora o Oberth motorizada en la que la aplicación de un impulso (típicamente del uso de un motor de cohete) cerca de un cuerpo gravitacional (donde el potencial de gravedad es bajo y la velocidad es alta) permite un mayor cambio en la energía cinética y la velocidad final (es decir, mayor específica energía) que el mismo impulso aplicado más lejos del cuerpo para la misma órbita inicial.

En la mecánica orbital, una honda gravitacional (o maniobra de asistencia por gravedad) es el uso del movimiento relativo y la gravedad de un planeta u otro cuerpo celeste para alterar la trayectoria y la velocidad de una nave espacial, típicamente en un esfuerzo por ahorrar propulsor, tiempo y gastos. La asistencia por gravedad se puede utilizar para acelerar, desacelerar y/o redirigir la trayectoria de una nave espacial. Esta técnica fue utilizada por las sondas Voyager en sus fly-bys de Júpiter y Saturno (ver).

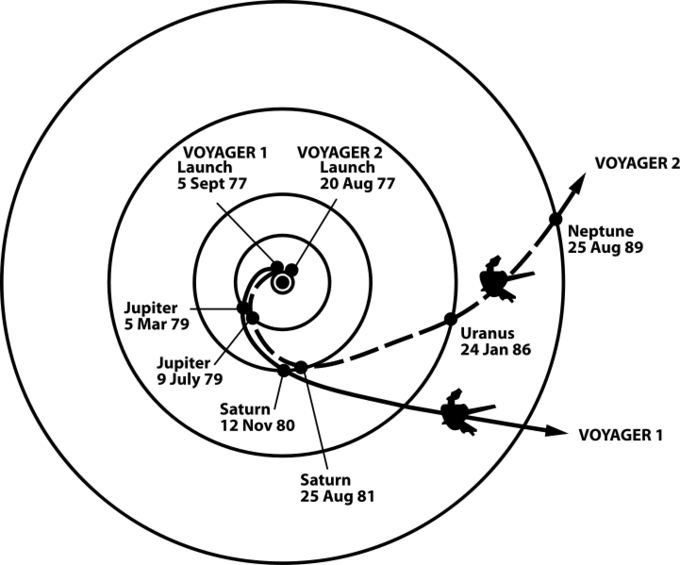
Voyager Path Using Gravity Assistes: Las trayectorias que permitieron a la nave espacial Voyager gemela de la NASA recorrer los cuatro planetas gigantes de gas y lograr velocidad para escapar de nuestro sistema solar

Órbitas de transferencia

La inserción de órbita es un término general utilizado para una maniobra cuando es más que una pequeña corrección. Se puede utilizar en una maniobra para cambiar una órbita de transferencia o una órbita de ascenso a una estable, pero también para cambiar una órbita estable en un descenso (es decir, inserción de órbita de descenso). También se utiliza el término inyección orbital, especialmente para cambiar una órbita estable en una órbita de transferencia, por ejemplo, inyección trans-lunar (TLI), inyección transMarte (TMI) e inyección transterrestre (TEI).

La órbita de transferencia de Hohmann es una órbita elíptica utilizada para transferir entre dos órbitas circulares de diferentes altitudes en un mismo plano. La maniobra orbital para realizar la transferencia de Hohmann utiliza dos impulsos de motor que mueven la nave espacial dentro y fuera de la órbita de transferencia, como se diagrama en. Las órbitas de transferencia de Hohmann son las más eficientes con combustible. Existen otros tipos de órbitas de transferencia no Hohmann que son menos eficientes con el combustible, pero estas pueden ser más eficientes con otros recursos (como el tiempo).

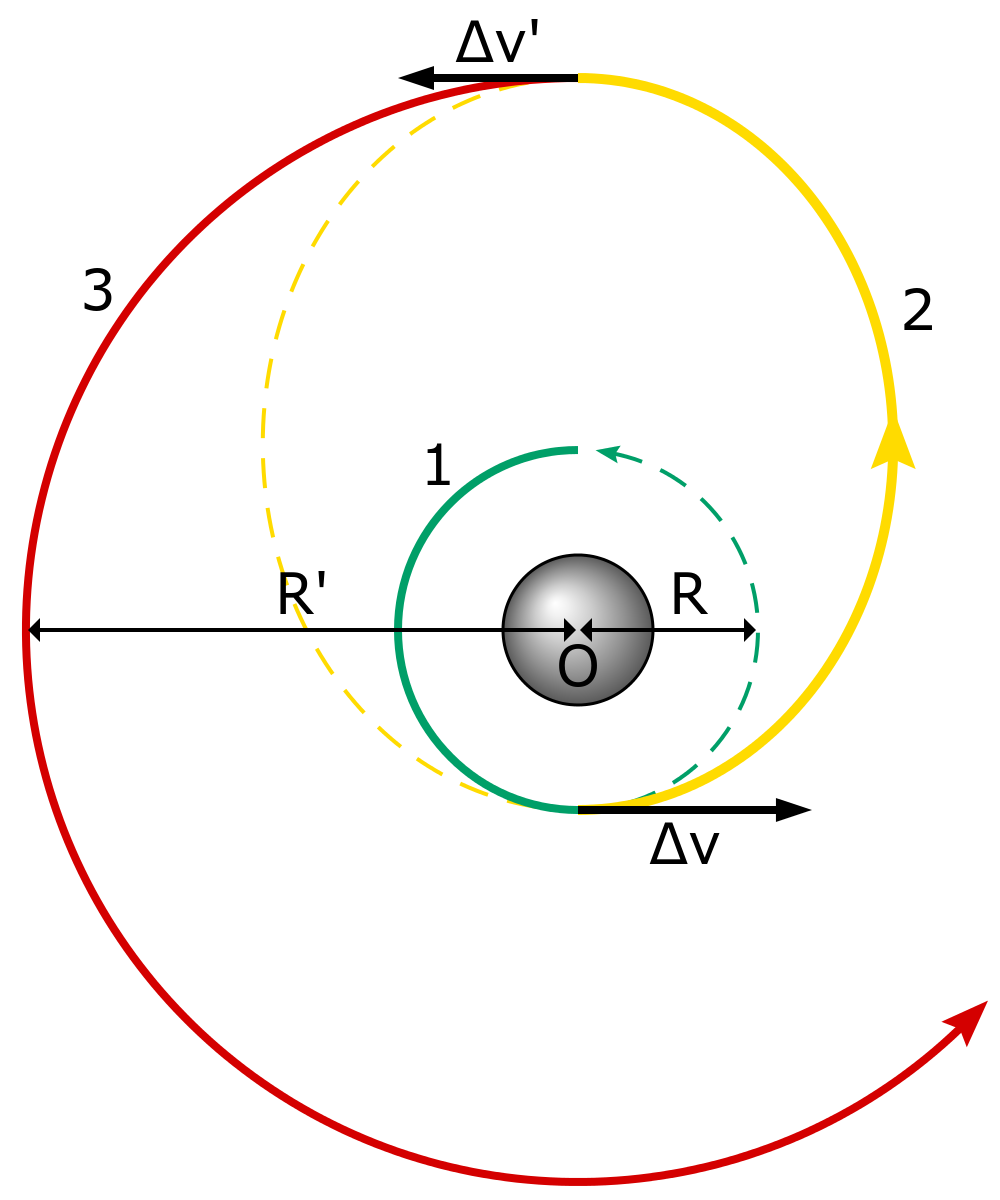
Órbita de Transferencia Hohmann: Un diagrama de la Órbita de Transferencia de Hohmann.

El cambio de inclinación orbital es una maniobra orbital dirigida a cambiar la inclinación de la órbita de un cuerpo en órbita (esta maniobra también se conoce como cambio de plano orbital ya que el plano de la órbita se inclina). La maniobra requiere un cambio en el vector de velocidad orbital (delta-v) en los nodos orbitales (es decir, el punto en el que se cruzan las órbitas inicial y deseada: la línea de nodos orbitales se define por la intersección de los dos planos orbitales).

Satélites

Los satélites naturales son objetos celestes que orbitan un cuerpo más grande; los satélites artificiales son objetos hechos por el hombre puestos en la órbita de la Tierra.

objetivos de aprendizaje

• Definir el concepto de satélite, en los términos más amplios posibles

Satélites

La palabra “satélite” tiene una definición algo ambigua. La definición más amplia posible de un satélite es un objeto que orbita uno más grande debido a la fuerza de la gravedad. Los satélites naturales, a menudo llamados lunas (ver), son cuerpos celestes que orbitan un cuerpo más grande llamado primario (a menudo planeta, aunque también hay asteroides binarios). Es técnicamente correcto referirse a un planeta como un “satélite” de su estrella madre, aunque esto no es común.

Lunas del Sistema Solar: Diecinueve satélites naturales son lo suficientemente grandes como para ser redondos, y uno, el Titán de Saturno, tiene una atmósfera sustancial.

Los satélites artificiales (ver) son objetos hechos por el hombre puestos en órbita alrededor de la Tierra u otro planeta en el Sistema Solar. Todos los satélites siguen las leyes de la mecánica orbital, que casi siempre pueden aproximarse con la física newtoniana.

Altitudes Orbitales: Altitudes orbitales de varios satélites significativos de la Tierra.

Los satélites naturales a menudo se clasifican en términos de su tamaño y composición, mientras que los satélites artificiales se clasifican en términos de sus parámetros orbitales.

Satélites Naturales

Los satélites naturales formalmente clasificados, o lunas, incluyen 176 satélites planetarios que orbitan seis de los ocho planetas, y ocho orbitando tres de los cinco planetas enanos incluidos en la lista IAU. A enero de 2012, se han descubierto más de 200 lunas de planeta menor. Hay 76 objetos en el cinturón de asteroides con satélites (cinco con dos satélites cada uno), cuatro troyanos de Júpiter, 39 objetos cercanos a la Tierra y 14 cruces Marte. También hay 84 satélites naturales conocidos de objetos transneptunianos. Es probable que los planetas alrededor de otras estrellas también tengan satélites naturales, aunque todavía no se ha observado ninguno.

De los planetas internos, Mercurio y Venus no tienen satélites naturales; la Tierra tiene un gran satélite natural, conocido como la Luna; y Marte tiene dos satélites naturales diminutos, Fobos y Deimos. Los grandes gigantes gaseosos tienen extensos sistemas de satélites naturales, entre ellos media docena comparables en tamaño a la Luna de la Tierra: las cuatro lunas galileas, el Titán de Saturno y el Tritón de Neptuno. Saturno tiene seis satélites naturales de tamaño mediano adicionales lo suficientemente masivos como para haber logrado el equilibrio hidrostático, y Urano tiene cinco. Se ha sugerido que algunos satélites pueden potencialmente albergar vida, aunque actualmente no hay evidencia directa.

El sistema Tierra-Luna es único en el sentido de que la relación entre la masa de la Luna y la masa de la Tierra es mucho mayor que la de cualquier otra relación satélite natural a planeta en el Sistema Solar. Adicionalmente la órbita de la Luna con respecto al Sol es siempre cóncava.

Los siete satélites naturales más grandes del Sistema Solar (aquellos de más de 2.500 km de diámetro) son las lunas galileas de Júpiter (Ganímedes, Calisto, Io y Europa), la luna de Saturno Titán, la luna de la Tierra y el satélite natural capturado de Neptuno, Tritón.

Satélites Artificiales

El primer satélite, Sputnik 1, se puso en órbita alrededor de la Tierra y por lo tanto se encontraba en órbita geocéntrica. Con mucho, este es el tipo de órbita más común con cerca de 2.500 satélites artificiales orbitando la Tierra. Las órbitas geocéntricas pueden clasificarse aún más por su altitud, inclinación y excentricidad.

Las clasificaciones de altitud comúnmente utilizadas son órbita terrestre baja (LEO), órbita terrestre media (MEO) y órbita terrestre alta (HEO). La órbita terrestre baja es cualquier órbita inferior a 2000 km, y la órbita de la Tierra Media es cualquier órbita más alta que esa pero aún por debajo de la altitud para órbita geosincrónica a 35.786 km. La órbita terrestre alta es cualquier órbita mayor que la altitud de la órbita geosincrónica.

Clasificaciones de altitud

• Órbita terrestre baja (LEO): Órbitas geocéntricas que van en altitud de 0 a 2000 km (0 a 1240 millas)
• Órbita terrestre media (MEO): Órbitas geocéntricas que van en altitud desde 2,000 km (1,200 mi) hasta justo debajo de la órbita geosincrónica a 35,786 km (22,236 mi). También conocida como órbita circular intermedia.
• Órbita terrestre alta (HEO): Órbitas geocéntricas por encima de la altitud de la órbita geosincrónica 35,786 km (22,236 mi).

Clasificaciones de Inclinación

• Órbita inclinada: Órbita cuya inclinación en referencia al plano ecuatorial no es de cero grados.
• Órbita polar: Una órbita que pasa por encima o casi por encima de ambos polos del planeta en cada revolución. Por lo tanto, tiene una inclinación de (o muy cercana a) 90 grados.
• Órbita síncrona solar polar: Una órbita casi polar que pasa por el ecuador a la misma hora local en cada pasada. Útil para satélites de toma de imágenes porque las sombras serán casi las mismas en cada pasada.

Clasificaciones de excentricidad

• Órbita circular: Una órbita que tiene una excentricidad de 0 y cuya trayectoria traza un círculo.
• Órbita de transferencia Hohmann: Una maniobra orbital que mueve una nave espacial de una órbita circular a otra utilizando dos impulsos de motor.
• Órbita elíptica: Una órbita con una excentricidad mayor que 0 e inferior a 1 cuya órbita traza la trayectoria de una elipse.
• Órbita de transferencia geosincrónica: Una órbita elíptica donde el perigeo se encuentra a la altitud de una órbita terrestre baja (LEO) y el apogeo a la altitud de una órbita geosincrónica.
• Órbita de transferencia geoestacionaria: Una órbita elíptica donde el perigeo se encuentra a la altitud de una órbita terrestre baja (LEO) y el apogeo a la altitud de una órbita geoestacionaria.

Puntos Clave

• Una elipse es una curva plana cerrada que se asemeja a un círculo estirado (El Sol está en un foco mientras que el otro foco no tiene significado físico. Un círculo es un caso especial de elipse donde ambos puntos focales coinciden.
• Cuán estirada está una elipse a partir de un círculo perfecto se conoce como su excentricidad: un parámetro que puede tomar cualquier valor mayor o igual a 0 (un círculo) e inferior a 1 (como la excentricidad tiende a 1, la elipse tiende a una parábola).
• Simbólicamente, una elipse se puede representar en coordenadas polares como:\(\mathrm{r=\frac{p}{1+ϵ \cos ⁡θ}}\), donde\(\mathrm{(r,θ)}\) están las coordenadas polares (desde el foco) para la elipse,\(\mathrm{p}\) es el recto semilatoso, y\(\mathrm{ϵ}\) es la excentricidad de la elipse.
• Perihelio es la distancia mínima del Sol que un planeta logra en su órbita y es dado por\(\mathrm{r_{max}=\frac{p}{1−ϵ}.}\) Afelio es la distancia más grande del Sol que alcanza un planeta en su órbita y está dada por\(\mathrm{r_{max}=\dfrac{p}{1−ϵ}.}\)
• En poco tiempo el planeta barre un pequeño triángulo que tiene línea base y altura. El área de este triángulo viene dada por\(\mathrm{dA=\frac{1}{2}⋅r⋅rdθ}\) y así la velocidad de área constante es:\(\mathrm{\frac{dA}{dt}=\dfrac{1}{2}r^2\dfrac{dθ}{dt}}\)
• El periodo\(\mathrm{P}\) satisface:\(\mathrm{πab=P⋅\frac{1}{2}r^2 \dot{θ}}\). Se puede ver que el producto de\(\mathrm{r^2}\) y debe ser constante, de manera que cuando el planeta está más lejos del Sol viaja a un ritmo más lento y viceversa.
• Un planeta viaja más rápido en el perihelio y más lento en el afelio.
• La tercera ley de Kepler se puede representar simbólicamente como\(\mathrm{P^2∝a^3,}\) donde P es el período orbital del planeta y a es el semieje mayor de la órbita (ver.
• La constante de proporcionalidad es\(\mathrm{\dfrac{P_{planet}^2}{a_{planet}^3}=\frac{P_{earth}^2}{a_{earth}^3}=1\frac{yr^2}{AU^3}}\) para un año sideral (año), y unidad astronómica (AU).
• La tercera ley de Kepler puede derivarse de las leyes del movimiento de Newton y de la ley universal de la gravitación. Establecer la fuerza de gravedad igual a la fuerza centrípeta. Después de sustituir una expresión por la velocidad del planeta, se puede obtener:\(\mathrm{G\frac{M}{r}=\frac{4πr^2}{P^2}}\) que también se puede escribir\(\mathrm{P^2=\frac{4π^2a^3}{GM}.}\)
• Usando la expresión anterior podemos obtener la masa del cuerpo padre a partir de las órbitas de sus satélites:\(\mathrm{M=\frac{4π^2r^3}{GP^2}}\)
• La ecuación ideal del cohete relacionó el cambio máximo en la velocidad alcanzable por un cohete (delta-v o Δv) en función de la velocidad de escape (v _e) y la relación entre la masa del cohete con y sin el propulsor (m ₀ /m ₁). La ecuación viene dada por\(\mathrm{Δv=v_e \ln (\dfrac{m_0}{m_1})}\).
• El efecto Oberth: donde el uso de un motor cohete que viaja a alta velocidad genera más energía útil que uno a baja velocidad. Por lo tanto, es más eficiente aplicar empuje cuando la nave espacial está más cerca del planeta (periastrón).
• Una maniobra de asistencia por gravedad es el uso del movimiento relativo y la gravedad de un planeta (u otro cuerpo celeste) para alterar la velocidad de una nave espacial, típicamente con el fin de ahorrar propulsor, tiempo y gastos. Esta técnica fue empleada por las sondas Voyager (ver.
• La órbita de transferencia de Hohmann es una órbita elíptica utilizada para transferir entre dos órbitas circulares de diferentes altitudes, en un mismo plano. La maniobra orbital para realizar la transferencia de Hohmann utiliza dos impulsos motores que mueven la nave espacial dentro y fuera de la órbita de transferencia. Ver.
• La definición más amplia posible de un satélite es un objeto que orbita uno más grande debido a la fuerza de la gravedad.
• Todos los satélites siguen las leyes de la mecánica orbital, que casi siempre pueden aproximarse con la física newtoniana.
• Los satélites naturales a menudo se clasifican en términos de su tamaño y composición, mientras que los satélites artificiales se clasifican en términos de sus parámetros orbitales.
• Los satélites artificiales en órbita terrestre tienen órbitas categorizadas por sus altitudes, inclinaciones y excentricidades.

Términos Clave

• excentricidad: El coeficiente de variación entre\(\mathrm{r_{min}}\) y\(\mathrm{r_{max}}\):\(\mathrm{ϵ=\dfrac{r_{max}−r_{min}}{r_{max}+r_{min}}}\) Cuanto más separados estén los focos, más fuerte será la excentricidad.
• perihelio: El punto en la órbita elíptica de un planeta o cometa etc. donde está más cercano al Sol. El punto más alejado del Sol se llama afelio.
• recto semilatoso: El recto latus es una cuerda perpendicular al eje mayor y que pasa por el foco. El recto semilatoso es la mitad del rectro del latus. Ver distancia p. in.
• velocidad angular: Una cantidad vectorial que describe un objeto en movimiento circular; su magnitud es igual a la velocidad de la partícula y la dirección es perpendicular al plano de su movimiento circular.
• movimiento medio: Un ángulo de\(\mathrm{2π}\) (radianes) dividido por el período orbital (de un cuerpo celeste en una órbita elíptica).
• unidad astronómica: La distancia media de la Tierra al Sol (el semieje mayor de la órbita terrestre), aproximadamente 149,600,000 kilómetros (símbolo AU), utilizada para medir distancias en el sistema solar.
• Año sideral: El periodo orbital de la Tierra; una medida del tiempo que tarda el Sol en regresar a la misma posición con respecto a las estrellas de la esfera celeste. Un año sideral es aproximadamente 20.4 minutos más largo que el año tropical debido a la precesión de los equinoccios.
• Órbita de transferencia de Hohmann: La órbita de transferencia de Hohmann es una órbita elíptica utilizada para transferir entre dos órbitas circulares de diferentes altitudes, en un mismo plano. La maniobra orbital para realizar la transferencia de Hohmann utiliza dos impulsos de motor, uno para mover una nave espacial a la órbita de transferencia y otro para alejarse de ella.
• delta-v: El cambio máximo en la velocidad escalar de un cohete si el cohete se operaba en un vacío alejado de fuerzas externas (es decir, si no actúan otras fuerzas externas).
• satélite natural: Un satélite natural, luna o planeta secundario es un cuerpo celeste que orbita un planeta o cuerpo más pequeño, que se llama su primario.
• satélite artificial: En el contexto de los vuelos espaciales, un satélite es un objeto que ha sido puesto en órbita por el esfuerzo humano.

LICENCIAS Y ATRIBUCIONES

CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

• Curación y Revisión. Proporcionado por: Boundless.com. Licencia: CC BY-SA: Atribución-CompartirIgual