Saltar al contenido principal
LibreTexts Español

9.2: Aceleración angular

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128495
    • Boundless
    • Boundless

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\dsum}{\displaystyle\sum\limits} \)

    \( \newcommand{\dint}{\displaystyle\int\limits} \)

    \( \newcommand{\dlim}{\displaystyle\lim\limits} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \(\newcommand{\longvect}{\overrightarrow}\)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Relacionar el ángulo de rotación, la velocidad angular y la aceleración angular con sus equivalentes en cinemática lineal

    Simplemente usando nuestra intuición, podemos comenzar a ver la interrelación de cantidades rotacionales como θ (ángulo de rotación), ω (velocidad angular) y α (aceleración angular). Por ejemplo, si una rueda de motocicleta tiene una aceleración angular grande durante bastante tiempo, termina girando rápidamente y girando a través de muchas revoluciones. El movimiento de rotación de la rueda es análogo al hecho de que la gran aceleración traslacional de la motocicleta produce una gran velocidad final, y la distancia recorrida también será grande.

    Ecuaciones Cinemáticas

    La cinemática es la descripción del movimiento. Ya hemos estudiado ecuaciones cinemáticas que rigen el movimiento lineal bajo aceleración constante:

    \[\begin{align} \mathrm{v} & \mathrm{=v_0+at} \\ \mathrm{x} & \mathrm{=v_0t+\frac{1}{2}at^2} \\ \mathrm{v^2} & \mathrm{=v_0^2+2ax} \end{align}\]

    De manera similar, la cinemática del movimiento rotacional describe las relaciones entre el ángulo de rotación, la velocidad angular, la aceleración angular y el tiempo. Empecemos por encontrar una ecuación que relacione ω, α y t. Para determinar esta ecuación, usamos la ecuación correspondiente para el movimiento lineal:

    \[\mathrm{v=v_0+at.}\]

    Al igual que en la cinemática lineal donde asumimos que a es constante, aquí asumimos que la aceleración angular α es una constante, y podemos usar la relación:\(\mathrm{a=rα}\) Donde r — radio de curva. Del mismo modo, tenemos las siguientes relaciones entre valores lineales y angulares:

    \[\begin{align} \mathrm{v} & \mathrm{=rω} \\ \mathrm{x} & \mathrm{=rθ} \end{align}\]

    Mediante el uso de las relaciones\(\mathrm{a=rα, v=rω,}\) y\(\mathrm{x=rθ}\), derivamos todas las demás ecuaciones cinemáticas para el movimiento rotacional bajo aceleración constante:

    \[\begin{align} \mathrm{ω} & \mathrm{=ω_0+αt} \\ \mathrm{θ} & \mathrm{=ω_0t+\frac{1}{2}αt^2} \\ \mathrm{ω^2} & \mathrm{= ω_0^2+2αθ} \end{align}\]

    Las ecuaciones dadas anteriormente pueden ser utilizadas para resolver cualquier problema de cinemática rotacional o traslacional en el que a y α sean constantes. muestra la relación entre algunas de las cantidades discutidas en este átomo.

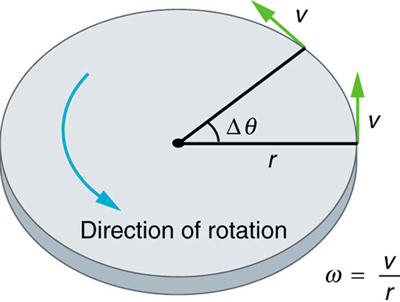
    imagen

    Lineal y Angular: Esta figura muestra un movimiento circular uniforme y algunas de sus cantidades definidas.

    Puntos Clave

    • Las ecuaciones cinemáticas para movimiento rotacional y/o lineal dadas aquí pueden ser utilizadas para resolver cualquier problema de cinemática rotacional o traslacional en el que a y α sean constantes.
    • Mediante el uso de las relaciones entre velocidad y velocidad angular, distancia y ángulo de rotación, y aceleración y aceleración angular, las ecuaciones cinemáticas rotacionales se pueden derivar de sus contrapartes de movimiento lineal.
    • Para derivar ecuaciones rotacionales de las contrapartes lineales, se utilizaron las relaciones\(\mathrm{a=rα, v=rω,}\) y\(\mathrm{x=rθ}\).

    Términos Clave

    • cinemática: La rama de la mecánica que se ocupa de los objetos en movimiento, pero no de las fuerzas involucradas.
    • angular: Relativo a un ángulo o ángulos; tener un ángulo o ángulos; formar un ángulo o esquina; con esquinas agudas; puntiagudas; puntiagudas; como en, una figura angular.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    This page titled 9.2: Aceleración angular is shared under a not declared license and was authored, remixed, and/or curated by Boundless.