Saltar al contenido principal
LibreTexts Español

9.9: Cantidades lineales y rotacionales

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128511

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    objetivos de aprendizaje

    • Derivar movimiento circular uniforme a partir de ecuaciones lineales

    Definición de Movimiento Circular

    La descripción del movimiento circular se describe mejor en términos de cantidad angular que su contraparte lineal. Las razones son fáciles de entender. Por ejemplo, considere el caso del movimiento circular uniforme. Aquí, la velocidad de las partículas está cambiando, aunque el movimiento es “uniforme”. Los dos conceptos no van juntos. La connotación general del término “uniforme” indica “constante”, pero la velocidad en realidad está cambiando todo el tiempo.

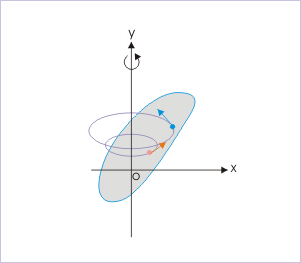
    imagen

    Un Cuerpo Giratorio: Cada partícula que constituye el cuerpo ejecuta un movimiento circular uniforme alrededor del eje fijo. Para la descripción del movimiento, las cantidades angulares son la mejor opción.

    Cuando describimos el movimiento circular uniforme en términos de velocidad angular, no hay contradicción. La velocidad (es decir, la velocidad angular) es realmente constante. Esta es la primera ventaja de describir el movimiento circular uniforme en términos de velocidad angular.

    La segunda ventaja es que la velocidad angular transmite el sentido físico de la rotación de la partícula frente a la velocidad lineal, lo que indica movimiento de traslación. Alternativamente, la descripción angular enfatiza la distinción entre dos tipos de movimiento (traslacional y rotacional).

    Relación entre velocidad lineal y angular

    Para simplificar, consideremos un movimiento circular uniforme. Para la longitud del arco subtendiendo ángulo” en el origen y “r” es el radio del círculo que contiene la posición de la partícula, tenemos\(\mathrm{s=rθ}\).

    Diferenciando con respecto al tiempo, tenemos

    \[\mathrm{\dfrac{ds}{dt}=\dfrac{dr}{dt}θ+r\dfrac{dθ}{dt}.}\]

    Porque\(\mathrm{\frac{dr}{dt}=0}\) para un movimiento circular uniforme, obtenemos\(\mathrm{v=ωr}\). Del mismo modo, también obtenemos\(\mathrm{a=αr}\) donde\(\mathrm{a}\) significa aceleración lineal, mientras que\(\mathrm{α}\) se refiere a la aceleración angular (En un caso más general, la relación entre las cantidades angulares y lineales se da como\(\mathrm{ v=ω \times r, a=α \times r+ω \times v}\)

    Ecuaciones cinemáticas rotacionales

    Con la relación de la velocidad/aceleración lineal y angular, podemos derivar las siguientes cuatro ecuaciones cinemáticas rotacionales para aa y αα constantes:

    \[\begin{align} \mathrm{ω} & \mathrm{=ω_0+αt:v=v_0+at} \\ \mathrm{θ} & \mathrm{=ω_0t+(\dfrac{1}{2})αt^2:x=v_0t+(\dfrac{1}{2})at^2} \\ \mathrm{ω^2} & \mathrm{=ω_0^2+2 \alpha \theta :v^2=v_0^2+2ax}\end{align}\]

    Masa, Momentum, Energía y Segunda Ley de Newton

    A medida que usamos la masa, el momento lineal, la energía cinética traslacional y la segunda ley de Newton para describir el movimiento lineal, podemos describir un movimiento rotacional general usando las cantidades escalares/vector/tensor correspondientes:

    • Masia/inercia rotacional:
    • Momento linenal/angular:
    • Fuerza/Torque:
    • Energía cinética:

    Por ejemplo, así como usamos la ecuación de movimiento F=MAF=Ma para describir un movimiento lineal, podemos usar su contraparte\(\mathrm{τ=\frac{dL}{dt}=r \times F}\) para describir un movimiento angular. Las descripciones son equivalentes, y la elección se puede hacer puramente por conveniencia de uso.

    Puntos Clave

    • Al utilizar la masa, el momento lineal, la energía cinética traslacional y la segunda ley de Newton para describir el movimiento lineal, podemos describir un movimiento rotacional general usando las cantidades escalares/vector/tensor correspondientes.
    • La velocidad angular y lineal tienen la siguiente relación:\(\mathrm{v=ω \times r}\).
    • Al usar la ecuación de movimiento\(\mathrm{F=ma}\) para describir un movimiento lineal, podemos usar su contraparte\(\mathrm{τ=\frac{dL}{dt}=r \times F}\), para describir el movimiento angular. Las descripciones son equivalentes, y la elección se puede hacer puramente por conveniencia de uso.

    Elementos clave

    • Movimiento circular uniforme: Movimiento alrededor de una trayectoria circular con velocidad constante.
    • par: Un efecto de rotación o torsión de una fuerza; (unidad SI newton-metro o Nm; unidad imperial pie-libra o ft-lb)
    • inercia rotacional: La tendencia de un objeto giratorio a permanecer girando a menos que se le aplique un par.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    9.9: Cantidades lineales y rotacionales is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.