6.1: Estática

Al usar las leyes de Newton para modelar un objeto, se pueden identificar dos categorías amplias de situaciones: estáticas y dinámicas. En situaciones estáticas, la aceleración del objeto es cero. Por la Segunda Ley de Newton, esto quiere decir que la suma vectorial de las fuerzas (y los pares, como veremos en un capítulo posterior) ejercidas sobre un objeto debe ser cero. En situaciones dinámicas, la aceleración del objeto es distinta de cero.

Para problemas estáticos, dado que el vector de aceleración es cero, podemos elegir un sistema de coordenadas de una manera que resulte en que se alineen tantas fuerzas como sea posible con los ejes (de modo que minimizamos el número de fuerzas que necesitamos para descomponer en componentes).

Ejemplo\(\PageIndex{1}\)

Y ou empujar horizontalmente con una fuerza\(\vec F\) on a box of mass \(m\) that is resting against a vertical wall, as shown in Figure \(\PageIndex{1}\). The coefficient of static friction between the wall and the box is \(\mu_s\). What is the minimum magnitude of the force that you must exert for the box to remain stationary?

Solución:

Figura\(\PageIndex{1}\): Una fuerza horizontal ejercida sobre la caja que se encuentra apoyada contra una pared.

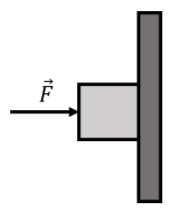
Dado que la aceleración de la caja es cero, la suma vectorial de las fuerzas ejercidas sobre la caja es cero. Comenzamos por identificar las fuerzas ejercidas sobre la caja; estas son:

1. \(\vec F\), la fuerza horizontal que ejerces sobre la caja.
2. \(\vec F_g\), el peso de la caja, con magnitud\(mg\).
3. \(\vec N\), una fuerza normal ejercida por la pared sobre la caja. La fuerza está en la dirección horizontal, en la dirección opuesta a\(\vec F\).
4. \(\vec f_s\), una fuerza vertical de fricción estática entre la pared y la caja. La fuerza apunta hacia arriba ya que el “movimiento obstaculizante” del bloque es hacia abajo. La fuerza tendrá como máximo una magnitud de\(f_s\leq\mu_s N\), ya que la fuerza de fricción estática depende de las otras fuerzas ejercidas sobre el objeto.

Las fuerzas se muestran en el diagrama de cuerpo libre de la Figura 6.1.2, junto con nuestra elección del sistema de coordenadas que se eligió de manera que todas las fuerzas estén en la\(y\) dirección\(x\) o en la dirección.

Figura\(\PageIndex{2}\): Diagrama de cuerpo libre de las fuerzas ejercidas sobre la caja.

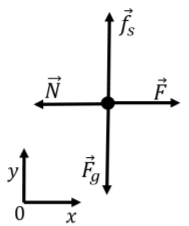
El\(x\) componente de la Segunda Ley de Newton es:\[\begin{aligned} \sum F_x = F - N &=0\\ \therefore N = F\end{aligned}\] que nos dice que la fuerza normal ejercida por el muro tiene la misma magnitud que la fuerza aplicada,\(\vec F\). El\(y\) componente de la Segunda Ley de Newton es:\[\begin{aligned} \sum F_y = f_s - F_g &=0\\ \therefore f_s -mg &=0\\ \therefore f_s = mg\\\end{aligned}\] que nos dice que la fuerza de fricción debe tener la misma magnitud que el peso. Esto tiene sentido, ya que son las únicas fuerzas con componentes en la\(y\) dirección, y así, deben cancelarse entre sí.

La fuerza de fricción será menor o igual a\(\mu_sN\), y por lo tanto menor o igual a\(\mu_s F\), ya que\(\vec F\) y\(\vec N\) tendrá la misma magnitud (a partir del\(x\) componente de la Segunda Ley de Newton). Además, ya que\(f_s=mg\), podemos escribir:\[\begin{aligned} f_s &\leq \mu_s F\\ \therefore mg &\leq \mu_s F\\ \therefore \frac{mg}{\mu_s} &\leq F\end{aligned}\] lo que nos da la condición que\(F\geq mg/\mu_s\), y así la mínima magnitud de\(F\) para evitar que la caja se deslice hacia abajo.

A pesar de que usamos el signo menor que o igual en las ecuaciones anteriores, podríamos haber utilizado un signo igual si estuviéramos seguros de que la fuerza de fricción tiene su magnitud máxima,\(f_s=\mu_sN\). La magnitud máxima de la fuerza de fricción es proporcional a la fuerza que ejercemos (ya que\(N=F\)); si queremos ejercer la menor cantidad de fuerza\(F\), entonces necesitamos que la fuerza de fricción sea igual a su magnitud máxima que necesita ser igual al peso de la caja .

Discusión:

Este modelo para la fuerza mínima requerida tiene sentido porque:

• La dimensión de\(mg/\mu_s\) es la fuerza.
• Si se aumenta la masa de la caja, entonces uno necesita empujar más fuerte contra la caja para que siga así.
• Si el coeficiente de fricción estática\(\mu_s\),, se incrementa, no se necesita empujar tan fuerte.