6.2: Movimiento lineal
- Page ID
- 129135
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Podemos describir el movimiento de un objeto cuyo vector de velocidad no cambia continuamente de dirección como movimiento “lineal”. Por ejemplo, un objeto que se mueve a lo largo de una línea recta en una dirección particular, luego cambia bruscamente de dirección y continúa moviéndose en línea recta puede modelarse como experimentando movimiento lineal sobre dos segmentos diferentes (que modelaríamos individualmente). Un objeto que se mueve alrededor de un círculo, con su vector de velocidad continuamente cambiando de dirección, no se consideraría que estuviera experimentando un movimiento lineal. Por ejemplo, las trayectorias de objetos que experimentan movimiento lineal y no lineal se ilustran en la Figura\(\PageIndex{1}\).
Cuando un objeto experimenta un movimiento lineal, siempre modelamos el movimiento del objeto sobre segmentos rectos por separado. Sobre uno de esos segmentos, el vector de aceleración será colineal con el vector de desplazamiento del objeto (paralelo o antiparalelo - tenga en cuenta que la aceleración puede cambiar de dirección como lo haría a partir de una fuerza de resorte, pero siempre será colineal con el desplazamiento).
Ejemplo\(\PageIndex{1}\)
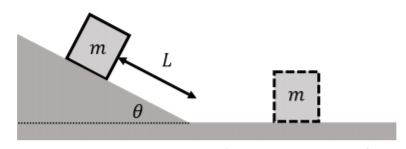
[ex:applyingnewtonslaws:block] Un bloque de masa\(m\) se coloca en reposo sobre una pendiente que forma un ángulo\(\theta\) con respecto a la horizontal, como se muestra en la Figura\(\PageIndex{2}\). El bloque se empuja ligeramente para que se supere la fuerza de fricción estática y el bloque comience a acelerar hacia abajo por la pendiente. En la parte inferior de la inclinación, el bloque se desliza sobre una superficie horizontal.
El coeficiente de fricción cinética entre el bloque y la inclinación es\(\mu_{k1}\), y el coeficiente de fricción cinética entre el bloque y la superficie horizontal es\(\mu_{k2}\). Si se asume que el bloque comenzó en reposo a una distancia\(L\) del fondo de la inclinación, ¿a qué distancia a lo largo de la superficie horizontal se deslizará el bloque antes de detenerse?
Solución:
Podemos identificar que se trata de un movimiento lineal que podemos dividir en dos segmentos: (1) el movimiento por la pendiente, y (2), el movimiento a lo largo de la superficie horizontal. Así identificaremos las fuerzas, dibujaremos el diagrama de cuerpo libre para el bloque y usaremos la Segunda Ley de Newton dos veces, una por cada segmento.
A menudo es útil describir el movimiento en palabras para ayudarnos a identificar los pasos requeridos en la construcción de un modelo para el bloque. En este caso podríamos decir que:
- El bloque se desliza por la pendiente y acelera en la dirección del movimiento. Al identificar las fuerzas y aplicar la Segunda Ley de Newton, podemos determinar su aceleración que será paralela a la pendiente.
- El bloque alcanzará cierta velocidad en la parte inferior de la pendiente, que podemos determinar a partir de la cinemática al saber que el bloque viajó una distancia\(L\), con una aceleración conocida y que arrancó en reposo.
- El bloque se desacelerará a lo largo de la superficie horizontal. Nuevamente, al identificar las fuerzas y usar la Segunda Ley de Newton, podremos determinar la aceleración del bloqueo.
- El bloque se detendrá después de haber recorrido una distancia desconocida, la cual podremos encontrar utilizando la cinemática y conociendo la aceleración del bloque así como su velocidad inicial en la parte inferior de la pendiente.
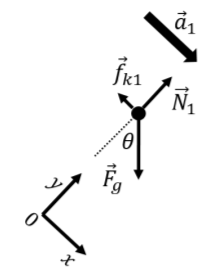
Nuestro primer paso es así identificar las fuerzas en el bloque mientras está en la pendiente. Estos son:
- \(\vec F_{g}\), su peso.
- \(\vec N_1\), una fuerza normal ejercida por la inclinación.
- \(\vec f_{k1}\), una fuerza de fricción cinética ejercida por la inclinación. La fuerza es opuesta a la dirección del movimiento, y tiene una magnitud dada por\(f_{k1}=\mu_{k1}N_1\).
Estos se muestran en el diagrama de cuerpo libre en la Figura\(\PageIndex{3}\). Como es habitual, dibujamos la aceleración,\(\vec a_1\), en el diagrama de cuerpo libre, y elegimos la dirección del\(x\) eje para que fuera paralela a la aceleración.
Escribiendo el\(x\) componente de la Segunda Ley de Newton, y utilizando el hecho de que la aceleración está en la\(x\) dirección (\(\vec a=a_1\hat x\)):\[\begin{aligned} \sum F_x = F_g\sin\theta - f_{k1} &= ma_1\\ \therefore mg\sin\theta - \mu_{k1} N_1 &= ma_1\end{aligned}\] donde expresamos la magnitud de la fuerza cinética de fricción en términos de la fuerza normal ejercida por el plano, y el peso en términos de la masa y el campo gravitacional,\(g\). Se puede escribir el\(y\) componente de la Segunda Ley de Newton: el\[\begin{aligned} \sum F_y = N_1-F_g\cos\theta &= 0\\ \therefore N_1 = mg\cos\theta\end{aligned}\] cual usamos para expresar la fuerza normal en términos del peso. Podemos usar esta expresión para la fuerza normal sustituyéndola en la ecuación que obtuvimos del\(x\) componente para encontrar la aceleración a lo largo de la pendiente:\[\begin{aligned} mg\sin\theta - \mu_{k1} N_1 &= ma_1\\ mg\sin\theta - \mu_{k1} mg\cos\theta&= ma_1\\ \therefore a_1 &= g(\sin\theta-\mu_{k1}\cos\theta)\end{aligned}\] Ahora que conocemos la aceleración por la pendiente, podemos encontrar fácilmente la velocidad en la parte inferior de la inclinación utilizando cinemática. Elegimos el origen del\(x\) eje para que sea cero donde comenzó el bloque (\(x_0=0\)), de manera que el bloque esté en posición\(x=L\) en la parte inferior de la pendiente. Usando la cinemática, podemos encontrar la velocidad,\(v\), dado que la velocidad inicial,\(v_0=0\): Ahora\[\begin{aligned} v^2-v_0^2&=2a_1(x-x_0)\\ v^2&=2a_1L\\ \therefore v &= \sqrt{2a_1L}\\ &=\sqrt{2Lg(\sin\theta-\mu_{k1}\cos\theta)}\end{aligned}\] podemos proceder a construir un modelo para el segundo segmento. Primero identificamos las fuerzas sobre el bloque cuando está en la superficie horizontal; estas son:
- \(\vec F_{g1}\), su peso.
- \(\vec N_2\), una fuerza normal ejercida por la superficie horizontal. Esto es en general diferente a la fuerza normal ejercida cuando el bloque estaba en el plano inclinado.
- \(\vec f_{k2}\), una fuerza de fricción cinética ejercida por la superficie horizontal. La fuerza es opuesta a la dirección del movimiento, y tiene una magnitud dada por\(f_{k2}=\mu_{k2}N_2\).
Las fuerzas son ilustradas por el diagrama de cuerpo libre en la Figura\(\PageIndex{4}\), donde mostramos el vector de aceleración\(\vec a_2\), que determinamos que está a la izquierda ya que el bloque está desacelerando. También elegimos un sistema de\(xy\) coordenadas tal que el\(x\) eje sea antiparalelo a la aceleración, de manera que el movimiento esté en la\(x\) dirección positiva (y la aceleración en la\(x\) dirección negativa).
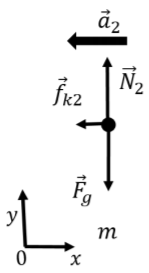
Escribiendo el\(x\) componente de la Segunda Ley de Newton:\[\begin{aligned} \sum F_x = -f_{k2} &= -ma_2\\ \therefore \mu_{k2}N_2 &= ma_2\end{aligned}\] donde expresamos la fuerza de fricción cinética usando la fuerza normal. Tenemos que tener cuidado aquí con el signo de la aceleración; la ecuación que escribimos implica que\(a_2\) es un número positivo, ya que\(\mu_{k2}\) es positivo y también\(N_2\) es positivo (es la magnitud de la fuerza normal). \(a_2\)es la magnitud de la aceleración, e incluimos el hecho de que la aceleración apunta en la\(x\) dirección negativa cuando ponemos un signo negativo en la primera línea. El\(x\) componente de la aceleración es\(-a_2\), y el vector viene dado por\(\vec a_2=-a_2\hat x\).
El\(y\) componente de la Segunda Ley de Newton nos permitirá encontrar la fuerza normal: la\[\begin{aligned} \sum F_y = N_2 -F_g &=0\\ \therefore N_2 = mg\end{aligned}\] cual podemos sustituir de nuevo en la\(x\) ecuación para encontrar la magnitud de la aceleración a lo largo de la superficie horizontal:\[\begin{aligned} ma_2 &=\mu_{k2}N_2 \\ \therefore a_2&=\mu_{k2}g\end{aligned}\] Ahora que hemos encontrado la aceleración a lo largo la superficie horizontal, podemos utilizar la cinemática para encontrar la distancia que recorrió el bloque antes de detenerse. Elegimos el origen del\(x\) eje para que sea la parte inferior de la inclinación (\(x_0=0\)), la aceleración es negativa\(a_x = -a_2 = -mu_{k2}g\), la velocidad final es cero\(v=0\), y la velocidad inicial,\(v_0\) viene dada por nuestro modelo para la primera segmento. Usando una de las ecuaciones cinemáticas:\[\begin{aligned} v^2-v_0^2&=2(-a_2)(x-x_0)\\ v_0^2&=2a_2x\\ \therefore x &=\frac{1}{2a_2}v_0^2\\ &=\frac{1}{2\mu_{k2}g}2Lg(\sin\theta-\mu_{k1}\cos\theta)\\ \therefore x&=\frac{(\sin\theta-\mu_{k1}\cos\theta)}{\mu_{k2}}L\end{aligned}\]
Discusión:
El modelo para la distancia\(x\) que tarda el bloque en detenerse tiene sentido porque:
- Todos los términos en la fracción son adimensionales, por lo que el valor de\(x\) tendrá la misma dimensión que\(L\).
- Si hacemos\(L\) más grande, entonces\(x\) será más grande (si soltamos el bloque de arriba hacia arriba en la pendiente, tendrá más tiempo para acelerar y se deslizará más antes de detenerse).
- Si hacemos\(\mu_{k1}\) más grande, entonces\(x\) será más pequeño: si aumentamos la fricción en la inclinación, el bloque tendrá una aceleración menor y menor velocidad en la parte inferior.
- Si aumentamos la fricción con el plano horizontal (aumento\(\mu_{k2}\)), entonces se\(x\) reducirá (no se deslizará tan lejos si hay más fricción en el plano horizontal).
- Si aumentamos\(\theta\), el numerador será más grande, por lo que\(x\) aumentará (el bloque se acelerará más abajo una pendiente más pronunciada y terminará más allá).
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Un regalo se coloca en reposo en un plano que está inclinado, a una distancia\(L\) from the bottom of the incline, much like the box in Example 6.2.1 above. At the bottom of the incline, the box is determined to have a speed \(v\). If the box is instead released from a distance of \(4L\) from the bottom of the incline, what will its speed at the bottom of the incline be?
- \(v\)
- \(2v\)
- \(4v\)
- depende del coeficiente de fricción entre el presente y el plano.
Modelado de situaciones donde las fuerzas cambian de magnitud
Hasta el momento, los modelos que hemos considerado involucraron fuerzas que se mantuvieron constantes en magnitud. En muchos casos, las fuerzas ejercidas sobre un objeto pueden cambiar de magnitud y dirección. Por ejemplo, la fuerza ejercida por un resorte cambia a medida que el resorte cambia de longitud o la fuerza de arrastre cambia a medida que el objeto cambia de velocidad. En estos casos, aunque el objeto sufra un movimiento lineal, necesitamos dividir el movimiento en muchos segmentos pequeños sobre los cuales podemos suponer que las fuerzas son constantes. Si las fuerzas cambian continuamente, tendremos que romper el movimiento en un número infinito de segmentos y usar cálculo.
Considera el bloque de masa\(m\) que se muestra en la Figura\(\PageIndex{5}\), el cual se desliza a lo largo de una superficie horizontal sin fricción y tiene una fuerza horizontal\(\vec F(x)\) ejercida sobre ella. La fuerza tiene una magnitud diferente en los tres segmentos de longitud\(\Delta x\) que se muestran. Si el bloque inicia en el\(x=x_0\) eje de posición con velocidad\(v_0\), podemos encontrar, por ejemplo, su velocidad en posición\(x_3=3\Delta x\), después de que el bloque viajara a través de los tres segmentos.
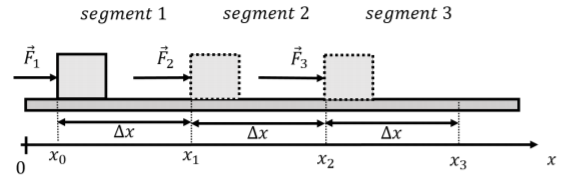
La fuerza horizontal,\(\vec F\), ejercida sobre el bloque puede escribirse\[\begin{aligned} \vec F (x)= \begin{cases} F_1\hat x & x<\Delta x \quad \text{(segment 1)}\\ F_2\hat x & \Delta x \leq x< 2\Delta x \quad \text{(segment 2)}\\ F_3\hat x & 2\Delta x \leq x\quad \text{(segment 3)} \end{cases}\end{aligned}\] como: ya que depende de la ubicación del bloque. Para encontrar la velocidad del bloque al final del tercer segmento, podemos modelar cada segmento por separado. Las fuerzas ejercidas sobre el bloque son las mismas en cada segmento:
- \(\vec F_g\), su peso, con magnitud\(mg\).
- \(\vec N\), una fuerza normal ejercida por el suelo.
- \(\vec F(x)\), una fuerza aplicada que cambia de magnitud con la posición y es diferente en los tres segmentos diferentes.
Las fuerzas se ilustran en el diagrama de cuerpo libre que se muestra en la Figura\(\PageIndex{7}\).
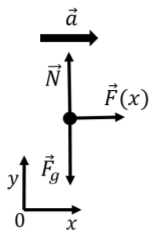
La Segunda Ley de Newton puede ser utilizada para determinar la aceleración del bloque para cada uno de los tres segmentos, ya que las fuerzas son constantes dentro de un segmento. Para los tres segmentos, el\(y\) componente de la Segunda Ley de Newton apenas nos dice que la fuerza normal ejercida por el suelo es igual en magnitud al peso del bloque. El\(x\) componente de la Segunda Ley de Newton da la aceleración:\[\begin{aligned} \sum F_x = F_i = ma_i\end{aligned}\] donde hemos utilizado el índice\(i\) para indicar en qué segmento se encuentra el bloque (\(i\)puede ser 1, 2 o 3). La aceleración del bloque en segmento\(i\) viene dada por:\[\begin{aligned} a_i = \frac{F_i}{m}\end{aligned}\] Si la velocidad del bloque está\(v_0\) al inicio del segmento 1 (\(x=x_0\)), podemos encontrar su velocidad al final del segmento 1 (\(x=x_1\)),\(v_1\), usando cinemática y el hecho de que la aceleración en el segmento 1 es\(a_1\): Ahora\[\begin{aligned} v_1^2-v_0^2 &= 2a_1(x_1 - x_0)\\ v_1^2 &=v_0^2+ 2a_1\Delta x\\ \therefore v_1^2 &=v_0^2+2\frac{F_1}{m}\Delta x\end{aligned}\] podemos encontrar fácilmente la velocidad al final del segmento 2 (\(x=x_2\))\(v_2\), ya que conocemos la velocidad al inicio del segmento 2 (\(x_1\), \(v_1\)) y la aceleración\(a_2\):\[\begin{aligned} v_2^2 -v_1^2 &= 2a_2(x_2 - x_1)\\ \therefore v_2^2 &= v_1^2 + 2a_2\Delta x\\ &=v_0^2+ 2\frac{F_1}{m}\Delta x + 2\frac{F_2}{m}\Delta x\end{aligned}\] Es fácil demostrar que la velocidad al final del tercer segmento es:\[\begin{aligned} v_3^2 = v_0^2+ 2\frac{F_1}{m}\Delta x + 2\frac{F_2}{m}\Delta x +2\frac{F_3}{m}\Delta x\end{aligned}\] Si hubiera\(N\) segmentos, siendo la fuerza diferente en cada segmento, podríamos usar la notación de suma para escribir:\[\begin{aligned} v_N^2 &= v_0^2 + 2\sum_{i=1}^{i=N} \frac{F_i}{m}\Delta x\end{aligned}\] Finalmente, si la magnitud de la fuerza variara continuamente en función de\(x\),\(\vec F(x)\), modelaríamos esto tomando segmentos cuya longitud,\(\Delta x\), tiende a cero (y necesitaríamos un número infinito de tales segmentos). Por ejemplo, si quisiéramos conocer la velocidad del objeto en posición a\(x=X\) lo largo del\(x\) eje, con una fuerza que estaba dada por\(\vec F(x)=F(x)\hat x\), si el objeto comenzaba en posición\(x_0\) con velocidad\(v_0\), tomaríamos el siguiente límite:\[\begin{aligned} v^2 = v_0^2 + \lim_{\Delta x \to 0} 2\sum_{i=1}^{i=N} \frac{F(x)}{m}\Delta x\end{aligned}\] donde\(\Delta x = \frac{X}{N}\) para que como\(\Delta x\to 0\),\(N\to\infty\). Por supuesto, las integrales son la herramienta exacta que nos permite evaluar la suma en este límite:\[\begin{aligned} \lim_{\Delta x \to 0} 2\sum_{i=1}^{i=N} \frac{F_i}{m}\Delta x =2 \int_{x_0}^{X}\frac{F(x)}{m}dx \end{aligned}\] y la velocidad en posición\(x=X\) viene dada por:\[\begin{aligned} v^2 = v_0^2 + 2 \int_{x_0}^{X}\frac{F(x)}{m}dx \end{aligned}\] Naturalmente, podemos encontrar el resultado anterior partiendo directamente del cálculo. Si el componente de la fuerza (neta) en la\(x\) dirección viene dada por\(F(x)\), entonces la aceleración viene dada por\(a(x) = \frac{F(x)}{m}\). La velocidad está relacionada con la aceleración: No\[\begin{aligned} a(x) &= \frac{dv}{dt}\\ \therefore dv &= a(x)dt\\\end{aligned}\] podemos simplemente integrar la última ecuación para encontrarla\(v=\int a(x)dt\) porque la aceleración se da en función de la posición\(a(x)\), y no en función del tiempo,\(t\). Por lo tanto, no podemos simplemente tomar la integral\(t\) y, en cambio, debemos “cambiar las variables” para tomar la integral\(x\). \(x\)y\(t\) se relacionan a través de la velocidad:\[\begin{aligned} v &= \frac{dx}{dt}\\ \therefore dt &= \frac{1}{v}dx\end{aligned}\] Podemos escribir así:\[\begin{aligned} dv &= a(x)dt = a(x)\frac{1}{v}dx \\\end{aligned}\] La ecuación anterior se llama una “ecuación diferencial separable”, que también se puede escribir:\[\begin{aligned} \frac{dv}{dx}=\frac{1}{v}a(x)\end{aligned}\] Esto se llama ecuación diferencial porque relaciona la derivada de una función (la derivada de\(v\) con respecto a\(x\), a la izquierda) a la función misma (\(v\)aparece también a la derecha). La ecuación diferencial es “separable”, porque podemos separar todas las cantidades que dependen de\(v\) y de diferentes\(x\) lados de la ecuación:\[\begin{aligned} vdv = a(x)dx\end{aligned}\] Esta última ecuación dice que\(vdv\) es igual a\(a(x)dx\). Recuerde que\(dx\) es la longitud de un segmento muy pequeño en\(x\), y ese\(dv\) es el cambio de velocidad sobre ese segmento muy pequeño. Dado que los términos de la izquierda y la derecha son iguales, si sumamos (integramos) la cantidad\(vdv\) sobre muchos segmentos, esa suma debe ser igual a la suma (integral) de la cantidad\(a(x)dx\) sobre los mismos segmentos. Escojamos esos segmentos de tal manera que para el inicio del primer intervalo la posición y la velocidad sean\(x_0\) y\(v_0\), respectivamente, y la posición y velocidad al final del último segmento sean\(X\) y\(V\), respectivamente. Entonces debemos tener eso:\[\begin{aligned} \int_{v_0}^{V}vdv&=\int_{x_0}^{X}a(x)dx\\ \frac{1}{2}V^2 - \frac{1}{2}v_0^2 &= \int_{x_0}^{X}a(x)dx\\ \therefore V^2 &= v_0^2 + 2\int_{x_0}^{X}a(x)dx\\\end{aligned}\] que es lo mismo que encontramos antes. Si la aceleración es constante, recuperamos nuestra fórmula de la cinemática:\[\begin{aligned} V^2 &= v_0^2+ 2\int_{x_0}^{X}adx\\ &=v_0^2+ 2a(X-x_0)\\ \therefore V^2- v_0^2 &= 2a(X-x_0)\end{aligned}\]
Ejemplo\(\PageIndex{2}\)
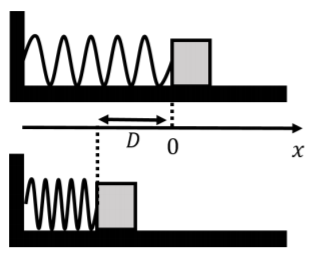
Un bloque de masa\(m\) can slide freely along a frictionless surface. A horizontal spring, with spring constant, \(k\), is attached to a wall on one end, while the other end can move freely, as shown in Figure \(\PageIndex{8}\). A coordinate system is defined such that the \(x\) axis is horizontal and the free end of the spring is at \(x=0\) when the spring is at rest. The block is pushed against the spring so that the spring is compressed by a distance \(D\). The block is then released. What speed will the block have when it leaves the spring?
Solución:
Como recuerdas, la fuerza ejercida por un resorte depende de la compresión o extensión del resorte y viene dada por la Ley de Hooke:\[\begin{aligned} \vec F(x) = -kx\hat x\end{aligned}\] donde\(x\) está la posición del extremo libre del muelle y\(x=0\) corresponde a que el resorte esté en reposo. En nuestro caso, cuando el borde del bloque se ubica en\(x_0=-D\) (el resorte está comprimido), la fuerza está así en la\(x\) dirección positiva (ya que\(x_0\) es un número negativo).
Las fuerzas en el bloque son:
- \(\vec F_g\), su peso, con magnitud\(mg\).
- \(\vec N\), una fuerza normal ejercida por el suelo.
- \(\vec F(x)\), la fuerza del resorte.
Dado que el bloque no se mueve verticalmente, la magnitud de la fuerza normal debe ser igual al peso\(N=mg\), ya que estas son las únicas fuerzas con componentes en la dirección vertical. El\(x\) componente de la Segunda Ley de Newton nos da la aceleración del bloque (que depende de\(x\)):\[\begin{aligned} \sum F_x = -kx &= ma(x)\\ \therefore a(x)&=-\frac{k}{m}x\end{aligned}\] Nuevamente, recordemos que si\(x\) es negativo, entonces la aceleración será en la dirección positiva. Dado que este escenario es exactamente el mismo que describimos anteriormente en el texto, es decir, una fuerza que varía continuamente con la posición, podemos aplicar la fórmula que encontramos anteriormente para determinar la velocidad después de que se haya aplicado una fuerza variable de posición\(x=x_0\) a posición \(x=X\):\[\begin{aligned} V^2 &= v_0^2 + 2\int_{x_0}^{X}a(x)dx\end{aligned}\]\(V\) es la velocidad final que nos gustaría encontrar,\(v_0=0\) porque el bloque comienza en reposo, y\(x_0=-D\) es la posición inicial del bloque. \(X\)es la posición a lo largo del\(x\) eje donde el bloque sale del muelle.
Tenemos que pensar un poco en cuál\(X\) debería ser el valor de: cuando el resorte se comprime y el bloque se acelera, el resorte está empujando el bloque en la\(x\) dirección positiva. Una vez que\(x=0\) el bloque llega al muelle querría tirar del bloque hacia atrás, pero como no está unido al bloque, deja de ejercer una fuerza sobre el bloque en ese punto. El bloque deja así el muelle en\(x=0\), de manera que la posición final es\(X=0\). La velocidad del bloque cuando sale del muelle es así:\[\begin{aligned} V^2 &= v_0^2 + 2\int_{x_0}^{X}a(x)dx\\ &= 0 + 2\int_{-D}^{0}a(x)dx\\ &= 2\int_{-D}^{0}-\frac{k}{m}xdx\\ &= 2\left[ - \frac{k}{m}\frac{1}{2}x^2\right]_{-D}^{0}\\ &= \frac{k}{m}D^2\\ \therefore V &= \sqrt{\frac{k}{m}}D\end{aligned}\]
Discusión:
Este modelo para la velocidad del bloque cuando sale del muelle tiene sentido porque:
- La dimensión para la expresión for\(V\) es correcta (¡deberías comprobarlo!).
- Si el resorte se comprime más (mayor valor de\(D\)), entonces la velocidad será mayor.
- Si la masa es mayor (más inercia), entonces la velocidad final será menor.
- Si el resorte es más rígido (mayor valor de\(k\)), entonces la velocidad final será mayor.
Si has estudiado física antes, es posible que te hayas dado cuenta de que la velocidad se encuentra fácilmente por la conservación de la energía:\[\begin{aligned} \frac{1}{2}mV^2=\frac{1}{2}kD^2\end{aligned}\] lo que da el mismo valor para\(V\). Como veremos en un capítulo posterior, la energía cinética y potencial se definen tal como son, precisamente porque hace que el uso de la conservación de energía sea equivalente al uso de fuerzas como acabamos de hacer.
Ejemplo\(\PageIndex{3}\)
Un objeto de masa\(m\) is released from rest out of a helicopter. The drag (air-resistance) on the object can be modeled as having a magnitude given by \(bv\), where \(v\) is the speed of the object and \(b\) is a constant of proportionality. How does the velocity of the object depend on time?
Solución:
A medida que el objeto cae por el aire, las fuerzas ejercidas sobre el objeto son:
- \(F_g\), su peso, con magnitud\(mg\), ejercido hacia abajo.
- \(F_d\), la fuerza de arrastre, con magnitud\(bv\), ejercida hacia arriba.
Dado que el objeto caerá en línea recta, este es un problema unidimensional, y podemos elegir el\(x\) eje para que sea vertical, con positivo\(x\) apuntando hacia abajo, y el origen ubicado donde se liberó el objeto. El objeto tendrá así una aceleración positiva y se moverá en la\(x\) dirección positiva con esta elección del sistema de coordenadas. Esto se ilustra en el diagrama de cuerpo libre en la Figura\(\PageIndex{9}\).
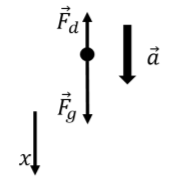
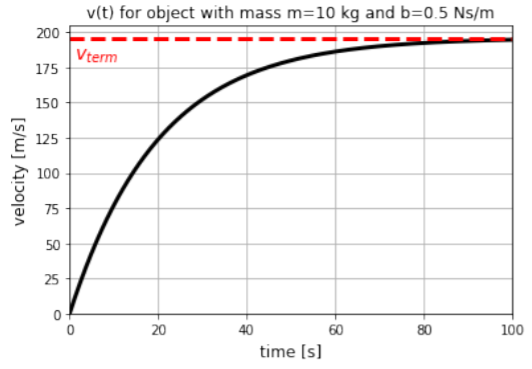
La Segunda Ley de Newton para el objeto da:\[\begin{aligned} \sum F_x = F_g - F_d &= ma\\ mg - bv &= ma\\ \therefore a &= g-\frac{b}{m}v \end{aligned}\] En este caso, la aceleración depende explícitamente de la velocidad más que de la posición, como teníamos antes. Sin embargo, podemos usar la misma metodología para encontrar cómo cambia la velocidad con el tiempo. Primero, podemos señalar que la aceleración es cero si: Es decir, una vez\[\begin{aligned} g-\frac{b}{m}v &=0\\ \therefore v = \frac{mg}{b}\end{aligned}\] que el objeto alcanza una velocidad de\(v_{term}=mg/b\), dejará de acelerar, es decir, alcanzará la “velocidad terminal”. Tenga en cuenta que esta es la misma condición que requerir que la fuerza de arrastre (\(bv\)) tenga la misma magnitud que el peso (\(mg\)).
Escribiendo la aceleración como\(a=\frac{dv}{dt}\), podemos escribir:\[\begin{aligned} \frac{dv}{dt} &= \left(g-\frac{b}{m}v \right)\end{aligned}\] que de nuevo, es una ecuación diferencial separable, en la que podemos escribir los términos de los que dependen\(v\) y los que\(t\) dependen de lados separados del signo igual:\[\begin{aligned} \frac{dv}{g-\frac{b}{m}v}&= dt\\ \frac{dv}{v-\frac{mg}{b}}&= -\frac{b}{m}dt\\\end{aligned}\] donde re- arregló la ecuación en la segunda línea para que fuera más fácil de integrar en el siguiente paso. Podemos encontrar la velocidad\(v(t)\), en algún momento,\(t\), al afirmar que\(v=0\) en\(t=0\) y tomando las integrales (suma) en ambos lados. Nuevamente, estamos modelando el movimiento como compuesto por un gran número de segmentos muy pequeños donde las cantidades a ambos lados de la ecuación son las mismas. Así, si sumamos (integramos) esas cantidades sobre todos los mismos segmentos, el lado izquierdo y derecho de las ecuaciones seguirán siendo iguales entre sí:\[\begin{aligned} \int_0^{v(t)}\frac{dv}{v-\frac{mg}{b}} &= -\int_0^t\frac{b}{m} dt\\ \left[\ln\left(v-\frac{mg}{b} \right)\right]_0^{v(t)} &=-\frac{b}{m}t\\ \ln\left(v(t)-\frac{mg}{b} \right)-\ln\left(-\frac{mg}{b} \right)&=-\frac{b}{m}t\\ \ln\left( \frac{v(t)-\frac{mg}{b}}{-\frac{mg}{b}} \right)&=-\frac{b}{m}t\\\end{aligned}\] donde, en la última línea, usamos la propiedad que\(\ln(a)-\ln(b)=\ln(a/b)\). Al tomar el exponencial a cada lado de la ecuación (\(e^{\ln(x)}=x\)), podemos encontrar una expresión para la velocidad en función del tiempo:\[\begin{aligned} \frac{v(t)-\frac{mg}{b}}{-\frac{mg}{b}} &= e^{-\frac{b}{m}t}\\ v(t)-\frac{mg}{b} &= -\frac{mg}{b}e^{-\frac{b}{m}t}\\ \therefore v(t) &= \frac{mg}{b}-\frac{mg}{b}e^{-\frac{b}{m}t}\\ &=\frac{mg}{b}\left(1-e^{-\frac{b}{m}t}\right)\end{aligned}\]
Discusión:
Esta ecuación nos dice que la velocidad aumenta en función del tiempo, pero la tasa de aumento disminuye exponencialmente con el tiempo. En el momento\(t=0\), la velocidad es cero, como se esperaba. A medida que\(t\) se\(v\) acerca al infinito, se acerca\(\frac{mg}{b}\),, que es la velocidad terminal. La dependencia del tiempo de la velocidad se ilustra en la Figura\(\PageIndex{10}\).