7.1: Trabajo

Última actualización
Guardar como PDF

Page ID: 129494

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ejercicios de revisión

Sección A1.3 sobre el producto escalar.
Sección A2.3 sobre integrales.

Introducimos el concepto de trabajo como punto de partida para construir modelos utilizando energía en lugar de fuerzas. El trabajo es una cantidad escalar que pretende representar cómo una fuerza ejercida sobre un objeto a una distancia dada da como resultado un cambio en la velocidad de ese objeto. Primero introduciremos el concepto de trabajo realizado por una fuerza sobre un objeto, y luego veremos cómo el trabajo puede cambiar la cinemática del objeto. Esto es análogo a cómo primero definimos el concepto de fuerza, y luego vimos cómo la fuerza afecta el movimiento (usando la Segunda Ley de Newton, que conectaba el concepto de fuerza con la aceleración del objeto).

El trabajo realizado por una fuerza$\vec F$, sobre un objeto sobre un desplazamiento$\vec d$, se define como:

\[W = \vec F \cdot \vec d = Fd\cos\theta = F_xd_x+F_yd_y+F_zd_z\]

donde$\theta$ está el ángulo entre los vectores cuando se colocan cola a cola, como en la Figura 7.1.1. La dimensión del trabajo, fuerza veces desplazamiento, también se llama “energía”. La unidad S.I. para energía es el Joule (abreviado$\text{J}$) que es equivalente a$\text{Nm}$ o$\text{kg m}^{2}/\text{s}^{2}$ en unidades base.

Figura$\PageIndex{1}$: Al determinar el producto escalar$\vec F \cdot \vec d = F d\cos θ$,$θ$ es el ángulo entre los vectores cuando se colocan cola a cola.

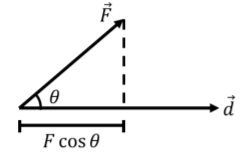
El trabajo “realizado” por la fuerza es el producto escalar del vector de fuerza y el vector de desplazamiento del objeto. Decimos que la fuerza “sí funciona” si se ejerce mientras el objeto se mueve (tiene un vector de desplazamiento) y de tal manera que el producto escalar de los vectores de fuerza y desplazamiento es distinto de cero. Una fuerza que es perpendicular al vector de desplazamiento de un objeto no funciona (ya que el producto escalar de dos vectores perpendiculares es cero). Una fuerza ejercida en la misma dirección que el desplazamiento hará un trabajo$\cos\theta $ positivo (positivo), y una fuerza en la dirección opuesta al desplazamiento hará trabajo negativo ($\cos\theta $negativo). Como veremos, el trabajo positivo corresponde a aumentar la velocidad del objeto, mientras que el trabajo negativo corresponde a disminuir su velocidad. Ningún trabajo corresponde a ningún cambio en la velocidad (pero podría corresponder a un cambio en la velocidad).

Ejercicio$\PageIndex{1}$

Un péndulo de longitud$R$ consiste en una masa conectada a una cuerda (Figura$\PageIndex{2}$). La cuerda ejerce una fuerza de tensión$\vec F_T$ sobre la masa. ¿Cuál es el trabajo que realiza la tensión cuando el péndulo se balancea a través de un ángulo$\theta $?

Figura$\PageIndex{2}$: Un péndulo oscila en un ángulo$\theta$.

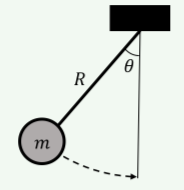
$W=F_{T}R\theta$
$W=F_{T}R(1-\cos\theta)$
La tensión no funciona en la masa.

Contestar

Quizás te sienta tentado a preguntar: “¿Por qué trabajar? ¿Por qué no otra cosa? ¿Por qué ese producto escalar en particular? ¿Cómo podríamos haber pensado en eso?”. En general, parece arbitrario que introduzcamos la cantidad “trabajo” y luego encontremos que conduce a una forma conveniente de construir modelos. Sin embargo, ¡no solo sacamos esta cantidad de la nada! Muchos teóricos, a lo largo de muchos años, probaron todo tipo de cantidades y formas de reformular la Teoría de Newton que no fueron útiles. Las cantidades que lo convierten en libros de texto son las que resultaron útiles. También debes tener en cuenta que, al igual que la fuerza, el trabajo es una herramienta matemática “inventada” que es útil para describir el mundo que nos rodea. No existe el trabajo o la energía; solo son herramientas matemáticas útiles.

Trabajar en una dimensión.

El trabajo involucra vectores, por lo que primero podemos examinar el concepto en una dimensión, antes de extenderlo a dos y tres dimensiones. Podemos elegir$x$ como coordenada en una dimensión, de modo que todos los vectores solo tengan un$x$ componente. Podemos escribir un vector de fuerza como$\vec F=F\hat x$, donde$F$ está el$x$ componente de la fuerza (que podría ser positivo o negativo). Un vector de desplazamiento puede escribirse como$\vec d = d \hat x$, donde de nuevo,$d$ es el$x$ componente del desplazamiento, y puede ser positivo o negativo. En una dimensión, el trabajo es así:

$ W = \vec F \cdot \vec d = (F\hat x) \cdot ( d\hat x ) = Fd (\hat x\cdot\hat x)=Fd$

donde$\hat x \cdot \hat x = 1$. Consideremos, por ejemplo, el trabajo realizado por una fuerza,, sobre una caja$\vec F$, a medida que la caja se mueve a lo largo del$x$ eje de una posición$x=x_0$ a otra$x=x_1$, como se muestra en la Figura$\PageIndex{3}$.

Figura$\PageIndex{3}$: Una fuerza,$\vec F$, ejercida sobre un objeto a medida que se mueve de una posición$x=x_0$ a otra$x=x_1$.

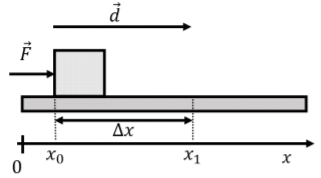
Podemos escribir la longitud del vector de desplazamiento como$||\vec d|| =d= \Delta x = x_1-x_0$. El trabajo realizado por la fuerza viene dado por:

$W = \vec F \cdot \vec d = F\hat x\cdot \Delta x\hat x =F\Delta x =F(x_1-x_0)$

que es una cantidad positiva, ya que$x_1 > x_0$, con nuestra elección de sistema de coordenadas.

Ejercicio$\PageIndex{2}$

Una fuerza constante en la$x$ dirección positiva,$\vec F$, actúa sobre una caja, como en la Figura$\PageIndex{3}$. Considera el trabajo realizado por a$\vec F$ medida que la caja se mueve de$x_1$ a$x_0$. ¿Cómo se compara con el trabajo realizado$\vec F$ al pasar de$x_0$ a$x_1$ (que calculamos anteriormente)?

$\vec F$no funciona en la caja cuando se mueve de$x_0$ a$x_1$.
El trabajo tiene la misma magnitud que antes, pero ahora el trabajo es negativo.
El trabajo realizado por$\vec F$ es el mismo en ambos casos.

Contestar

Trabajo en una dimensión - fuerza variable

Supongamos que en lugar de una fuerza constante$\vec F$,, tenemos una fuerza que cambia con la posición$\vec F(x)$,, y puede tomar tres valores diferentes entre$x=x_0$ y$x=x_3$:

\ begin {align*}\ vec F (x) =\ begin {cases} F_1\ hat x & x<\ Delta x\\ F_2\ hat x &\ Delta x\ leq x< 2\ Delta x\\ F_3\ hat x & 2\ Delta x\ leq x\ end {cases}\ end {align*}

como se ilustra en la Figura$\PageIndex{3}$, que muestra la fuerza sobre un objeto a medida que se mueve de una posición$x=x_0$ a otra$x=x_3$$, a lo largo de tres vectores de desplazamiento (iguales),$\vec d_1=\vec d_2=\vec d_3=\Delta x \hat x$

Figura$\PageIndex{4}$: Una fuerza variable,$\vec F(x)$, ejercida sobre un objeto a medida que se mueve de una posición$x=x_0$ a otra$x=x_3$.

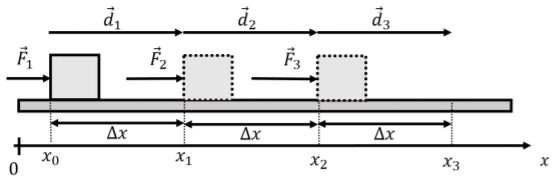
El trabajo total realizado por la fuerza sobre los tres desplazamientos separados es la suma del trabajo realizado sobre cada desplazamiento:

\ begin {alinear*} W^ {tot} &=W_1+W_2+W_3\\ &=\ vec F_1\ cdot\ vec d_2+\ vec F_2\ cdot\ vec d_2+\ vec F_3\ cdot\ vec d_3\\ &= F_1\ Delta x +F_2\ Delta x + F_3\ Delta x\ final alinear*}

Si en lugar de$3$ segmentos tuviéramos$N$ segmentos y el$x$ componente de la fuerza tuviera los valores$N$ correspondientes$F_i$ en los$N$ segmentos, el trabajo total realizado por la fuerza sería:

\ begin {alinear*} W^ {tot} =\ suma_ {i=0} ^N\ vec F_i\ cdot\ Delta\ vec x\ final {alinear*}

donde introdujimos un vector$\Delta \vec x$ para ser el vector de longitud$\Delta x$ apuntando en la$x$ dirección positiva. En el límite donde$\vec F(x)$ cambia continuamente en función de la posición, tomamos el límite de un número infinito de segmentos infinitamente pequeños de longitud$dx$, y la suma se convierte en una integral:

\ begin {align} W^ {tot} =\ int_ {x_0} ^ {x_f}\ vec F (x)\ cdot d\ vec x\ end {align}

donde el trabajo se calculó en ir de$x=x_0$ a$x=x_f$, y$d\vec x=dx\hat x$ es un vector de desplazamiento infinitamente pequeño (de longitud$dx$) en la$x$ dirección positiva.

Ejemplo$\PageIndex{1}$

Se presiona un bloque contra el extremo libre de un resorte horizontal con constante de resorte$k$, para comprimir el resorte por una distancia$D$ relativa a su longitud de reposo, como se muestra en la Figura$\PageIndex{5}$. El otro extremo del muelle está fijado a una pared. ¿Cuál es el trabajo que realiza la fuerza del resorte sobre el bloque al pasar de$x=-D$ a$x=0$? ¿Cuál es el trabajo realizado por el bloque en el muelle sobre el mismo desplazamiento?

Figura$\PageIndex{5}$: Un bloque se presiona contra un resorte horizontal para comprimir el resorte una distancia$D$ relativa a su longitud de reposo.

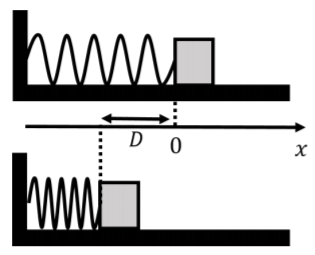
Solución:

La fuerza ejercida por el resorte sobre el bloque cambia continuamente con la posición, según la ley de Hooke:\ begin {align*}\ vec F (x) = -kx\ hat x\ end {align*}

y apunta en la$x$ dirección positiva cuando el extremo del resorte tiene una posición negativa $x$ (con nuestra elección de coordenadas ilustrada en la Figura$\PageIndex{5}$, donde el origen se encuentra en la longitud restante del resorte). Para calcular el trabajo realizado por la fuerza, sumamos el trabajo realizado por la fuerza sobre muchos desplazamientos infinitesimalmente pequeños$d\vec x$ (utilizando una integral):

\ begin {align*} W &=\ int_ {-D} ^0\ vec F (x)\ cdot d\ vec x\\ &=\ int_ {-D} ^0 (-kx\ hat x)\ cdot (dx\ hat x)\ &=\ int_ {-D} ^0 -kxdx (\ hat x\ cdot\ hat x)\ =-\ int_ {-D} ^0 kx dx\\ &=-\ izquierda [\ frac {1} {2} kx^2\ derecha] _ {-D} ^0\\ &=\ frac {1} {2} kd^2\ end {align*}

Para determinar el trabajo que realizó el bloque en el muelle, necesitamos determinar la fuerza,$\vec F'(x)$, ejercida por el bloque sobre el resorte. Por la Tercera Ley de Newton, esto es igual en magnitud pero opuesto en dirección a la fuerza ejercida por el resorte sobre el bloque:

\ begin {align*}\ vec F' (x) = -\ vec F (x) = kx\ hat x\ end {alinear*}

El trabajo realizado por el bloque en el muelle sobre el mismo desplazamiento es:

\ begin {align*} W' &=\ int_ {-D} ^0\ vec F' (x)\ cdot d\ vec x\\ &=\ int_ {-D} ^0 (kx\ hat x)\ cdot (dx\ hat x)\ &=\ int_ {-D} ^0 kx dx=-\ frac {1} {2} kd^2\\\ final {alinear*}

lo cual es negativo. Esto tiene sentido porque la fuerza ejercida por el bloque sobre el resorte está en la dirección opuesta a la dirección del desplazamiento, por lo que el trabajo debe ser negativo.

Trabajo en múltiples dimensiones

Primero, consideremos el trabajo realizado por una fuerza$\vec F$ al tirar de una caja sobre un desplazamiento$\vec d$, en el caso en que la fuerza se dirija en un ángulo$\theta$ por encima de la horizontal, como se muestra en la Figura$\PageIndex{6}$, y el desplazamiento es a lo largo del$x$ eje (o mejor dicho, elegimos el$x$ eje para ser paralelo al desplazamiento).

Figura$\PageIndex{6}$: Una fuerza,$\vec F$, ejercida sobre un objeto a medida que se mueve de una posición$x=x_0$ a otra$x=x_1$.}

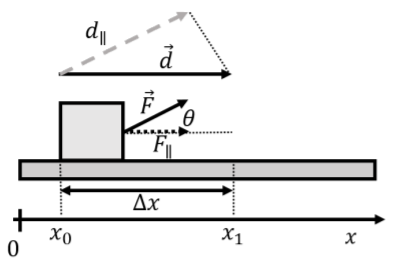
El trabajo realizado por la fuerza viene dado por:

\ begin {alinear*} W =\ vec F\ cdot\ vec d &= Fd\ cos\ theta\\ &= F_ {\ paralelo} d\\ &= Fd_ {\ paralelo}\\\ final {alinear*}

donde destacamos el hecho de que el producto escalar “escoge” componentes de vectores que son paralelos entre sí. $F_{\parallel} = F\cos\theta$es el componente de$\vec F$ que es paralelo a$\vec d$, y$d_{\parallel}=d\cos\theta$ es el componente de$\vec d$ que es paralelo a$\vec F$. Estos también se muestran en la Figura$\PageIndex{6}$.

Ejercicio$\PageIndex{3}$

Brent y Dean tiran de dos cajas usando cuerdas que hacen el mismo ángulo por encima de la horizontal y con la misma fuerza. La magnitud del desplazamiento de las cajas es la misma, pero la caja de Dean se mueve horizontalmente en el suelo mientras que la caja de Brent sube por una rampa sin fricción que es paralela a la cuerda utilizada para tirar de la caja. ¿Quién trabajó más en la caja?

Dean porque hay fricción entre su caja y el suelo.
Brent.
Hicieron la misma cantidad de trabajo.

Contestar

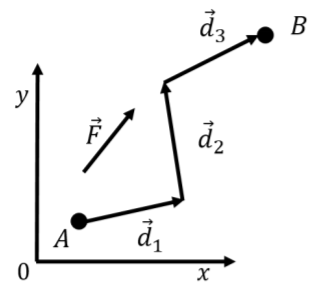
En general, si un objeto se mueve a lo largo de una trayectoria arbitraria, no podemos elegir el eje $x$ para que sea paralelo al desplazamiento o a la fuerza. Si la trayectoria se puede subdividir en segmentos rectos sobre los cuales la fuerza es constante, como en la Figura$\PageIndex{7}$, podemos calcular el trabajo realizado por la fuerza sobre cada segmento y sumar el trabajo realizado en cada segmento juntos para obtener el trabajo total realizado por la fuerza. Obsérvese que, en general, el trabajo realizado por una fuerza a medida que un objeto se mueve de una posición a otra depende de la trayectoria particular que se tomó entre las dos posiciones, ya que las diferentes trayectorias tendrán longitudes de diferencia.

Figura$\PageIndex{7}$: Trayectoria bidimensional arbitraria de un objeto desde$A$ hasta$B$ roto en tres segmentos rectos.

Ejemplo$\PageIndex{2}$

Comparar el trabajo realizado por la fuerza de fricción cinética en el deslizamiento de una caja a lo largo de una superficie horizontal de la posición$A$ (coordenadas$x_A, y_A$) a la posición$B$ (coordenadas$x_B, y_B$) utilizando los dos caminos diferentes representados en la Figura$\PageIndex{8}$. Supongamos que la masa de la caja es$m$ y que el coeficiente de fricción cinética entre la caja y el suelo es$\mu_k$.

Figura$\PageIndex{8}$: Dos posibles caminos para deslizar una caja de una posición$A$ a otra$B$, como se ve desde arriba.

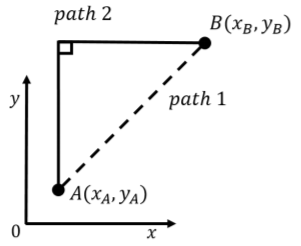
Solución:

La fuerza de fricción cinética está siempre en la dirección opuesta a la del movimiento. Así, independientemente del camino que se tome, la fuerza de fricción hará un trabajo negativo.

Primero calculemos el trabajo realizado por la fuerza de fricción cinética a lo largo del primer camino (la línea recta). La fuerza de fricción cinética tendrá una magnitud:\ begin {align*} f_k =\ mu_k N =\ mu_k mg\ end {align*}

La fuerza normal tendrá la misma magnitud que el peso debido a que la caja no se mueve (acelerando) en la dirección perpendicular al$xy$ plano. El vector de desplazamiento de$A$ a se$B$ puede escribir como:\ begin {align*}\ vec d &= (x_b-x_a)\ hat x + (Y_b-y_a)\ hat y\\\ por lo tanto ||\ vec d|| &=d=\ sqrt {(x_b-x_a) ^2 - (Y_b-y_a) ^2}\ end {align*}

La fuerza de fricción cinética estará en la dirección opuesta al vector de desplazamiento, por lo que el ángulo entre los dos vectores es$180^{\circ}(\cos\theta=-1)$. El trabajo realizado por la fuerza de fricción cinética es así:\ begin {align*} W =\ vec f_k\ cdot\ vec d = f_k d\ cos\ theta = -\ mu_k mg\ sqrt {(x_b-x_a) ^2 - (Y_b-y_a) ^2}\ end {align*} y es negativo, como se esperaba.

Para la trayectoria 2, dividimos el movimiento en dos segmentos, con vectores de desplazamientos$\vec d_1$ (a lo largo$y$) y$\vec d_2$ (a lo largo$x$). Podemos escribir los dos vectores de desplazamiento como:

\ begin {align*}\ vec d_1 &= 0\ hat x + (Y_b-y_a)\ hat y\\\ por lo tanto ||\ vec d_1||&=d_1= (y_b-y_a)\\\ vec d_2 &= (x_b-x_a)\ hat x + 0\ hat y\\\ por lo tanto ||\ vec d_2||&=d_2= (_b-x_a)\\\ final {alinear*}

A lo largo de cada segmento, la fuerza de fricción cinética es antiparalela al desplazamiento (tenga en cuenta que la fuerza de fricción cambia de dirección sobre los dos segmentos), pero la magnitud es$f_k=\mu_kmg$. El trabajo realizado a lo largo del primer segmento es así:\ begin {align*} W_1 =\ vec f_k\ cdot\ vec d_1 = f_k d_1\ cos\ theta = -\ mu_k mg (Y_b-y_a)\ end {align*} El trabajo realizado a lo largo del segundo segmento es:\ begin {align*} W_2 =\ vec f_k\ cdot\ vec d_2 = f_k d_2\ cos\ theta = -\ mu_k mg (x_b-x_a)\ end {align*} Y el trabajo total realizado por la fuerza de fricción cinética sobre la segunda trayectoria es:\ begin {align*} W^ {tot} = W_1 + W_2 = -\ mu_k mg\ left ((x_b-x_a) + (Y_b-y_a)\ right)\ end {align*} que es más trabajo que lo que se hizo a lo largo de la trayectoria 1. Esto tiene sentido porque para ambos caminos, la fuerza de fricción tiene la misma magnitud y siempre está en la dirección opuesta del movimiento; así, cuanto más largo sea el camino, más trabajo se hará por la fuerza.

Ejemplo$\PageIndex{3}$

Una caja de masa$m$ se mueve desde el suelo a una mesa utilizando dos caminos diferentes, como se muestra en la Figura$\PageIndex{9}$. La mesa está a una$L$ distancia horizontal de donde comienza la caja y una altura$H$ por encima del piso. Compara el trabajo realizado por el peso de la caja a lo largo de los dos caminos posibles.

Figura$\PageIndex{9}$: Dos posibles caminos para mover una caja del piso a una mesa.

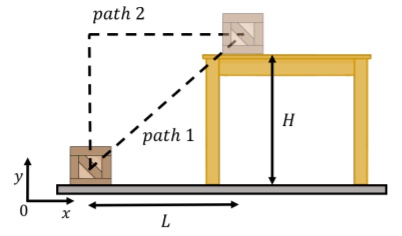
Solución:

Podemos utilizar un sistema de coordenadas tal que el origen coincida con la posición inicial de la caja. $x$es horizontal y$y$ vertical, como se muestra en la Figura$\PageIndex{9}$. El peso de la caja se puede escribir como:

\ start {alinear*}\ vec f_g = -mg\ hat y\ end {alinear*}

y apunta en la$y$ dirección negativa con una magnitud de$mg$. Para calcular el trabajo realizado por el peso a lo largo de la primera ruta, primero determinamos el vector de desplazamiento correspondiente,$\vec d$:

\ begin {align*}\ vec d = L\ hat x + H\ hat y\ end {align*}

y luego podemos determinar el trabajo:

\ begin {align*} W &=\ vec f_g\ cdot\ vec d = (-mg\ hat y)\ cdot (L\ hat x + H\ hat y)\\ &=F_xd_x+F_yd_y= (0) (L) + (-mg) (H)\\ &= -MGH\ end {align*}

A lo largo del camino 1, el trabajo realizado por el peso es negativo, y no depende de la distancia horizontal$L$. Ahora calculemos el trabajo realizado a lo largo del segundo camino, que dividimos en dos segmentos con vectores de desplazamiento$\vec d_1$ (vertical) y$\vec d_2$ (horizontal). Los vectores de desplazamiento son:

\ begin {align*}\ vec d_1 &= H\ hat y\\\ vec d_2 &= L\ hat x\ end {align*}

El trabajo realizado a lo largo del segmento vertical es:

\ begin {alinear*} W_1 &=\ vec f_g\ cdot\ vec d_1 = (-mg\ hat y)\ cdot (H\ hat y)\\ &=-MGH\ end {alinear*}

El trabajo realizado a lo largo del segmento horizontal es:

\ begin {align*} W_2 &=\ vec f_g\ cdot\ vec d_2 = (-mg\ hat y)\ cdot (L\ hat x)\\ &=0\ end {align*}

que es cero, porque la fuerza de gravedad siempre es vertical y por lo tanto perpendicular al vector de desplazamiento del segmento horizontal. El trabajo total realizado por el peso a lo largo del segundo camino es:

\ begin {align*} W^ {tot} = W_1 + W_2 = -MGH\ end {alinear*}

que es lo mismo que el trabajo realizado a lo largo del camino 1. Como veremos, cuando una fuerza es constante en magnitud y dirección, el trabajo que realiza sobre un objeto al pasar de una posición a otra es independiente del camino tomado. Este no fue el caso en el Ejemplo 7.1.2, porque la dirección de la fuerza de fricción cinética depende de la dirección del desplazamiento.

Ejercicio$\PageIndex{4}$

Clare y Amelia bajan dos diapositivas diferentes, como se muestra en la Figura$\PageIndex{10}$. Clare y Amelia tienen la misma masa y las correderas tienen los mismos coeficientes de fricción distintos de cero.

Figura$\PageIndex{10}$: Clare ($C$) y Amelia ($A$) bajan dos toboganes diferentes de la misma altura.

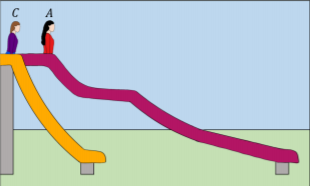
Para cada una de las siguientes fuerzas, decida si la fuerza: hace más trabajo en Clare, hace más trabajo en Amelia, o hace la misma cantidad de trabajo en ambas.

La fuerza de gravedad...
La fuerza de fricción...
La fuerza normal de la corredera...

Contestar: La gravedad hace la misma cantidad de trabajo en ambos, la fricción hace más trabajo en Amelia, y la fuerza normal hace la misma cantidad de trabajo en ambos (la fuerza normal hace trabajo cero, ya que siempre es perpendicular al desplazamiento).

El caso más general para el que podemos calcular el trabajo realizado por una fuerza es el caso cuando la fuerza cambia continuamente a lo largo de una trayectoria donde el desplazamiento también cambia de dirección continuamente. Esto se ilustra en la Figura$\PageIndex{11}$ que muestra una trayectoria arbitraria entre dos puntos$A$ y$B$, y una fuerza,$\vec F(\vec r)$, que depende de position ($\vec r$). En general, el trabajo realizado por la fuerza sobre un objeto que va de$A$ a$B$ dependerá del camino real que se tomó.

Figura$\PageIndex{11}$: Una trayectoria arbitraria entre dos puntos$A$ y$B$ con una fuerza que depende de la posición,$\vec F(\vec r)$.

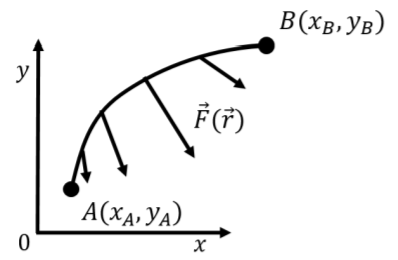
La estrategia para calcular el trabajo en el caso general es la misma: dividimos la trayectoria en pequeños segmentos rectos con vectores de desplazamiento$d\vec l$ (Figura$\PageIndex{12}$) donde asumimos que la fuerza es constante sobre el segmento. El trabajo total es la suma del trabajo sobre cada segmento:

\ begin {align} W =\ int_a^b\ vec F (\ vec r)\ cdot d\ vec l\ end {align}

Como es habitual, utilizamos el símbolo integral para indicar que es necesario tomar un número infinito de segmentos$d\vec l$ infinitamente pequeños para poder calcular la suma.

Figura$\PageIndex{12}$: Dividimos el camino en segmentos infinitesimalmente pequeños con vectores de desplazamiento$d\vec l$.

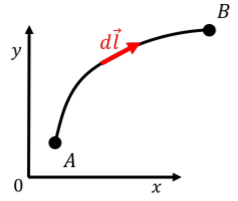
Cabe señalar que esta no es una integral como cualquier otra que hayamos visto hasta ahora: la integral no está sobre una sola variable de integración (usualmente usamos$x$), sino que es la integral (¡la suma!) sobre el camino específico que hemos elegido para ir de$A$ a$B$. Esto se denomina “integral de camino”, y generalmente es difícil de evaluar.

Ejemplo$\PageIndex{4}$

Figura$\PageIndex{13}$: Una trayectoria parabólica entre$A$ y$B$.

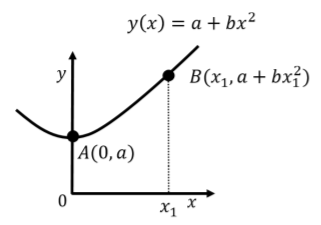
Una fuerza,$\vec F(\vec r) = \vec F(x,y) = F_x\hat x + F_y \hat y$, se ejerce sobre un objeto. El objeto comienza en posición$A$ y termina en posición$B$, a lo largo de una trayectoria parabólica$y(x) = a+bx^2$, como se representa en la Figura$\PageIndex{13}$. ¿Cuál es el trabajo que realiza la fuerza,$\vec F$, a lo largo de esta trayectoria?

Solución:

En este caso, la fuerza puede cambiar con la posición (si$F_x$ y no$F_y$ son constantes), y la dirección de la trayectoria cambia continuamente. Cuando rompemos el camino en pequeños segmentos$d\vec l$, necesitamos incorporar la ecuación de la parábola para incluir el hecho de que$d\vec l$ $ siempre debe ser tangente a la parábola. Considere un segmento pequeño a lo largo de la trayectoria y el vector de desplazamiento infinitesimal$d\vec l$ en ese punto, como en la Figura$\PageIndex{14}$.

Figura$\PageIndex{14}$: El vector de desplazamiento infinitesimal,$d\vec l$.

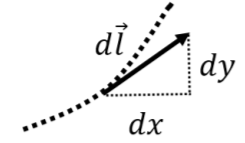
Podemos escribir los$y$ componentes$x$ y del vector como distancias infinitesimales$dx$ y$dy$, a lo largo de los$y$ ejes$x$ y, respectivamente. El vector$d\vec l$ se puede escribir así:

\ start {alinear*} d\ vec l = dx\ hat x + dy\ hat y\ end {alinear*}

El trabajo total realizado por la fuerza es entonces:

\ begin {align*} W &=\ int_a^b\ vec F (\ vec r)\ cdot d\ vec l\\ &=\ int_a^b (f_x\ hat x + f_y\ hat y)\ cdot (dx\ hat x + dy\ hat y)\\ &=\ int_a^b (f_x dx + f_ydy)\\\ por lo tanto W&=\ int_a^b f_x dx +\ int_a^b f_ydy\ end {alinear*}

donde en la última línea, simplemente usamos la propiedad de que la integral de una suma es la suma de las integrales correspondientes. En este punto, tenemos dos integrales sobre variables de integración ($x$y$y$) que son significativas. No obstante, aún no hemos utilizado el hecho de que nuestro camino es una parábola, y en general, esperamos que la forma del camino sea importante. Al decir que estamos integrando (o calculando la obra) sobre un camino específico, realmente lo estamos diciendo$x$ y no$y$ somos independientes; es decir, si conocemos el valor de$x$ en algún momento del camino, conocemos el valor correspondiente de$y$ ($y = a+bx^2$).

Dado que$x$ y no$y$ son independientes, podemos utilizar una “sustitución de variables” para expresar$y$ en términos de$x$, y$dy$ en términos de$dx$ $:

\ begin {align*} y (x) &= a + bx^2\\\ frac {dy} {dx} &= 2bx\\ por lo tanto dy &= 2bxdx\ end {align*}

Esto nos permite convertir la integral sobre$y$ en una integral sobre$x$, lo que también nos permite ser explícitos para los límites de la integral (en nuestro ejemplo, la integral va de$x=0$ a$x=x_1$):

\ begin {alinear*} W&=\ int_a^b f_x dx +\ int_a^b f_ydy\\ &=\ int_0^ {x_1} f_x dx +\ int_0^ {x_1} f_y (2bxdx)\\ &=\ int_0^ {x_1} (f_x + 2bxf_y) dx\ end {align*}

donde necesitaríamos saber cómo$F_x$ y$F_y$ depende$x$ y con el$y$ fin de evaluar realmente la integral.

Por ejemplo, si la fuerza fuera constante ($F_x$y$F_y$ constante), entonces el trabajo realizado a lo largo del camino parabólico sería:

\ begin {align*} W &=\ int_0^ {x_1} (F_x + 2bxF_y) dx\\ &=\ left [f_x x + bf_yx^2\ derecha] _0^ {x_1}\\ &=f_x x_0 + bf_yx_0^2\ end {align*}

Como mencionamos anteriormente, si la fuerza es constante en magnitud y dirección, entonces el trabajo realizado es independiente del camino. Podemos verificar esto fácilmente, usando el vector de desplazamiento$\vec d = x_1\hat x + bx_1^2 \hat y$:

\ begin {align*} W &=\ vec F\ cdot\ vec d = (f_x\ hat x+ f_y\ hat y)\ cdot (x_1\ hat x + bx_1^2\ hat y)\\ &=f_x x_1 + bf_yx_1^2\ end {align*}

como encontramos anteriormente.

Trabajo neto realizado

Hasta el momento, hemos considerado el trabajo realizado sobre un objeto por una sola fuerza. Si se ejerce más de una fuerza sobre un objeto, entonces cada fuerza puede hacer trabajo sobre el objeto, y podemos calcular el “trabajo neto” realizado en el objeto sumando el trabajo realizado por cada fuerza. Mostraremos que esto equivale a calcular primero la fuerza neta sobre el objeto,$F^{net}$ (es decir, la suma vectorial de las fuerzas sobre el objeto), y luego calcular el trabajo realizado por la fuerza neta.

Supongamos que tres fuerzas,$\vec F_1$,$\vec F_2$, y$\vec F_3$ se ejercen sobre un objeto a medida que se mueve de tal manera que su vector de desplazamiento es$\vec d$. El trabajo neto realizado sobre el objeto se muestra fácilmente como equivalente al trabajo realizado por la fuerza neta:

\ begin {align*} W^ {net} &= W_1 + W_2 + W_3\\ &=\ vec F_1\ cdot\ vec d +\ vec F_2\ cdot\ vec d +\ vec F_3\ cdot\ vec d\\ &= (F_ {1x} d_x+F_ {1y} d_y+f_ {1y} d_y+f_ {1z} d_z) + (F_ {2x} d_x+f_ {2y} d_y+f_ {2z} d_z) + (F_ {3x} d_x+f_ {3y} d_y+f_ {3z} d_z)\\ &= (F_ {1x} + F_ {2x} + F_ {3x}) d_x+ (F_ {1y} + F_ {2y} + F_ {3y}) d_y+ (F_ {1z} + F_ {2z} + F_ {3z}) d_z\\ &=\ vec F^ {net}\ cdot\ vec d\ end {align*}

donde$\vec F^{net} = \vec F_1 + \vec F_2 + \vec F_3$ esta la fuerza neta. El resultado se generaliza fácilmente a cualquier número de fuerzas, incluso si esas fuerzas cambian en función de la posición:

\ begin {align*} W^ {net} =\ int_a^b F^ {net} (\ vec r)\ cdot d\ vec l\ end {align*}

Ejemplo$\PageIndex{5}$

Empujas con una fuerza horizontal desconocida,$\vec F$, contra una caja de masa$m$ que se ubica en un plano inclinado que hace un ángulo $\ theta$ con respecto a la horizontal, como se muestra en la Figura$\PageIndex{15}$. El coeficiente de fricción cinética entre la caja y la inclinación es$\mu_k$. Empujas de tal manera que esas cajas se mueven a una velocidad constante subiendo la pendiente. ¿Cuál es el trabajo de red que se realiza en la caja si sube por la pendiente una distancia$d$?

Figura$\PageIndex{15}$: Una caja siendo empujada hacia arriba por una pendiente.

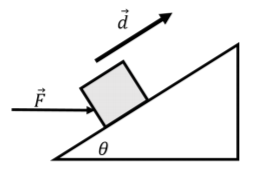
Solución:

Si bien la respuesta puede ser obvia, recorremos el largo camino al respecto y calculemos el trabajo realizado por cada fuerza, para luego sumarlos juntos para obtener el trabajo total realizado. Comenzamos por identificar las fuerzas ejercidas sobre la caja:

$\vec F$, la fuerza aplicada, de magnitud desconocida,$\vec F$.
$\vec F_g$, el peso de la caja, con magnitud$mg$.
$\vec N$, una fuerza normal ejercida por la inclinación.
$\vec f_k$, una fuerza de fricción cinética, con magnitud$\mu_k N$, que apunta en dirección opuesta a$\vec d$.

Estos se muestran en el diagrama de cuerpo libre en la Figura$\PageIndex{16}$, junto con nuestra elección del sistema de coordenadas, y el vector de desplazamiento.

Figura$\PageIndex{16}$: Diagrama de cuerpo libre para la caja en la pendiente.

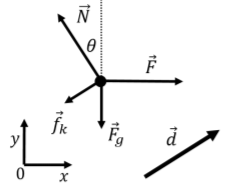
Con nuestra elección del sistema de coordenadas, el vector de desplazamiento viene dado por:

\ begin {align*}\ vec d = d (\ cos\ theta\ hat x +\ sin\ theta\ hat y)\ end {align*}

Antes de calcular el trabajo realizado por cada fuerza, necesitamos determinar la magnitud de la fuerza normal (y por lo tanto de la fuerza de fricción cinética). Dado que la caja se mueve a una velocidad constante, su aceleración es cero, por lo que la suma de las fuerzas debe ser cero. Escribir el$y$ componente de la Segunda Ley de Newton nos permite encontrar la magnitud de la fuerza normal:

\ begin {align*}\ suma f_y &= N\ cos\ theta -f_g - f_k\ sin\ theta = 0\\\ por lo tanto mg &= N\ cos\ theta-\ mu_kn\ sin\ theta = N (\ cos\ theta-\ mu_k\ sin\ theta)\\\ por lo tanto N &=\ frac {mg} {cos\ theta-\ mu_k\ sin\ theta}\ final {alinear*}

Escribir el$x$ componente de la Segunda Ley de Newton nos permite encontrar la magnitud de la fuerza desconocida$F$:

\ begin {align*}\ sum f_x &= F - N\ sin\ theta - f_k\ cos\ theta = 0\\\ por lo tanto F &= N\ sin\ theta+\ mu_kn\ cos\ theta = N (\ sin\ theta+\ mu_k\ cos\ theta)\\ &=mg\ frac {\ sin\ theta+\ mu_k\ cos\ theta} {\ cos\ theta-\ mu_k\ sin\ theta}\ fin {alinear*}

Ahora se procede a calcular el trabajo realizado por cada fuerza. El trabajo realizado por la fuerza normal es idéntico cero, ya que es perpendicular al vector de desplazamiento. El trabajo realizado por la fuerza aplicada,$\vec F = F\hat x$, es:

\ begin {align*} W_F &=\ vec F\ cdot\ vec d = (F\ hat x)\ cdot (d (\ cos\ theta\ hat x +\ sin\ theta\ hat y))\\ &=Fd\ cos\ theta=mg\ frac {\ sin\ theta+\ mu_k\ cos\ theta} {\ cos\ theta-\ mu_k\ sin\ theta} d\ cos\ theta\ fin {alinear*}

El trabajo realizado por la fuerza de la gravedad,$\vec F_g = -mg \hat y$, es:

\ begin {align*} w_g &=\ vec f_g\ cdot\ vec d = (-mg\ hat y)\ cdot (d (\ cos\ theta\ hat x +\ sin\ theta\ hat y))\\ &=-mgd\ sin\ theta\ end {align*}

El trabajo realizado por la fuerza de fricción,$\vec f_k$, señalando que$\vec f_k$ y$\vec d$ son antiparalelos:

\ begin {align*} w_f &=\ vec f_k\ cdot\ vec d = -f_kd = -\ mu_knd\\ &=-\ mu_k\ frac {mg} {\ cos\ theta-\ mu_k\ sin\ theta} d\ end {align*}

El trabajo neto realizado en la caja es así:

\ begin {align*} W^ {net} &=W_F + W_g + W_f\\ &=mg\ frac {\ sin\ theta+\ mu_k\ cos\ theta} {\ cos\ theta-\ mu_k\ sin\ theta} d\ cos\ theta-mgd\ sin\ theta -\ mu_k\ frac {mg} {cos\\ theta-\ mu_k\ sin\ theta} d\\ &=mgd\ izquierda (\ frac {\ sin\ theta+\ mu_k\ cos\ theta} {\ cos\ theta-\ mu_k\ sin\ theta}\ cos\ theta -\ sin\ theta -\ mu_k\ frac {1} {\ cos\ theta-\ mu_k\ sin\ theta}\ derecha)\\ &=mgd\ izquierda (\ frac {(\ sin\ theta+\ mu_k\ cos\ theta)\ cos\ theta -\ sin\ theta (\ cos\ theta-\ mu_k\ sin\ theta) -\ mu_k} {\ cos\ theta-\ mu_k\ sin\ theta}\ derecha)\\ &=mgd\ izquierda (\ frac {\ sin\ theta\ cos\ theta+\ mu_k\ cos^2\ theta -\ sin\ theta\ cos\ theta+\ mu_k\ sin^2\ theta -\ mu_k} {\ cos\ theta-\ mu_k\ sin\ theta}\ derecha)\\ &=mgd\ izquierda (\ frac {\ mu_k (\ cos^2\ theta+\ sin^2\ theta) -\ mu_k} {\ cos\ theta-\ mu_k\ sin\ theta}\ derecha)\\ &=0\ end {align*}

donde usamos el hecho de que$\cos^2\theta+\sin^2\theta=1$. ¡Así encontramos que el trabajo neto realizado en la caja es cero!

Discusión:

Por supuesto, esto tiene sentido, porque la fuerza neta sobre la caja es cero, ya que no se está acelerando, por lo que el trabajo neto realizado también es cero. Como consecuencia, o mejor dicho, por construcción, tenemos la condición de que si el trabajo neto realizado sobre un objeto es cero, entonces ese objeto no se acelere. Tenemos así una cantidad escalar (trabajo) que nos puede decir algo sobre si un objeto está cambiando de velocidad. En la siguiente sección, introducimos una nueva cantidad, “energía cinética”, para describir cómo cambia la velocidad de un objeto cuando el trabajo neto realizado no es cero. \ end {ejemplo}

Pensamientos de Olivia

Presta mucha atención a las palabras “on” y “by”. Hay algunas cosas sobre esto que pueden ser complicadas:

En el Ejemplo 7.1.5, se nos pidió que encontráramos el trabajo de red realizado en la caja. A veces, la pregunta no especificará que quiere que encuentres el trabajo de red, y solo dirá “¿Cuál es el trabajo realizado en la caja?” Cuando solo se le pide el trabajo realizado “en” un objeto, la pregunta es pedir implícitamente el trabajo de red realizado en el objeto.
El hecho de que el trabajo neto realizado en un objeto sea cero no significa que el trabajo realizado por cada una de las fuerzas sea cero. Esto puede parecer obvio, pero es fácil tropezarse con una prueba o examen. Si estás leyendo una pregunta sobre el trabajo y dice que el objeto se mueve a una velocidad constante, es tentador simplemente saltar adelante y decir que la obra debe ser igual a cero. Sin embargo, solo puedes decir esto si te está pidiendo el trabajo de red realizado en el objeto. Por ejemplo, en el Ejemplo 7.1.5, concluimos que como la caja se movía a velocidad constante, el trabajo neto era igual a cero. Pero si la pregunta te pidiera encontrar el trabajo realizado en la caja por gravedad, eso significaría algo diferente. El trabajo realizado por gravedad en este caso no es igual a cero (en realidad es negativo).
El trabajo realizado “sobre” un objeto no es lo mismo que el trabajo neto realizado “por” ese objeto. Por ejemplo, digamos que estás en un tira y afloja y tiras al otro equipo hacia ti, pero tú mismo no te mueves. El trabajo neto hecho en ti es cero, pero el trabajo realizado por ti no es cero. Entonces, cuando se habla de trabajo, siempre se debe indicar explícitamente si el trabajo se está realizando “sobre” el objeto o “por” el objeto.

Nota: La redacción no siempre será así, a veces dirá “¿Cuánto trabajo haces en la caja?” en lugar de “Cuánto trabajo haces tú en la caja”, así que siempre ten cuidado. Aún así, buscar palabras clave como “por” y “on” es un buen lugar para comenzar.

Ejercicio$\PageIndex{1}$

Una$2\text{kg}$ caja se asienta sobre una superficie horizontal. Se aplica una fuerza horizontal constante de$6\text{N}$ a la caja. La caja se mueve con una aceleración constante de$2\text{m/s}^{2}$. ¿Cuál de las siguientes tiene la mayor magnitud?

El trabajo realizado por la fuerza aplicada.
El trabajo realizado por fricción.
El trabajo neto realizado en la caja.

Contestar