7.2: La energía cinética y el teorema de energía de trabajo

En este punto, debe sentirse cómodo calculando el trabajo de red realizado sobre un objeto sobre el cual se ejercen varias fuerzas. Como vimos en la sección anterior, el trabajo neto realizado en un objeto está conectado a la aceleración del objeto; si la fuerza neta sobre el objeto es cero, entonces el trabajo neto realizado y la aceleración también son cero. En esta sección, derivamos una nueva cantidad, la energía cinética, que nos permite conectar el trabajo realizado sobre un objeto con su cambio de velocidad. Esto nos permitirá describir el movimiento usando solo cantidades escalares. Al igual que la definición de trabajo, la siguiente derivación parece “salir de la nada”. Recuerda, sin embargo, que los teóricos han intentado todo tipo de trucos matemáticos para reformular la Teoría de Newton, y esta es la que funcionó.

Consideremos el caso más general de un objeto de masa sobre el que\(m\) actúa una fuerza neta\(\vec F^{net}(\vec r)\), que puede variar en magnitud y dirección. Deseamos calcular el trabajo neto realizado sobre el objeto a medida que se mueve a lo largo de una trayectoria arbitraria entre dos puntos,\(A\) y\(B\), en el espacio, como se muestra en la Figura\(\PageIndex{1}\). La aceleración instantánea del objeto,\(\vec a\), se muestra junto con un “elemento del camino”,\(d\vec l\).

Figura\(\PageIndex{1}\): Un objeto que se mueve a lo largo de una trayectoria arbitraria entre puntos\(A\) y\(B\) que es actuado por una fuerza neta\(\vec F^{net}\).

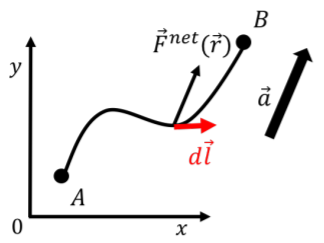
El trabajo neto realizado en el objeto se puede escribir:

\ begin {align*} W^ {net} =\ int_a^b F^ {net} (\ vec r)\ cdot d\ vec l\ end {align*}

y es en general una integral difícil de evaluar por un camino arbitrario. Nuestro objetivo es encontrar una manera de evaluar esta integral encontrando una función,\(K\), con la propiedad que:

\ begin {align*}\ int_a^b F^ {net} (\ vec r)\ cdot d\ vec l =K_B - K_A\ end {align*}

Es decir, sólo tendremos que evaluar\(K\) en los puntos finales del camino para determinar el valor de la integral. De esta manera, la función\(K\) es similar a un anti-derivado.

Para determinar la forma de la función\(K\), comenzamos por señalar que, utilizando la Segunda Ley de Newton, podemos escribir la integral para el trabajo en términos de la aceleración del objeto:

\ begin {align*}\ sum\ vec F &=\ vec F^ {net} = m\ vec a\\\ por lo tanto\ int_a^b F^ {net} (\ vec r)\ cdot d\ vec l &=\ int_a^b m\ vec a\ cdot d\ vec l =m\ int_a^b\ vec a\ cdot d\ vec l\ final {alinear*}

donde asumimos que la masa del objeto no cambia a lo largo del camino y así puede ser factorizada fuera de la integral. Considere el producto escalar de la aceleración\(\vec a\), y el elemento path,\(d\vec l=dx\hat x +dy\hat y + dz\hat z\), escrito en términos del vector de velocidad:

\ begin {align*}\ vec a & =\ frac {d\ vec v} {dt}\\\ por lo tanto\ vec a\ cdot d\ vec l &=\ frac {d\ vec v} {dt}\ cdot d\ vec l\\ &=\ left (\ frac {dv_x} {dt}\ hat x+\ frac {dv_y} {dt}\ hat y +\ frac {dv_z} {dt}\ hat z\ right)\ cdot (dx\ hat x +dy\ hat y + dz\ hat z)\\ &=\ frac {dv_x} {dt} dx+\ frac {dv_y} {dt} dy+\ frac {dv_z} {dt} dz\ end {align*}

Cualquiera de los términos de la suma se puede reorganizar de manera que la derivada de tiempo actúe sobre el elemento de path (\(dx, dy\), o\(dz\)) en lugar de la velocidad, por ejemplo:

\ begin {align*}\ frac {dv_x} {dt} dx =\ frac {dx} {dt} dv_x\ end {align*}

donde reconocemos eso\(\frac{dx}{dt} = v_x\). Así podemos escribir el producto escalar entre el vector de aceleración y el elemento path como:

\ begin {align*}\ vec a\ cdot d\ vec l&=\ frac {dv_x} {dt} dx+\ frac {dv_y} {dt} dy+\ frac {dv_z} {dt} dz\\ &=\ frac {dx} {dt} dv_x +\ frac {dy} {dt} dv_y+\ frac {z} {dt} dv_z\\ &=v_xdv_x + v_ydv_y + v_zdv_z\ end {align*}

La integral para el trabajo de red realizado puede escribirse como:

\ begin {align*} W^ {net} &=\ int_a^b F^ {net} (\ vec r)\ cdot d\ vec l =m\ int_a^b (v_xdv_x + v_ydv_y + v_zdv_z)\\ &=m\ int_a^b v_xdv_x +m\ int_a^b _ydv_y + m\ int_a^b v_zdv_z\ fin {alinear*}

que corresponde a la suma de tres integrales sobre los tres componentes independientes del vector de velocidad. Los componentes del vector de velocidad son funciones que cambian a lo largo de la trayectoria y tienen valores fijos en cada extremo de la trayectoria. Deje que el vector de velocidad del objeto en el punto\(A\) sea\(\vec v_A=(v_{Ax}, v_{Ay}, v_{Az})\) y el vector de velocidad en el punto\(B\) sea\(\vec v_B=(v_{Bx}, v_{By}, v_{Bz})\). La integral sobre, digamos, el\(x\) componente de la velocidad es entonces:

\ begin {alinear*} m\ int_a^b v_xdv_x &= m\ int_ {v_ {Ax}} ^ {v_ {Bx}} v_xdv_x= m\ izquierda [\ frac {1} {2} v_x^2\ derecha] _ {v_ {Ax}} ^ {v_ {Bx}}\\ &=\ frac 1} {2} m (v_ {Bx} ^2-v_ {Ax} ^2)\ final {alinear*}

Así podemos escribir la integral de la red de trabajo como:

\ begin {alinear*} W^ {net} &=m\ int_a^b v_xdv_x +m\ int_a^b v_ydv_y + m\ int_a^b v_zdv_z\\ &=\ frac {1} {2} m (v_ {Bx} ^2-v_ {Ax} ^2) +\ frac {1} {2} m (v_ {Por} ^2-v_ {Ay} ^2) +\ frac {1} {2} m (v_ {Bz} ^2-v_ {Az} ^2)\\ &=\ frac {1} {2} m (v_ {Bx} ^2+v_ {Por} ^2+v_ {Bz} ^2) -\ frac {1} {2} m (v_ {Ax} ^2+v_ {Ay} ^2+v_ {Az} ^2)\\ &=\ frac {1} {2} MV_b^2 -\ frac {1} {2} MV_a^2\ end {align*}

donde reconocimos que la magnitud (al cuadrado) de la velocidad viene dada por\(v_A^2 = v_{Ax}^2+v_{Ay}^2+v_{Az}^2\). Hemos llegado así a nuestro resultado deseado; es decir, hemos encontrado una función de velocidad,\(K(v)\), que cuando se evalúa en los extremos de la ruta nos permite calcular el trabajo neto realizado sobre el objeto sobre ese camino:

\[K(v)=\frac{1}{2}mv^{2}\]

Es decir, si conoces la velocidad al inicio del camino,\(v_A\), y la velocidad al final del camino\(v_B\), entonces el trabajo neto realizado sobre el objeto a lo largo del camino entre\(A\) y\(B\) viene dado por:

\[W^{net}=\Delta K=K(v_{B})-K(v_{a})\]

Llamamos a\(K(v)\) la “energía cinética” del objeto. Podemos decir que el trabajo neto realizado en un objeto al pasar de a\(B\) es igual\(A\) a su cambio en la energía cinética (energía cinética final menos energía cinética inicial). Es importante señalar que definimos la energía cinética de manera que sea igual al trabajo neto realizado. Es posible que ya hayas visto la energía cinética de pasadas introducciones a la física como una cantidad que se acaba de dar; aquí, en cambio derivamos una función que tiene la propiedad deseada de ser igual al trabajo neto realizado y la llamamos “energía cinética”.

La relación entre el trabajo neto realizado y el cambio en la energía cinética se denomina “Teorema Trabajo-Energía” (o Principio Trabajo-Energía). Es la conexión que estábamos buscando entre la dinámica (las fuerzas a partir de las cuales calculamos el trabajo) y la cinemática (el cambio en la energía cinética). A diferencia de la Segunda Ley de Newton, que relaciona dos cantidades vectoriales (la suma vectorial de las fuerzas y el vector de aceleración), el Teorema de Trabajo-Energía relaciona dos cantidades escalares entre sí (trabajo y energía cinética). Aunque introdujimos la energía cinética como una forma de calcular la integral para el trabajo neto, si se conoce el valor del trabajo neto realizado en un objeto, entonces se puede utilizar el Teorema de Trabajo-Energía para calcular el cambio en la velocidad del objeto.

Lo más importante es que el teorema Trabajo-Energía introduce el concepto de “energía”. Como veremos en capítulos posteriores, existen otras formas de energía además del trabajo y la energía cinética. El Teorema Trabajo-Energía es el punto de partida para la idea de que se puede convertir una forma de energía en otra. El Teorema Trabajo-Energía nos dice cómo una fuerza, al hacer el trabajo, puede proporcionar energía cinética a un objeto o eliminar energía cinética de un objeto.

Ejemplo\(\PageIndex{1}\)

\(W\)Se realizó un trabajo neto de sobre un objeto de masa\(m\) que comenzó en reposo. ¿Cuál es la velocidad del objeto después de que se haya realizado el trabajo en el objeto?

Solución:

Usando el Teorema de Trabajo y Energía:

\ begin {alinear*} W =\ frac {1} {2} mv_f^2 -\ frac {1} {2} mv_i^2\ end {align*}

donde\(v_i\) está la velocidad inicial del objeto y\(v_f\) es su velocidad final. Dado que la velocidad inicial es cero, podemos encontrar fácilmente la velocidad final:

\ begin {align*} v_f =\ sqrt {\ frac {2W} {m}}\ end {alinear*}

Ejemplo\(\PageIndex{2}\)

Se presiona un bloque contra el extremo libre de un resorte horizontal con constante de resorte\(k\), para comprimir el resorte por una distancia\(D\) relativa a su longitud de reposo, como se muestra en la Figura\(\PageIndex{2}\). El otro extremo del muelle está fijado a una pared.

Figura\(\PageIndex{2}\): Un bloque se presiona contra un resorte horizontal para comprimir el resorte una distancia\(D\) relative to its rest length.

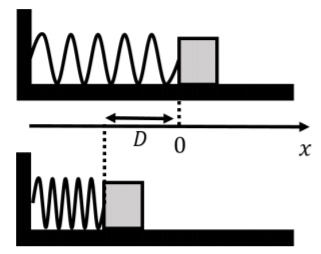
Si el bloque se libera del reposo y no hay fricción entre el bloque y la superficie horizontal, ¿cuál es la velocidad del bloque cuando sale del muelle?

Solución:

Este es el mismo problema que presentamos en el Capítulo 6 del Ejemplo 6.2.2, donde resolvimos una ecuación diferencial para encontrar la velocidad.

Nuestro primer paso es calcular el trabajo neto realizado sobre el objeto al pasar de\(x=-D\) a\(x=0\) (que corresponde a cuando el objeto sale del resorte, como se discute en el Ejemplo 6.2.2). Las fuerzas sobre el objeto son:

1. \(\vec F_g\), su peso, con magnitud\(mg\).
2. \(\vec N\), la fuerza normal ejercida por el suelo.
3. \(\vec F(x)\), la fuerza del resorte, con magnitud\(kx\).

Tanto la fuerza normal como el peso son perpendiculares al desplazamiento, por lo que no harán ningún trabajo. El trabajo neto realizado es así el trabajo realizado por el resorte, que calculamos en el Ejemplo 7.1.1 como:

\ begin {align*} W^ {net} = W_F =\ frac {1} {2} kd^2\ end {align*}

Por el Teorema Trabajo-Energía, esto es igual al cambio en la energía cinética. Al señalar que el objeto comenzó en reposo (\(v_i=0\)),\(v_f\) se encuentra que la velocidad final es:

\ begin {align*} W^ {net} &=\ frac {1} {2} mv_f^2 -\ frac {1} {2} mv_i^2 =\ frac {1} {2} mv_f^2 - 0\\ frac {1} {2} kd^2 &=\ frac {1} {2} mv_f^2\\ vpor lo tanto _f &=\ sqrt {\ frac {kd^2} {m}}\ end {alinear*}

Ejemplo\(\PageIndex{3}\)

Se presiona un bloque contra el extremo libre de un resorte horizontal con constante de resorte\(k\), para comprimir el resorte por una distancia\(D\) relativa a su longitud de reposo, como se muestra en la Figura\(\PageIndex{3}\). El otro extremo del muelle está fijado a una pared.

Figura\(\PageIndex{3}\): Un bloque se presiona contra un resorte horizontal para comprimir el resorte una distancia\(D\) relativa a su longitud de reposo.

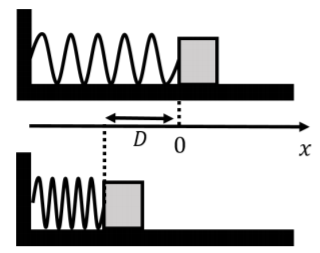
Si el bloque se libera del reposo y el coeficiente de fricción cinética entre el bloque y la superficie horizontal es\(\mu_k\), ¿cuál es la velocidad del bloque cuando sale del muelle?

Solución:

Este es el mismo ejemplo que el anterior, pero con fricción cinética. Las fuerzas en el bloque son:

1. \(\vec F_g\), su peso, con magnitud\(mg\).
2. \(\vec N\), la fuerza normal ejercida por el suelo sobre el bloque.
3. \(\vec F(x)\), la fuerza del resorte, con magnitud\(kx\).
4. \(\vec f_k\), la fuerza de fricción cinética, con magnitud\(\mu_kN\).

Tanto la fuerza normal como el peso son perpendiculares al desplazamiento, por lo que no harán ningún trabajo. Además, dado que la aceleración en dirección vertical es cero, la fuerza normal tendrá la misma magnitud que el peso (\(N=mg\)). La magnitud de la fuerza de fricción cinética es así\(f_k = \mu_k mg\). El trabajo neto realizado será la suma del trabajo realizado por el resorte\(W_F\), y el trabajo realizado por fricción,\(W_f\):

\ begin {align*} W^ {net} = W_F + W_F\ end {align*}

Ya hemos determinado el trabajo realizado por la primavera:

\ begin {align*} W_F =\ frac {1} {2} kd^2\ end {align*}

El trabajo realizado por la fuerza de fricción cinética será negativo (ya que está en la dirección opuesta al movimiento) y viene dado por:

\ begin {alinear*} w_f =\ vec f_k\ cdot\ vec d = -f_kd = -\ mu_kmgd\ end {align*}

Aplicando el teorema de la energía de trabajo, y señalando que el bloque comenzó en reposo (\(v_i=0\)),\(v_f\) se encuentra que la velocidad final es:

\ begin {align*} W^ {net} =W_F + W_f&=\ frac {1} {2} mv_f^2 -\ frac {1} {2} mv_i^2\\ frac {1} {2} kd^2-\ mu_kmgd &=\ frac {1} {2} mv_f^2\\ por lo tanto v_f &=\ sqrt {\ frac {kd^2} {m} -2\ mu_kgd}\ end {align*}

Discusión:

Podemos pensar en esto en términos del concepto de energía. El resorte realiza un trabajo positivo en el bloque, y así aumenta su energía cinética. La fricción hace trabajo negativo en el bloque, disminuyendo su energía cinética. Solo el resorte está “introduciendo” energía en el bloque, ya que la fricción está eliminando esa energía haciendo un trabajo negativo. Otra forma de pensarlo es que el resorte está ingresando energía; parte de esa energía se destina a aumentar la energía cinética del bloque, y parte de ella se pierde por la fricción. La energía que se pierde por fricción puede pensarse como “energía térmica” (calor) que sube al calentamiento del bloque y la superficie. En efecto, si te frotas la mano contra la mesa, notarás que se calienta; ¡estás perdiendo parte de la energía introducida en tu mano por el trabajo realizado por tu brazo para calentar la mesa y tu mano! Esto demuestra que podemos pensar en modelar la fricción usando energía térmica en lugar de una fuerza.