12.1: Energía cinética rotacional de un objeto

En esta sección, mostramos cómo definir la energía cinética rotacional de un objeto que está rotando alrededor de un eje estacionario en un marco de referencia inercial. Considera un objeto sólido que está rotando alrededor de un eje con velocidad angular,\(\vec\omega\), como se representa en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Un objeto que gira alrededor de un eje que es perpendicular a la página.

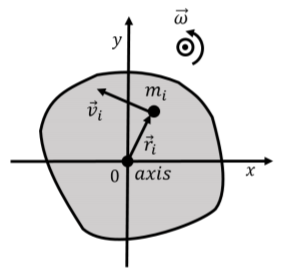
Podemos modelar el objeto como compuesto de muchas partículas puntuales, cada una con una masa\(m_i\), ubicada en una posición\(\vec r_i\), con velocidad\(\vec v_i\) relativa al eje de rotación. Elegimos un sistema de coordenadas cuyo origen está en el eje de rotación y cuyo\(z\) eje es colineal con el eje de rotación, como se representa en la Figura\(\PageIndex{1}\).

Cada partícula de masa\(m_i\) en el objeto tiene una energía cinética,\(K_i\):\[\begin{aligned} K_i = \frac{1}{2}m_iv_i^2\end{aligned}\] Podemos sumar la energía cinética de cada partícula juntos para obtener la energía cinética rotacional total\(K_{rot}\),, del objeto:\[\begin{aligned} K_{rot} = \sum_i \frac{1}{2}m_iv_i^2\end{aligned}\] Aunque cada partícula tendrá un diferente velocidad\(\vec v_i\),, todos tendrán la misma velocidad angular,\(\vec\omega\). Para cualquier partícula, ubicada a una\(r_i\) distancia del eje de rotación, su velocidad está relacionada con la velocidad angular del objeto por:\[\begin{aligned} \vec v_i &= \vec \omega \times \vec r_i\\ v_i &= \omega r_i\end{aligned}\] dónde\(\vec \omega\) y\(\vec r_i\) son siempre perpendiculares entre sí, ya que\(\vec\omega\) está fuera de el plano de la página. Además, el vector de velocidad\(\vec v_i\), siempre será perpendicular a\(\vec r_i\), ya que todas las partículas se mueven en círculos centrales alrededor del eje de rotación. Así podemos escribir la energía cinética rotacional total del objeto usando la velocidad angular:\[\begin{aligned} K_{rot} &= \sum_i \frac{1}{2}m_iv_i^2 = \sum_i \frac{1}{2}m_ir_i^2\omega^2= \frac{1}{2} \omega^2 \sum_i m_ir_i^2\\ &=\frac{1}{2}I\omega^2\end{aligned}\] donde factorizamos\(\omega\) y la mitad de la suma, ya que estas son las mismas para cada partícula\(i\). Luego reconocimos que la suma restante es simplemente la definición del momento de inercia del objeto alrededor del eje:\[\begin{aligned} I = \sum_i mr_i^2\end{aligned}\]

Así, la energía cinética rotacional de un objeto que gira con velocidad angular\(\omega\) alrededor de un eje que es estacionario en un marco inercial de referencia viene dada por:

\[K_{rot} = \frac{1}{2}I\omega ^{2}\]

donde\(I\) está el momento de inercia del objeto alrededor de ese eje. La energía cinética rotacional es funcionalmente muy similar a la energía cinética lineal; en lugar de la masa, usamos el momento de inercia, y en lugar de la velocidad al cuadrado, usamos la velocidad angular al cuadrado.

Trabajar sobre un objeto giratorio

Podemos calcular el trabajo realizado por una fuerza ejercida sobre un objeto que gira alrededor de un eje estacionario en un marco de referencia inercial. Dejar\(\vec F\) ser una fuerza ejercida en posición,\(\vec r\), relativa al eje de rotación en algún instante en el tiempo, y dejar que la fuerza se ejerza en el plano perpendicular al eje de rotación, como se ilustra en la Figura\(\PageIndex{2}\). Debido a que el objeto está girando alrededor del eje dado, solo la componente de la fuerza que es tangente al círculo alrededor del cual el punto donde se ejerce la fuerza puede hacer trabajo (solo la componente de la fuerza que es paralela al desplazamiento puede hacer trabajo).

El trabajo realizado por la fuerza a medida que el objeto gira un cierto ángulo viene dado por:\[\begin{aligned} W = \int \vec F \cdot d\vec l = \int F_\perp dl\end{aligned}\] donde\(d\vec l\) se encuentra un pequeño desplazamiento a lo largo de la trayectoria (circular) seguido por el punto donde se ejerce la fuerza, como se ilustra en la Figura\(\PageIndex{2}\). \(F_\perp\)es el componente de\(\vec F\) que es perpendicular al vector,\(\vec r\), desde el eje de rotación hasta la ubicación donde se ejerce la fuerza (\(F_\perp\)es el componente de\(\vec F\) que es tangente al círculo).

Figura\(\PageIndex{2}\): Calcular el trabajo realizado por una fuerza sobre un objeto giratorio.

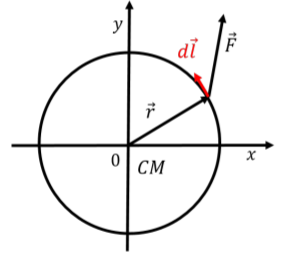
En algún instante en el tiempo, cuando la fuerza se ejerce en la posición\(\vec r\),, considerar el producto escalar entre el par de la fuerza\(\vec \tau\), y un desplazamiento angular infinitesimal,\(d\vec \theta\), alrededor del eje de rotación:\[\begin{aligned} \vec\tau \cdot d\vec\theta = (\vec r \times \vec F) \cdot \left(\frac{1}{r^2} \vec r\times d\vec l\right)\end{aligned}\] Los vectores \(\vec \tau\)y\(d\vec \theta\) son paralelos al eje de rotación (porque\(\vec F\) y\(d\vec l\) están en el plano perpendicular al eje de rotación), por lo que su producto escalar será igual al producto de sus magnitudes. El vector\(\vec r \times \vec F\) tiene una magnitud de:\[\begin{aligned} \vec r \times \vec F = rF_\perp\end{aligned}\] donde\(F_\perp\) está el componente de la fuerza tangente al círculo. El vector\(\vec r\times d\vec l\) tiene una magnitud:\[\begin{aligned} \vec r\times d\vec l = rdl\end{aligned}\] ya\(\vec r\) y\(d\vec l\) son siempre perpendiculares. El producto escalar\(\vec\tau \cdot d\vec\theta\) es así igual a:\[\begin{aligned} \vec\tau \cdot d\vec\theta = rF_\perp \frac{1}{r^2} rdl = F_\perp dl\end{aligned}\] El trabajo realizado por una fuerza cuando un objeto gira alrededor de un eje puede escribirse así en términos de su par alrededor de ese eje y el desplazamiento angular correspondiente de\(\theta_1\) a\(\theta_2\):

\[W=\int_{\theta _{1}}^{\theta _{2}}\vec\tau\cdot f\vec\theta \]

El trabajo neto realizado en un objeto a través de un desplazamiento angular de\(\theta_1\) a\(\theta_2\) puede escribirse así usando el par neto\(\vec \tau^{net}\) ejercido sobre el objeto:\[\begin{aligned} W^{net} = \int_{\theta_1}^{\theta_2}\vec\tau^{net}\cdot d\vec \theta\end{aligned}\] Podemos reorganizar esto usando la Segunda Ley de Newton para la dinámica rotacional:\[\begin{aligned} \vec\tau^{net} &= I \vec\alpha\\ &= I \frac{d\vec\omega}{dt} = I \frac{d\omega}{d\theta}\frac{d\vec\theta}{dt}=I \frac{d\omega}{d\theta} \vec\omega\end{aligned}\] que nos permite escribir la integral sobre un cambio en la velocidad angular en lugar de desplazamiento angular:\[\begin{aligned} W^{net} &= \int_{\theta_1}^{\theta_2}\vec\tau^{net}\cdot d\vec \theta = \int_{\theta_1}^{\theta_2}I \frac{d\omega}{d\theta} \vec\omega \cdot d\vec \theta\\ &=\int_{\omega_1}^{\omega_2}I \omega d\omega = \frac{1}{2}I\omega_2^2 - \frac{1}{2}I\omega_1^2\end{aligned}\] donde se utilizó el hecho de que\(\vec\omega\)\(d\vec\theta\) son paralelos. Por lo tanto, encontramos que el Teorema de Trabajo-Energía también se puede aplicar para encontrar el cambio en la energía cinética rotacional resultante del trabajo neto realizado por un par:

\[W^{net} = \int_{\theta _{1}}^{\theta _{2}}\vec\tau ^{net}\cdot d\vec\theta = \Delta K_{rot}\]

Si se ejerce un par constante\(\vec\tau\),, sobre un objeto que está rotando a velocidad angular constante\(\vec\omega\), entonces la velocidad a la que se está realizando ese trabajo viene dada por:\[\begin{aligned} P = \frac{dW}{dt} = \frac{d}{dt} \vec \tau \cdot d\vec\theta = \vec \tau \cdot \frac{d\vec\theta}{dt} = \vec \tau \cdot \vec\omega\end{aligned}\] Esto es muy similar a la potencia,\(P=\vec F\cdot \vec v\), con la que una fuerza sí funciona en un objeto moviéndose con velocidad constante, excepto que en lugar de fuerza usamos torque, y en lugar de velocidad, usamos velocidad angular.

Energía cinética total de un objeto

En el marco de referencia del centro de masa, un objeto que gira alrededor de un eje a través de su centro de masa con velocidad angular\(\vec \omega\),, tendrá energía cinética rotacional\(K_{rot}\), dada por:\[\begin{aligned} K_{rot}=\frac{1}{2}I_{CM}\omega^2\end{aligned}\] dónde\(I_{CM}\) está el momento de inercia del objeto alrededor del eje a través de su centro de masa.

Deseamos determinar la energía cinética del objeto en un marco de referencia inercial donde el centro de masa del objeto se mueve con una velocidad\(\vec v_{cm}\); es decir, en un marco donde el eje de rotación se mueve con la velocidad del centro de masa. Modelamos el objeto como compuesto de partículas de masa\(m_i\), cada una ubicada en posición\(\vec r_i\), con relación al eje de rotación a través del centro de masa. La velocidad,\(\vec v_i\), de una partícula\(i\), en este marco de referencia, viene dada por:\[\begin{aligned} \vec v_i = \vec\omega \times \vec r_i + \vec v_{CM}\end{aligned}\] donde\(\vec\omega \times \vec r_i\) está la velocidad de la partícula como se ve en el centro de masa (debido a la rotación). La energía cinética de la partícula\(i\)\(K_i\),, viene dada por:\[\begin{aligned} K_i = \frac{1}{2}m_iv_i^2 = \frac{1}{2}m_i(\vec v_i\cdot \vec v_i)\end{aligned}\] donde expresamos la velocidad de la partícula al cuadrado usando un producto escalar de la velocidad de la partícula consigo misma. La energía cinética total del objeto se encuentra sumando las energías cinéticas de todas las partículas:\[\begin{aligned} K_{tot} &= \sum \frac{1}{2}m_i(\vec v_i\cdot \vec v_i) \\ &=\frac{1}{2} \sum_i m_i (\vec\omega \times \vec r_i + \vec v_{CM}) \cdot (\vec\omega \times \vec r_i + \vec v_{CM})\\ &=\frac{1}{2} \sum_i m_i (\vec\omega \times \vec r_i)\cdot(\vec\omega \times \vec r_i ) + \frac{1}{2} \sum_i m_i (\vec v_{CM}) \cdot (\vec v_{CM}) + \sum_i m_i (\vec\omega \times \vec r_i) \cdot (\vec v_{CM})\\ &=\frac{1}{2} \sum_i m_i \omega^2r_i^2 + \frac{1}{2} \sum_i m_i v_{CM}^2 + \sum_i m_i (\vec\omega \times \vec r_i) \cdot (\vec v_{CM})\\ &=\frac{1}{2} I_{CM}\omega ^2 + \frac{1}{2}M v_{CM}^2+\sum_i m_i (\vec\omega \times \vec r_i) \cdot (\vec v_{CM})\end{aligned}\] donde el primer término es la energía cinética rotacional que encontramos anteriormente. El segundo término, llamado la “energía cinética traslacional”, puede pensarse como la energía cinética de todo el sistema con masa\(M=\sum m_i\), debido al movimiento traslacional del centro de masa. El último término es idénticamente cero; podemos reordenar el producto escalar y\(\vec v_{CM}\) factorizar de la suma:\[\begin{aligned} \sum_i m_i (\vec\omega \times \vec r_i) \cdot (\vec v_{CM}) &= (\vec v_{CM}) \cdot \sum_i m_i (\vec\omega \times \vec r_i)\\ &=(\vec v_{CM}) \cdot \sum_i m_i \vec v'_{i}\end{aligned}\] donde\(v'_{i} = \vec\omega \times \vec r_i\) está la velocidad de la partícula\(i\) en el centro de masa marco de referencia. Pero la suma:\[\begin{aligned} \sum_i m_i \vec v'_{i}\end{aligned}\] es el numerador para la definición de la velocidad del centro de masa, que, en el centro de masa marco de referencia ¡es idéntico cero!

Así, la energía cinética total de un objeto de masa\(M\), que gira alrededor de un eje a través de su centro de masa con velocidad angular\(\omega\), y cuyo centro de masa se mueve con velocidad,\(\vec v_{CM}\), viene dada por:

\[K_{tot}=K_{rot}+K_{trans}=\frac{1}{2}I_{CM}\omega ^{2}+\frac{1}{2}Mv^{2}_{CM}\]

La energía cinética total se puede considerar como la suma de las energías rotacional y cinética.