12.2: Movimiento rodante

En esta sección, examinamos cómo modelar el movimiento de un objeto que está rodando a lo largo de una superficie, como el movimiento de una rueda de bicicleta. Considerar el movimiento de una rueda de radio,\(R\), girando con velocidad angular,\(\vec\omega\), alrededor de un eje perpendicular a la rueda y a través de su centro de masa, como se observa en el marco del centro de masa. Esto se ilustra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Una rueda que gira con velocidad angular\(\vec\omega\) alrededor de un eje a través de su centro de masa.

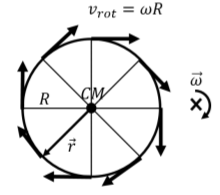
En el marco de referencia del centro de masa, cada punto en el borde de la rueda tiene una velocidad,\(\vec v_{rot}\), debido a la rotación dada por:\[\begin{aligned} \vec v_{rot} = \vec \omega\times \vec r \end{aligned}\] donde\(\vec r\) es un vector (de magnitud\(R\)) desde el centro de masa hasta el punto correspondiente en el borde de la rueda (mostrada en la Figura\(\PageIndex{1}\) para un punto en la parte inferior izquierda de la rueda). El vector siempre\(\vec r\) es perpendicular a\(\vec \omega\), de manera que la velocidad de todos los puntos en el borde, medida en el marco de referencia del centro de masa, es la misma:

\[v_{rot} = \omega R\]

como se ilustra en la Figura\(\PageIndex{1}\).

Ahora, supongamos que toda la rueda se mueve, ya que rueda sobre el suelo, de tal manera que el centro de masa de la rueda se mueve con una velocidad,\(\vec v_{CM}\), como se ilustra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Una rueda rodando sin deslizarse sobre el suelo, con el centro de masa moviéndose con velocidad\(\vec v_{CM}\). La rueda se muestra en diferentes instantes en el tiempo, ya que el punto mostrado en rojo se mueve alrededor del centro de masa.

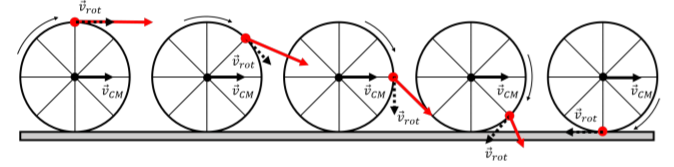
En el marco de referencia del suelo, cada punto en el borde de la rueda tendrá una velocidad\(\vec v\) dada por: Es\[\begin{aligned} \vec v = \vec v_{rot} + \vec v_{CM}\end{aligned}\] decir, en el marco de referencia del suelo, cada punto tendrá una velocidad obtenida (vectorialmente) sumando su velocidad relativa al centro de masa, \(\vec v_{rot}\), y la velocidad del centro de masa en relación con el suelo,\(\vec v_{CM}\). Esto se ilustra en la Figura\(\PageIndex{2}\) para un punto específico, mostrado en rojo. El vector rojo corresponde a la velocidad del punto rojo a medida que gira la rueda, y se obtiene sumando la velocidad del centro de masa\(\vec v_{CM}\), y la velocidad\(\vec v_{rot}\),, relativa al centro de masa (mostrado como el vector discontinua, tangente al borde de la rueda).

Considera, específicamente, el instante en el tiempo cuando el punto rojo está en la parte inferior de la rueda, donde la rueda hace contacto con el suelo. Si la rueda no se desliza con respecto al suelo, entonces el punto está, en ese instante, en reposo relativo al suelo. A este tipo de movimiento le llamamos “rodar sin resbalar”; el punto sobre el objeto giratorio que está en contacto con el suelo se encuentra instantáneamente en reposo con relación al suelo. Este es el escenario ilustrado en la Figura\(\PageIndex{2}\).

Para el punto en contacto con el suelo, los vectores\(\vec v_{rot}\) y\(\vec v_{CM}\) son antiparalelos, horizontales, y deben sumarse a cero. Escribiendo el componente horizontal de la velocidad de ese punto (eligiendo la dirección positiva para estar en la dirección de la velocidad del centro de masa):\[\begin{aligned} v &= -v_{rot} + v_{CM} = 0\\ \therefore v_{rot} &= v_{CM}\end{aligned}\] y encontramos que, para rodar sin resbalar, la velocidad debida a la rotación alrededor del centro de masa tiene que ser igual a la velocidad del centro de masa. La velocidad debida a la rotación alrededor del centro de masa se puede expresar usando la velocidad angular de la rueda alrededor del centro de masa (Ecuación 12.2.1). Para rodar sin resbalar, tenemos así la siguiente relación entre la velocidad angular y la velocidad del centro de masa:

\[\omega R=v_{CM}\qquad\text{(rolling without slipping)}\]

Tiene sentido que la velocidad angular esté relacionada con la velocidad del centro de masa. Cuanto más rápido gire la rueda, más rápido se moverá el centro de masa. Si la rueda se desliza con respecto al suelo, entonces el punto de contacto ya no es estacionario con relación al suelo, y no hay relación entre la velocidad angular y la velocidad del centro de masa. Para rodar con resbalones, imagina el movimiento de la rueda de tu bicicleta mientras intentas montar tu bicicleta sobre una capa de hielo resbaladiza.

Para rodar sin resbalar, la magnitud de la aceleración lineal del centro de masa,\(a_{CM}\), se relaciona de manera similar con la magnitud de la aceleración angular de la rueda,\(\alpha\), alrededor del centro de masa:\[\begin{aligned} a_{CM} &= \frac{dv_{CM}}{dt} = \frac{d}{dt}\omega R = R \frac{d\omega}{dt}\\ \therefore a_{CM} &= R\alpha\end{aligned}\]

Ejercicio\(\PageIndex{1}\)

Para rodar sin resbalar (Figura\(\PageIndex{2}\)), la velocidad del punto en la rueda que está en contacto con el suelo es\(0\). ¿Cuál es la velocidad del punto en la parte superior de la rueda?

1. \(0\).
2. \(v_{CM}\).
3. \(2v_{CM}\).
4. Ninguna de las anteriores.

Contestar

Ejemplo\(\PageIndex{1}\)

Figura\(\PageIndex{3}\): Un disco rodando sin deslizarse por una inclinación.

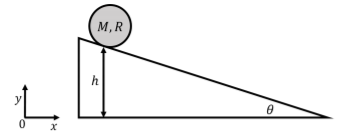
Solución:

Un disco de masa\(M\) y radio\(R\) se coloca sobre una pendiente a una altura\(h\) por encima del suelo. La inclinación hace un ángulo\(\theta\) con respecto a la horizontal, como se muestra en la Figura\(\PageIndex{3}\). Si el disco comienza en reposo y rueda sin deslizarse por la pendiente, ¿qué velocidad tendrá el centro de masa cuando el disco llegue al fondo de la inclinación? Podemos utilizar la conservación de la energía mecánica para determinar la velocidad del centro de masa en la parte inferior de la inclinación, ya que no hay fuerzas no conservadoras haciendo trabajo en el disco. Si elegimos definir la energía potencial gravitacional de tal manera que sea cero en la parte inferior de la pendiente, podemos escribir la energía mecánica total del disco en la parte superior de la pendiente como:\[\begin{aligned} E = K+U=(0)+Mgh\end{aligned}\] donde la energía cinética es cero, ya que el disco comienza en reposo ¹. En la parte inferior de la pendiente, el disco solo tendrá energía cinética, ya que la energía potencial en la parte inferior se define como cero. La energía cinética del disco tendrá un componente de la rotación del disco alrededor del centro de masa, con velocidad angular\(\omega\), y un componente de la traslación del centro de masa con velocidad\(v_{CM}\). La energía mecánica en la parte inferior de la inclinación es así:\[\begin{aligned} E' = K' + U = K'_{rot}+K'_{trans}+(0)=\frac{1}{2}I_{CM}\omega^2 + \frac{1}{2}Mv_{cm}^2\end{aligned}\] Dado que el disco está rodando sin deslizarse, su velocidad angular está relacionada con la velocidad del centro de masa:\[\begin{aligned} \omega = \frac{v_{CM}}{R}\end{aligned}\] El momento de inercia del disco alrededor de su centro de masa viene dado por:\[\begin{aligned} I_{CM}=\frac{1}{2}MR^2\end{aligned}\] Podemos escribir así lo mecánico energía en la parte inferior de la inclinación como:\[\begin{aligned} E' &= \frac{1}{2}I_{CM}\omega^2 + \frac{1}{2}Mv_{cm}^2\\ &=\frac{1}{2}\left( \frac{1}{2}MR^2 \right) \left( \frac{v_{CM}}{R}\right)^2+ \frac{1}{2}Mv_{cm}^2\\ &=\frac{3}{4}Mv_{cm}^2\end{aligned}\] Aplicar conservación de energía nos permite determinar la velocidad del centro de masa en la parte inferior de la inclinación:\[\begin{aligned} E &= E'\\ Mgh &= \frac{3}{4}Mv_{cm}^2\\ \therefore v_{CM} &= \sqrt{\frac{4}{3}gh}\end{aligned}\]

Discusión:

Este ejemplo mostró cómo podemos utilizar la conservación de energía para modelar el movimiento de un objeto que está rodando sin deslizarse. La restricción de rodar sin deslizamiento permitió que la velocidad angular del objeto se relacionara con la velocidad de su centro de masa.

Ejercicio\(\PageIndex{2}\)

Un aro, un disco y una esfera ruedan sin deslizarse por una inclinación. Si todos son liberados al mismo tiempo, ¿en qué orden llegarán al fondo?

1. Aro, disco, esfera.
2. Esfera, disco, aro.
3. Disco, esfera, aro.
4. Disco, aro, esfera.

Contestar

El eje de rotación instantáneo

Cuando un objeto está rodando sin deslizarse, podemos modelar su movimiento como la superposición de rotación alrededor del centro de masa y el movimiento de traslación del centro de masa, como en la sección anterior. Sin embargo, debido a que el punto de contacto entre el objeto rodante y el suelo es estacionario, también podemos modelar el movimiento como si el objeto estuviera girando instantáneamente con velocidad angular,\(\vec \omega\), alrededor de un eje estacionario a través del punto de contacto. Es decir, podemos modelar el movimiento solo como rotación, sin traslación, si elegimos un eje de rotación a través del punto de contacto entre el suelo y la rueda.

Llamamos al eje a través del punto de contacto el “eje de rotación instantáneo”, ya que, instantáneamente, aparece como si toda la rueda estuviera girando alrededor de ese punto. Esto se ilustra en la Figura\(\PageIndex{4}\), que muestra, en rojo, el vector de velocidad para cada punto en el borde de la rueda, en relación con el eje de rotación instantáneo. Debido a que el eje de rotación está fijado al suelo, la velocidad de cada punto alrededor de ese eje de rotación corresponde a la misma velocidad relativa al suelo que se representa en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{4}\): Una rueda que está rodando sin deslizarse, como se ve si gira alrededor del eje de rotación instantáneo que pasa por el punto de contacto con el suelo.

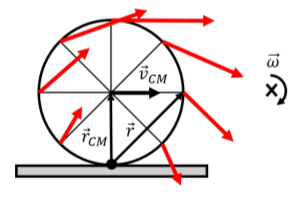
En particular, la velocidad angular\(\vec \omega\), alrededor del eje de rotación instantáneo es la misma que cuando modelamos el movimiento como traslación más rotación alrededor del centro de masa, como en la sección anterior. En efecto, en relación con el eje de rotación instantáneo, el centro de masa aún debe tener una velocidad\(\vec v_{CM}\), que viene dada por:\[\begin{aligned} \vec v_{CM} &= \vec\omega \times \vec r_{CM}\\ \therefore v_{CM} &= \omega R\end{aligned}\] dónde\(\vec r_{CM}\) está el vector desde el eje de rotación hasta el centro de masa. Esta es la misma condición para rodar sin resbalar que encontramos antes. De igual manera, la velocidad de cualquier punto de la rueda, relativa al suelo, viene dada por:\[\begin{aligned} \vec v = \vec\omega \times \vec r\end{aligned}\] donde\(\vec r\) está el vector desde el eje de rotación hasta el punto de interés (mostrado en la Figura\(\PageIndex{4}\) para el punto en el lado derecho de la rueda). En particular, el vector de velocidad (en rojo) para cualquier punto siempre es perpendicular al vector\(\vec r\) para ese punto, lo que no era necesariamente obvio al modelar el movimiento como rotación más traslación, como en la Figura\(\PageIndex{2}\).

Ejemplo\(\PageIndex{2}\)

Figura\(\PageIndex{5}\): Un disco rodando sin deslizarse por una inclinación.

Un disco de masa\(M\) y radio\(R\) se coloca sobre una pendiente a una altura\(h\) por encima del suelo. La inclinación hace un ángulo\(\theta\) con respecto a la horizontal, como se muestra en la Figura\(\PageIndex{5}\). ¿Cuál es la aceleración angular del disco, alrededor de un eje a través de su centro de masa, ya que rueda sin deslizarse por la pendiente?

Solución:

Para determinar la aceleración angular del disco alrededor del centro de masa, necesitamos modelar las fuerzas que se ejercen sobre el disco. Las fuerzas ejercidas sobre el disco son:

1. \(\vec F_g\), el peso del disco, ejercido hacia abajo en el centro de masa, con magnitud\(Mg\).
2. \(\vec N\), una fuerza normal perpendicular a la inclinación, ejercida por la inclinación en el punto de contacto con el disco.
3. \(\vec f_s\), una fuerza de fricción estática paralela a la inclinación, ejercida por la inclinación en el punto de contacto con el disco. Sin esta fuerza, el disco simplemente se deslizaría por la inclinación sin girar.

Estas fuerzas se ilustran en la Figura\(\PageIndex{6}\), junto con la aceleración del centro de masa, y nuestra elección del sistema de coordenadas (elegimos el\(x\) eje paralelo a la aceleración del centro de masa, para facilitar la aplicación de la Segunda Ley de Newton).

Figura\(\PageIndex{6}\): Las fuerzas sobre el disco rodando sin deslizarse por una inclinación.

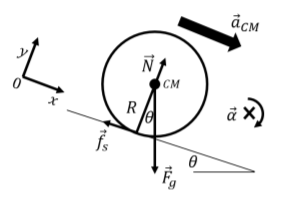
La aceleración angular del disco alrededor del centro de masa,\(\vec \alpha\) viene dada por la Segunda Ley de Newton para la dinámica rotacional:\[\begin{aligned} \vec\tau^{ext} = I_{CM}\vec\alpha\end{aligned}\] dónde\(\vec\tau^{ext}\) está el par externo neto en el disco alrededor del centro de masa (que estará en la\(z\) dirección negativa ).

La única fuerza que puede ejercer un par alrededor del centro de masa es la fuerza de fricción estática. La gravedad tiene un brazo de palanca de cero y la fuerza normal es antiparalela al vector que va desde el centro de masa hasta el punto donde se ejerce la fuerza. El par neto alrededor del centro de masa es así:\[\begin{aligned} \vec\tau^{ext} = \vec \tau_{f_s} = \vec r_{f_s}\times \vec f_s= -Rf_s\hat z\end{aligned}\] La aceleración angular será así en la\(z\) dirección negativa, y la magnitud viene dada por:\[\begin{aligned} \alpha = \frac{\tau^{ext}}{I_{CM}}=\frac{Rf_s}{\frac{1}{2}MR^2}=\frac{2f_s}{MR}\end{aligned}\] Sin embargo, desconocemos la magnitud de la fuerza de fricción estática. Podemos usar los\(y\) componentes\(x\) y de la Segunda Ley de Newton para determinarlo (con aceleración del centro de masa en la\(x\) dirección):\[\begin{aligned} \sum F_x &= F_g\sin\theta - f_s = Ma_{CM}\\ \sum F_y &= N - F_g\cos\theta = 0\end{aligned}\] Debido a que el disco está rodando sin deslizarse, la aceleración del centro de masa está relacionada con la aceleración angular del disco:\[\begin{aligned} a_{cm} = \alpha R\end{aligned}\] El\(x\) componente de la Segunda Ley de Newton puede así ser utilizado para determinar la magnitud de la fuerza de fricción estática en términos de la aceleración angular: Entonces\[\begin{aligned} Mg\sin\theta - f_s &= M \alpha R\\ \therefore f_s &= Mg\sin\theta - M\alpha R\end{aligned}\] podemos sustituir la fuerza de fricción de nuestra anterior fórmula para la aceleración angular:\[\begin{aligned} \alpha &= \frac{2f_s}{MR}\\ &=\frac{2Mg\sin\theta - 2M\alpha R}{MR} = \frac{2g\sin\theta}{R} - 2\alpha \\ \therefore \alpha &= \frac{2g\sin\theta}{3R}\end{aligned}\]

En lugar de modelar el movimiento del disco como rotación alrededor del centro de masa y traslación del centro de masa, también podemos modelarlo alrededor del eje de rotación instantáneo.

La aceleración angular alrededor del eje instantáneo de rotación será la misma que la aceleración angular alrededor del centro de masa. Acerca del eje de rotación instantáneo, solo la fuerza de gravedad puede ejercer un par, ya que la fuerza normal y la fuerza de fricción ambas tienen un brazo de palanca de cero. El par de torsión de la fuerza de gravedad, alrededor del eje de rotación instantáneo es:\[\begin{aligned} \vec \tau_g = -F_gR\sin\theta \hat z = -MgR\sin\theta \hat z \end{aligned}\] El par de la fuerza de gravedad es igual al momento de inercia del disco alrededor del eje de rotación instantáneo,\(I\), multiplicado por su aceleración angular:\[\begin{aligned} \tau ^{ext} = \tau_g &= I\alpha\\ \therefore \alpha &= \frac{\tau_g}{I} = \frac{MgR\sin\theta}{I}\end{aligned}\] El momento de la inercia sobre el eje instantáneo de rotación se encuentra fácilmente usando el teorema del eje paralelo:\[\begin{aligned} I = I_{CM}+MR^2 = \frac{1}{2}MR^2 + MR^2 =\frac{3}{2}MR^2\end{aligned}\] Esto nos permite encontrar la aceleración angular del disco:\[\begin{aligned} \alpha &= \frac{MgR\sin\theta}{I} = \frac{MgR\sin\theta}{\frac{3}{2}MR^2}\\ &=\frac{2g\sin\theta}{3R}\end{aligned}\] como encontramos anteriormente, pero en este caso, no necesitábamos usar la Segunda Ley de Newton para determinar la fuerza de fricción.

Discusión:

Vimos que podemos modelar la dinámica del cuerpo rodante usando un eje a través del centro de masa, o un eje a través del eje de rotación instantáneo. Esto último fue más fácil en este caso, porque no requería usar la Segunda Ley de Newton.

Al utilizar un eje a través del centro de masa para modelar el movimiento del disco, quedó claro que se requiere la fuerza de fricción estática para que el disco gire. Sin la fuerza de fricción estática, el disco se deslizaría a lo largo de la superficie de la inclinación. El disco aún podría girar si hay una fuerza de fricción cinética que provoque un par que haga girar el disco. Si la superficie fuera completamente sin fricción, el disco simplemente se deslizaría por la pendiente, y podríamos modelarlo como un bloque deslizante. Si la inclinación es demasiado pronunciada la fuerza de fricción estática ya no es suficiente para proporcionar el par necesario para que la aceleración angular sea la que corresponde a rodar sin deslizarse, y el disco se deslizaría.

Notas al pie

1. Técnicamente, la energía potencial debe tomarse para la altura del centro de masa, que es una\(h_{CM}=h+R\cos\theta\) distancia del suelo en la parte superior de la inclinación, y una altura\(h'_{CM}=R\) en la parte inferior de la inclinación. La diferencia neta de altura para el centro de masa es así\(h_{CM}-h'_{CM} = h+R(1-\cos\theta)\). Si asumimos que\(h\) es mucho más grande que\(R\), entonces esto es insignificante, de lo contrario, eso es lo que deberíamos usar en lugar de\(h\) para la energía potencial.