18.1: Energía Potencial Eléctrica

revisar temas

• Sección 8.1 sobre las fuerzas conservadoras.
• Sección 9.3 sobre la derivación de la energía potencial gravitacional.

Matemáticamente, la Ley de Coulomb para la fuerza eléctrica es idéntica a la Teoría Universal de la Gravedad de Newton para la fuerza gravitacional. La fuerza eléctrica es así conservadora, y el trabajo realizado por la fuerza eléctrica sobre una carga\(q\), cuando la carga se mueve de posición,\(A\), en el espacio a alguna otra posición,\(B\), no puede depender del camino tomado. Dado que el trabajo realizado por la fuerza eléctrica sólo depende de la ubicación de las posiciones inicial (\(A\)) y final (\(B\)), podemos definir una función de energía potencial eléctrico,\(U(\vec r)\), que depende de la posición,\(\vec r\). El trabajo realizado por la fuerza eléctrica\(\vec F^E\), sobre una carga al pasar de la posición,\(A\) (definida por el vector de posición,\(\vec r_A\)), a la posición,\(B\) (definida por el vector de posición,\(\vec r_B\)), puede escribirse como:

\[W=\int_A^B \vec F^{E}\cdot d\vec r=-\Delta U=-[U(\vec r_{B})-U(\vec r_{A})]\]

Para determinar la función,\(U(\vec r)\), podemos elegir una ruta sobre la cual la integral para el trabajo sea fácil de calcular. Considerar el trabajo realizado por la fuerza eléctrica desde una carga puntual,\(+Q\), ejercida sobre una carga,\(+q\), cuando\(+q\) se mueve de una distancia\(r_A\) a una\(r_B\) distancia del centro de\(+Q\), como se ilustra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Calcular el trabajo realizado sobre una carga\(+q\) por la fuerza eléctrica ejercida por la carga\(+Q\) cuando la carga\(+q\) se mueve de una distancia\(r_{A}\) a una\(r_{B}\) distancia del centro de carga\(+Q\).

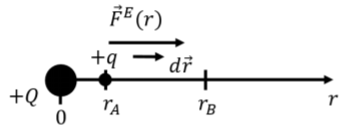
Colocando\(+Q\) en el origen de un sistema de coordenadas, la fuerza ejercida sobre la carga\(+q\),, cuando se ubica en posición\(\vec r\),, viene dada por:\[\begin{aligned} \vec F^E=k\frac{Qq}{r^2}\hat r\end{aligned}\] El trabajo realizado por la fuerza eléctrica cuando\(+q\) se mueve de\(A\) a \(B\)viene dado por:\[\begin{aligned} W&=\int_A^B \vec F^E\cdot d\vec r=\int_{\vec r_A}^{\vec r_B} \left(k\frac{Qq}{r^2}\hat r\right)\cdot d\vec r=kQq \int_{r_A}^{r_B} \frac{1}{r^2}dr\\ &=kQq \left[\frac{-1}{r} \right]_{r_A}^{r_B}=-\left(\frac{kQq}{r_B}-\frac{kQq}{r_A}\right)\end{aligned}\] donde señalamos que desde\(\vec F^E\) y\(d\vec r\) son paralelos, su producto escalar es simplemente el producto de sus magnitudes. Al comparar con la Ecuación 18.1.1, podemos identificar la energía potencial,\(U(\vec r)\), de una carga,\(+q\), ubicada en una posición relativa,\(\vec r\), a partir de una carga puntual,\(+Q\), como:

\[U(\vec r)=\frac{kQq}{r}+C\]

donde la energía potencial sólo se define hasta alguna constante\(C\), que se cancela cuando tomamos la diferencia de energía potencial entre dos posiciones. Obsérvese que esto es muy similar a la función para la energía potencial gravitacional de una masa\(m\),, una distancia\(r\),, de una masa,\(M\) (ver Sección 9.3).

La función de energía potencial que derivamos anteriormente sigue siendo la misma si una o ambas cargas cambian de signo, ya que la derivación no dependía del signo de las cargas,\(q\) y\(Q\), como cambiar el signo de una carga cambia la dirección de la fuerza. Por ejemplo, una carga positiva\(+q\), cerca de una carga negativa,\(-Q\), tendría energía potencial eléctrica negativa con la elección\(C=0\), en analogía exacta con la gravedad.

Energía potencial electrostática

Cuando mantenemos dos cargas positivas juntas a una distancia\(r\), aparte, necesitamos ejercer una fuerza sobre las cargas para mantener las cargas en su lugar (ya que se repelen entre sí). Si liberamos las cargas, se separarán entre sí, y eventualmente toda la energía potencial eléctrica almacenada se convierte en energía cinética. La energía que originalmente se almacenó en este “sistema” de dos cargas se denomina “energía potencial electrostática”. En esta sección, mostramos cómo modelar la energía almacenada en una colección de cargas puntuales.

Considera una sola carga positiva\(q_1\),, ubicada en el origen del espacio vacío. Ya que no hay otros cargos presentes, no nos “cuesta” ninguna energía colocar ese cargo ahí - no necesitamos hacer ningún trabajo. Si ahora traemos una segunda carga positiva,\(q_2\), y la colocamos a una distancia\(r_{12}\),, de\(q_1\) (Figura\(\PageIndex{2}\)), tendremos que hacer trabajo ya que\(q_1\) ejerce una fuerza sobre\(q_2\). Si definimos energía potencial cero\(C=0\) para estar en el infinito (elegir por energía eléctrica potencial), el trabajo\(W_{q2}\),, que debemos hacer\(q_2\) para traerlo del infinito a la distancia,\(r_{12}\), de\(q_1\) viene dado por el cambio correspondiente en energía potencial de\(q_2\):\[\begin{aligned} W_{q2}=\Delta U=U_{final}-U_{initial}=k\frac{q_1q_2}{r_{12}}-0=k\frac{q_1q_2}{r_{12}}\end{aligned}\] Tenga en cuenta que el trabajo lo hacemos nosotros (no por el campo eléctrico), por lo que tiene el mismo signo que el cambio en la energía potencial (debemos hacer un trabajo positivo para incrementar la energía potencial). El trabajo que realizamos corresponde a la misma cantidad de energía potencial electrostática almacenada en esta disposición de dos cargas (la única fuente de esa energía potencial electrostática almacenada es el trabajo que hicimos sobre la carga\(q_2\)).

Figura\(\PageIndex{2}\): Tres cargas positivas dispuestas juntas almacenarán cierta cantidad de energía potencial electrostática.

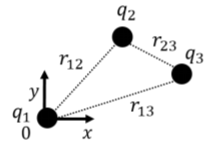
Ahora, traemos una tercera carga positiva\(q_3\), también desde infinitamente lejos, como se ilustra en la Figura\(\PageIndex{2}\). Para poder entrar\(q_3\), tenemos que hacer un trabajo contra las fuerzas ejercidas por ambos\(q_1\) y\(q_2\). Supongamos que colocamos\(q_3\) una\(r_{13}\) distancia de\(q_1\) y\(r_{23}\) de\(q_2\). Entonces, la cantidad de trabajo que realizamos para traer\(q_3\) viene dada por:\[\begin{aligned} W_{q3}=k\frac{q_1q_3}{r_{13}}+k\frac{q_2q_3}{r_{23}}\end{aligned}\] y la energía electrostática total almacenada en el sistema de tres cargas viene dada por la suma del trabajo realizado para colocar\(q_2\) y el trabajo realizado para colocar\(q_1\):\[\begin{aligned} E = W_{q1}+W_{q2}+W_{q3}=0+k\frac{q_1q_2}{r_{12}}+k\frac{q_1q_3}{r_{13}}+k\frac{q_2q_3}{r_{23}}\end{aligned}\] Si tenemos cualquier número de cargas (positivas y negativas), siempre podemos calcular la energía electrostática almacenada procediendo de manera similar.

Ejercicio\(\PageIndex{1}\)

Cuatro cargas de magnitud variable se fijan en posición. Si la energía potencial eléctrica almacenada en el sistema se calculara como se indicó anteriormente, ¿cuántos términos estarían en la suma?

1. Cuatro.
2. Dos.
3. Uno.
4. Seis.

Contestar