18.2: Potencial eléctrico

Como recuerda, definimos el campo eléctrico,\(\vec E(\vec r)\), para ser la fuerza eléctrica por unidad de carga. Al definir un campo eléctrico en todas partes del espacio, pudimos determinar fácilmente la fuerza en cualquier carga de prueba,\(q\), si la carga de prueba es positiva o negativa (ya que el signo de\(q\) cambiará la dirección del vector de fuerza,\(q\vec E\)): \[\begin{aligned} \vec E(\vec r) &= \frac{\vec F^E(\vec r)}{q}\\ \therefore \vec F^E(\vec r)&=q\vec E(\vec r)\end{aligned}\]De igual manera, definimos que el potencial eléctrico\(V(\vec r)\),, es la energía potencial eléctrica por unidad de carga. Esto nos permite definir el potencial eléctrico,\(V(\vec r)\), en todas partes del espacio, para luego determinar la energía potencial de una carga específica\(q\),, simplemente multiplicando\(q\) por el potencial eléctrico en esa posición en el espacio. \[\begin{aligned} V(\vec r) &= \frac{ U(\vec r)}{q}\\ \therefore U(\vec r)&= q V(\vec r)\end{aligned}\]La unidad S.I. para potencial eléctrico es el “voltio”, (V). El potencial eléctrico\(V(\vec r)\),, es un campo escalar cuyo valor es “el potencial eléctrico” en esa posición en el espacio. Una carga positiva,\(q=1\text{C}\), tendrá así una energía potencial de\(U=10\text{J}\) si se ubica en una posición en el espacio donde está el potencial eléctrico\(V=10\text{V}\), ya que\(U=qV\). De igual manera, una carga negativa\(q=-1\text{C}\),, tendrá energía potencial negativa,\(U=-10\text{J}\), en la misma ubicación.

Dado que solo las diferencias en la energía potencial son físicamente significativas (ya que el cambio en la energía potencial está relacionado con el trabajo), solo los cambios en el potencial eléctrico son físicamente significativos (ya que el potencial eléctrico está relacionado con la energía potencial eléctrica). Una diferencia en el potencial eléctrico se llama comúnmente “voltaje”. A menudo se hace una elección clara de dónde el potencial eléctrico es cero (típicamente la tierra, o infinitamente lejos), de modo que el término voltaje se usa para describir el potencial\(V\), en lugar de la diferencia de potencial,\(\Delta V\); esto solo se debe hacer cuando está claro dónde se encuentra se define la ubicación del potencial eléctrico cero.

Podemos describir una masa de caída libre al afirmar que la masa se mueve de una región donde tiene alta energía potencial gravitacional a una región de menor energía potencial gravitacional bajo la influencia de la fuerza de la gravedad (la fuerza asociada a una energía potencial siempre actúa en la dirección a las disminuciones energía potencial). Lo mismo ocurre con la energía potencial eléctrica: las cargas siempre experimentarán una fuerza en una dirección para disminuir su energía potencial eléctrica. Sin embargo, las cargas positivas experimentarán una fuerza que las conducirá de regiones de alto potencial eléctrico a regiones de bajo potencial eléctrico, mientras que las cargas negativas experimentarán una fuerza que las conducirá de regiones de bajo potencial eléctrico a regiones de mayor potencial eléctrico. Esto se debe a que, para cargas negativas, el cambio en la energía potencial asociada al movimiento por el espacio\(\Delta U\),, será el negativo del cambio correspondiente en el potencial eléctrico\(\Delta U=q\Delta V\), ya que la carga,\(q\), es negativa.

Ejercicio\(\PageIndex{1}\)

El potencial eléctrico aumenta a lo largo del\(x\) axis. A proton and an electron are placed at rest at the origin; in which direction do the charges move when released?

1. el protón se mueve hacia negativo\(x\), mientras que el electrón se mueve hacia positivo\(x\).
2. el protón se mueve hacia positivo\(x\), mientras que el electrón se mueve hacia negativo\(x\).
3. el protón y el electrón se mueven hacia negativo\(x\).
4. el protón y el electrón se mueven hacia positivo\(x\).

Contestar

Si la única fuerza ejercida sobre una partícula es la fuerza eléctrica, y la partícula se mueve en el espacio de tal manera que el potencial eléctrico cambia\(\Delta V\), podemos usar la conservación de energía para determinar el cambio correspondiente en la energía cinética de la partícula:

\[\begin{aligned} \Delta E&=\Delta U+\Delta K=0 \\ \Delta U&=q\Delta V \end{aligned}\]

\[\therefore \Delta K=-q\Delta V\]

donde\(\Delta E\) está el cambio en la energía mecánica total de la partícula, que es cero cuando se conserva la energía. La energía cinética de una partícula positiva aumenta si la partícula se mueve de una región de alto potencial a una región de bajo potencial (como\(\Delta V\) sería negativa y\(q\) es positiva), y viceversa para una partícula negativa. Esto tiene sentido, ya que una partícula positiva y negativa sienten fuerzas en direcciones opuestas.

Para describir las energías de partículas como los electrones, es conveniente utilizar una unidad de energía diferente a la del Joule, de manera que las cantidades involucradas no sean órdenes de magnitud menores a 1. Una elección común es el “electrón voltio”,. Un electrón voltio corresponde a la energía adquirida por una partícula con una carga de\(e\) (la carga del electrón) cuando es acelerada por una diferencia de potencial de\(1\text{V}\):\[\begin{aligned} \Delta E &= q\Delta V\\ 1\text{eV}&=(e)(1\text{V})=1.6\times 10^{-19}\text{J}\end{aligned}\] Un electrón que ha acelerado desde el reposo a través de una región con \(150\text{V}\)diferencia de potencial a través de ella tendrá una cinética de\(150\text{eV}=2.4\times 10^{-17}\text{J}\). Como puede ver, es más fácil describir la energía de un electrón en electrón voltios que Julios.

Ejercicio\(\PageIndex{2}\)

Una partícula se mueve desde un potencial eléctrico de\(-260\text{ V}\) to an electric potential of \(-600\text{ V}\) and loses kinetic energy. What is the charge of this particle?

1. Neutro.
2. Podría tener una carga positiva o negativa.
3. Positivo.
4. Negativo.

Contestar

Pensamientos de josh

A menudo es útil en física tomar conceptos previamente aprendidos y compararlos con otros nuevos, en este caso, la energía potencial gravitacional y la energía potencial eléctrica pueden compararse para ayudar a comprender el significado físico del potencial eléctrico.

Supongamos que un objeto con una gran masa,\(M\), está sentado en el espacio. Ahora coloca un objeto de una masa mucho menor,\(m\), a cualquier distancia,\(r\), desde el centro de\(M\). La energía potencial gravitacional de la pequeña masa viene dada por la siguiente fórmula:\[\begin{aligned} U_g&=\frac{GMm}{r}\end{aligned}\] Que es muy similar a la fórmula de la energía potencial eléctrica:\[\begin{aligned} U(\vec r)&=\frac{kQq}{r}\end{aligned}\] Ahora bien, si tuviéramos que sacar la masa\(m\) de su posición, ya no tendríamos un objeto con energía potencial gravitacional. Sin embargo, aún podríamos describir el potencial gravitacional para el punto\(r\), lo que resultaría en energía potencial gravitacional cuando\(m\) se coloca allí cualquier masa. Este es el equivalente gravitacional al potencial eléctrico, y puede definirse como:\[\begin{aligned} V_g&=\frac{U_g}{m}\end{aligned}\] que también es muy similar a la fórmula para el potencial eléctrico:\[\begin{aligned} V_E&=\frac{U_E}{q}\end{aligned}\] Esta comparación se ilustra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Energía potencial gravitacional y potencial gravitacional (izquierda) junto a su análogo eléctrico (derecha).

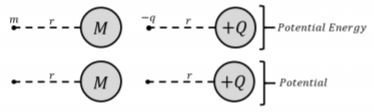
Ejemplo\(\PageIndex{1}\)

Un protón y un electrón se mueven desde una región del espacio donde el potencial eléctrico está\(20\text{V}\) to a region of space where the electric potential is \(10\text{V}\). If the electric force is the only force exerted on the particles, what can you say about their change in speed?

Solución:

Las dos partículas se mueven de una región del espacio donde está el potencial eléctrico\(20\text{V}\) a una región del espacio donde está el potencial eléctrico\(10\text{V}\). El cambio en el potencial eléctrico que experimentan las partículas es así:\[\begin{aligned} \Delta V = V_{final}-V_{initial}=(10\text{V})-(20\text{V})=-10\text{V}\end{aligned}\] y aprovechamos para enfatizar que se debe tener mucho cuidado con los signos al usar el potencial. El cambio en la energía potencial del protón, con carga\(q=+e\), es así:\[\begin{aligned} \Delta U_p=q\Delta V = (+e)(-10\text{V})=-10\text{eV}\end{aligned}\] La energía potencial del protón disminuye así en\(10\text{eV}\) (que se puede convertir fácilmente en julios). Ya que se nos dice que no se ejerce otra fuerza sobre la partícula, la energía mecánica total de la partícula (energías cinéticas más potenciales) debe ser constante. Así, si la energía potencial disminuyó, entonces la energía cinética del protón ha aumentado en la misma cantidad, y la velocidad del protón aumenta.

El cambio en la energía potencial del electrón, con carga\(q=-e\), es así:\[\begin{aligned} \Delta U_e=q\Delta V = (-e)(-10\text{V}) = 10\text{eV}\end{aligned}\] La energía potencial del electrón así aumenta en\(10\text{eV}\). Nuevamente, se conserva la energía mecánica del electrón, de manera que un aumento en la energía potencial da como resultado la misma disminución de la energía cinética y la velocidad del electrón disminuye.

Discusión:

Al usar el potencial eléctrico\(V\), modelamos el cambio en la energía potencial eléctrica de un protón y un electrón a medida que ambos se movían de una región del espacio a otra.

Se encontró que cuando un protón se mueve de una región de alto potencial eléctrico a una región de menor potencial eléctrico, su energía potencial disminuye. Esto se debe a que el protón tiene una carga positiva y una disminución en el potencial eléctrico también resultará en una disminución de la energía potencial. Dado que no se ejercen otras fuerzas sobre el protón, la energía cinética del protón debe aumentar. Debido a que la energía potencial del protón disminuye, el protón se mueve en la misma dirección que la fuerza eléctrica, y la fuerza eléctrica hace un trabajo positivo sobre el protón para aumentar su energía cinética.

Por el contrario, encontramos que cuando un electrón se mueve de una región de alto potencial eléctrico a una región de menor potencial eléctrico, su energía potencial aumenta. Esto se debe a que tiene una carga negativa y una disminución en el potencial eléctrico por lo tanto resulta en un aumento de la energía potencial. Como no se ejercen otras fuerzas sobre el electrón, la energía cinética del electrón debe disminuir, y el electrón se ralentiza. Esto tiene sentido, ya que la fuerza que se ejerce sobre un electrón estará en la dirección opuesta a la fuerza ejercida sobre un protón.

Potencial eléctrico del campo eléctrico

Al inicio de la Sección 18.1, determinamos la energía potencial de una carga puntual\(q\), en presencia de otra carga puntual,\(Q\) (Figura\(\PageIndex{1}\)). Esto se hizo calculando el trabajo realizado por la fuerza Coulomb (eléctrica) ejercida por carga\(Q\) sobre\(q\). Podemos escribir la misma integral para el trabajo realizado por la fuerza eléctrica sobre\(q\), pero utilizando el campo eléctrico,\(\vec E\), para escribir la fuerza:\[\begin{aligned} W&=\int_A^B \vec F^E\cdot d\vec r=\int_A^B q \vec E\cdot d\vec r=q \int_A^B \vec E\cdot d\vec r\end{aligned}\] donde reconocimos que la carga\(q\),, es constante y puede salir de la integral. La integral que queda es así el trabajo realizado por el campo eléctrico,\(\vec E\), por unidad de carga. En otras palabras, este es el cambio negativo en el potencial eléctrico:

\[\begin{aligned} W=q\int_{A}^{B}\vec E\cdot d\vec r=-q\Delta V=-q[V(\vec r_{B})-V(\vec r_{A})] \end{aligned}\]

\[\therefore\Delta V=V(\vec r_{B})-V(\vec r_{A})=-\int_A^B\vec E\cdot d\vec r\]

lo que nos permite determinar fácilmente el cambio en el potencial eléctrico asociado a un campo eléctrico. Tenga en cuenta que este resultado es general y no requiere que el campo eléctrico sea el de una carga puntual, y puede ser utilizado para determinar el potencial eléctrico asociado a cualquier campo eléctrico. También podemos especificar una función para el potencial, hasta una constante arbitraria,\(C\), (pensar integrales definidas versus indefinidas):\[\begin{aligned} V(\vec r)=-\int \vec E\cdot d\vec r + C\end{aligned}\] La relación entre el potencial eléctrico y el campo eléctrico es análoga a la relación entre la energía del potencial eléctrico y la fuerza eléctrica: \[\begin{aligned} \Delta V &=V(\vec r_B)-V(\vec r_A)=-\int_A^B \vec E\cdot d\vec r\\ \Delta U &=U(\vec r_B)-U(\vec r_A)=-\int_A^B \vec F^E\cdot d\vec r\end{aligned}\]ya que la ecuación inferior es solo\(q\) veces la primera ecuación. Podemos pensar en el potencial eléctrico siendo a la energía potencial lo que es el campo eléctrico a la fuerza eléctrica. El potencial eléctrico y el campo eléctrico son energía potencial eléctrico y fuerza eléctrica, por unidad de carga, respectivamente.

Para una carga puntual,\(Q\), ubicada en el origen, el campo eléctrico en alguna posición,\(\vec r\), viene dada por la Ley de Coulomb:\[\begin{aligned} \vec E=\frac{kQ}{r^2}\hat r\end{aligned}\] La diferencia potencial entre ubicación\(A\) (en posición\(\vec r_A\)) y ubicación\(B\) ( en posición\(\vec r_B\)), como en la Figura\(\PageIndex{1}\), viene dada por:\[\begin{aligned} \Delta V &=- \int_A^B \vec E\cdot d\vec r= -\int_{\vec r_A}^{\vec r_B} \frac{kQ}{r^2}\hat r\cdot d\vec r=-\left(\frac{kQ}{r_B}-\frac{kQ}{r_A}\right)\end{aligned}\] y observamos que podemos escribir una función para el potencial eléctrico,\(V(\vec r)\), a una\(r\) distancia de una carga puntual,\(Q\), como:\[\begin{aligned} V(\vec r)=\frac{kQ}{r}+C\end{aligned}\] donde \(C\)es una constante arbitraria. Esto, por supuesto, es idéntico al resultado que obtuvimos antes, para la energía potencial de una carga,\(q\), una distancia,\(r\), de\(Q\). \[\begin{aligned} U(\vec r)=qV(\vec r)=\frac{kQq}{r}+C'\end{aligned}\]donde la constante,\(C'=qC\), no tiene ningún impacto físico. A menudo, como es el caso de la gravedad, uno elige la constante\(C=0\). Esta elección corresponde a definir que la energía potencial sea cero en el infinito. Equivalentemente, esto corresponde a elegir el infinito para estar a un potencial eléctrico de\(0\text{V}\).

Ejercicio\(\PageIndex{3}\)

¿Qué causa que una partícula cargada positivamente gane velocidad cuando se acelera a través de una diferencia de potencial? :

1. La partícula se acelera porque pierde energía potencial a medida que se mueve de alto a bajo potencial.
2. La partícula se acelera porque pierde energía potencial a medida que se mueve de bajo a alto potencial
3. La partícula se acelera porque gana energía potencial.
4. La partícula acelera porque se mueve hacia cargas negativas.

Contestar

Ejemplo\(\PageIndex{2}\)

¿Cuál es el potencial eléctrico en el borde de un átomo de hidrógeno (una distancia de\(1\) from the proton), if one sets \(0\text{ V}\) at infinity? If an electron is located at a distance of \(1\) from the proton, how much energy is required to remove the electron; that is, how much energy is required to ionize the hydrogen atom?

Solución:

Podemos calcular fácilmente el potencial eléctrico, una distancia de\(1\unicode{xC5}\) desde un protón, ya que esto corresponde al potencial de una carga puntual (con\(C=0\)):\[\begin{aligned} V(\vec r)=\frac{kQ}{r}=\frac{(9\times 10^{9}\text{N}\cdot\text{m}^2\text{/C}^{2})(1.6\times 10^{-19}\text{C})}{(1\times 10^{-10}\text{m})}=14.4\text{V}\end{aligned}\] Podemos calcular la energía potencial del electrón (relativa al infinito, donde el potencial es \(0\text{ V}\), ya que elegimos\(C=0\)):\[\begin{aligned} U=(-e)V=(-1.6\times 10^{-19}\text{C})(14.4\text{V})=-14.4\text{eV}=-2.3\times 10^{-18}\text{J}\end{aligned}\] donde también expresamos la energía potencial en electrón-voltios. Para eliminar el electrón del átomo de hidrógeno, debemos ejercer una fuerza (hacer trabajo) hasta que el electrón esté infinitamente lejos del protón. Al infinito, la energía potencial del electrón será cero (por nuestra elección de\(C=0\)). Al mover el electrón del átomo de hidrógeno a una distancia infinita, debemos hacer un trabajo positivo para contrarrestar la fuerza atractiva del protón. El trabajo que debemos hacer es exactamente igual al cambio en la energía potencial del electrón (e igual al negativo del trabajo realizado por la fuerza ejercida por el protón):

\[\begin{aligned} W=\Delta U=(U_{final}-U_{initial})=(0\text{J}--2.3\times 10^{-18}\text{J})=2.3\times 10^{-18}\text{J} \end{aligned}\]

El trabajo positivo que debemos hacer, ejerciendo una fuerza que es opuesta a la fuerza eléctrica, es positivo e igual a\(2.3\times 10^{-18}\text{J}\), o\(14.4\text{eV}\). Si buscas la energía de ionización del hidrógeno, encontrarás que lo es\(13.6\text{eV}\), para que este modelo muy simplista sea bastante preciso (podríamos mejorar el modelo ajustando la distancia protón-electrón para que el potencial sea\(13.6\text{V}\)).

Discusión:

En este ejemplo, determinamos la energía potencial eléctrica de un electrón en un átomo de hidrógeno, y encontramos que es negativa, cuando la energía potencial se define como cero en el infinito. Para eliminar el electrón del átomo, debemos hacer un trabajo positivo con el fin de aumentar la energía potencial del electrón de un valor negativo a cero (la energía potencial en el infinito). Esto es análogo al trabajo que se debe realizar en un satélite en una órbita gravitacionalmente ligada para que alcance la velocidad de escape.

Ejemplo\(\PageIndex{3}\)

Dos grandes placas paralelas están separadas por una distancia,\(L\). The plates are oppositely charged and carry the same magnitude of charge per unit area, \(\sigma\). What is the potential difference between the two plates? Write an expression for the electric potential in the region between the two plates. Assume that the plates are large enough that you can treat them as infinite (that is, neglect what happens near the edges).

Solución:

La figura\(\PageIndex{2}\) muestra un diagrama de las dos placas paralelas con carga superficial sobre ellas.

Figura\(\PageIndex{2}\): Dos placas paralelas con densidades de carga superficial iguales y opuestas. En la región entre las placas, el campo eléctrico es uniforme.

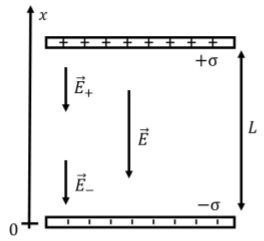
Sabemos por los capítulos anteriores que el campo eléctrico de la placa positiva no depende de la distancia de la placa y viene dado por:\[\begin{aligned} \vec E_+=-\frac{\sigma}{2\epsilon_0} \hat x\end{aligned}\] si aproximamos la placa como infinitamente grande. Esta es una aproximación razonable para la mayoría de los puntos excepto los que están cerca de los bordes de la placa, que ignoramos. El campo eléctrico de la placa negativa tendrá la misma magnitud y dirección, de tal manera que el campo eléctrico total,\(\vec E\), en todas partes entre las dos placas paralelas (siempre y cuando no estemos cerca de los bordes) viene dado por:\[\begin{aligned} \vec E=-\frac{\sigma}{\epsilon_0} \hat x\end{aligned}\] Tenga en cuenta que el campo eléctrico fuera de la región entre las dos placas es cero en todas partes, ya que el campo de las placas positivas y negativas apuntan en direcciones opuestas fuera de las placas y así cancelan (excepto cerca de los bordes de las placas). Por ejemplo, debajo de la placa negativa, el campo de la placa negativa apunta en la\(x\) dirección positiva (hacia la placa negativa), mientras que el campo desde la placa positiva apunta en la\(x\) dirección positiva (hacia la placa positiva).

Ahora podemos determinar la diferencia de potencial entre las dos placas, ya que conocemos el campo eléctrico en esa región. Usando el sistema de coordenadas que se muestra, calculamos la diferencia de potencial entre la placa positiva ubicada en\(x=L\) y la placa negativa ubicada en\(x=0\):\[\begin{aligned} \Delta V &=V(L)-V(0)=- \int_0^L \vec E\cdot d\vec x=-\int_0^L\frac{-\sigma}{\epsilon_0} \hat x \cdot d\vec x=\frac{\sigma}{\epsilon_0}\int_0^L dx=\frac{\sigma}{\epsilon_0}L\end{aligned}\] donde lo reconocimos\(\hat x\) y\(d\vec x\) son paralelas. Es muy fácil obtener la señal equivocada a la hora de calcular las diferencias potenciales, ¡así que ten cuidado!

Dado que la diferencia de potencial\(\Delta V=V(L)-V(0)\),, es positiva, la placa at\(x=L\) está a un potencial eléctrico más alto que la placa en\(x=0\). Esto tiene sentido, ya que una carga positiva en reposo se movería de la placa positiva a la placa negativa, disminuyendo así su energía potencial, lo que corresponde a pasar de una región de alto potencial eléctrico a una región de bajo potencial eléctrico. Por el contrario, una carga negativa en reposo se movería de la placa negativa a la placa positiva, disminuyendo su energía potencial, pero pasando de una región de bajo potencial eléctrico a una región de alto potencial eléctrico.

En general, si el campo eléctrico es constante, el cambio de potencial entre dos puntos separados por una distancia,\(L\), a lo largo de un eje que es antiparalelo con el campo (en este ejemplo, los puntos de campo en la\(x\) dirección negativa) viene dado por:\[\begin{aligned} \Delta V =- \int_0^L \vec E\cdot d\vec x=E\int_0^L dx= EL\end{aligned}\]

Tenga en cuenta que solo podemos calcular la diferencia en el potencial eléctrico entre las placas, no el valor real del potencial,\(V\). Si queremos definir un valor específico del potencial eléctrico, tenemos que elegir una ubicación donde definamos\(0\text{V}\) estar. Por convención, cuando sea posible, se elige la placa negativa para ser la ubicación de\(0\text{V}\). Para determinar el potencial eléctrico en cualquier lugar entre las dos placas, podemos calcular la diferencia de potencial entre la placa en\(x=0\) (la una en\(0\text{V}\)) y alguna posición entre las placas a lo largo del\(x\) eje (\(x<L\)): \[\begin{aligned} \Delta V &=V(x)-V(0)=-\int_0^x E \hat x \cdot d\vec x= Ex =\frac{\sigma}{\epsilon_0}x\\ \therefore V(x)&=V(0)+Ex=Ex=\frac{\sigma}{\epsilon_0}x\end{aligned}\]donde encontramos que el potencial eléctrico aumenta linealmente entre su valor en la placa negativa (\(0\text{V}\)) y su valor en la placa positiva (\(EL\)). Por supuesto, podríamos haber elegido cualquier valor del potencial eléctrico para la placa negativa, lo que equivale a elegir el valor de la constante arbitraria,\(C\).

En general, podemos escribir el potencial eléctrico en una región de campo eléctrico constante,\(\vec E=-E\hat x\), como:\[\begin{aligned} V(x)=Ex + C\end{aligned}\] Este escenario es muy similar a la fuerza gravitacional cerca de la superficie de la Tierra, donde el campo gravitacional es (casi) constante. Si eliges definir energía potencial gravitacional cero en la superficie de la Tierra, entonces, a medida que te mueves hacia arriba una\(h\) distancia del suelo, tu energía potencial gravitacional aumenta linealmente con\(h\) (\(U(h)=mgh\)). En nuestro caso, definimos energía potencial eléctrico cero para corresponder a la ubicación de la placa negativa (la placa negativa es así como la superficie de la Tierra, con un campo eléctrico constante apuntando hacia ella). A medida que una carga positiva se\(h\) aleja una distancia de la placa negativa, gana energía potencial eléctrica\(U(h)=qV(h)=qEh\), linealmente con la distancia de la placa. Si liberamos esa carga positiva, “caerá” de nuevo sobre la placa negativa. La principal diferencia con la gravedad, es que también podemos tener cargas negativas, que bajo gravedad, serían similares a las “masas negativas” (no es una cosa), que “caerían hacia arriba” (hacia la placa positiva).

Discusión:

En este ejemplo, examinamos el campo eléctrico entre dos placas paralelas con cargas opuestas sobre ellas, y vimos que el campo es constante y uniforme entre las placas y cero afuera (excepto por una pequeña región cerca del borde de las placas donde se descompone la suposición de placas infinitamente grandes). Se encontró que el potencial eléctrico disminuye linealmente en función de la distancia de una de las placas. Debido a que el campo eléctrico es constante entre las dos placas, la fuerza eléctrica sobre una carga puede tratarse de manera similar a la fuerza gravitacional sobre una masa cercana a la superficie de la Tierra. El potencial eléctrico resultante es lineal en la distancia de la placa negativa, así como\(mgh\) es lineal en\(h\), la distancia a la superficie de la Tierra. Las placas paralelas se utilizan a menudo para acelerar las cargas, por lo que son útiles de entender.

Ejercicio\(\PageIndex{4}\)

Si definimos un potencial gravicional,\(V(h)\), for particles a small distance, \(h\), from the surface of the Earth, it would have the form:

1. \(V(h) = mgh + C\).
2. \(V(h) = gh + C\).
3. \(V(h) = mg + C\).
4. \(V(h) = -mgh + C\).

Contestar

Campo eléctrico a partir del potencial eléctrico

revisar temas

• Sección 8.2 sobre determinar la fuerza a partir de la energía potencial.
• Sección A2.2 sobre gradientes.

En la sección anterior, encontramos que podríamos determinar el potencial eléctrico (un escalar) a partir del vector de campo eléctrico. En esta sección, mostramos cómo hacer la inversa, y determinar el vector de campo eléctrico a partir del potencial eléctrico. Consideremos, primero, un caso unidimensional, donde el campo eléctrico,\(\vec E(x)= E(x) \hat x\), apunta en la\(x\) dirección y depende de la posición,\(x\). En este caso unidimensional, el potencial eléctrico se obtiene de la anti-derivada negativa del campo eléctrico:\[\begin{aligned} V(x)=-\int \vec E(x)\cdot d\vec x=-\int E(x) dx\end{aligned}\] El campo eléctrico debe entonces ser dado por el negativo de la derivada de la función de potencial eléctrico:\[\begin{aligned} \vec E(x) = -\frac{dV(x)}{dx}\hat x\end{aligned}\] Tenga en cuenta que podemos decir de lo anterior que el campo eléctrico deben tener dimensiones de potencial eléctrico sobre la distancia. La unidad S.I. más común utilizada para describir el campo eléctrico es\(\text{V/m}\) (Voltios por metro).

Este resultado es muy similar al obtenido en la Sección 8.2, donde examinamos cómo se podría utilizar la energía potencial escalar,\(U(x,y,z)\), para determinar el vector de la fuerza asociada a esa energía potencial. Lo mismo ocurre con la fuerza eléctrica, donde podemos determinar el vector de fuerza eléctrica\(\vec F\), a partir de la energía potencial eléctrica, y de manera similar el campo eléctrico a partir del potencial eléctrico. En tres dimensiones, si conocemos la energía potencial eléctrica en función de la posición\(U(\vec r)=U(x,y,z)\), entonces el vector de fuerza eléctrica viene dado por:

\[\begin{aligned} \vec F(x,y,z) =- \nabla U=-\frac{\partial U}{\partial x}\hat x-\frac{\partial U}{\partial y}\hat y-\frac{\partial U}{\partial z}\hat z\end{aligned}\]

Del mismo modo, pero usando fuerza por unidad de carga (es decir, campo eléctrico) y energía potencial por unidad de carga (es decir, potencial eléctrico), encontramos:

\[\begin{aligned} \vec E(x,y,z) = -\nabla V =-\frac{\partial V}{\partial x}\hat x-\frac{\partial V}{\partial y}\hat y-\frac{\partial V}{\partial z}\hat z\end{aligned}\]

donde, como recordarás\(\nabla V\),, se llama el gradiente del campo escalar,\(V(x,y,z)\). El gradiente es un vector que apunta en la dirección del incremento máximo del valor de\(V(x,y,z)\). Para una carga positiva, esto corresponde a la dirección del incremento máximo de la energía potencial. Una carga positiva experimentará una fuerza en la dirección opuesta (en la dirección donde la energía potencial disminuye más rápidamente), y el campo eléctrico está así en la dirección opuesta al gradiente del potencial eléctrico.

Superficies equipotenciales

Podemos visualizar el potencial eléctrico de varias maneras, ya que es un campo escalar (tiene un único valor que puede diferir en todas partes en el espacio). La figura\(\PageIndex{3}\) muestra el potencial eléctrico cerca de una carga positiva\(+Q\), donde se ha optado por\(0\text{V}\) ubicarse en el infinito. El panel derecho muestra el potencial eléctrico como una “gráfica de superficie”, donde la dirección vertical es el valor del potencial eléctrico. El panel izquierdo muestra un “mapa de calor” del potencial eléctrico, donde el color corresponde al valor del potencial eléctrico.

Figura\(\PageIndex{3}\): Mapa de calor de potencial eléctrico (izquierda) y parcela de superficie (derecha) cerca de una sola carga positiva.

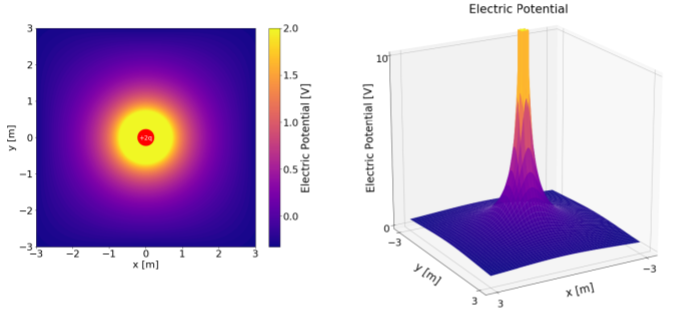
La forma más común de visualizar el potencial eléctrico es dibujar “curvas de nivel”, similar a cómo se dibujan curvas de nivel en un mapa geográfico. En un mapa geográfico, los contornos corresponden a líneas de altitud constante, que también son líneas de energía potencial gravitacional constante. De igual manera, podemos trazar líneas de potencial eléctrico constante para visualizar el potencial eléctrico. Las líneas de potencial constante se denominan “líneas equipotenciales”. En general, en tres dimensiones, las regiones de potencial eléctrico constante pueden ser superficies o volúmenes, llamadas “superficies/volúmenes equipotenciales”. En el Ejemplo 18.2.3 (con las placas paralelas) cada una de las placas forma una superficie equipotencial (por ejemplo, el potencial eléctrico se fijó en\(0\text{V}\) todas partes en la placa negativa).

Recordemos que, en algún momento del espacio, el vector de campo eléctrico siempre apunta en la dirección opuesta al gradiente del potencial eléctrico. A saber, el campo eléctrico apunta en la dirección en la que el potencial eléctrico disminuye más rápido. Esa dirección debe ser perpendicular a la dirección en la que el potencial eléctrico no cambia; es decir, el vector de campo eléctrico siempre es perpendicular a líneas/superficies equipotenciales. De manera más intuitiva, se puede pensar en una carga que se mueve a lo largo de un equipotencial. Por definición, la energía eléctrica potencial de la carga no cambia si se mueve a lo largo de un equipotencial. En consecuencia, la fuerza/campo eléctrico no puede hacer ningún trabajo sobre la carga, y por lo tanto debe ser perpendicular a la trayectoria de la carga (que elegimos para ser equipotencial).

Los materiales conductores son siempre superficies equipotenciales (o volúmenes) si las cargas no se mueven dentro del conductor. El campo eléctrico dentro de un conductor es siempre cero (en electrostática, cuando las cargas no se mueven), y así, una carga que se mueve a través de un conductor no experimenta fuerza eléctrica y su energía potencial eléctrica será constante; en otras palabras, todo el conductor es un equipotencial. De igual manera, debido a que el campo eléctrico siempre debe ser perpendicular a un equipotencial, las líneas de campo eléctrico siempre son perpendiculares a la superficie de un conductor (en electrostática).

Para dibujar líneas equipotenciales, se puede comenzar dibujando líneas de campo eléctrico, y luego dibujar líneas de contorno (cerradas) que están en todas partes perpendiculares a las líneas del campo eléctrico. Esto se ilustra en la Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\): El campo eléctrico y las líneas equipotenciales causadas por dos\(+2q\) cargas y una\(−3q\) carga (izquierda) y su correspondiente mapa de calor de potencial eléctrico (derecha).

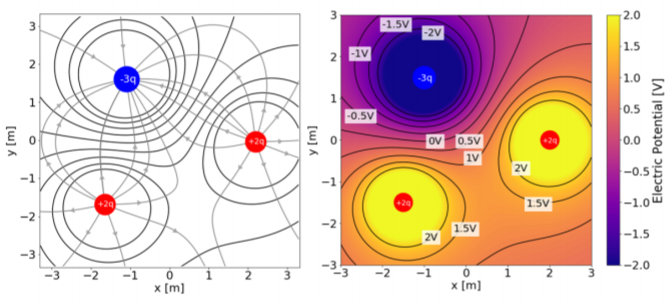
En general, es preferible dibujar líneas equipotenciales que estén separadas por incrementos iguales en el potencial eléctrico (así como en un mapa geográfico, las curvas de nivel corresponden a incrementos constantes de altitud). Esto requiere conocer una forma funcional para el potencial eléctrico. Por ejemplo, las líneas equipotenciales para una carga puntual ubicada en el origen consisten en círculos concéntricos centrados en el origen (en tres dimensiones, esto da como resultado superficies equipotenciales esféricas concéntricas). Si definimos\(0\text{V}\) estar en el infinito, el potencial eléctrico viene dado por:\[\begin{aligned} V(r)=\frac{kQ}{r}\end{aligned}\] Para dibujar líneas equipotenciales cada, digamos\(10\text{V}\),, los radios de los círculos equipotenciales correspondientes, para\(V=10\text{V}\)\(V=20\text{V}\),\(V=30\text{V}\), etc., están dadas por:\[\begin{aligned} r&=\frac{kQ}{V}\\ r_{10V}&=\frac{kQ}{(10\text{V})}\quad r_{20V}=\frac{kQ}{(20\text{V})}\quad r_{30V}=\frac{kQ}{(30\text{V})}\quad \dots\end{aligned}\]