18.8: Problemas y soluciones de la muestra
- Page ID
- 129391
Ejercicio\(\PageIndex{1}\)
Un cilindro largo de radio,\(R\), carries a uniform charge per unit volume density, \(\rho\). If the electric potential at the surface of the cylinder is \(V_S = 100\text{V}\), then what is the electric potential inside and outside of the cylinder as a function of \(r\), the distance from the center of the cylinder?
- Contestar
-
Para determinar el potencial eléctrico dentro y fuera del cilindro, podemos utilizar el campo eléctrico, que primero debemos determinar. Haremos esto usando la Ley de Gauss. Usaremos una superficie gaussiana que sea un cilindro de radio,\(r\), y longitud,\(L\). En ambas regiones, el flujo del campo eléctrico vendrá dado por:\[\begin{aligned} \int E dA = E 2\pi rL\end{aligned}\] ya que el campo eléctrico apunta en la dirección radial, lejos del centro del cilindro. Fuera del cilindro (\(r>R\)), la carga total encerrada es la carga total en una longitud,\(L\), del cilindro, que tiene un volumen,\(\pi R^2 L\):\[\begin{aligned} Q^{enc}=\rho \pi R^2 L\end{aligned}\] Así, aplicando la Ley de Gauss fuera del cilindro, da el campo eléctrico para\(r>R\) :\[\begin{aligned} \int E dA &= \frac{Q_{enc}}{\epsilon_0}\\ E 2\pi rL &= \frac{\rho \pi R^2 L}{\epsilon_0}\\ \therefore E(r) &= \frac{\rho R^2}{2\epsilon_0r}\quad(r\geq R)\end{aligned}\] Dentro del cilindro, la carga encerrada es aquella encerrada por un cilindro de radio,\(r\), y longitud,\(L\):\[\begin{aligned} Q^{enc}=\rho \pi r^2 L\end{aligned}\] Aplicando la Ley de Gauss, el campo eléctrico dentro del cilindro viene dado por:\[\begin{aligned} \int E dA &= \frac{Q_{enc}}{\epsilon_0}\\ E 2\pi rL &= \frac{\rho \pi r^2 L}{\epsilon_0}\\ \therefore E(r) &= \frac{\rho r}{2\epsilon_0}\quad(r<R)\end{aligned}\] Dado el campo eléctrico en todas partes en el espacio, nosotros ahora puede determinar el potencial eléctrico. Comenzaremos calculando el potencial eléctrico en cualquier parte del cilindro,\(V(r)\), utilizando la diferencia de potencial entre ese punto y la superficie del cilindro:\[\begin{aligned} \Delta V &= V_S - V(r) = -\int_{r}^{R} \vec E\cdot d \vec r\\ &= -\int_{r}^{R} \frac{\rho r}{2\epsilon_0} \hat r \cdot d \vec r\\ &= -\int_{r}^{R} \frac{\rho r}{2\epsilon_0} dr\\ &= -\frac{\rho (R^2-r^2)}{4\epsilon_0}\\ \therefore V(r) &= V_S + \frac{\rho (R^2-r^2)}{4\epsilon_0}\\ &=100\text{V}+\frac{\rho (R^2-r^2)}{4\epsilon_0}\end{aligned}\] Así, en todas partes dentro del cilindro, el potencial eléctrico es mayor que\(100\text{V}\), ya que \(R^2-r^2>0\). Esto tiene sentido, ya que el campo eléctrico apunta lejos del centro, y las cargas positivas disminuirán su energía potencial al alejarse más del centro.
Se procede de la misma manera para determinar la diferencia de potencial entre un punto a distancia,\(r>R\), y el potencial\(V_S\),, en la superficie del cilindro:\[\begin{aligned} \Delta V &= V(r) - V_S = -\int_{R}^{r} \vec E\cdot d \vec r\\ &= -\int_{R}^{r} \frac{\rho R^2}{2\epsilon_0r} \hat r \cdot d \vec r\\ &= - \frac{\rho R^2}{2\epsilon_0} \int_{R}^{r} \frac{1}{r}dr\\ &=- \frac{\rho R^2}{2\epsilon_0} \ln \left( \frac{R}{r} \right)\\ \therefore V(r) &= V_S - \frac{\rho R^2}{2\epsilon_0} \ln \left( \frac{R}{r} \right)\\ &= 100\text{V} - \frac{\rho R^2}{2\epsilon_0} \ln \left( \frac{R}{r} \right)\end{aligned}\] Encontramos que, fuera del cilindro, el potencial eléctrico disminuye desde\(100\text{V}\) como uno se aleja del cilindro, como se esperaba.
Ejercicio\(\PageIndex{2}\)
Un condensador se construye colocando una carcasa cilíndrica conductora concéntrica de espesor y radio interior despreciables\(R_B\), alrededor de un cilindro conductor sólido de radio\(R_A\), como se ilustra en la Figura\(\PageIndex{1}\). ¿Cuál es la capacitancia de este condensador, donde el cilindro sólido y la carcasa cilíndrica forman los dos electrodos?
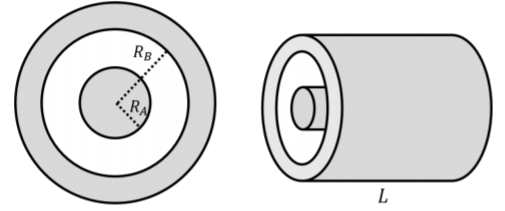
- Contestar
-
Determinaremos la capacitancia relacionando la diferencia de potencial entre los electrodos con la carga almacenada en los electrodos. Mediante el uso de la Ley de Gauss, podemos determinar el campo eléctrico entre los electrodos en función de la carga de esos electrodos, y a partir de ahí, podemos determinar la diferencia de potencial. Ignoraremos el hecho de que el cilindro tiene una longitud finita y que la Ley de Gauss no se mantendrá cerca de los bordes del cilindro, donde el campo eléctrico ya no está exactamente en la dirección radial.
Suponemos que cada electrodo lleva una carga igual y opuesta por unidad de longitud,\(\lambda\). Para determinar el campo eléctrico en la región\(R_A<r<R_B\), consideramos una superficie gaussiana que es un cilindro de radio,\(r\), y longitud\(L\), como se ilustra en la Figura\(\PageIndex{2}\), que encerrará una carga\(Q^{enc}=\lambda L\) desde el interior cilindro.
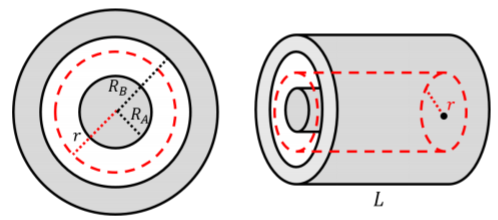
Figura\(\PageIndex{2}\): Resolver\(E\) entre dos cilindros usando la Ley de Gauss.
Aplicando la Ley de Gauss:\[\begin{aligned} \int E dA &= \frac{Q_{enc}}{\epsilon_0}\\ E 2\pi rL &= \frac{\lambda L}{\epsilon_0}\\ \therefore E(r) &= \frac{\lambda }{2\pi \epsilon_0 r}\end{aligned}\] y el campo eléctrico apunta en dirección radial (hacia afuera si el electrodo interno es positivo). Podemos encontrar la diferencia de potencial entre los dos electrodos usando el campo eléctrico:\[\begin{aligned} \Delta V &= V(R_B)-V(R_A)= -\int_{R_A}^{R_B} \vec E \cdot d\vec r\\ &=-\int_{R_A}^{R_B} \frac{\lambda }{2\pi \epsilon_0 r} dr\\ &= -\frac{\lambda }{2\pi \epsilon_0}\ln\left( \frac{R_B}{R_A} \right) \end{aligned}\] donde debemos señalar que el signo menos es ambiguo, ya que el signo real de la diferencia de potencial dependerá del signo de,\(\lambda\), la carga en el cilindro interior. Si la carga en el cilindro interior es positiva, la diferencia de potencial es negativa, lo que indica que el cilindro exterior está a un potencial menor que el interno (lo cual tiene sentido, ya que el campo eléctrico apuntaría hacia afuera entre los dos cilindros).
Podemos determinar la capacitancia entre los electrodos, tomando el valor absoluto de la diferencia de potencial anterior, y utilizando el hecho de que la carga\(Q\), en una longitud,\(L\), de un electrodo viene dada por\(Q=\lambda L\):\[\begin{aligned} Q &= C\Delta V\\ \lambda L &= C\frac{\lambda }{2\pi \epsilon_0}\ln\left( \frac{R_B}{R_A} \right)\\ \therefore C&=\frac{2\pi \epsilon_0}{L\ln\left( \frac{R_B}{R_A} \right)}\end{aligned}\] Observamos que la capacitancia no depende de la carga (arbitraria) por unidad de longitud,\(\lambda\) que colocamos en el cilindro interno para modelar el condensador. La capacitancia sólo depende de la geometría del condensador, y del material que se utilice entre las placas.


