19.2: Modelo microscópico de corriente
- Page ID
- 129066
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Considere un conductor cilíndrico de área de sección transversal\(A\), y longitud\(L\), como se muestra en la Figura\(\PageIndex{1}\). Una diferencia de potencial,\(\Delta V\), se aplica a través de la longitud del conductor, de manera que hay un campo eléctrico,\(\vec E\), en todas partes dentro del conductor. Si el conductor estuviera hecho de espacio vacío, los electrones entrarían en un extremo del conductor, acelerarían a través de la diferencia de potencial, y llegarían al otro extremo con una alta velocidad, habiendo ganado\(e\Delta V\) de energía cinética. En realidad, el conductor está hecho de materia, y los electrones no aceleran continuamente a través de toda la longitud del conductor. En cambio, solo pueden acelerar en una corta distancia antes de chocar con un átomo en el material (más bien, un electrón fuertemente unido en el material), y perder su energía cinética con el material, antes de acelerar de nuevo. El movimiento de los electrones que fluyen en un conductor se ilustra en la Figura\(\PageIndex{1}\) y muestra electrones moviéndose con un amplio rango de velocidades después de las colisiones, y solo un movimiento promedio en la dirección antiparalela al campo eléctrico.
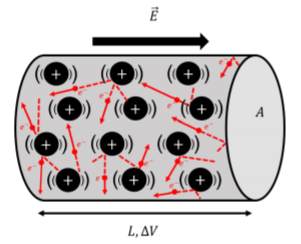
Así, cuando los electrones llegan al lado positivo del conductor, no han ganado ninguna energía cinética. En cambio, han perdido esa energía cinética a átomos del material conductor a través de colisiones; esos átomos luego vibran los cuales podemos medir como un aumento de la temperatura del material. Cuando la corriente fluye a través de un conductor, ese conductor se calentará; ¡así funcionan los elementos calefactores en tu tostadora!
Modelamos el movimiento de los electrones como cargas “a la deriva” a través del conductor con una velocidad\(\vec v_d\), la “velocidad de deriva”, como se ilustra en la Figura\(\PageIndex{2}\). En realidad, por supuesto, los electrones solo se mueven en promedio con la velocidad de deriva, y su velocidad instantánea es generalmente mucho mayor que la velocidad de deriva y puede ser en cualquier dirección, como se ilustra en la Figura\(\PageIndex{1}\).
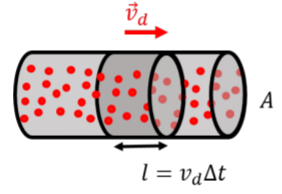
En un material conductor, cada átomo generalmente tendrá un electrón “libre” que está libremente unido y capaz de moverse fácilmente a través del material. El número de electrones libres disponibles para conducción por unidad de volumen\(n\),, dependerá de las propiedades del material (su densidad, cuántos electrones por átomo están disponibles, etc). Consideremos, entonces, el movimiento de los electrones de conducción presentes en una sección de longitud,\(l\), de un conductor, como se ilustra en la Figura\(\PageIndex{2}\). La cantidad de carga,\(\Delta Q\), contenida en una sección del conductor con longitud\(l\), viene dada por:\[\begin{aligned} \Delta Q= -e n Al\end{aligned}\] donde\(Al\) está el volumen de esa sección del conductor, y,\(e\), es la magnitud de la carga del electrón. El signo negativo es indicar que las cargas son negativas (son electrones). Esa carga tardará una cantidad de tiempo,\(\Delta t\), para fluir a través de un plano dado del conductor, de manera que podamos relacionar la longitud de la sección,\(l\), con la velocidad de deriva y\(\Delta t\):\[\begin{aligned} l&=v_d\Delta t\end{aligned}\] Así, la corriente que fluye a través de una sección transversal del conductor está dado por:
\[\begin{aligned} I =\frac{\Delta Q}{\delta t}=\frac{-enAl}{\Delta t}=-enAv_{d} \end{aligned}\]
\[\therefore I=-enAv_{d}\]
lo que nos permite conectar una cantidad macroscópica, corriente, a la descripción microscópica de cargas en movimiento. Tenga en cuenta que el signo negativo refleja el hecho de que la corriente (de cargas positivas) está en la dirección opuesta a la velocidad de deriva de los electrones (negativos). La densidad de corriente está directamente relacionada con las cantidades microscópicas, ya que no depende del área transversal (macroscópica)\(A\),, del conductor:
\[\begin{aligned} \vec j=\frac{I}{A}\hat E=-en\vec v_{d} \end{aligned}\]
\[\therefore \vec j=-en\vec v_{d}\]
donde, nuevamente, el signo negativo indica que la densidad de corriente está en la dirección opuesta a la velocidad de deriva real de los electrones, que a su vez es antiparalela al campo eléctrico.
Ejemplo\(\PageIndex{2}\)
Una corriente de\(1\text{A}\) is measured in a copper wire with a diameter of \(1\text{mm}\). What is the drift velocity of the electrons? Assume that each atom of copper provides one “free electron” for conduction.
Solución:
Para determinar la velocidad de deriva de los electrones, necesitamos conocer la densidad de electrones libres en el cobre. Para ello, necesitamos determinar cuántos átomos de cobre hay por unidad de volumen. La densidad del cobre es\(\rho=8.92\times 10^{3}\text{kg/m}^{3}\) y la unidad de masa atómica del cobre es\(63.5\text{amu}\) (\(1\text{mole}\)del cobre pesa\(63.5\text{g}\)). El número de átomos de cobre por unidad de volumen es así:
\[\begin{aligned} n=\frac{(6.022\times 10^{23}\text{mole}^{-1})(8.92\times 10^{3}\text{kg/m}^{3})}{(63.5\times 10^{-3}\text{kg/mole})}=8.46\times 10^{28}\text{m}^{-3}\end{aligned}\]
Dado que cada átomo de cobre aporta un electrón libre, esto es lo mismo que la densidad de los electrones libres. A partir de esto, obtenemos fácilmente la velocidad de deriva, a partir de la corriente:
\[\begin{aligned} v_d&=\frac{j}{en}=\frac{I}{Aen}=\frac{(1\text{A})}{\pi(0.0005\text{m})^2(1.6\times 10^{-19}\text{C})(8.46\times 10^{28}\text{m}^{-3})}\\ &=9.4\times 10^{-5}\text{m/s}\sim 0.1\text{mm/s}\end{aligned}\]
La velocidad de deriva es así muy lenta, inferior a un milímetro por segundo. Tenga en cuenta que un alambre de cobre de\(1\text{mm}\) diámetro en realidad no sería capaz de sostener una densidad de corriente tan alta sin daños.
Pensamientos de josh
Hay algunos tipos de velocidades que pueden confundirse fácilmente cuando se habla de la corriente: la velocidad de Fermi, la velocidad de deriva y la velocidad a la que se “completa” un circuito.
Comprender la velocidad Fermi requiere mecánica cuántica y está más allá del alcance de este libro de texto. Sin embargo, la velocidad de Fermi es representativa de la velocidad real de los electrones en un material conductor, principalmente debido a su energía térmica. En un buen conductor, estas velocidades son aproximadamente 1/200 la velocidad de la luz.
Si bien los electrones sí se mueven a su velocidad Fermi en un conductor, no se mueven en una trayectoria uniforme a través del conductor hacia el final del circuito. La mayor parte del movimiento de un electrón en un cable es caótico, pero en un circuito de CC, los electrones tienen una velocidad de deriva a través del conductor. Esta velocidad de deriva se define como la velocidad neta de los electrones en un conductor, y es causada por el campo eléctrico aplicado que tiene una pequeña cantidad de influencia en la dirección del movimiento del electrón que se mueve rápidamente. La velocidad de deriva de los electrones es muy lenta, teniendo a menudo una magnitud tan pequeña como decenas de micras por segundo.
Al comparar la velocidad de deriva con la velocidad de Fermi, imagínese parado dentro de un gran cilindro horizontal, que representará al conductor en esta analogía. El interior de este cilindro está forrado con cañones que disparan bolas de goma en todas las direcciones, que serán los electrones que se mueven a su velocidad Fermi. Ahora, imagina que estás intentando mover estas bolas de goma de alta velocidad de un extremo al otro del cilindro soplando un secador de pelo en esa dirección, que es el campo eléctrico que induce una velocidad de deriva.
Ahora que entendemos el caos cuántico que ocurre en un conductor, puede que estés pensando para ti mismo, “¿por qué la bombilla se enciende tan rápido después de que apelo el interruptor de la luz?”. Este es un pensamiento razonable, porque solo hemos cubierto el movimiento de partículas individuales en un conductor. Cuando un electrón se mueve muy ligeramente (a su velocidad de deriva), empujará a otros electrones en el conductor hacia adelante, provocando una reacción en cadena de electrones empujándose unos a otros hacia adelante. Este movimiento hace que los electrones fluyan a través del circuito, al igual que cómo fluye el agua a través de una tubería. La velocidad a la que se enciende una bombilla después del parpadeo de un interruptor es teóricamente la velocidad de la luz, pero los cortos retrasos causados por irregularidades en la forma en que los electrones chocan entre sí hacen que la velocidad sea aproximadamente del 50 al 99 por ciento de la velocidad de la luz.


