19.3: Ley de Ohm
- Page ID
- 129067
En la sección anterior, desarrollamos un modelo microscópico de cargas que se mueven en un conductor, pero no describimos cómo este movimiento se ve afectado por el campo eléctrico en el conductor (o equivalentemente, la diferencia de potencial a través del conductor). “Ley de Ohm” establece que la densidad de corriente\(\vec j\), en alguna posición en el conductor es proporcional al campo eléctrico,\(\vec E\), en esa misma posición en el conductor:
\[\begin{aligned} \vec j\propto \vec E \end{aligned}\]
\[\vec j=\sigma\vec E\]
donde hemos introducido la “conductividad”\(\sigma\), como la constante de proporcionalidad. La conductividad es una propiedad del material del que está hecho el conductor, y es una medida de cuán grande habrá una densidad de corriente (y por extensión, corriente) en el material dado un cierto campo eléctrico. Se dice que los materiales con una alta conductividad son buenos conductores, ya que una gran corriente resultará de un pequeño campo eléctrico. El oro y el cobre son ejemplos de materiales con una alta conductividad.
Ejercicio\(\PageIndex{1}\)
¿Cuál es la conductividad de un aislante ideal?
- \(0\).
- Más o menos\(1\).
- Infinito.
- Responder
-
Resistividad
Por conveniencia, a menudo se describe qué tan bien un material conduce cargas usando la “resistividad”\(\rho\), que simplemente se define como la inversa de la conductividad: Los\[\begin{aligned} \rho = \frac{1}{\sigma}\end{aligned}\] materiales con una alta resistividad son conductores pobres; tienden a “resistir” la formación de una corriente cuando una eléctrica campo se aplica. Los aislantes tienen alta resistividad.
Se ha observado que la resistividad de la mayoría (pero no de todos) los materiales aumenta linealmente con la temperatura del material. Se puede imaginar que, a medida que los átomos en el material vibran más, es más difícil que los electrones conduzcan a través del material ya que interactuarán con más átomos. La resistividad\(\rho\), a cierta temperatura\(T\), suele modelarse de la siguiente manera:\[\begin{aligned} \rho(T)=\rho_0\left[ 1 + \alpha (T-T_0)\right]\end{aligned}\] donde,\(\rho_0\), es una “resistividad de referencia” medida a una “temperatura de referencia”,\(T_0\) (generalmente\(\SI{20}{\degree C}\)). \(\alpha\)es el “coeficiente de temperatura” del material. La dependencia de la temperatura de la resistividad se ilustra en la Figura\(\PageIndex{1}\).
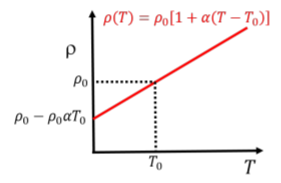
Este “modelo lineal” (ya que la resistividad aumenta linealmente con la temperatura) se encuentra empíricamente válido para muchos materiales en un amplio rango de temperaturas, aunque no se espera que se mantenga a temperaturas extremas (ya sea muy bajas o muy altas). Además, para los materiales semiconductores (como el silicio y el germanio), se encuentra que la resistividad disminuye en función de la temperatura.
Ejercicio\(\PageIndex{2}\)
¿Cuál es la pendiente de la resistividad vs temperatura como se muestra en la Figura\(\PageIndex{1}\)?
- \(\alpha\).
- \(\rho_0 \alpha T\).
- \(\rho_0 T\).
- \(\rho_0 \alpha\).
- Responder
El Cuadro 19.3.1 muestra una lista de materiales comunes y sus coeficientes de conductividad, resistividad y temperatura (definidos a una temperatura de referencia\(T_0=20^{\circ}\text{C}\)).
| Material | Resistividad\([\Omega\cdot m]\) | Coeficiente de temperatura\([^{\circ}\text{C}^{-1}]\) | Densidad de electrones libres\([\text{m}^{-3}]\) |
|---|---|---|---|
| Plata | \ ([\ Omega\ cdot m]\) ">\(1.59\times 10^{-8}\) | \ ([^ {\ circ}\ texto {C} ^ {-1}]\) ">\(0.0038\) | \ ([\ texto {m} ^ {-3}]\) ">\(5.86\times 10^{28}\) |
| Cobre | \ ([\ Omega\ cdot m]\) ">\(1.68\times 10^{-8}\) | \ ([^ {\ circ}\ texto {C} ^ {-1}]\) ">\(0.0040\) | \ ([\ texto {m} ^ {-3}]\) ">\(8.46\times 10^{28}\) |
| Oro | \ ([\ Omega\ cdot m]\) ">\(2.44\times 10^{-8}\) | \ ([^ {\ circ}\ texto {C} ^ {-1}]\) ">\(0.0034\) | \ ([\ texto {m} ^ {-3}]\) ">\(5.90\times 10^{28}\) |
| Aluminio | \ ([\ Omega\ cdot m]\) ">\(2.74\times 10^{-8}\) | \ ([^ {\ circ}\ texto {C} ^ {-1}]\) ">\(0.0039\) | \ ([\ texto {m} ^ {-3}]\) ">\(18.1\times 10^{28}\) |
| Hierro | \ ([\ Omega\ cdot m]\) ">\(9.70\times 10^{-8}\) | \ ([^ {\ circ}\ texto {C} ^ {-1}]\) ">\(0.0050\) | \ ([\ texto {m} ^ {-3}]\) ">\(17.0\times 10^{28}\) |
| Silicio | \ ([\ Omega\ cdot m]\) ">\(0.1-1000\) | \ ([^ {\ circ}\ texto {C} ^ {-1}]\) ">\(-0.0750\) | \ ([\ texto {m} ^ {-3}]\) ">\(0\) |
| Caucho | \ ([\ Omega\ cdot m]\) ">\((1-100)\times 10^{13}\) | \ ([^ {\ circ}\ texto {C} ^ {-1}]\) ">\(0\) | \ ([\ texto {m} ^ {-3}]\) ">\(0\) |
| Cuarzo | \ ([\ Omega\ cdot m]\) ">\(7.5\times 10^{17}\) | \ ([^ {\ circ}\ texto {C} ^ {-1}]\) ">\(0\) | \ ([\ texto {m} ^ {-3}]\) ">\(0\) |
Cuadro 19.3.1: Resistividad, densidad de electrones libres y coeficientes de temperatura de materiales comunes. Todas las propiedades están listadas para una temperatura de referencia de\(20^{\circ}\text{C}\).


