19.4: Resistencias
- Page ID
- 129035
Un conductor con corriente que lo atraviesa (o corriente que podría pasar por él) generalmente se llama “resistor”, para enfatizar que las cargas experimentarán resistencia a medida que viajan a través del conductor (ya que chocan con átomos en la resistencia). En esta sección, describimos las resistencias, cómo combinarlas y cómo modelar el calor que se genera cuando las cargas chocan con los átomos en la resistencia.
Resistencia
Considere una resistencia, con longitud\(L\), y área de sección transversal\(A\),, hecha de un material con resistividad\(\rho\), como se ilustra en la Figura\(\PageIndex{1}\).
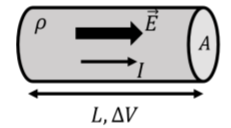
Una diferencia de potencial,\(\Delta V\), se aplica a lo largo de la longitud de la resistencia, dando como resultado un campo eléctrico,\(\vec E\), dentro de su volumen. A una buena aproximación, se pueden modelar los dos extremos del conductor como placas paralelas, de manera que la magnitud del campo eléctrico en todo el conductor sea constante en magnitud y dirección y tenga la fuerza dada por:\[\begin{aligned} E=\frac{\Delta V}{L}\end{aligned}\] Combinando esto con la Ley de Ohm, tenemos:\[\begin{aligned} j&=\sigma E\\ \therefore j&=\sigma\frac{\Delta V}{L}\\\end{aligned}\] Dado que la densidad de corriente es una cantidad microscópica, podemos reemplazarla con la corriente,\(I\), una cantidad macroscópica, para el conductor de área transversal,\(A\), para encontrar:\[\begin{aligned} j&=\frac{I}{A}\\ \therefore I&=jA=\sigma\frac{\Delta V}{L}A\end{aligned}\] Esta última ecuación a menudo se escribe aislando la diferencia de potencial:
\[\Delta V=\rho\frac{L}{A}I\]
donde sustituimos la inversa de la conductividad por la resistividad. Esta última ecuación es el equivalente a la Ley de Ohm, pero escrita para una resistencia (macroscópica) de longitud\(L\),, área de sección transversal\(A\), y hecha de un material con resistividad,\(\rho\). Escrito de esta manera, la Ley de Ohm es una afirmación de que la corriente a través de una resistencia es proporcional al voltaje aplicado a través de ella. La constante de proporcionalidad,\(R\), se llama la “resistencia”:
\[\Delta V=RI\]
Esta última ecuación suele llamarse “Ley de Ohm”, aunque, técnicamente, la Ley de Ohm es la relación entre la densidad de corriente y el campo eléctrico. Una resistencia es un objeto macroscópico cuya “resistencia” puede caracterizarse por un solo valor,\(R\), su resistencia. La resistencia de una resistencia se puede determinar a partir de sus propiedades macroscópicas (longitud y área de sección transversal) y del material del que está hecha (con una resistividad dada):
\[R=\rho\frac{L}{A}\]
La (derivada) S.I. unidad de resistencia es el “Ohm”,\((\Omega)\).
Ejercicio\(\PageIndex{1}\)
¿Cuáles son las unidades SI de conductividad?
- \(\frac{\Omega}{\text{C}}\)
- \(\frac{1}{\Omega\text{m}}\)
- \(\frac{\text{N}^{2}\Omega}{\text{C}}\)
- \(\frac{\text{C}}{\text{s}}\)
- Responder
-
El modelo para describir la resistencia de un conductor al flujo de corriente eléctrica bajo una diferencia de potencial fija,\(\Delta V\), es idéntico al modelo que derivamos en la Sección 15.3 para describir el flujo de Poiseuille,\(Q\), de un fluido viscoso incompresible en una tubería con resistencia,\(R\), bajo una diferencia de presión,\(\Delta P\):\[\begin{aligned} \Delta P = RQ\end{aligned}\] Así, se puede pensar en la corriente eléctrica por analogía al flujo incompresible de un fluido viscoso a través de una tubería. Si la tubería es más larga, se opone a más resistencia al flujo de líquido, así como una resistencia más larga tiene una mayor resistencia a la corriente. Una tubería con un área de sección transversal mayor tiene menos resistencia al flujo de líquido, al igual que una resistencia con un área de sección transversal más grande\(A\), tiene una menor resistencia.
Combinar resistencias
Las resistencias son el componente más común en los circuitos, y a continuación mostramos cómo modelar la resistencia equivalente de dos resistencias que se combinan en “paralelo” o en “serie”.
La figura\(\PageIndex{2}\) muestra dos resistencias,\(R_1\) y\(R_2\), conectadas en “serie”, para formar una resistencia efectiva con resistencia,\(R_{eff}\). Una diferencia de potencial,\(\Delta V\), se aplica a través de la combinación de resistencias.
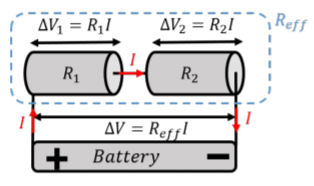
Por analogía con la mecánica de fluidos, las cargas que ingresan a la resistencia\(R_1\),, deben salir de la resistencia a la misma velocidad, y luego cruzar la segunda resistencia,\(R_2\). En otras palabras, lo que entra\(R_1\) debe volver a salir\(R_2\), ya que no hay lugar para que vayan los cargos. Este es el equivalente eléctrico de “continuidad” en mecánica de fluidos. Cuando las resistencias se combinan en serie, ambas resistencias tendrán la misma corriente,\(I\), a través de ellas.
La Ley de Ohm (la versión macroscópica), también debe ser cierta para cada resistencia:\[\begin{aligned} \Delta V_1 &= R_1I\\ \Delta V_2 &= R_2I\end{aligned}\] dónde\(\Delta V_1\) y\(\Delta V_2\), son las diferencias de potencial a través de cada resistencia. \(\Delta V_1\)y\(\Delta V_2\) debe sumar a\(\Delta V\):\[\begin{aligned} \Delta V_1 + \Delta V_2=\Delta V\end{aligned}\] ya que la energía potencial (por unidad de carga) que se pierde en cada resistor debe ser igual a la energía potencial total (por unidad de carga) que se pone a disposición por la batería. Combinando esta última ecuación con la Ley de Ohm para cada resistor, podemos modelar la combinación en serie de resistencias como teniendo una “resistencia efectiva”\(R_{eff}\), dada por:
\[\begin{aligned}\Delta V=\Delta V_{1}+\Delta V_{2}=R_{1}I+R_{2}I=(R_{1}+R_{2})I=R_{eff}I \end{aligned}\]
\[R_{eff}=R_{1}+R_{2}\quad\text{(Series resistors)}\]
Tiene sentido que la resistencia equivalente se encuentre sumando las dos resistencias, cuando éstas están en serie. Si las dos resistencias están hechas del mismo material y tienen la misma área de sección transversal, combinarlas en serie equivale a fabricar una resistencia más larga con las dos longitudes agregadas juntas. El resultado se extiende fácilmente a cualquier número de resistencias:\[\begin{aligned} R_{eff}&=R_1+R_2+R_2+\dots\end{aligned}\]
La figura\(\PageIndex{3}\) muestra dos resistencias, con resistencias\(R_1\) y\(R_2\), combinadas en paralelo para formar una resistencia efectiva con resistencia,\(R_{eff}\). Una diferencia de potencial,\(\Delta V\), se aplica a través de la combinación de resistencias. Cuando las resistencias se combinan en paralelo, ambas resistencias tienen la misma diferencia de potencial entre ellas.
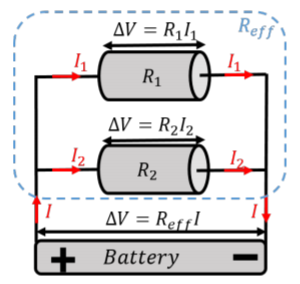
Aplicando la Ley de Ohm a cada resistor, encontramos que cada una de ellas tiene corrientes de diferencia que las atraviesan:\[\begin{aligned} I_1&=\frac{\Delta V}{R_1}\\ I_2&=\frac{\Delta V}{R_2}\end{aligned}\]
La corriente total,\(I\), que entra en la combinación de resistencias, también debe salir de la combinación de resistencia (continuidad), de manera que la corriente total,\(I\), es la suma de la corriente a través de cada resistor:\[\begin{aligned} I=I_1+I_2\end{aligned}\] Combinando esto con la Ley de Ohm, encontramos:\[\begin{aligned} I&=I_1+I_2=\frac{\Delta V}{R_1}+\frac{\Delta V}{R_2}=\left( \frac{1}{R_1}+\frac{1}{R_2} \right)\Delta V\\ \therefore \Delta V &= \frac{1}{\frac{1}{R_1}+\frac{1}{R_2}}I\end{aligned}\] Así, la resistencia efectiva,\(R_{eff}\), de dos resistencias conectadas en paralelo viene dada por:
\[R_{eff}=\frac{1}{\frac{1}{R_{1}}+\frac{1}{R_{2}}}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}\quad\text{(Parallel resistors)}\]
donde las dos formas que se dan son equivalentes. La resistencia efectiva de dos resistencias en paralelo es menor que la resistencia de cualquiera de las resistencias. Esto tiene sentido, porque combinar resistencias en paralelo es análogo a fabricar una sola resistencia con un área de sección transversal mayor, lo que permite “más espacio” para que fluyan las cargas. Nuevamente, este resultado se extiende fácilmente para más de dos resistencias:\[\begin{aligned} R_{eff}=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\dots}\end{aligned}\]
Ejemplo\(\PageIndex{1}\)
Se coloca una\(R_2=2\Omega\) resistencia en paralelo con una\(R_3=3\Omega\) resistencia y la combinación se coloca en serie con una\(R_1=1\Omega\) resistencia, como se muestra en la Figura\(\PageIndex{4}\). ¿Cuál es la resistencia efectiva de esta combinación?
Solución:
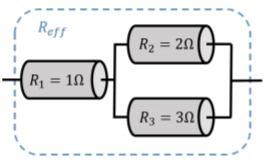
Para determinar la resistencia efectiva de la combinación, primero podemos combinar las resistencias paralelas\(R_2\) y\(R_3\) en una resistencia efectiva\(R'\), que luego podemos combinar en serie con la resistencia\(R_1\), para obtener el resistencia efectiva de las tres resistencias. Primero, combinando las resistencias paralelas,\(R_2\) y\(R_3\), encontramos: Luego\[\begin{aligned} R'=\frac{R_2R_3}{R_2+R_3}=\frac{6}{5}\Omega\end{aligned}\] podemos combinar esto en serie con\(R_1\), para obtener la resistencia efectiva total de la combinación de tres resistencias:\[\begin{aligned} R_{eff}=R_1+R'=\frac{11}{5}\Omega\end{aligned}\]
Discusión:
En este ejemplo, mostramos cómo determinar la resistencia efectiva de una combinación de resistencias en serie y paralelas. Podemos determinar la resistencia efectiva de combinaciones complejas de resistencias de la misma manera, primero combinando subconjuntos de resistencias y luego incluyendo aquellas con otras resistencias.
Energía eléctrica disipada en resistencias
Como discutimos en la Sección 19.2, las cargas que se mueven a través de una resistencia no ganan energía cinética. En cambio, la energía potencial eléctrica disponible a partir del voltaje aplicado a través de la resistencia se convierte en calor, como resultado de cargas que chocan con átomos en el material. La energía potencial neta,\(\Delta U\), disponible para una sola carga,\(q\), viene dada por:\[\begin{aligned} \Delta U=q\Delta V\end{aligned}\] Si hay muchas cargas pasando por la resistencia, la velocidad,\(P\), a la que disiparán la energía en la resistencia viene dada por:\[\begin{aligned} P&=\frac{d}{dt}\Delta U=\frac{d}{dt}q\Delta V=I\Delta V\\ \therefore P&=I\Delta V\end{aligned}\] donde nosotros reconoció que\(dq/dt=I\), es la definición de corriente. \(P\)corresponde a la velocidad a la que se disipa la energía en la resistencia, y tiene dimensiones de potencia. Combinando esto con la Ley de Ohm, la potencia que se disipa en una resistencia se puede escribir de diferentes maneras:
\[P=I\Delta V=\frac{(\Delta V)^{2}}{R}=I^{2}R\]
Ejemplo\(\PageIndex{2}\)
Un secador de pelo está clasificado como consumidor\(1500\text{W}\) when connected to an outlet with a \(120\text{V}\) potential difference. What is the resistance of the hair-dryer, and how much current goes through it when it is running?
Solución:
Dado que se conoce la potencia del secador de pelo y la diferencia de potencial a través de él, podemos determinar fácilmente su resistencia:\[\begin{aligned} P&=\frac{(\Delta V)^2}{R}\\ \therefore R&=\frac{(\Delta V)^2}{P}=\frac{(120\text{V})^2}{(1500\text{W})}=9.6\Omega\end{aligned}\] De igual manera, podemos determinar la corriente a través del secador de pelo:\[\begin{aligned} P&=I\Delta V\\ \therefore I &=\frac{P}{\Delta V}=\frac{(1500\text{W})}{(120\text{V})}=12.5\text{A}\end{aligned}\]
Discusión:
La mayoría de los electrodomésticos están clasificados por la energía eléctrica que consumen. Esta clasificación supone que el aparato estará conectado a una diferencia de potencial fija (\(120\text{V}\)en Norteamérica), por lo que es sencillo determinar la corriente que extraerán. Esto es importante, porque la corriente que extrae el aparato tiene que pasar por el cableado de la casa, y si la corriente es demasiado grande, el cableado (que tiene resistencia) se calentará (\(P=I^2R\)) lo que podría provocar un incendio eléctrico. Los circuitos en una casa cuentan con dispositivos de seguridad (fusibles o disyuntores) que están diseñados para interrumpir el circuito si la corriente es demasiado grande.
Uno puede calificar una fuente de alimentación, como una batería, por la cantidad de energía que puede entregar. Las fuentes de alimentación generalmente están diseñadas para suministrar una diferencia de potencial fija; por ejemplo, una\(9\text{V}\) batería suministra un voltaje constante de\(9\text{V}\). Si se conecta una pequeña resistencia a través de los terminales de la batería, una corriente grande,\(I\), fluirá a través de la resistencia. En principio, la corriente a través de la resistencia vendrá dada por la Ley de Ohm,\(I=\Delta V/R\). Sin embargo, al reducir la resistencia, la corriente aumentará, y la potencia disipada por la resistencia\(P=I\Delta V\), aumentaría indefinidamente. Obviamente, esto no es posible, ya que requiere que la batería suministre energía a la misma tasa cada vez mayor. En la práctica, a medida que disminuye la resistencia, la corriente a través de la resistencia solo aumentará hasta que\(I \Delta V\) sea igual a la potencia máxima que puede disipar la batería. A medida que la resistencia a través de la batería disminuye aún más, el voltaje a través de la batería comenzará a disminuir también, de modo que la potencia disipada en la resistencia\(\Delta V I\),, no exceda la potencia que la batería posiblemente podría suministrar.
Superconductores
Los superconductores son materiales que, bajo ciertas condiciones, tienen resistividad cero. Una resistencia hecha de un material superconductor tendrá, por lo tanto, resistencia cero. Está más allá del alcance de este libro de texto describir cómo surge la superconductividad en los materiales, sin embargo, vale la pena saber que estos existen. Típicamente, la superconductividad surge en los materiales cuando se enfrían a temperaturas cercanas al cero absoluto, aunque algunos materiales exhiben superconductividad a temperaturas mucho más altas (\(\sim 140^{\circ}\text{K}\)o\(\sim -130^{\circ}\text{C}\)). Los materiales superconductores se utilizan a menudo cuando se necesita una gran corriente eléctrica, como en un potente electroimán. Al no tener resistencia, se puede sostener una gran corriente sin disipar ninguna potencia.


