21.5: El efecto Hall

La figura\(\PageIndex{1}\) muestra un circuito sencillo para ilustrar el efecto Hall. Una losa plana de metal, con anchura,\(w\), está conectada a una batería, de manera que la corriente fluye a través de la losa. La losa se sumerge en un campo magnético uniforme\(\vec B\),, que es perpendicular al plano de la losa.

Figura\(\PageIndex{1}\): Ilustración del efecto Hall, a medida que los electrones fluyen a través de una losa que se encuentra inmersa en un campo magnético, la fuerza magnética los empuja hacia un lado, creando una diferencia de potencial eléctrico\(∆V_{Hall}\), transversal al movimiento de la corriente a través de la losa.

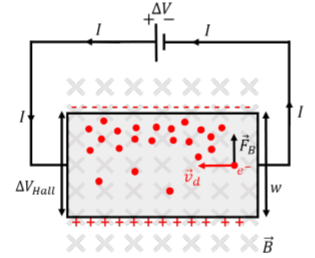
A medida que los electrones ingresan por el lado derecho de la losa (Figura\(\PageIndex{1}\)) y se desplazan hacia la izquierda, experimentarán una fuerza ascendente desde el campo magnético. A medida que se mueven hacia la izquierda a través de la losa, también se mueven hacia arriba y se “amontonan” en ese lado de la losa. Así, habrá un exceso de carga negativa en el lado superior de la losa, lo que dará lugar a una diferencia de potencial eléctrico entre la parte superior y la parte inferior de la losa. Esta diferencia de potencial se llama el “Potencial Hall”,\(\Delta V_{Hall}\). Se alcanza rápidamente un equilibrio entre la fuerza magnética y la fuerza eléctrica asociada al potencial Hall, de manera que el potencial Hall permanece constante.

Si modelamos la losa como dos placas paralelas, con una diferencia de potencial\(\Delta V_{Hall}\),, entre ellas, el campo eléctrico en la losa es constante y dado por:\[\begin{aligned} E= \frac{\Delta V_{Hall}}{w}\end{aligned}\] La condición de equilibrio (que la fuerza eléctrica sobre un electrón es igual a la fuerza magnética) viene dada por:\[\begin{aligned} F_E &= F_B\\ eE &= ev_dB\\ \frac{\Delta V_{Hall}}{w} &= v_d B\\ \therefore \Delta V_{Hall}&= v_d wB\end{aligned}\] Si el se conoce la velocidad de deriva de los electrones, entonces el efecto Hall se puede utilizar para medir la intensidad del campo magnético simplemente midiendo el voltaje Hall. Esta es la forma más común de medir la intensidad de un campo magnético (y el dispositivo para hacerlo se llama sonda Hall). Por el contrario, si se conoce el campo magnético, se puede utilizar el efecto Hall para caracterizar la velocidad de deriva de los electrones y otras cantidades microscópicas para el material del que está hecha la sonda Hall.

El efecto Hall nos permite determinar que son las cargas negativas las que fluyen, y no las cargas positivas. En efecto, considere Figura\(\PageIndex{1}\), pero sustituya los electrones con cargas positivas que fluyen hacia la derecha, lo que equivale en lo que respecta al análisis del circuito. En este caso, esas cargas positivas serán desviadas hacia arriba. Así, si fluyen cargas positivas, el lado superior de la sonda Hall se vuelve positivo, mientras que se vuelve negativo si son cargas negativas las que fluyen. Al medir el signo del potencial Hall, se puede demostrar que son los electrones los que fluyen en una corriente eléctrica.