14.4: Entropía

objetivos de aprendizaje

• Calcular el cambio total en la entropía para un sistema en un proceso reversible

En este y siguientes Átomos, estudiaremos la entropía. Al examinarlo, veremos que las direcciones asociadas a la segunda ley —la transferencia de calor de caliente a frío, por ejemplo— están relacionadas con la tendencia en la naturaleza de que los sistemas se desordenen y que haya menos energía disponible para su uso como trabajo. De hecho, se puede demostrar que la entropía de un sistema es una medida de su desorden y de la indisponibilidad de energía para hacer el trabajo.

Definición de Entropía

Podemos ver cómo se define la entropía recordando nuestra discusión sobre el motor Carnot. _{Señalamos que para un ciclo de Carnot, y por lo tanto para cualquier proceso reversible, Q c /Q h =T c/T h.} Reordenando los rendimientos de términos\(\mathrm{\frac{Q_c}{T_c}=\frac{Q_h}{T_h}}\) para cualquier proceso reversible. Q _c y Q _h son valores absolutos de la transferencia de calor a temperaturas T _c y T _h, respectivamente. Esta relación de Q/T se define como el cambio en la entropía ΔS para un proceso reversible,

\[\mathrm{ΔS=(\dfrac{Q}{T})_{rev},}\]

donde Q es la transferencia de calor, que es positiva para la transferencia de calor hacia y negativa para la transferencia de calor fuera de, y T es la temperatura absoluta a la que se lleva a cabo el proceso reversible. La unidad SI para entropía es julios por kelvin (J/K). Si la temperatura cambia durante el proceso, entonces suele ser una buena aproximación (para pequeños cambios de temperatura) tomar T para ser la temperatura promedio, evitando la necesidad de usar cálculo integral para encontrar ΔS.

La definición de ΔS es estrictamente válida solo para procesos reversibles, como los utilizados en un motor Carnot. Sin embargo, podemos encontrar ΔS precisamente incluso para procesos reales e irreversibles. El motivo es que la entropía S de un sistema, como la energía interna U, depende únicamente del estado del sistema y no de cómo alcanzó esa condición. La entropía es una propiedad del estado. Así, el cambio en la entropía ΔS de un sistema entre el estado uno y el estado dos es el mismo sin importar cómo se produzca el cambio. Solo necesitamos encontrar o imaginar un proceso reversible que nos lleve del estado uno al estado dos y calcular ΔS para ese proceso. Ese será el cambio en la entropía para cualquier proceso que vaya del estado uno al estado dos.

Cambio en la Entropía: Cuando un sistema pasa del estado uno al estado dos, su entropía cambia en la misma cantidad ΔS, ya sea que se siga una ruta hipotética reversible o se tome una ruta irreversible real.

Ejemplo

Ahora echemos un vistazo al cambio en la entropía de un motor Carnot y sus depósitos de calor para un ciclo completo. El reservorio caliente tiene una pérdida de entropía δSH=−Q _{h /T h}, debido a que la transferencia de calor se produce fuera de él (recuerde que cuando el calor se transfiere hacia afuera, entonces Q tiene un signo negativo). El reservorio frío tiene una ganancia de entropía ΔS _c =Q c/T _c, debido a que se produce transferencia de calor en él. (Suponemos que los embalses son lo suficientemente grandes como para que sus temperaturas sean constantes.) Así que el cambio total en la entropía es

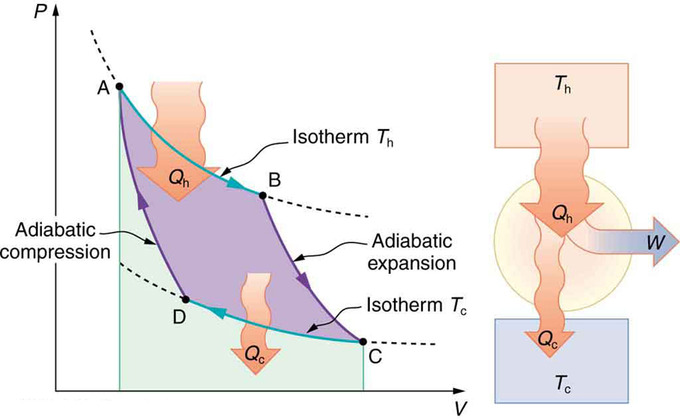
Diagrama PV para un Ciclo Carnot: Diagrama PV para un ciclo Carnot, empleando solo procesos reversibles isotérmicos y adiabáticos. La transferencia de calor Qh ocurre dentro de la sustancia de trabajo durante la trayectoria isotérmica AB, la cual tiene lugar a temperatura constante Th. La transferencia de calor Qc ocurre fuera de la sustancia de trabajo durante la trayectoria isotérmica CD, la cual tiene lugar a temperatura constante Tc. La salida neta de trabajo W es igual al área dentro de la trayectoria ABCDA. También se muestra un esquema de un motor Carnot que opera entre depósitos fríos y calientes a temperaturas Th y Tc.

\[\mathrm{ΔS_{tot}=ΔS_h+ΔS_c.}\]

Así, como sabemos que Q _h /T _h =Q _{c/T c} para un motor Carnot,

\[\mathrm{ΔS_{tot}=−\dfrac{Q_h}{T_h}+\dfrac{Q_c}{T_c}=0.}\]

Este resultado, que tiene validez general, significa que el cambio total en la entropía para un sistema en cualquier proceso reversible es cero.

Interpretación Estástica de la Entropía

Según la segunda ley de la termodinámica, el desorden es muchísimo más probable que el orden.

objetivos de aprendizaje

• Calcular el número de microestados para configuraciones simples

Las diversas formas de formular la segunda ley de la termodinámica dicen lo que sucede más que por qué sucede. ¿Por qué debería ocurrir la transferencia de calor solo de caliente a frío? ¿Por qué el universo debería volverse cada vez más desordenado? La respuesta es que se trata de una cuestión de probabilidad abrumadora. El trastorno es simplemente mucho más probable que el orden. Para ilustrar este hecho, examinaremos algunos procesos aleatorios, comenzando con lanzamientos de monedas.

Lazos de monedas

¿Cuáles son los posibles resultados de lanzar 5 monedas? Cada moneda puede aterrizar ya sea cabeza o cola. A gran escala, nos preocupa sólo el total de cabezas y colas y no por el orden en que aparecen las cabezas y las colas. La siguiente tabla muestra todas las posibilidades junto con números de configuraciones posibles (o microestado; una descripción detallada de cada elemento de un sistema). Por ejemplo, 4 cabezas y 1 instancia de cola pueden ocurrir en 5 configuraciones diferentes, con cualquiera de las 5 monedas mostrando cola y todas las cabezas de descanso. (HHHHT, HHHTH, HHTHH, HTHHH, THHHH)

• 5 cabezas, 0 colas: 1 microestado
• 4 cabezas, 1 cola: 5 microestados
• 3 cabezas, 2 colas: 10 microestados
• 2 cabezas, 3 colas: 10 microestados
• 1 cabeza, 4 colas: 5 microestados
• 0 cabeza, 5 colas: 1 microestado

Obsérvese que todas estas conclusiones se basan en el supuesto crucial de que cada microestado es igualmente probable. De lo contrario, el análisis será erróneo.

Las dos posibilidades más ordenadas son 5 cabezas o 5 colas. (Están más estructurados que los demás.) También son los menos probables, sólo 2 de 32 posibilidades. Las posibilidades más desordenadas son 3 cabezas y 2 colas y su reverso. (Son los menos estructurados) Las posibilidades más desordenadas son también las más probables, con 20 de 32 posibilidades para las 3 cabezas y 2 colas y su reverso. Si empezamos con una matriz ordenada como 5 cabezas y tiramos las monedas, es muy probable que obtengamos como resultado una matriz menos ordenada, ya que 30 de las 32 posibilidades son menos ordenadas. Entonces, aunque comiences con un estado ordenado, existe una fuerte tendencia a pasar del orden al desorden, de baja entropía a alta entropía. Puede suceder lo contrario, pero es poco probable.

Este resultado se vuelve dramático para sistemas más grandes. Considera lo que pasa si tienes 100 monedas en lugar de solo 5. Los arreglos más ordenados (más estructurados) son 100 cabezas o 100 colas. El menos ordenado (menos estructurado) es el de 50 cabezas y 50 colas. Solo hay 1 vía (1 microestado) para obtener la disposición más ordenada de 100 cabezales. El número total de diferentes formas en las que se pueden arrojar 100 monedas, es un impresionante tamaño de 1.27×10 ³⁰. Ahora bien, si empezamos con un macroestado ordenado como 100 cabezas y tiramos las monedas, hay una certeza virtual de que obtendremos un macroestado menos ordenado. Si arrojaste las monedas una vez cada segundo, ¡podrías esperar obtener 100 cabezas o 100 colas una vez en 2×10 ²² años! En contraste, hay un 8% de probabilidad de conseguir 50 cabezas, un 73% de probabilidad de obtener de 45 a 55 cabezas, y un 96% de probabilidad de obtener de 40 a 60 cabezas. El trastorno es muy probable.

Gas Real

El fantástico crecimiento de las probabilidades favoreciendo el desorden que vemos al pasar de 5 a 100 monedas continúa a medida que aumenta el número de entidades en el sistema. En un volumen de 1 m ³, aproximadamente 10 ²³ moléculas (o el orden de magnitud del número de Avogadro) están presentes en un gas. Las condiciones más probables (o macroestado) para el gas son las que vemos todo el tiempo, una distribución aleatoria de átomos en el espacio con una distribución Maxwell-Boltzmann de velocidades en direcciones aleatorias, como lo predice la teoría cinética como se muestra en (a). Esta es la condición más desordenada y menos estructurada que podamos imaginar.

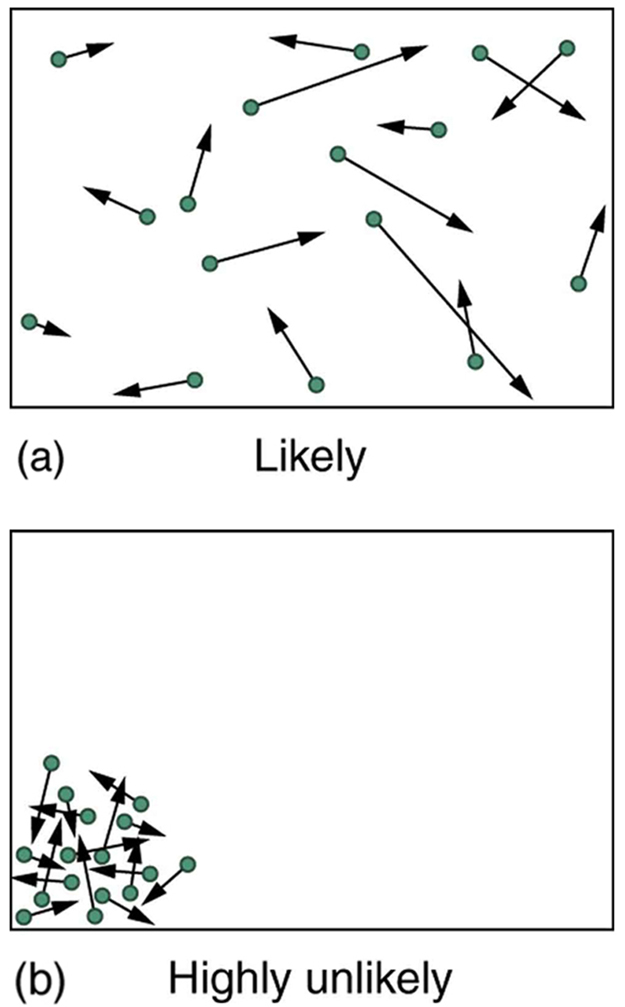
Teoría cinética: a) El estado ordinario del gas en un contenedor es una distribución desordenada y aleatoria de átomos o moléculas con una distribución de velocidades Maxwell-Boltzmann. Es tan improbable que estos átomos o moléculas terminen alguna vez en una esquina del contenedor que bien podría ser imposible. (b) Con la transferencia de energía, el gas puede ser forzado a entrar en una esquina y reducir considerablemente su entropía. Pero dejada sola, aumentará espontáneamente su entropía y volverá a las condiciones normales, porque son inmensamente más probables.

En contraste, un tipo de macroestado muy ordenado y estructurado tiene todos los átomos en una esquina de un contenedor con velocidades idénticas. Hay muy pocas formas de lograr esto (muy pocos microestados que le corresponden), por lo que es extremadamente improbable que ocurra. (Véase b).) En efecto, es tan improbable que tengamos una ley que diga que es imposible, lo que nunca se ha observado que sea violada —la segunda ley de la termodinámica.

Orden a Trastorno

La entropía es una medida del trastorno, por lo que el aumento de la entropía significa más trastorno en el sistema.

objetivos de aprendizaje

• Discutir entropía y trastorno dentro de un sistema

La entropía es una medida del trastorno. Esta noción fue postulada inicialmente por Ludwig Boltzmann en el siglo XIX. Por ejemplo, fundir un bloque de hielo significa tomar un sistema altamente estructurado y ordenado de moléculas de agua y convertirlo en un líquido desordenado en el que las moléculas no tienen posiciones fijas. Hay un gran incremento en la entropía en el proceso.

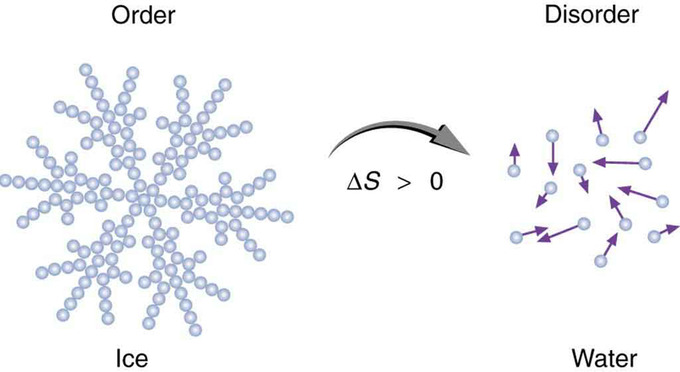
Entropía de Hielo: Cuando el hielo se derrite, se vuelve más desordenado y menos estructurado. La disposición sistemática de las moléculas en una estructura cristalina es reemplazada por un movimiento más aleatorio y menos ordenado de moléculas sin ubicaciones u orientaciones fijas. Su entropía aumenta debido a que la transferencia de calor se produce en ella. La entropía es una medida del trastorno.

Ejemplo\(\PageIndex{1}\):

Como ejemplo, supongamos que mezclamos masas iguales de agua originalmente a dos temperaturas diferentes, digamos 20.0º C y 40.0º C. El resultado es agua a una temperatura intermedia de 30.0º C. Tres resultados han resultado:

• La entropía ha aumentado.
• Algo de energía se ha vuelto indisponible para hacer el trabajo.
• El sistema se ha vuelto menos ordenado.

Entropía, Energía y Trastorno

Pensemos en cada uno de los resultados. En primer lugar, la entropía ha aumentado por la misma razón que lo hizo en el ejemplo anterior. Mezclar los dos cuerpos de agua tiene el mismo efecto que la transferencia de calor de la caliente y la misma transferencia de calor a la fría. La mezcla disminuye la entropía del agua caliente pero aumenta la entropía del agua fría en mayor cantidad, produciendo un aumento general de la entropía.

Segundo, una vez que se mezclan las dos masas de agua, solo hay una temperatura; no se puede hacer funcionar un motor térmico con ellas. La energía que podría haber sido utilizada para hacer funcionar un motor térmico ahora no está disponible para hacer trabajo.

Tercero, la mezcla es menos ordenada, o para usar otro término, menos estructurada. En lugar de tener dos masas a diferentes temperaturas y con diferentes distribuciones de velocidades moleculares, ahora tenemos una sola masa con una temperatura uniforme.

Estos tres resultados —entropía, falta de disponibilidad de energía y desorden— no solo están relacionados, sino que de hecho son esencialmente equivalentes.

Muerte por Calor

La entropía del universo va en constante aumento y está destinada al equilibrio termodinámico, llamado la muerte por calor del universo.

objetivos de aprendizaje

• Describir procesos que conducen a la muerte por calor del universo

En el universo temprano, energético, toda la materia y la energía eran fácilmente intercambiables e idénticas en naturaleza. La gravedad jugó un papel vital en el universo joven. Aunque puede haber parecido desordenado, había una enorme energía potencial disponible para hacer el trabajo, toda la energía futura en el universo.

A medida que el universo maduraba, surgieron diferencias de temperatura, lo que creó más oportunidades para el trabajo. Las estrellas son más calientes que los planetas, por ejemplo, que son más cálidas que los asteroides helados, que aún son más cálidas que el vacío del espacio entre ellas. La mayoría de estos se están enfriando por sus nacimientos generalmente violentos, momento en el que se les proporcionó energía propia: energía nuclear en el caso de las estrellas, energía volcánica en la Tierra y otros planetas, y así sucesivamente. Sin aporte de energía adicional, sin embargo, sus días están contados.

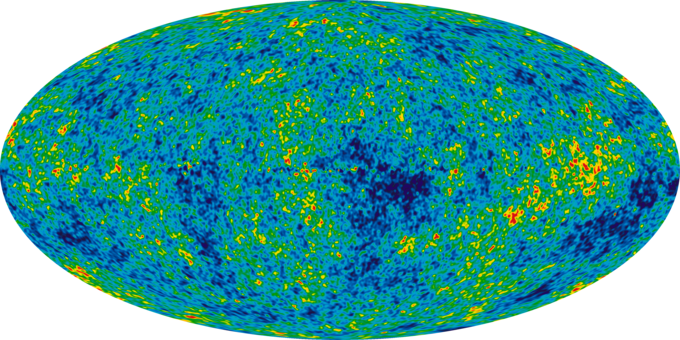
Universo Infantil: La imagen de un universo infantil revela fluctuaciones de temperatura (mostradas como diferencias de color) que corresponden a las semillas que crecieron hasta convertirse en las galaxias.

A medida que aumenta la entropía, cada vez hay menos energía disponible en el universo para hacer el trabajo. En la Tierra, todavía tenemos grandes reservas de energía como los combustibles fósiles y nucleares; diferencias de temperatura a gran escala, que pueden proporcionar energía eólica; energías geotérmicas por diferencias de temperatura en las capas terrestres; y energías mareales debido a nuestra abundancia de agua líquida. A medida que estos se utilizan, una cierta fracción de la energía que contienen nunca se puede convertir en hacer trabajo. Eventualmente, todos los combustibles se agotarán, todas las temperaturas se igualarán, y será imposible que los motores térmicos funcionen, o que se haga el trabajo.

Dado que el universo es un sistema cerrado, la entropía del universo aumenta constantemente, por lo que la disponibilidad de energía para hacer el trabajo disminuye constantemente. Finalmente, cuando todas las estrellas han muerto, se han utilizado todas las formas de energía potencial, y todas las temperaturas se han igualado (dependiendo de la masa del universo, ya sea a una temperatura muy alta después de una contracción universal, o a una muy baja, justo antes de que cese toda actividad) no habrá posibilidad de hacer el trabajo.

De cualquier manera, el universo está destinado al equilibrio termodinámico, máxima entropía. Esto a menudo se llama la muerte por calor del universo, y significará el fin de toda actividad. No obstante, ya sea que el universo se contraiga y se caliente, o continúe expandiéndose y enfriándose, el final no está cerca. Los cálculos de los agujeros negros sugieren que la entropía puede continuar fácilmente durante al menos 10 ¹⁰⁰ años.

Sistemas Vivos y Evolución

Es posible que la entropía de una parte del universo disminuya, siempre que el cambio total en la entropía del universo aumente.

objetivos de aprendizaje

• Formular condiciones que permitan disminuir la entropía en una parte del universo

Algunas personas malinterpretan la segunda ley de la termodinámica, aseverada en términos de entropía, para decir que el proceso de la evolución de la vida viola esta ley. Con el tiempo, los organismos complejos evolucionaron a partir de ancestros mucho más simples, lo que representa una gran disminución en la entropía de la biosfera terrestre. Es un hecho que los organismos vivos han evolucionado para estar altamente estructurados, y mucho más bajos en entropía que las sustancias de las que crecen. Pero siempre es posible que la entropía de una parte del universo disminuya, siempre y cuando aumente el cambio total en la entropía del universo. En forma de ecuación, podemos escribir esto como

\[\mathrm{ΔS_{tot}=ΔS_{sys}+ΔS_{env}>0.}\]

Así ΔS _sys puede ser negativo siempre que ΔS _env sea positivo y mayor en magnitud.

¿Cómo es posible que un sistema disminuya su entropía? La transferencia de energía es necesaria. Si recojo mineral de hierro del suelo y lo convierto en acero y construyo un puente, mi trabajo (y energía utilizada) ha disminuido la entropía de ese sistema. La energía proveniente del Sol puede disminuir la entropía de los sistemas locales en la Tierra, es decir, ΔS _sys es negativo. Pero la entropía general del resto del universo aumenta en mayor cantidad, es decir, ΔS _env es positivo y de mayor magnitud. Así, ΔS _tot >0, y la segunda ley de la termodinámica no es violada.

Cada vez que una planta almacena algo de energía solar en forma de energía potencial química, o una corriente ascendente de aire caliente levanta a un ave altísima, la Tierra puede verse como un motor térmico que opera entre un depósito caliente suministrado por el Sol y un depósito frío suministrado por el espacio exterior oscuro, un motor térmico de alta complejidad, causando disminuciones locales en la entropía ya que utiliza parte de la transferencia de calor del Sol al espacio profundo. Sin embargo, hay un gran aumento total en la entropía resultante de esta transferencia masiva de calor. Una pequeña parte de esta transferencia de calor se almacena en sistemas estructurados en la Tierra, produciendo disminuciones locales mucho menores en la entropía.

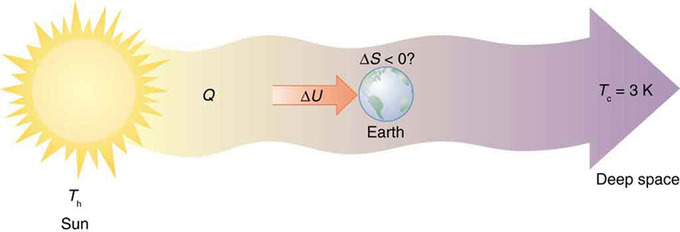
Entropía de la Tierra: La entropía de la Tierra puede disminuir en el proceso de interceptar una pequeña parte de la transferencia de calor del Sol al espacio profundo. La entropía para todo el proceso aumenta mucho mientras que la Tierra se vuelve más estructurada con sistemas vivos y energía almacenada en diversas formas.

Calentamiento global revisado

La Segunda Ley de Termodinámica puede ayudar a explicar el calentamiento global en los últimos 250 años.

objetivos de aprendizaje

• Describir el efecto del calor vertido al ambiente sobre la temperatura atmosférica de la Tierra

La Segunda Ley de la Termodinámica puede ayudar a explicar por qué ha habido aumentos en las temperaturas de la Tierra en los últimos 250 años (a menudo llamado “Calentamiento Global”), y a muchos profesionales les preocupa que el aumento de la entropía del universo sea una amenaza real para el medio ambiente.

Temperatura Global Tierra-Océano: Cambio medio global de la temperatura tierra-océano de 1880 a 2012, relativo a la media de 1951 a 1980. La línea negra es la media anual y la línea roja es la media consecutiva de cinco años. Las barras verdes muestran estimaciones de incertidumbre.

Cuando un motor opera, el calor fluye de un tanque de calor de mayor temperatura a un disipador de calor de menor temperatura. Entre estos estados, el flujo de calor se convierte en energía útil con la ayuda de motores térmicos. A medida que estos motores funcionan, sin embargo, se pierde una gran cantidad de calor para el medio ambiente debido a ineficiencias. En un motor Carnot, que es el motor teórico más eficiente basado en el ciclo Carnot, la eficiencia máxima es igual a uno menos la temperatura del disipador de calor (T _c) dividida por la temperatura de la fuente de calor (T _h).

\[\mathrm{(Eff_c=1−\dfrac{T_c}{T_h}).}\]

Esta relación muestra que para que se logre una mayor eficiencia es necesario que exista la mayor diferencia de temperatura disponible. Esto trae a colación dos puntos importantes: los disipadores de calor optimizados están en cero absoluto, y cuanto más tiempo los motores viertan calor en un sistema aislado, los motores menos eficientes serán.

Desafortunadamente para la eficiencia del motor, la vida cotidiana nunca opera en cero absoluto. En un motor promedio de automóvil, solo del 14% al 26% del combustible que se introduce se usa realmente para hacer que el automóvil avance. Esto significa que de 74% a 86% se pierde calor o se usa para alimentar accesorios. Según el Departamento de Energía de Estados Unidos, 70% a 72% del calor producido por la quema de combustible es calor perdido por el motor. El exceso de calor perdido por el motor se libera luego en el disipador de calor, que en el caso de muchos motores modernos sería la atmósfera de la Tierra. A medida que se arroje más calor al ambiente, la temperatura atmosférica (o disipador de calor) de la Tierra aumentará. Con la entropía del entorno en constante aumento, la búsqueda de nuevas tecnologías más eficientes y nuevos motores no térmicos se ha convertido en una prioridad.

Contaminación Térmica

La contaminación térmica es la degradación de la calidad del agua por cualquier proceso que cambie la temperatura ambiente del agua.

objetivos de aprendizaje

• Identificar factores que conducen a la contaminación térmica y sus efectos ecológicos

La contaminación térmica es la degradación de la calidad del agua por cualquier proceso que cambie la temperatura ambiente del agua. Una causa común de contaminación térmica es el uso del agua como refrigerante, por ejemplo, por parte de centrales eléctricas y fabricantes industriales. Cuando el agua utilizada como refrigerante regresa al ambiente natural a una temperatura más alta, el cambio de temperatura disminuye el suministro de oxígeno y afecta la composición del ecosistema.

Como aprendimos en nuestro Atom sobre “Motores de Calor”, todos los motores térmicos requieren transferencia de calor, lograda al proporcionar (y mantener) la diferencia de temperatura entre la fuente de calor del motor y el disipador de calor. El agua, con su alta capacidad calorífica, funciona extremadamente bien como refrigerante. Pero esto significa que el agua de refrigeración debe reponerse constantemente para mantener su capacidad de enfriamiento.

Torre de enfriamiento: Esta es una torre de enfriamiento en la central eléctrica Gustav Knepper, Dortmund, Alemania. El agua de refrigeración circula dentro de la torre.

Efectos Ecológicos

La temperatura elevada del agua generalmente disminuye el nivel de oxígeno disuelto del agua. Esto puede dañar a los animales acuáticos como peces, anfibios y otros organismos acuáticos. Un aumento de la tasa metabólica puede resultar en menos recursos; los organismos más adaptados que se mueven pueden tener una ventaja sobre los organismos que no están acostumbrados a la temperatura más cálida. Como resultado, las cadenas alimentarias de los entornos antiguos y nuevos pueden verse comprometidas. Algunas especies de peces evitarán segmentos de arroyos o áreas costeras adyacentes a una descarga térmica. Como resultado, la biodiversidad puede disminuir. Muchas especies acuáticas también no podrán reproducirse a temperaturas elevadas.

Algunos pueden suponer que al enfriar el agua caliente, posiblemente podamos solucionar el problema de la contaminación térmica. Sin embargo, como señalamos en nuestro Atom anterior sobre “Bombas de Calor y Refrigeradores”, el trabajo requerido para el enfriamiento adicional conduce a más escape de calor al ambiente. Por lo tanto, empeora aún más la situación.

Puntos Clave

• Esta relación de Q/T se define como el cambio en la entropía ΔS para un proceso reversible: ΔS =( QT) revΔS =( QT) rev.
• La entropía es una propiedad del estado. Por lo tanto, el cambio en la entropía ΔS de un sistema entre dos estados es el mismo sin importar cómo se produzca el cambio.
• El cambio total en la entropía para un sistema en cualquier proceso reversible es cero.
• Cada microestado es igualmente probable en el ejemplo de lanzar monedas. Sin embargo, como macroestado, existe una fuerte tendencia a que ocurra el estado más desordenado.
• Al lanzar 100 monedas, si las monedas se lanzan una vez cada segundo, podría esperar obtener las 100 cabezas o las 100 colas una vez en 2×10 ²² años.
• Las moléculas en un gas siguen la distribución de velocidades de Maxwell-Boltzmann en direcciones aleatorias, que es la condición más desordenada y menos estructurada de todas las posibilidades.
• Mezclar dos sistemas puede disminuir la entropía de un sistema, pero aumentar la entropía del otro sistema en mayor cantidad, produciendo un aumento general de la entropía.
• Después de mezclar agua a dos temperaturas diferentes, la energía en el sistema que podría haberse utilizado para hacer funcionar un motor térmico ahora no está disponible para hacer funcionar. Además, el proceso hizo que todo el sistema fuera más menos estructurado.
• La entropía, la falta de disponibilidad de energía y el trastorno no solo están relacionados, sino que de hecho son esencialmente equivalentes.
• En el universo temprano, energético, toda la materia y la energía eran fácilmente intercambiables e idénticas en naturaleza.
• A medida que aumenta la entropía, cada vez hay menos energía disponible en el universo para hacer el trabajo.
• El universo está destinado al equilibrio termodinámico —máxima entropía. Esto a menudo se llama la muerte por calor del universo, y significará el fin de toda actividad.
• Los organismos vivos han evolucionado para estar altamente estructurados, y mucho más bajos en entropía que las sustancias de las que crecen.
• Es posible que un sistema disminuya su entropía siempre que el cambio total en la entropía del universo aumente: ΔSTOT=ΔSSYs+ΔSENV>0δSTOT=ΔSSYs+ΔSENV>0.
• La Tierra puede ser vista como un motor térmico que opera entre un depósito caliente suministrado por el Sol y un depósito frío suministrado por el espacio exterior oscuro.
• A medida que funcionan los motores térmicos, se pierde una gran cantidad de calor para el medio ambiente debido a ineficiencias.
• Incluso en un motor Carnot, que es el motor teórico más eficiente, hay una pérdida de calor determinada por la relación de temperatura del motor y su entorno.
• A medida que se arroje más calor al ambiente, la temperatura atmosférica de la Tierra aumentará.
• Todos los motores térmicos requieren transferencia de calor, lograda al proporcionar (y mantener) la diferencia de temperatura entre la fuente de calor del motor y el disipador de calor. El agua de refrigeración se usa típicamente para mantener la diferencia de temperatura.
• La temperatura elevada del agua generalmente disminuye el nivel de oxígeno disuelto del agua, afectando la composición del ecosistema.
• Enfriar el agua caliente no es una solución para la contaminación térmica porque se requiere trabajo adicional para el enfriamiento, lo que lleva a más escape de calor al ambiente.

Términos Clave

• Ciclo carnot: Un ciclo termodinámico teórico. Es el ciclo más eficiente para convertir una determinada cantidad de energía térmica en trabajo.
• reversible: Capaz de regresar al estado original sin consumo de energía libre y aumento de entropía.
• trastorno: Ausencia de cierta simetría o correlación en un sistema de muchas partículas.
• Distribución Maxwell-Boltzmann: Una distribución que describe las velocidades de las partículas en gases, donde las partículas se mueven libremente sin interactuar entre sí, excepto por colisiones elásticas muy breves en las que pueden intercambiar impulso y energía cinética.
• entropía: Una medida de cuán uniformemente se distribuye la energía (o alguna propiedad análoga) en un sistema.
• geotérmica: Pertenente a la energía térmica extraída de embalses en el interior de la Tierra.
• asteroide: Un objeto sólido natural, que es más pequeño que un planeta y no es un cometa, que orbita una estrella.
• Ciclo carnot: Un ciclo termodinámico teórico. Es el ciclo más eficiente para convertir una determinada cantidad de energía térmica en trabajo.
• cero absoluto: La temperatura más fría posible: cero en la escala Kelvin y aproximadamente -273.15°C y -459.67°F La ausencia total de calor; la temperatura a la que cesaría el movimiento de todas las moléculas.
• motor térmico: Cualquier dispositivo que convierta la energía térmica en trabajo mecánico.
• bomba de calor: Un dispositivo que transfiere calor de algo a una temperatura más baja a algo a una temperatura más alta haciendo el trabajo.

LICENCIAS Y ATRIBUCIONES

CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

• Curación y Revisión. Proporcionado por: Boundless.com. Licencia: CC BY-SA: Atribución-CompartirIgual

CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

• Colegio OpenStax, Colegio de Física. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Reversible. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/reversible. Licencia: CC BY-SA: Atribución-CompartirIgual
• Ciclo de carnot. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Carnot%20Ciclo. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42235/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42238/latest...ol11406/latest. Licencia: CC BY: Atribución
• Distribución Maxwell-Boltzmann. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Maxwell... 20distribución. Licencia: CC BY-SA: Atribución-CompartirIgual
• trastorno. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/desorden. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42235/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42238/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• trastorno. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/desorden. Licencia: CC BY-SA: Atribución-CompartirIgual
• entropía. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Entropy. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42235/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42238/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• entropía. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Entropy. Licencia: CC BY-SA: Atribución-CompartirIgual
• asteroide. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/asteroid. Licencia: CC BY-SA: Atribución-CompartirIgual
• geotérmica. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/geothermal. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42235/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42238/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Muerte por calor del universo. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Heat_de... f_the_universe. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• entropía. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Entropy. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42235/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42238/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Muerte por calor del universo. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Heat_de... f_the_universe. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• cero absoluto. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/absolute_zero. Licencia: CC BY-SA: Atribución-CompartirIgual
• La entropía y el medio ambiente. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Entropy... he_environment. Licencia: CC BY-SA: Atribución-CompartirIgual
• Ciclo de carnot. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Carnot%20Ciclo. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42235/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42238/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Muerte por calor del universo. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Heat_de... f_the_universe. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Calentamiento global. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Calentamiento Global. Licencia: CC BY: Atribución
• Contaminación térmica. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Thermal_pollution. Licencia: CC BY-SA: Atribución-CompartirIgual
• motor de calor. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/heat_engine. Licencia: CC BY-SA: Atribución-CompartirIgual
• bomba de calor. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/heat_pump. Licencia: CC BY-SA: Atribución-CompartirIgual
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42235/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42238/latest...ol11406/latest. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Muerte por calor del universo. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Heat_de... f_the_universe. Licencia: CC BY: Atribución
• Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42237/latest...ol11406/latest. Licencia: CC BY: Atribución
• Calentamiento global. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Calentamiento Global. Licencia: CC BY: Atribución
• Contaminación térmica. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Thermal_pollution. Licencia: CC BY: Atribución