6.5: Velocidad angular y aceleración angular

. Velocidad Angular

Siempre elegiremos un sistema de coordenadas cilíndricas diestras. Si el eje z positivo apunta hacia arriba, entonces elegimos θ para estar aumentando en sentido contrario a las agujas del reloj como se muestra en las Figuras 6.6.

Figura 6.6 Sistema de coordenadas para diestros

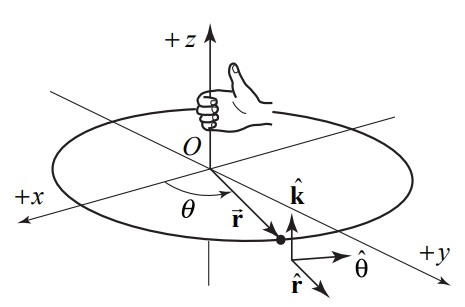
Para un objeto puntual que experimenta movimiento circular alrededor del eje z, el vector de velocidad angular\(\vec{\omega}\) se dirige a lo largo del eje z con componente z igual a la derivada de tiempo del ángulo θ,

\[\vec{\omega}=\frac{d \theta}{d t} \hat{\mathbf{k}}=\omega_{z} \hat{\mathbf{k}} \nonumber \]

Las unidades SI de velocidad angular son\(\left[\mathrm{rad} \cdot \mathrm{s}^{-1}\right]\) Tenga en cuenta que la velocidad angular es solo la magnitud del componente z de la velocidad angular,

\[\omega \equiv\left|\omega_{z}\right|=\left|\frac{d \theta}{d t}\right| \nonumber \]

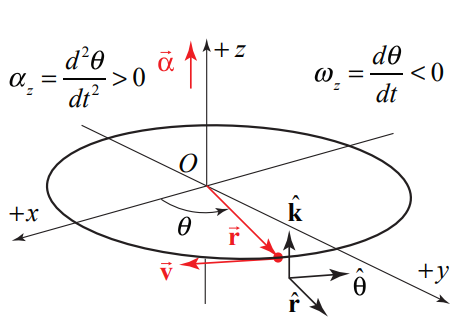
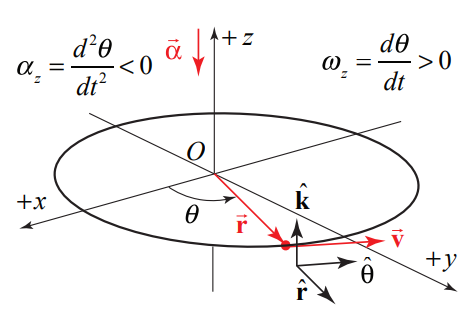
Si la velocidad del objeto está en la\(+\hat{\boldsymbol{\theta}}\) dirección -dirección, (girando en sentido contrario a las agujas del reloj en la Figura 6.7 (a)), entonces el componente z de la velocidad angular es positivo,\(\omega_{z}=d \theta / d t>0\) El vector de velocidad angular luego apunta en la\(+\hat{\mathbf{k}}\) dirección -como se muestra en la Figura 6.7 (a). Si la velocidad del objeto está en la\(-\hat{\boldsymbol{\theta}}\) dirección -dirección, (girando en el sentido de las agujas del reloj en la Figura 6.7 (b)), entonces el componente z de la velocidad angular de la velocidad angular es negativo,\(\omega_{z}=d \theta / d t<0\). El vector de velocidad angular apunta entonces en la\(-\hat{\mathbf{k}}\) dirección -como se muestra en la Figura 6.7 (b).

Figura 6.7 (b) Vector de velocidad angular para movimiento con dθ/dt > 0.

Figura 6.7 (b) Velocidad angular para movimiento con dθ/dt < 0.

La velocidad y la velocidad angular están relacionadas por

\[\overrightarrow{\mathbf{v}}=\overrightarrow{\boldsymbol{\omega}} \times \overrightarrow{\mathbf{r}}=\frac{d \theta}{d t} \hat{\mathbf{k}} \times r \hat{\mathbf{r}}=r \frac{d \theta}{d t} \hat{\boldsymbol{\theta}} \nonumber \]

Ejemplo 6.2 Velocidad angular

Una partícula se mueve en un círculo de radio R. At t = 0, se ubica en el eje x. El ángulo que forma la partícula con el eje x positivo viene dado por\(\theta(t)=A t-B t^{3}\) donde A y B son constantes positivas. Determinar (a) el vector de velocidad angular y (b) el vector de velocidad. Expresa tu respuesta en coordenadas polares. (c) ¿A qué hora\(t=t_{1}\) es cero la velocidad angular? (d) Cuál es la dirección de la velocidad angular para 1. \(t<t_{1}\)2. \(t>t_{1} ?\)?

Solución:

El derivado de\(\theta(t)=A t-B t^{3}\) es

\[\frac{d \theta(t)}{d t}=A-3 B t^{2} \nonumber \]

Por lo tanto, el vector de velocidad angular viene dado por

\[\overrightarrow{\boldsymbol{\omega}}(t)=\frac{d \theta(t)}{d t} \hat{\mathbf{k}}=\left(A-3 B t^{2}\right) \hat{\mathbf{k}} \nonumber \]

La velocidad viene dada por

\[\overrightarrow{\mathbf{v}}(t)=R \frac{d \theta(t)}{d t} \hat{\mathbf{\theta}}(t)=R\left(A-3 B t^{2}\right) \hat{\boldsymbol{\theta}}(t) \nonumber \]

La velocidad angular es cero en el\(t=t_{1}\) momento en que

\[A-3 B t_{1}^{2}=0 \Rightarrow t_{1}=\sqrt{A / 3 B} \nonumber \]

Para de\(t<t_{1}, \frac{d \theta(t)}{d t}=A-3 B t_{1}^{2}>0\) ahí\(\overrightarrow{\boldsymbol{\omega}}(t)\) puntos en la\(\hat{\mathbf{k}}\) dirección positiva.

Para de\(t>t_{1}, \frac{d \theta(t)}{d t}=A-3 B t_{1}^{2}<0\) ahí\(\overrightarrow{\boldsymbol{\omega}}(t)\) puntos en la\(\hat{\mathbf{k}}\) dirección positiva.

Aceleración angular

De manera similar, para un objeto puntual que experimenta movimiento circular alrededor del eje z fijo, la aceleración angular se define como

\[\vec{\alpha}=\frac{d^{2} \theta}{d t^{2}} \hat{\mathbf{k}}=\alpha_{z} \hat{\mathbf{k}} \nonumber \]

Las unidades SI de aceleración angular son\(\left[\mathrm{rad} \cdot \mathrm{s}^{-2}\right]\) La magnitud de la aceleración angular se denota con el símbolo griego alfa,

\[\alpha \equiv|\vec{\alpha}|=\left|\frac{d^{2} \theta}{d t^{2}}\right| \nonumber \]

Hay cuatro casos especiales a considerar para la dirección de la velocidad angular. Primero consideremos los dos tipos de movimiento con\(\overrightarrow{\boldsymbol{\alpha}}\) apuntar en la\(\hat{\mathbf{k}}\) dirección -dirección: (i) si el objeto está girando en sentido antihorario y acelerando entonces ambos\(d \theta / d t>0\) y\(d^{2} \theta / d t^{2}>0\) (Figura 6.8 (a)) (ii) si el objeto está girando en sentido horario y ralentizando entonces\(d \theta / d t<0\) pero\(d^{2} \theta / d t^{2}>0\) ( Figura 6.8 (b). Hay dos casos correspondientes en los que\(\vec{\alpha}\) apuntar en la\(-\hat{\mathbf{k}}\) dirección -dirección (iii) si el objeto está girando en sentido antihorario y desacelerando entonces\(d \theta / d t>0\) pero\(d^{2} \theta / d t^{2}<0\) (Figura 6.9 (a), (iv) si el objeto está girando en sentido horario y acelerando entonces ambos\(d \theta / d t<0\) y\(d^{2} \theta / d t^{2}<0\) (Figura 6.9 b).

Figura 6.8 (a) Vector de aceleración angular para movimiento con\(d \theta / d t>0\), y\(d^{2} \theta / d t^{2}>0\)

Figura 6.8 (b) Vector vectorial de velocidad angular para movimiento con\(d \theta / d t<0\), y\(d^{2} \theta / d t^{2}>0\)

Figura 6.9 (a) Vector de aceleración angular para el movimiento con\(d \theta / d t>0\), y\(d^{2} \theta / d t^{2}<0\)

Figura 6.9 (b) Vector vectorial de velocidad angular para movimiento con\(d \theta / d t<0\), y\(d^{2} \theta / d t^{2}<0\)

Ejemplo 6.3 Integración y Cinemática de Movimiento Circular

Un objeto similar a un punto está restringido para viajar en círculo. El componente z de la aceleración angular del objeto para el intervalo de tiempo\(\left[0, t_{1}\right]\) viene dado por la función

\ [\ alpha_ {z} (t) =\ left\ {\ begin {array} {l}
b\ left (1-\ frac {t} {t_ {1}}\ right); 0\ leq t\ leq t_ {1}\\
0; t>t_ {1}
\ end {array}\ right. \ nonumber\]

donde b es una constante positiva con unidades rad\(\cdot \mathrm{S}^{-2}\).

a) Determinar una expresión para la velocidad angular del objeto a\(t=t_{1}\).

b) ¿A través de qué ángulo ha girado el objeto en el momento\(t=t_{1}\)?

Solución:

a) La velocidad angular en el momento\(t=t_{1}\) viene dada por

\[\omega_{z}\left(t_{1}\right)-\omega_{z}(t=0)=\int_{t^{\prime}=0}^{t^{\prime}=t_{1}} \alpha_{z}\left(t^{\prime}\right) d t^{\prime}=\int_{t^{\prime}=0}^{t^{\prime}=t_{1}} b\left(1-\frac{t^{\prime}}{t_{1}}\right) d t^{\prime}=b\left(t_{1}-\frac{t_{1}^{2}}{2 t_{1}}\right)=\frac{b t_{1}}{2} \nonumber \]

b) Para encontrar el ángulo por el\(\theta\left(t_{1}\right)-\theta(t=0)\) que el objeto ha girado en el momento\(t=t_{1}\), primero es necesario encontrar\(\omega_{z}(t)\) integrando el componente z de la aceleración angular

\[\omega_{z}(t)-\omega_{z}(t=0)=\int_{t^{\prime}=0}^{t^{\prime}=t} \alpha_{z}\left(t^{\prime}\right) d t^{\prime}=\int_{t=0}^{t^{\prime}=t} b\left(1-\frac{t^{\prime}}{t_{1}}\right) d t^{\prime}=b\left(t-\frac{t^{2}}{2 t_{1}}\right) \nonumber \]

Porque partió del descanso,\(\omega_{z}(t=0)=0\), de ahí\(\omega_{z}(t)=b\left(t-\frac{t^{2}}{2 t_{1}}\right) ; 0 \leq t \leq t_{1}\)

Luego integre\(\omega_{z}(t)\) entre t = 0 y\(t=t_{1}\) para encontrar que

\[\theta\left(t_{1}\right)-\theta(t=0)=\int_{t^{\prime}=0}^{t^{\prime}=t_{1}} \omega_{z}\left(t^{\prime}\right) d t^{\prime}=\int_{t^{\prime}=0}^{t^{\prime}=t_{1}} b\left(t^{\prime}-\frac{t^{\prime 2}}{2 t_{1}}\right) d t^{\prime}=b\left(\frac{t_{1}^{2}}{2}-\frac{t_{1}^{3}}{6 t_{1}}\right)=\frac{b t_{1}^{2}}{3} \nonumber \]