8.7: Ejemplos trabajados

Ejemplo 8.7 Escalera

Un objeto de masa m en el tiempo t = 0 tiene velocidad\(v_{0}\) Se desliza una distancia s a lo largo de un piso horizontal y luego fuera de la parte superior de una escalera (Figura 8.35). El coeficiente de fricción cinética entre el objeto y el piso es\(\mu_{\mathrm{k}}\) El objeto golpea en el extremo más alejado de la tercera escalera. Cada escalera tiene un ascenso de h y un recorrido de d. Descuidar la resistencia al aire y usar g para la constante gravitacional. (a) ¿Cuál es la distancia a la que se desliza el objeto a lo largo del piso?

Figura 8.35 Objeto cayendo por una escalera

Solución: Hay dos etapas distintas para el movimiento del objeto, el movimiento horizontal inicial y luego la caída libre. La posición final dada del objeto, en el extremo más alejado de la tercera escalera, determinará la componente horizontal de la velocidad en el instante en que el objeto salió de la parte superior de las escaleras. Esto a su vez se puede utilizar para determinar el tiempo en que el objeto se desaceleró a lo largo del piso, y de ahí la distancia recorrida en el piso. Las cantidades dadas son m, v0, µk, g, h y d.

Para el movimiento horizontal, elija coordenadas con el origen en la posición inicial del bloque. Elija la\(\hat{\mathbf{i}}\) dirección positiva para ser horizontal, dirigida a la izquierda en la Figura 8.35,\(\hat{\mathbf{j}}\) -dirección para ser vertical (arriba). Las fuerzas sobre el objeto son la gravedad,\(m \overrightarrow{\mathbf{g}}=-m g \hat{\mathbf{j}}\) la fuerza normal\(\overrightarrow{\mathbf{N}}=N \hat{\mathbf{j}}\) y la fuerza cinética de fricción\(\overrightarrow{\mathbf{f}}_{\mathrm{k}}=-f_{\mathrm{k}} \hat{\mathbf{i}}\). Los componentes de los vectores en la Segunda Ley de Newton,\(\overrightarrow{\mathbf{F}}=m \overrightarrow{\mathbf{a}}\), son

\ [\ begin {alineado}
-f_ {\ mathrm {k}} &=m a_ {x}\\
n-M g &=m a_ {y}
\ end {alineado}\ nonumber\]

El objeto no se mueve en la dirección\(a_{y}=0\) y; y así a partir de la segunda expresión en (8.6.19),\(N=m g\) La magnitud de la fuerza de fricción es entonces\(f_{\mathrm{k}}=\mu_{\mathrm{k}} N=\mu_{\mathrm{k}} m g\), y la primera expresión en (8.6.19) da la x -componente de aceleración como\(a_{x}=-\mu_{\mathrm{k}} g\) Becasue la aceleración es constante la x - componente de la velocidad viene dada por

\[v_{x}(t)=v_{0}+a_{x} t \nonumber \]

donde\(v_{0}\) está el componente x de la velocidad del objeto cuando acaba de comenzar a deslizarse. El desplazamiento viene dado por

\[x(t)-x_{0}=v_{0} t+\frac{1}{2} a_{x} t^{2} \nonumber \]

Denote el momento en que el bloque acaba de salir del aterrizaje\(t_{1}\), dónde\(x\left(t_{1}\right)=s\) y la velocidad justo cuando llega al rellano\(v_{x}\left(t_{1}\right)=v_{x, 1}\). La velocidad inicial es\(v_{0}\) y\(x_{0}=0\). Usando las condiciones inicial y final, y el valor de la aceleración, la ecuación (8.6.21) se convierte en

\[s=v_{0} t_{1}-\frac{1}{2} \mu_{k} g t_{1}^{2} \nonumber \]

Resolver Ecuación (8.6.20) para el momento en que el bloque llegue al borde del rellano,

\[t_{1}=\frac{v_{x, 1}-v_{0}}{-\mu_{\mathrm{k}} g}=\frac{v_{0}-v_{x, 1}}{\mu_{\mathrm{k}} g} \nonumber \]

Sustituyendo la ecuación (8.6.23) en la ecuación (8.6.22) rinde

\[s=v_{0}\left(\frac{v_{0}-v_{x, 1}}{\mu_{\mathrm{k}} g}\right)-\frac{1}{2} \mu_{k} g\left(\frac{v_{0}-v_{x, 1}}{\mu_{\mathrm{k}} g}\right)^{2} \nonumber \]

y después de algún álgebra, podemos reescribir la Ecuación (8.6.24) como

\[s=\frac{v_{0}^{2}-v_{x, 1}^{2}}{2 \mu_{\mathrm{k}} g} \nonumber \]

Desde lo alto de la escalera hasta el otro extremo de la tercera escalera, el objeto está en caída libre. Elija la\(\hat{\mathbf{i}}\) dirección positiva para que sea horizontal, dirigida a la izquierda en la Figura 8.35, y la\(\hat{\mathbf{j}}\) dirección positiva para que sea vertical (arriba) y ahora elija el origen en la parte superior de las escaleras, donde el objeto primero entra en caída libre. Los componentes de la aceleración son\(a_{x}=0\)\(a_{y}=-g\),, el componente x inicial de la velocidad es\(v_{x, 1}\), el componente y inicial de la velocidad es\(v_{y, 0}=0\), la posición x inicial es\(x_{0}=0\) y la posición y inicial es\(y_{0}=0\). Restablecer\(t=0\) cuando el objeto acaba de salir del rellano. Dejar\(t_{2}\) denotar el instante en que el objeto golpea la escalera, donde\(y\left(t_{2}\right)=-3 h\) y\(x\left(t_{2}\right)=3 d\). Las ecuaciones que describen la posición del objeto y la velocidad en el momento\(t=t_{2}\) son

\[x\left(t_{2}\right)=3 d=v_{x, 1} t_{2} \nonumber \]

\[y\left(t_{2}\right)=-3 h=-\frac{1}{2} g t_{2}^{2} \nonumber \]

Resolver Ecuación (8.6.26)\(t_{2}\) para ceder

\[t_{2}=\frac{3 d}{v_{x, 1}} \nonumber \]

Sustituir la ecuación (8.6.28) en la ecuación (8.6.27) y eliminar la variable\(t_{2}\)

\[3 h=\frac{1}{2} g \frac{9 d^{2}}{v_{x, 1}^{2}} \nonumber \]

La ecuación (8.6.29) ahora se puede resolver para el cuadrado de la componente horizontal de la velocidad,

\[v_{x, 1}^{2}=\frac{3 g d^{2}}{2 h} \nonumber \]

Ahora sustituya la Ecuación (8.6.30) por la Ecuación (8.6.25) para determinar la distancia que recorrió el objeto en el rellano,

\[s=\frac{v_{0}^{2}-\left(3 g d^{2} / 2 h\right)}{2 \mu_{\mathrm{k}} g} \nonumber \]

Ejemplo 8.8 Carrito moviéndose en una pista

Figura 8.36 Un bloque que cae acelerará un carro sobre una pista a través de la fuerza de tracción de la cuerda. El sensor de fuerza mide la tensión en la cuerda.

Considera un carro que es libre para deslizarse a lo largo de una pista horizontal (Figura 8.36). Se aplica una fuerza al carro a través de una cuerda que se une a un sensor de fuerza montado en el carro, se envuelve alrededor de una polea y se une a un bloque en el otro extremo. Cuando se suelte el bloque el carro comenzará a acelerarse. El sensor de fuerza y el carro juntos tienen una masa\(m_{\mathrm{C}}\), y el bloque suspendido tiene masa\(m_{\mathrm{B}}\). Descuidar la pequeña masa de la cuerda y la polea, y asumir que la cuerda es inextensible. El coeficiente de fricción cinética entre el carro y la pista es\(\mu_{\mathrm{k}}\). Determinar (i) la aceleración del carro, y (ii) la tensión en la cuerda.

Solución: En general, nos gustaría dibujar diagramas de cuerpo libre en todos los objetos individuales (carro, sensor, polea, cuerda y bloque) pero también podemos elegir un sistema que consta de dos (o más) objetos sabiendo que las fuerzas de interacción entre dos objetos cualesquiera se cancelarán en pares por la Tercera Ley de Newton. En este ejemplo, elegiremos el sensor/carro como un cuerpo libre, y el bloque como el otro cuerpo libre. El diagrama de fuerza de cuerpo libre para el sensor/carro se muestra en la Figura 8.37.

Figura 8.37 Diagrama de fuerza en sensor/carro con descomposición vectorial de la fuerza de contacto en componentes horizontales y verticales

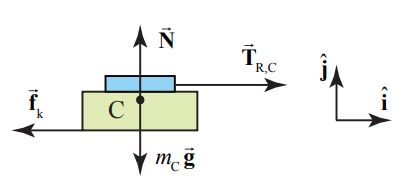
Hay tres fuerzas que actúan sobre el sensor/carro: la fuerza gravitacional\(m_{\mathrm{C}} \overrightarrow{\mathbf{g}}\), la fuerza\(\overrightarrow{\mathbf{T}}_{\mathrm{R}, \mathrm{C}}\) de tracción de la cuerda sobre el sensor de fuerza y la fuerza de contacto entre la pista y el carro. En la Figura 8.34, descomponemos la fuerza de contacto en sus dos componentes, la fuerza de fricción cinética\(\overrightarrow{\mathbf{f}}_{\mathrm{k}}=-f_{\mathrm{k}} \hat{\mathbf{i}}\) y la fuerza normal,\(\overrightarrow{\mathbf{N}}=N \hat{\mathbf{j}}\).

El carro sólo está acelerando en la dirección horizontal con\(\overrightarrow{\mathbf{a}}_{\mathrm{C}}=a_{\mathrm{C} x} \hat{\mathbf{i}}\) lo que el componente de la fuerza en la dirección vertical debe ser cero,\(a_{\mathrm{C}_{y}}=0\). Ahora podemos aplicar la Segunda Ley de Newton en las direcciones horizontal y vertical y encontrar que

\[\hat{\mathbf{i}}: T_{\mathrm{R}, \mathrm{C}}-f_{\mathrm{k}}=m_{\mathrm{C}} a_{\mathrm{C}, x} \nonumber \]

\[\hat{\mathbf{j}}: \quad N-m_{\mathrm{C}} g=0 \nonumber \]

De la Ecuación (8.6.33), concluimos que el componente normal es

\[N=m_{\mathrm{C}} g \nonumber \]

Utilizamos la Ecuación (8.6.34) para la fuerza normal para encontrar que la magnitud de la fuerza de fricción cinética es

\[f_{\mathrm{k}}=\mu_{\mathrm{k}} N=\mu_{\mathrm{k}} m_{\mathrm{c}} g \nonumber \]

Entonces la Ecuación (8.6.32) se convierte

\[T_{\mathrm{R}, \mathrm{C}}-\mu_{\mathrm{k}} m_{\mathrm{C}} g=m_{\mathrm{C}} a_{\mathrm{C}, x} \nonumber \]

El diagrama de fuerza para el bloque se muestra en la Figura 8.38. Las dos fuerzas que actúan sobre el bloque son la fuerza\(\overrightarrow{\mathbf{T}}_{\mathrm{R}, \mathrm{B}}\) de tracción de la cuerda y la fuerza gravitacional\(m_{\mathrm{B}} \overrightarrow{\mathbf{g}}\). Ahora aplicamos la Segunda Ley de Newton al bloque y encontramos que

\[\hat{\mathbf{J}}_{\mathrm{B}}: m_{\mathrm{B}} g-T_{\mathrm{R}, \mathrm{B}}=m_{\mathrm{B}} a_{B, y} \nonumber \]

Figura 8.38 Fuerzas que actúan sobre el bloque

En la Ecuación (8.6.37), el símbolo\(a_{B, y}\) representa el componente de la aceleración con signo determinado por nuestra elección de dirección descendente para el vector unitario\(\hat{\mathbf{j}}_{\mathrm{B}}\). Tenga en cuenta que hicimos una elección diferente de dirección para el vector unitario en la dirección vertical en el diagrama de cuerpo libre para el bloque que se muestra en la Figura 8.37. Cada diagrama de cuerpo libre tiene un conjunto independiente de vectores unitarios que definen una convención de signos para la descomposición vectorial de las fuerzas que actúan sobre el cuerpo libre y la aceleración del cuerpo libre. En nuestro ejemplo, con el vector unitario apuntando hacia abajo en la Figura 8.38, si resolvemos para el componente de la aceleración y es positivo, entonces sabemos que la dirección de la aceleración es hacia abajo.

Hay una segunda forma sutil de introducir signos con respecto a las fuerzas que actúan sobre un cuerpo libre. En nuestro ejemplo, la fuerza entre la cuerda y el bloque que actúa sobre el bloque apunta hacia arriba, por lo que en la descomposición vectorial de las fuerzas que actúan sobre el bloque que aparece en el lado izquierdo de la Ecuación (8.6.37), esta fuerza tiene un signo menos y la cantidad\(\overrightarrow{\mathbf{T}}_{\mathrm{R}, \mathrm{B}}=-T_{\mathrm{R}, \mathrm{B}} \hat{\mathbf{j}}_{\mathrm{B}}\) donde\(T_{\mathrm{R}, \mathrm{B}}\) se asume positiva.

Nuestra suposición de que la masa de la cuerda y la masa de la polea son insignificantes nos permite afirmar que la tensión en la cuerda es uniforme e igual en magnitud a las fuerzas en cada extremo de la cuerda,

\[T_{\mathrm{R}, \mathrm{B}}=T_{\mathrm{R}, \mathrm{C}} \equiv T \nonumber \]

También asumimos que la cadena es inextensible (no se estira). Esto implica que la cuerda, el bloque y el sensor/carro tienen la misma magnitud de aceleración,

\[a_{\mathrm{C}, x}=a_{\mathrm{B}, y} \equiv a \nonumber \]

Usando las Ecuaciones (8.6.38) y (8.6.39), ahora podemos reescribir la ecuación de movimiento para el sensor/carro, Ecuación (8.6.36), como

\[T-\mu_{\mathrm{k}} m_{\mathrm{C}} g=m_{\mathrm{C}} a \nonumber \]

y la ecuación de movimiento (8.6.37) para el bloque como

\[m_{\mathrm{B}} g-T=m_{\mathrm{B}} a \nonumber \]

Tenemos sólo dos incógnitas T y a, por lo que ahora podemos resolver las dos ecuaciones (8.6.40) y (8.6.41) simultáneamente para la aceleración del sensor/carro y la tensión en la cuerda. Primero resolvemos la Ecuación (8.6.40) para la tensión

\[T=\mu_{\mathrm{k}} m_{\mathrm{C}} g+m_{\mathrm{C}} a \nonumber \]

y luego sustituir la Ecuación (8.6.42) en la Ecuación (8.6.41) y encontrar que

\[m_{\mathrm{B}} g-\left(\mu_{\mathrm{k}} m_{\mathrm{C}} g+m_{\mathrm{C}} a\right)=m_{\mathrm{B}} a \nonumber \]

Ahora podemos resolver la Ecuación (8.6.43) para la aceleración,

\[a=\frac{m_{\mathrm{B}} g-\mu_{\mathrm{k}} m_{\mathrm{C}} g}{m_{\mathrm{C}}+m_{\mathrm{B}}} \nonumber \]

La sustitución de la Ecuación (8.6.44) en la Ecuación (8.6.42) da la tensión en la cuerda,

\ [\ begin {alineado}
T &=\ mu_ {\ mathrm {k}} m_ {\ mathrm {C}} g+m_ {\ mathrm {C}} a\\
&=\ mu_ {\ mathrm {k}} m_ {\ mathrm {C}} g+m_ {\ mathrm {C}}\ frac {m_ {\ mathrm {B}} g-\ mu_ {\ mathrm {k}} m_ {\ mathrm {C}} g} {m_ {\ mathrm {C}} +m_ {\ mathrm {B}}}\\
&=\ izquierda (\ mu_ {\ mathrm {k}} +1\ derecha)\ frac {m_ {\ mathrm {C}} m_ {\ mathrm {B}}} {m_ {\ mathrm {C}} +m_ {\ mathrm {B}}} g
\ end {alineado}\ nonumber\]

En este ejemplo, aplicamos la Segunda Ley de Newton a dos objetos, uno un objeto compuesto que consiste en el sensor y el carro, y el otro el bloque. Analizamos las fuerzas que actúan sobre cada objeto y también las restricciones impuestas a la aceleración de cada objeto. Se utilizaron las leyes de fuerza para la fricción cinética y la gravitación en cada sistema de cuerpo libre. Las tres ecuaciones de movimiento nos permiten determinar las fuerzas que dependen de los parámetros del ejemplo: la tensión en la cuerda, la aceleración de los objetos y la fuerza normal entre el carro y la mesa.

Ejemplo 8.9 Condiciones de restricción de poleas y cuerdas

Considera la disposición de poleas y bloques que se muestra en la Figura 8.39. Las poleas se suponen sin masa y sin fricción y las cuerdas de conexión son sin masa e inextensibles. Denotar las masas respectivas de los bloques como\(m_{1}\),\(m_{2}\), y\(m_{3}\). La polea superior en la figura es libre de girar pero su centro de masa no se mueve. Ambas poleas tienen el mismo radio R. a) ¿Cómo se relacionan las aceleraciones de los objetos? (b) Dibujar diagramas de fuerza en cada objeto en movimiento. c) Resolver las aceleraciones de los objetos y las tensiones en las cuerdas.

Figura 8.39 Sistema de poleas restringidas

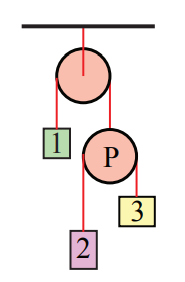
Solución: a) Elija un origen en el centro de la polea superior. Introducir funciones de coordenadas para los tres bloques móviles,\(y_{1}\),\(y_{2}\), y\(y_{3}\). Introducir una función de coordenadas\ begin {ecuación} y_ {P}\ end {ecuación} para la polea móvil (la polea en la parte inferior derecha en la Figura 8.40). Elija hacia abajo para la dirección positiva; el sistema de coordenadas se muestra en la siguiente figura entonces.

Figura 8.40 Sistema coordinado para sistema de poleas

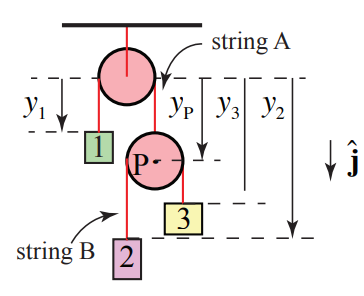
La longitud de la cadena A viene dada por

\[l_{A}=y_{1}+y_{P}+\pi R \nonumber \]

donde\(\pi R\) está la longitud del arco de la cuerda que está en contacto con la polea. Esta longitud es constante, por lo que la segunda derivada con respecto al tiempo es cero,

\[0=\frac{d^{2} l_{A}}{d t^{2}}=\frac{d^{2} y_{1}}{d t^{2}}+\frac{d^{2} y_{P}}{d t^{2}}=a_{y, 1}+a_{y, P} \nonumber \]

Así, el bloque 1 y los componentes de aceleración de la polea móvil son iguales en magnitud pero opuestos en signo,

\[a_{y, P}=-a_{y, 1} \nonumber \]

La longitud de la cadena B viene dada por

\[l_{B}=\left(y_{3}-y_{p}\right)+\left(y_{2}-y_{p}\right)+\pi R=y_{3}+y_{2}-2 y_{P}+\pi R \nonumber \]

donde\(\pi R\) está la longitud del arco de la cuerda que está en contacto con la polea. Esta longitud también es constante por lo que la segunda derivada con respecto al tiempo es cero,

\[0=\frac{d^{2} l_{B}}{d t^{2}}=\frac{d^{2} y_{2}}{d t^{2}}+\frac{d^{2} y_{3}}{d t^{2}}-2 \frac{d^{2} y_{p}}{d t^{2}}=a_{y, 2}+a_{y, 3}-2 a_{y, P} \nonumber \]

Podemos sustituir la ecuación (8.6.48) por la aceleración de la polea en la ecuación (8.6.50) produciendo la relación de restricción entre los componentes de la aceleración de los tres bloques,

\[0=a_{y, 2}+a_{y, 3}+2 a_{y, 1} \nonumber \]

b) Diagramas de fuerza de cuerpo libre: las fuerzas que actúan sobre el bloque 1 son: la fuerza gravitacional\(m_{1} \overrightarrow{\mathbf{g}}\) y la fuerza\(\overrightarrow{\mathbf{T}}_{A, 1}\) de tracción de la cuerda A que actúa sobre el bloque 1. Denote la magnitud de esta fuerza por\(T_{A}\) Debido a que se supone que la cuerda es sin masa y se supone que la polea es sin masa y sin fricción, la tensión\(T_{A}\) en la cuerda es uniforme e igual en magnitud a la fuerza de tracción de la cuerda en el bloque. El diagrama de cuerpo libre del bloque 1 se muestra en la Figura 8.41 (a).

Figura 8.41 Diagrama de fuerza de cuerpo libre en (a) bloque 1; (b) bloque 2; (c) bloque 3; (d) polea

La Segunda Ley de Newton aplicada al bloque 1 es entonces

\[\hat{\mathbf{j}}: m_{1} g-T_{A}=m_{1} a_{y, 1} \nonumber \]

Las fuerzas sobre el bloque 2 son la fuerza gravitacional\(m_{2} \overrightarrow{\mathbf{g}}\) y la cuerda B que sostiene el bloque,\(\overrightarrow{\mathbf{T}}_{B, 2}\), con magnitud\(T_{B}\). El diagrama de cuerpo libre para las fuerzas que actúan sobre el bloque 2 se muestra en la Figura 8.41 (b). La segunda Ley de Newton aplicada al bloque 2 es

\[\hat{\mathbf{j}}: m_{2} g-T_{B}=m_{2} a_{y, 2} \nonumber \]

Las fuerzas sobre el bloque 3 son la fuerza gravitacional\(m_{3} \overrightarrow{\mathbf{g}}\) y la cuerda que sostiene el bloque\(\overrightarrow{\mathbf{T}}_{B, 3}\), con magnitud igual a\(T_{B}\) porque se ha asumido que la polea P es tanto sin fricción como sin masa. El diagrama de cuerpo libre para las fuerzas que actúan sobre el bloque 3 se muestra en la Figura 8.41 (c). La segunda Ley de Newton aplicada al bloque 3 es

\[\hat{\mathbf{j}}: m_{3} g-T_{B}=m_{3} a_{y, 3} \nonumber \]

Las fuerzas sobre la polea móvil P son la fuerza gravitacional\(m_{P} \overrightarrow{\mathbf{g}}=\overrightarrow{\mathbf{0}}\) (la polea se asume sin masa); la cuerda B tira hacia abajo de la polea en cada lado con una fuerza,\(\overrightarrow{\mathbf{T}}_{B, P}\) que tiene magnitud\(T_{B}\). La cuerda A sostiene la polea con una fuerza\(\overrightarrow{\mathbf{T}}_{A, P}\) con la magnitud\(T_{A}\) igual a la tensión en la cuerda A. El diagrama de cuerpo libre para las fuerzas que actúan sobre la polea móvil se muestra en la Figura 8.41 (d). La segunda Ley de Newton aplicada a la polea es

\[\hat{\mathbf{j}}: 2 T_{B}-T_{A}=m_{P} a_{y, P}=0 \nonumber \]

Debido a que se supone que la polea es sin masa, podemos usar esta última ecuación para determinar la condición que debe satisfacer la tensión en las dos cuerdas,

\[2 T_{B}=T_{A} \nonumber \]

Ahora estamos en posición de determinar las aceleraciones de los bloques y la tensión en las dos cuerdas. Registramos las ecuaciones relevantes como resumen.

\[0=a_{y, 2}+a_{y, 3}+2 a_{y, 1} \nonumber \]

\[m_{1} g-T_{A}=m_{1} a_{y, 1} \nonumber \]

\[m_{2} g-T_{B}=m_{2} a_{y, 2} \nonumber \]

\[m_{3} g-T_{B}=m_{3} a_{y, 3} \nonumber \]

\[2 T_{B}=T_{A} \nonumber \]

Hay cinco ecuaciones con cinco incógnitas, así podemos resolver este sistema. Primero usaremos la Ecuación (8.6.61) para eliminar la tensión\(T_{A}\) en la Ecuación (8.6.58), cediendo

\[m_{1} g-2 T_{B}=m_{1} a_{y, 1} \nonumber \]

Ahora resolvemos las Ecuaciones (8.6.59), (8.6.60) y (8.6.62) para las aceleraciones,

\[a_{y, 2}=g-\frac{T_{B}}{m_{2}} \nonumber \]

\[a_{y, 3}=g-\frac{T_{B}}{m_{3}} \nonumber \]

\[a_{y, 1}=g-\frac{2 T_{B}}{m_{1}} \nonumber \]

Ahora sustituimos estos resultados por las aceleraciones en la ecuación de restricción, Ecuación (8.6.57),

\[0=g-\frac{T_{B}}{m_{2}}+g-\frac{T_{B}}{m_{3}}+2 g-\frac{4 T_{B}}{m_{1}}=4 g-T_{B}\left(\frac{1}{m_{2}}+\frac{1}{m_{3}}+\frac{4}{m_{1}}\right) \nonumber \]

Ahora podemos resolver esta última ecuación para la tensión en la cuerda B,

\[T_{B}=\frac{4 g}{\left(\frac{1}{m_{2}}+\frac{1}{m_{3}}+\frac{4}{m_{1}}\right)}=\frac{4 g m_{1} m_{2} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}} \nonumber \]

De la Ecuación (8.6.61), la tensión en la cuerda A es

\[T_{A}=2 T_{B}=\frac{8 g m_{1} m_{2} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}} \nonumber \]

Encontramos la aceleración del bloque 1 de la Ecuación (8.6.65), usando la Ecuación (8.6.67) para la tensión en la cuerda B,

\[a_{y, 1}=g-\frac{2 T_{B}}{m_{1}}=g-\frac{8 g m_{2} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}}=g \frac{m_{1} m_{3}+m_{1} m_{2}-4 m_{2} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}} \nonumber \]

Encontramos la aceleración del bloque 2 de la Ecuación (8.6.63), usando la Ecuación (8.6.67) para la tensión en la cuerda B,

\[a_{y, 2}=g-\frac{T_{B}}{m_{2}}=g-\frac{4 g m_{1} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}}=g \frac{-3 m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}} \nonumber \]

De igual manera, encontramos la aceleración del bloque 3 de la Ecuación (8.6.64), usando la Ecuación (8.6.67) para la tensión en la cuerda B,

\[a_{y, 3}=g-\frac{T_{B}}{m_{3}}=g-\frac{4 g m_{1} m_{2}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}}=g \frac{m_{1} m_{3}-3 m_{1} m_{2}+4 m_{2} m_{3}}{m_{1} m_{3}+m_{1} m_{2}+4 m_{2} m_{3}} \nonumber \]

Como comprobación de nuestro álgebra observamos que

\ [\ begin {array} {l}
2 a_ {1, y} +a_ {2, y} +a_ {3, y} =\\
2 g\ frac {m_ {1} m_ {3} +m_ {1} m_ {2} -4 m_ {2} m_ {3}} {m_ {1} m_ {3} +m_ {1} _ {2} +4 m_ {2} m_ {3}} +g\ frac {-3 m_ {1} m_ {3} +m_ {1} m_ {2} +4 m_ {2} m_ {3}} {m_ {1} m_ {3} +m_ {1} m_ {2} +4 m_ {2} m_ {3}} +g\ frac ac {m_ {1} m_ {3} -3 m_ {1} m_ {2} +4 m_ {2} m_ {3}} {m_ {1} m_ {3} +m_ {1} m_ {2} +4 m_ {2} m_ {3}}\\
=0
\ end {array}\ nonumber\]

Ejemplo 8.10 Cuña aceleradora

Figura 8.42 Bloque en cuña de aceleración

Una cuña de 45o es empujada a lo largo de una mesa con aceleración constante\(\overrightarrow{\mathbf{A}}\) según un observador en reposo con respecto a la mesa. Un bloque de masa m se desliza sin fricción por la cuña (Figura 8.42). Encuentra su aceleración con respecto a un observador en reposo con respecto a la mesa. Anote un plan para encontrar la magnitud de la aceleración del bloque. Asegúrese de indicar claramente qué conceptos planea usar para calcular cualquier cantidad física relevante. También indique claramente cualquier suposición que haga. Asegúrese de incluir cualquier diagrama de fuerza de cuerpo libre o bocetos que planea usar.

Solución: Elija un sistema de coordenadas para el bloque y la cuña como se muestra en la Figura 8.43. Entonces\(\overrightarrow{\mathbf{A}}=A_{x, w} \hat{\mathbf{i}}\) donde\(A_{x, w}\) está el componente x de la aceleración de la cuña.

Figura 8.43 Sistema de coordenadas para bloque en cuña de aceleración

Aplicaremos la Segunda Ley de Newton al bloque que se desliza por la cuña. Debido a que la cuña se está acelerando, existe una relación de restricción entre los componentes x - e y - de la aceleración del bloque. Para encontrar esa restricción elegimos un sistema de coordenadas para la cuña y el bloque que se desliza hacia abajo de la cuña que se muestra en la siguiente figura. Encontraremos la relación de restricción entre los componentes de las aceleraciones del bloque y la cuña mediante un argumento geométrico. De la figura anterior, vemos que

\[\tan \phi=\frac{y_{b}}{l-\left(x_{b}-x_{w}\right)} \nonumber \]

Por lo tanto

\[y_{b}=\left(l-\left(x_{b}-x_{w}\right)\right) \tan \phi \nonumber \]

Si diferenciamos la Ecuación (8.6.73) dos veces con respecto al tiempo señalando que

\[\frac{d^{2} l}{d t^{2}}=0 \nonumber \]

tenemos eso

\[\frac{d^{2} y_{b}}{d t^{2}}=-\left(\frac{d^{2} x_{b}}{d t^{2}}-\frac{d^{2} x_{w}}{d t^{2}}\right) \tan \phi \nonumber \]

Por lo tanto

\[a_{b, y}=-\left(a_{b, x}-A_{x, w}\right) \tan \phi \nonumber \]

donde

\[A_{x, w}=\frac{d^{2} x_{w}}{d t^{2}} \nonumber \]

Ahora dibujamos un diagrama de fuerza de cuerpo libre para el bloque (Figura 8.44). La Segunda Ley de Newton en la\(\hat{\mathbf{i}}\) dirección se convierte

\[N \sin \phi=m a_{b x} \nonumber \]

y la\(\hat{\mathbf{j}}\) dirección se convierte en

\[N \cos \phi-m g=m a_{b, y} \nonumber \]

Figura 8.44 Diagrama de fuerza de cuerpo libre en bloque

Podemos resolver para la fuerza normal a partir de la Ecuación (8.6.78):

\[N=\frac{m a_{b, x}}{\sin \phi} \nonumber \]

Ahora sustituimos la Ecuación (8.6.76) y la Ecuación (8.6.80) en la Ecuación (8.6.79) rindiendo

\[\frac{m a_{b, x}}{\sin \phi} \cos \phi-m g=m\left(-\left(a_{b, x}-A_{w, x}\right) \tan \phi\right) \nonumber \]

Ahora limpiamos esto cediendo

\[m a_{b, x}(\operatorname{cotan} \phi+\tan \phi)=m\left(g+A_{w, x} \tan \phi\right) \nonumber \]

Por lo tanto, el componente x de la aceleración es entonces

\[a_{b, x}=\frac{g+A_{w, x} \tan \phi}{\operatorname{cotan} \phi+\tan \phi} \nonumber \]

A partir de la Ecuación (8.6.76), el componente y de la aceleración es entonces

\[a_{b, y}=-\left(a_{b, x}-A_{w, x}\right) \tan \phi=-\left(\frac{g+A_{w, x} \tan \phi}{\operatorname{cotan} \phi+\tan \phi}-A_{w, x}\right) \tan \phi \nonumber \]

Esto simplifica

\[a_{b, y}=\frac{A_{w, x}-g \tan \phi}{\operatorname{cotan} \phi+\tan \phi} \nonumber \]

Cuando\(\phi=45^{\circ}\), cotan\(45^{\circ}=\tan 45^{\circ}=1\), y así la ecuación (8.6.83) se convierte

\[a_{b, x}=\frac{g+A_{w, x}}{2} \nonumber \]

y la Ecuación (8.6.85) se convierte

\[a_{b, y}=\frac{A-g}{2} \nonumber \]

La magnitud de la aceleración es entonces

\ [\ begin {alineado}
a=\ sqrt {a_ {b, x} ^ {2} +a_ {b, y} ^ {2}} &=\ sqrt {\ izquierda (\ frac {g+a_ {w x}} {2}\ derecha) ^ {2} +\ izquierda (\ frac {A_ {w x} -g} {2}\ derecha) ^ {^ 2}}\\
a &=\ sqrt {\ left (\ frac {g^ {2} +A_ {w} ^ {2}} {2}\ derecha)}
\ end {alineado}\ nonumber\]

Ejemplo 8.11: Capstan

Un dispositivo llamado cabrestante se utiliza a bordo de barcos con el fin de controlar una cuerda que se encuentra bajo gran tensión. La cuerda se envuelve alrededor de un tambor fijo de radio R, generalmente para varias vueltas (la Figura 8.45 muestra alrededor de tres cuartos de vuelta visto desde arriba). La carga sobre la cuerda la tira con una fuerza\(T_{A}\) y el marinero sostiene el otro extremo de la cuerda con una fuerza mucho menor\(T_{B}\). El coeficiente de fricción estática entre la cuerda y el tambor es\(\mu_{\mathrm{s}}\). El marinero está sujetando la cuerda para que esté a punto de deslizarse. Demuestre que\(T_{B}=T_{A} e^{-\mu_{s} \theta_{B A}}\) dónde\(\theta_{B A}\) está el ángulo subtendido por la cuerda en el tambor.

Figura 8.47. El borde derecho de la rebanada está en el ángulo θ y el borde izquierdo de la rebanada está en\(\theta+\Delta \theta\) El extremo del borde del ángulo de la rebanada hace con la horizontal es\(\Delta \theta / 2\). Hay cuatro fuerzas que actúan sobre esta sección de la cuerda. Las fuerzas son la fuerza normal entre el cabrestante y la cuerda que apunta hacia afuera, una fuerza de fricción estática y las tensiones en cada extremo de la rebanada. La cuerda se sujeta en el punto justo de deslizamiento, por lo que si la carga ejerce una mayor fuerza la cuerda se deslizará hacia la derecha. Por lo tanto, la dirección de la fuerza de fricción estática entre el cabrestante y la cuerda, actuando sobre la cuerda, apunta hacia la izquierda. La tensión en el lado derecho de la rebanada se denota por\(T(\theta) \equiv T\), mientras que la tensión en el lado izquierdo de la rebanada se denota por\(T(\theta+\Delta \theta) \equiv T+\Delta T\). ¿La tensión en esta rebanada del lado derecho a la izquierda, aumenta, permanece igual o disminuye? La tensión disminuye debido a que la carga en el lado izquierdo es menor que la carga en el lado derecho. Tenga en cuenta que\(\Delta T<0\).

Figura 8.47 Diagrama de fuerza de cuerpo libre en una pequeña porción de cuerda

La descomposición vectorial de las fuerzas viene dada por

\[\hat{\mathbf{i}}: T \cos (\Delta \theta / 2)-f_{s}-(T+\Delta T) \cos (\Delta \theta / 2) \nonumber \]

\[\hat{\mathbf{j}}:-T \sin (\Delta \theta / 2)+N-(T+\Delta T) \sin (\Delta \theta / 2) \nonumber \]

Para ángulos pequeños\(\Delta \theta\),\(\cos (\Delta \theta / 2) \cong 1\), y\(\sin (\Delta \theta / 2) \cong \Delta \theta / 2\) Usando las aproximaciones de ángulo pequeño, la descomposición vectorial de las fuerzas en la dirección x (la\(\hat{\mathbf{i}}\) dirección) se convierte en

\ [\ comenzar {alineado}
T\ cos (\ Delta\ theta/2) -f_ {s} - (T+\ Delta T)\ cos (\ Delta\ theta/2) &\ simeq T-f_ {s} - (T+\ Delta T)\\
&=-f_ {s} -\ Delta T
\ final {alineado}\ nonumber\]

Por la condición de equilibrio estático la suma de los componentes x de las fuerzas es cero,

\[-f_{\mathrm{s}}-\Delta T=0 \nonumber \]

La descomposición vectorial de las fuerzas en la dirección y (la\(+\hat{\mathbf{j}}\) dirección -) es aproximadamente

\ [\ begin {alineado}
-T\ sin (\ Delta\ theta/2) +N- (T+\ Delta T)\ sin (\ Delta\ theta/2) &\ siMeq-T\ Delta\ theta/2+N- (T+\ Delta T)\ Delta\ theta/2\
&=-T\ Delta\ theta+n-\ Delta T\ Delta\ theta/2
\ end {alineado}\ nonumber\]

En la última ecuación anterior podemos ignorar los términos proporcionales a\(\Delta T \Delta \theta\) porque estos son producto de dos pequeñas cantidades y por lo tanto son mucho más pequeños que los términos proporcionales a cualquiera\(\Delta T\) o\(\Delta \theta\). La descomposición del vector en la dirección y se convierte en

\[-T \Delta \theta+N \nonumber \]

El equilibrio estático implica que esta suma de los componentes y de las fuerzas es cero,

\[-T \Delta \theta+N=0 \nonumber \]

Podemos resolver esta ecuación para la magnitud de la fuerza normal

\[N=T \Delta \theta \nonumber \]

La condición de deslizamiento justo es que la magnitud de la fricción estática alcanza su valor máximo

\[f_{\mathrm{s}}=\left(f_{\mathrm{s}}\right)_{\max }=\mu_{\mathrm{s}} N \nonumber \]

Ahora podemos combinar las Ecuaciones (8.6.92) y (8.6.97) para rendir

\[\Delta T=-\mu_{s} N \nonumber \]

Ahora sustituya la magnitud de la fuerza normal, Ecuación (8.6.96), por la Ecuación (8.6.98), cediendo

\[-\mu_{s} T \Delta \theta-\Delta T=0 \nonumber \]

Finalmente, resolver esta ecuación para la relación entre el cambio de tensión y el cambio de ángulo,

\[\frac{\Delta T}{\Delta \theta}=-\mu_{\mathrm{s}} T \nonumber \]

La derivada de la tensión con respecto al ángulo θ se define como el límite

\[\frac{d T}{d \theta} \equiv \lim _{\Delta \theta \rightarrow 0} \frac{\Delta T}{\Delta \theta} \nonumber \]

y la Ecuación (8.6.100) se convierte

\[\frac{d T}{d \theta}=-\mu_{s} T \nonumber \]

Este es un ejemplo de una ecuación diferencial lineal de primer orden que muestra que la tasa de cambio de tensión con respecto al ángulo θ es proporcional al negativo de la tensión en ese ángulo θ. Esta ecuación se puede resolver mediante la integración utilizando la técnica de separación de variables. Primero reescribimos la ecuación (8.6.102) como

\[\frac{d T}{T}=-\mu_{s} d \theta \nonumber \]

Integrar ambos lados, señalando que cuando θ = 0, la tensión es igual a la fuerza de la carga\(T_{A}\) y cuando ángulo\(\theta=\theta_{A, B}\) la tensión es igual a la fuerza que\(T_{B}\) el marinero aplica a la cuerda,

\[\int_{T=T_{A}}^{T=T_{B}} \frac{d T}{T}=-\int_{\theta=0}^{\theta=\theta_{B A}} \mu_{s} d \theta \nonumber \]

El resultado de la integración es

\[\ln \left(\frac{T_{B}}{T_{A}}\right)=-\mu_{s} \theta_{B A} \nonumber \]

Tenga en cuenta que el exponencial del logaritmo natural

\[\exp \left(\ln \left(\frac{T_{B}}{T_{A}}\right)\right)=\frac{T_{B}}{T_{A}} \nonumber \]

por lo que exponenciar ambos lados de la Ecuación (8.6.105) rinde

\[\frac{T_{B}}{T_{A}}=e^{-\mu_{\mathrm{s}} \theta_{B A}} \nonumber \]

la tensión disminuye exponencialmente,

\[T_{B}=T_{A} e^{-\mu_{s} \theta_{B A}} \nonumber \]

Debido a que la tensión disminuye exponencialmente, el marinero solo necesita aplicar una pequeña fuerza para evitar que la cuerda se deslice.

Ejemplo 8.12 Caída Libre con Arrastre Aéreo

Considera un objeto de masa m que está en caída libre pero que experimenta resistencia al aire. La magnitud de la fuerza de arrastre viene dada por la Ecuación (8.6.1), donde\(\rho\) está la densidad del aire, A es el área de la sección transversal del objeto en un plano perpendicular al movimiento, y\(C_{D}\) el coeficiente de arrastre. Supongamos que el objeto se libera del reposo y alcanza muy rápidamente velocidades en las que se aplica la Ecuación (8.6.1). Determinar (i) la velocidad terminal, y (ii) la velocidad del objeto en función del tiempo.

Solución: Elija dirección y positiva hacia abajo con el origen en la posición inicial del objeto como se muestra en la Figura 8.48 (a).

Figura 8.48 (a) Sistema de coordenadas para mármol; (b) diagrama de fuerza corporal libre sobre mármol

Hay dos fuerzas que actúan sobre el objeto: la fuerza gravitacional y la fuerza de arrastre que viene dada por la Ecuación (8.6.1). El diagrama de cuerpo libre se muestra en la Figura 8.48 (b). La Segunda Ley de Newton es entonces

\[m g-(1 / 2) C_{D} A \rho v^{2}=m \frac{d v}{d t} \nonumber \]

Set\(\beta=(1 / 2) C_{D} A \rho\). La Segunda Ley de Newton puede escribirse como

\[m g-\beta v^{2}=m \frac{d v}{d t} \nonumber \]

Inicialmente cuando el objeto se acaba de liberar con v = 0, el arrastre de aire es cero y la aceleración dv/dt es máxima. A medida que el objeto aumenta su velocidad, el arrastre de aire se hace más grande y dv/dt disminuye hasta que el objeto alcanza la velocidad terminal y dv/dt = 0. Establecer dv/dt = 0 en la Ecuación (8.6.15) y resolver para el rendimiento de velocidad terminal.

\[v_{\infty}=\sqrt{\frac{m g}{\beta}}=\sqrt{\frac{2 m g}{C_{D} A \rho}} \nonumber \]

Los valores para la magnitud de la velocidad terminal se muestran en la Tabla 8.3 para una variedad de objetos con el mismo coeficiente de arrastre\(C_{D}=0.5\)

Tabla 8.3 Velocidades terminales para objetos de diferentes tamaños con\(C_{D}=0.5\)

Para integrar la Ecuación (8.6.15), aplicaremos la técnica de separación de variables e integración por fracciones parciales. Primera ecuación de reescritura (8.6.15) como

\[\frac{-\beta}{m} d t=\frac{d v}{\left(v^{2}-\frac{m g}{\beta}\right)}=\frac{d v}{\left(v^{2}-v_{\infty}^{2}\right)}=\left(-\frac{1}{2 v_{\infty}\left(v+v_{\infty}\right)}+\frac{1}{2 v_{\infty}\left(v-v_{\infty}\right)}\right) d v \nonumber \]

Una expresión integral de la Ecuación (8.6.112) es entonces

\[-\int_{v^{\prime}=0}^{v^{\prime}=v(t)} \frac{d v^{\prime}}{2 v_{\infty}\left(v^{\prime}+v_{\infty}\right)}+\int_{v=0}^{v=v(t)} \frac{d v^{\prime}}{2 v_{\infty}\left(v^{\prime}-v_{\infty}\right)}=-\frac{\beta}{m} \int_{t=0}^{t^{\prime}=t} d t^{\prime} \nonumber \]

Rendimientos de integración

\ [\ begin {array} {l}
-\ int_ {v^ {\ prime} =0} ^ {v^ {\ prime} =v (t)}\ frac {d v^ {\ prime}} {2 v_ {\ infty}\ left (v^ {\ prime} +v_ {\ infty}\ derecha)} +\ int_ {v^ {\ prime} =0} ^ {v^ {\ prime} =v (t)}\ frac {d v^ {\ prime}} {2 v_ {\ infty}\ left (v^ {\ prime} -v_ {\ infty}\ derecha)} =-\ frac {\ beta^ {t^ {\ prime} =t}} {m}\ int_ {t^ {\ prime} =0} {t} d t^ {\ prime }\\
\ frac {1} {2 v_ {\ infty}}\ izquierda (-\ ln\ izquierda (\ frac {v (t) +v_ {\ infty}} {v_ {\ infty}}\ derecha) +\ ln\ izquierda (\ frac {v_ {\ infty} -v (t)} {v_ {\ infty}}\ infty}\ derecha) derecha\) =-\ frac {\ beta} {m} t
\ end {array}\ nonumber\]

Después de algunas manipulaciones algebraicas, la ecuación (8.6.114) se puede reescribir como

\[\ln \left(\frac{v_{\infty}-v(t)}{v(t)+v_{\infty}}\right)=-\frac{2 v_{\infty} \beta}{m} t \nonumber \]

Ecuación exponenciada (8.6.115) rendimientos

\[\left(\frac{v_{\infty}-v(t)}{v(t)+v_{\infty}}\right)=e^{-\frac{2 v_{\omega} \beta}{m} t} \nonumber \]

Después de algún reordenamiento algebraico, la componente y de la velocidad en función del tiempo viene dada por

\ [\ begin {array} {c}
v (t) =v_ {\ infty}\ izquierda (\ frac {1-e^ {-\ frac {2 v_ {w}\ beta_ {t}} {m}} {1+e^ {-\ frac {2 v_ {\ infty}\ beta_ {t}} {m}}\ derecha) =v_ {\ infty}\ tan h\ izquierda (\ frac {v_ {\ infty}\ beta} {m} t\ derecha)\
\ texto {donde}\ frac {v_ {\ infty}\ beta} {m} =\ frac {\ beta} {m}\ sqrt {\ frac {m g} {\ beta}} =\ sqrt {\ frac {\ beta g} {m}} =\ sqrt {\ frac {(1/2) C_ {D} A\ rho g} {m}}
\ end {array}\ nonumber\]