10.9: Ejemplos trabajados

Estrategias de resolución de problemas

Al resolver problemas que impliquen un cambio de impulso en un sistema, emplearemos nuestra estrategia general de resolución de problemas que implica cuatro pasos básicos:

1. Entender — obtener una comprensión conceptual del problema.

2. Diseñar un Plan - establecer un procedimiento para obtener la solución deseada.

3. Lleva nuestro plan — ¡resuelve el problema!

4. Mirar hacia atrás: verifique su solución y método de solución.

Desarrollaremos un conjunto de ideas orientadoras para los dos primeros pasos.

1. Entender — obtener una comprensión conceptual del problema

La primera pregunta que debes hacer es si el impulso es constante o no en algún sistema que está cambiando su estado después de sufrir una interacción. Primero debes identificar los objetos que componen el sistema y cómo están cambiando su estado debido a la interacción. Como guía, tratar de determinar qué objetos cambian su impulso en el curso de la interacción. Debes realizar un seguimiento del impulso de estos objetos antes y después de cualquier interacción. En segundo lugar, el impulso es una cantidad vectorial por lo que la cuestión de si el impulso es constante o no debe responderse en cada dirección relevante. Para determinar esto, existen dos consideraciones importantes. Debe identificar cualquier fuerza externa que actúe sobre el sistema. Recuerde que una fuerza externa distinta de cero hará que el impulso del sistema cambie, (Ecuación (10.4.9) anterior),

\[\overrightarrow{\mathbf{F}}^{e x t}=\frac{d \overrightarrow{\mathbf{p}}_{\mathrm{sys}}}{d t} \nonumber \]

La ecuación (10.9.1) es una ecuación vectorial; si la fuerza externa en alguna dirección es cero, entonces el cambio de impulso en esa dirección es cero. En algunos casos, las fuerzas externas pueden actuar pero el intervalo de tiempo durante el cual se produce la interacción es tan pequeño que el impulso es pequeño en magnitud en comparación con el impulso y podría ser insignificante. Recordemos que el impulso externo promedio cambia el impulso del sistema

\[\overrightarrow{\mathbf{I}}=\overrightarrow{\mathbf{F}}^{\mathrm{ext}} \Delta t_{\mathrm{int}}=\Delta \overrightarrow{\mathbf{p}}_{\mathrm{sys}} \nonumber \]

Si el tiempo de interacción es lo suficientemente pequeño, el impulso del sistema es constante,\(\Delta \overrightarrow{\mathbf{p}} \rightarrow \overrightarrow{\mathbf{0}}\) Si el impulso no es constante entonces debes aplicar ya sea la Ecuación (10.9.1) o la Ecuación (10.9.2). Si el impulso del sistema es constante, entonces se puede aplicar la Ecuación (10.7.5),

\[\overrightarrow{\mathbf{p}}_{\mathrm{sys}, i}=\overrightarrow{\mathbf{p}}_{\mathrm{sys}, f} \nonumber \]

Si no hay fuerza externa neta en alguna dirección, por ejemplo la dirección x, el componente de impulso es constante en esa dirección, y debe aplicar

\[\mathbf{p}_{\mathrm{sys}, x, i}=\mathbf{p}_{\mathrm{sys},x, f} \nonumber \]

2. Diseñar un Plan - establecer un procedimiento para obtener la solución deseada

Dibuja diagramas de todos los elementos de tu sistema para los dos estados inmediatamente antes y después de que el sistema cambie su estado. Elija símbolos para identificar cada masa y velocidad en el sistema. Identificar un conjunto de direcciones positivas y vectores unitarios para cada estado. Elija sus símbolos para corresponder al estado y movimiento (esto facilita una interpretación fácil, por ejemplo\(\left(v_{x, i}\right)_{1}\) representa el componente x de la velocidad del objeto 1 en el estado inicial y\(\left(v_{x, f}\right)_{1}\) representa el componente x de la velocidad del objeto 1 en el estado final). Decide si estás usando componentes o magnitudes para tus símbolos de velocidad. Dado que el momentum es una cantidad vectorial, identifique los componentes vectoriales inicial y final del momentum. Nos referiremos a estos diagramas como diagramas de flujo de momento. En base a su modelo, ahora puede escribir expresiones para el impulso inicial y final de su sistema. Como ejemplo en el que dos objetos se mueven solo en la dirección x, el componente x inicial del momento es

\[p_{\text {sys }, x, i}=m_{1}\left(v_{x, i}\right)_{1}+m_{2}\left(v_{x, i}\right)_{2}+\cdots \nonumber \]

El componente x final del impulso es

\[p_{\text {sys, } x, f}=m_{1}\left(v_{x, f}\right)_{1}+m_{2}\left(v_{x, f}\right)_{2}+\cdots \nonumber \]

Si el componente x del impulso es constante entonces

\[\mathbf{p}_{\mathrm{sys}, x, i}=\mathbf{p}_{\mathrm{sys},x, f} \nonumber \]

Ahora podemos sustituir las Ecuaciones (10.9.5) y (10.9.6) en la Ecuación (10.9.7), rindiendo

\[m_{1}\left(v_{x, i}\right)_{1}+m_{2}\left(v_{x, i}\right)_{2}+\cdots=m_{1}\left(v_{x, f}\right)_{1}+m_{2}\left(v_{x, f}\right)_{2}+\cdots \nonumber \]

La ecuación (10.9.8) ahora se puede utilizar para cualquier análisis adicional requerido por un problema en particular. Por ejemplo, es posible que tengas suficiente información para calcular las velocidades finales de los objetos después de la interacción. Si es así entonces lleva a cabo tu plan y revisa tu solución, especialmente dimensiones o unidades y cualquier dirección vectorial relevante.

Ejemplo 10.5 Proyectil explosivo

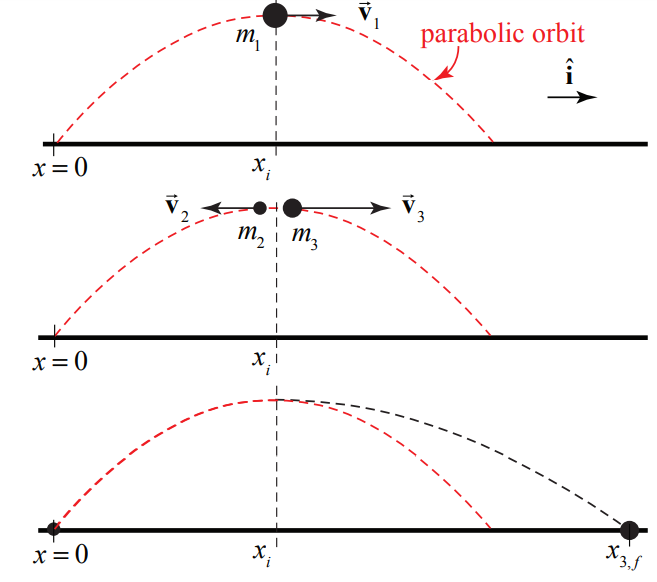
Un proyectil de masa portador de instrumentos explota\(m_{1}\) accidentalmente en la parte superior de su trayectoria. La distancia horizontal entre el punto de lanzamiento y la explosión es\(x_{i}\). El proyectil se rompe en dos pedazos que vuelan separados horizontalmente. La pieza más grande,\(m_{3}\) tiene tres veces la masa de la pieza más pequeña,\(m_{2}\). Para sorpresa del científico a cargo, la pieza más pequeña regresa a la tierra en la estación de lanzamiento. Descuidar la resistencia del aire y los efectos debidos a la curvatura de la tierra. ¿A qué distancia\(x_{3, f}\), del punto de lanzamiento original, aterriza la pieza más grande?

Figura 10.8 Trayectorias explosivas de proyectiles

Solución: Podemos resolver este problema de dos maneras diferentes. El enfoque más fácil es utilizar el hecho de que la fuerza externa es la fuerza gravitacional y por lo tanto el centro de masa del sistema sigue una trayectoria parabólica. De la información dada en el problema\(m_{2}=m_{1} / 4\) y\(m_{3}=3 m_{1} / 4\). Así, cuando los dos objetos regresan al suelo el centro de masa del sistema ha recorrido una distancia\(R_{c m}=2 x_{i}\). Ahora usamos la definición de centro de masa para encontrar donde el objeto con la mayor masa golpea el suelo. Elija un origen en el punto de partida. El centro de masa del sistema viene dado por

\[\overrightarrow{\mathbf{R}}_{c m}=\frac{m_{2} \overrightarrow{\mathbf{r}}_{2}+m_{3} \overrightarrow{\mathbf{r}}_{3}}{m_{2}+m_{3}} \nonumber \]

Entonces, cuando los objetos chocan contra el suelo\(\overrightarrow{\mathbf{R}}_{c m}=2 x_{i} \hat{\mathbf{i}}\), el objeto con la masa más pequeña regresa al origen\(\overrightarrow{\mathbf{r}}_{2}=\overrightarrow{\mathbf{0}}\), y el vector de posición del otro objeto es\(\overrightarrow{\mathbf{r}}_{3}=x_{3, f} \hat{\mathbf{i}}\). Entonces, usando la definición del centro de masa,

\[2 x_{i} \hat{\mathbf{i}}=\frac{\left(3 m_{1} / 4\right) x_{3, f} \hat{\mathbf{i}}}{m_{1} / 4+3 m_{1} / 4}=\frac{\left(3 m_{1} / 4\right) x_{3, f} \hat{\mathbf{i}}}{m_{1}}=\frac{3}{4} x_{3, f} \hat{\mathbf{i}} \nonumber \]

Por lo tanto

\[x_{3, f}=\frac{8}{3} x_{i} \nonumber \]

Nótese que ni la altura vertical sobre el suelo ni la aceleración gravitacional g entraron en nuestra solución.

Alternativamente, podemos utilizar la conservación del impulso y la cinemática para encontrar la distancia recorrida. Debido a que la pieza más pequeña regresa al punto de partida después de la colisión, la velocidad de la pieza más pequeña inmediatamente después de la explosión es igual a la negativa de la velocidad del objeto original inmediatamente antes de la explosión. Debido a que la colisión es instantánea, la componente horizontal del momento es constante durante la colisión. Podemos usar esto para determinar la velocidad de la pieza más grande después de la colisión. La pieza más grande tarda la misma cantidad de tiempo en regresar al suelo que el proyectil tarda originalmente en llegar a la cima del vuelo. Por lo tanto, podemos determinar hasta qué punto viajó horizontalmente la pieza más grande.

Comenzamos por identificar diversos estados en el problema.

Estado inicial, tiempo\(t_{0}=0\): se lanza el proyectil.

Estado 1 vez\(t_{1}\): el proyectil se encuentra en la parte superior de su trayectoria de vuelo inmediatamente antes de la explosión. La masa es\(m_{1}\) y la velocidad del proyectil es\(\overrightarrow{\mathbf{v}}_{1}=v_{1} \hat{\mathbf{i}}\).

Estado 2 tiempo\(t_{2}\): inmediatamente después de la explosión, el proyectil se ha roto en dos pedazos, uno de masa\(m_{2}\) moviéndose hacia atrás (en la dirección x negativa) con velocidad\(\overrightarrow{\mathbf{v}}_{2}=-\overrightarrow{\mathbf{v}}_{1}\). El otro trozo de masa\(m_{3}\) se mueve en la dirección x positiva con la velocidad\(\overrightarrow{\mathbf{v}}_{3}=v_{3} \hat{\mathbf{i}}\), (Figura 10.8).

Estado 3: las dos piezas golpean el suelo en el momento\(t_{f}=2 t_{1}\) una en el lugar de lanzamiento original 1 y la otra a distancia,\(x_{3, f}\) del lugar de lanzamiento, como se indica en la Figura 10.8. Las piezas tardan la misma cantidad de tiempo en llegar al suelo\(\Delta t=t_{1}\) porque ambas piezas están cayendo desde la misma altura que la pieza original alcanzada en el momento\(t_{1}\) y cada una no tiene componente de velocidad en la dirección vertical inmediatamente después de la explosión. El diagrama de flujo de impulso con el estado 1 como estado inicial y el estado 2 como estado final se muestran en los dos diagramas superiores de la Figura 10.8.

El impulso inicial en el momento\(t_{1}\) inmediatamente anterior a la explosión es

\[\overrightarrow{\mathbf{p}}^{s s}\left(t_{1}\right)=m_{1} \overrightarrow{\mathbf{v}}_{1} \nonumber \]

El impulso en el momento\(t_{2}\) inmediatamente después de la explosión es

\[\overrightarrow{\mathbf{p}}^{g s}\left(t_{2}\right)=m_{2} \overrightarrow{\mathbf{v}}_{2}+m_{3} \overrightarrow{\mathbf{v}}_{3}=-\frac{1}{4} m_{1} \overrightarrow{\mathbf{v}}_{1}+\frac{3}{4} m_{1} \overrightarrow{\mathbf{v}}_{3} \nonumber \]

Durante la duración de la explosión instantánea, se puede descuidar el impulso debido a la fuerza gravitacional externa y por lo tanto el impulso del sistema es constante. En la dirección horizontal, tenemos que

\[m_{1} \overrightarrow{\mathbf{v}}_{1}=-\frac{1}{4} m_{1} \overrightarrow{\mathbf{v}}_{1}+\frac{3}{4} m_{1} \overrightarrow{\mathbf{v}}_{3} \nonumber \]

La ecuación (10.9.11) ahora se puede resolver para la velocidad de la pieza más grande inmediatamente después de la colisión,

\[\overrightarrow{\mathbf{v}}_{3}=\frac{5}{3} \overrightarrow{\mathbf{v}}_{1} \nonumber \]

La pieza más grande recorre una distancia

\[x_{3, f}=v_{3} t_{1}=\frac{5}{3} v_{1} t_{1}=\frac{5}{3} x_{i} \nonumber \]

Por lo tanto la distancia total recorrida por la pieza más grande desde la estación de lanzamiento es

\[x_{f}=x_{i}+\frac{5}{3} x_{i}=\frac{8}{3} x_{i} \nonumber \]

de acuerdo con nuestro enfoque anterior.

Ejemplo 10.6 Plano de aterrizaje y saco de arena

Figura 10.9 Plano y saco de arena

Un avión ligero de masa 1000 kg realiza un aterrizaje de emergencia en una pista corta. Con el motor apagado, aterriza en la pista a una velocidad de\(40 \mathrm{m} \cdot \mathrm{s}^{-1}\) Un gancho en el avión engancha un cable sujeto a un saco de arena de 120 kg y arrastra el saco de arena a lo largo. Si el coeficiente de fricción entre el saco de arena y la pista es\(\mu_{k}=0.4\), y si los frenos del avión dan una fuerza de retardo adicional de magnitud 1400 N, ¿hasta dónde llega el avión antes de que se detenga?

Solución: Supondremos que cuando el avión enganche el saco de arena, la colisión es instantánea por lo que el impulso en la dirección horizontal permanece constante,

\[p_{x, i}=p_{x, 1} \nonumber \]

Entonces conocemos la velocidad del avión y el saco de arena inmediatamente después de la colisión. Después de la colisión, hay dos fuerzas externas que actúan sobre el sistema del avión y saco de arena, la fricción entre el saco de arena y el suelo y la fuerza de frenado de la pista en el avión. Entonces podemos usar la Segunda Ley de Newton para determinar la aceleración y luego la cinemática unidimensional para encontrar la distancia recorrida por el avión ya que podemos determinar el cambio en la energía cinética.

El impulso del avión inmediatamente antes de la colisión es

\[\overrightarrow{\mathbf{p}}_{i}=m_{p} v_{p, i} \hat{\mathbf{i}} \nonumber \]

El impulso del avión y el saco de arena inmediatamente después de la colisión es

\[\overrightarrow{\mathbf{p}}_{1}=\left(m_{p}+m_{s}\right) v_{p, 1} \hat{\mathbf{i}} \nonumber \]

Debido a que el componente x del impulso es constante, podemos sustituir las Ecuaciones (10.9.16) y (10.9.17) en la Ecuación (10.9.15) rindiendo

\[m_{p} v_{p, i}=\left(m_{p}+m_{s}\right) v_{p, 1} \nonumber \]

La velocidad del avión y el saco de arena inmediatamente después de la colisión es

\[v_{p, 1}=\frac{m_{p} v_{p, i}}{m_{p}+m_{s}} \nonumber \]

Las fuerzas que actúan sobre el sistema que consiste en el plano y el saco de arena son la fuerza normal sobre el saco de arena,

\[\overrightarrow{\mathbf{N}}_{g, s}=N_{g, s} \hat{\mathbf{j}} \nonumber \]

la fuerza de fricción entre el saco de arena y el suelo

\[\overrightarrow{\mathbf{f}}_{k}=-f_{k} \hat{\mathbf{i}}=-\mu_{k} N_{g, s} \hat{\mathbf{i}}, \nonumber \]

la fuerza de frenado en el avión

\[\overrightarrow{\mathbf{F}}_{g, p}=-F_{g, p} \hat{\mathbf{i}} \nonumber \]

y la fuerza gravitacional sobre el sistema,

\[\left(m_{p}+m_{s}\right) \overrightarrow{\mathbf{g}}=-\left(m_{p}+m_{s}\right) g \hat{\mathbf{j}} \nonumber \]

La Segunda Ley de Newton en la\(\hat{\mathbf{i}}\) -dirección se convierte

\[-F_{g, p}-f_{k}=\left(m_{p}+m_{s}\right) a_{x} \nonumber \]

Si solo miramos las fuerzas verticales en el saco de arena, entonces la Segunda Ley de Newton en la\(\hat{\mathbf{j}}\) dirección se convierte

\[N-m_{s} g=0 \nonumber \]

La fuerza de fricción en el saco de arena es entonces

\[\overrightarrow{\mathbf{f}}_{k}=-\mu_{k} N_{g, s} \hat{\mathbf{i}}=-\mu_{k} m_{s} g \hat{\mathbf{i}} \nonumber \]

La Segunda Ley de Newton en la\(\hat{\mathbf{1}}\) -dirección se convierte

\[-F_{g, p}-\mu_{k} m_{s} g=\left(m_{p}+m_{s}\right) a_{x} \nonumber \]

El componente x de la aceleración del avión y la bolsa de arena es entonces

\[a_{x}=\frac{-F_{g, p}-\mu_{k} m_{s} g}{m_{p}+m_{s}} \nonumber \]

Elegimos nuestro origen en la ubicación del avión inmediatamente después de la colisión,\(x_{p}(0)=0\). Establecer t = 0 inmediatamente después de la colisión. El componente x de la velocidad del avión inmediatamente después de la colisión es\(v_{x, 0}=v_{p, 1}\). Establecer\(t=t_{f}\) cuando el avión acaba de llegar a una parada. Debido a que la aceleración es constante, las ecuaciones cinemáticas para el cambio de velocidad son

\[v_{x, f}\left(t_{f}\right)-v_{p, 1}=a_{x} t_{f} \nonumber \]

Podemos resolver esta ecuación para\(t=t_{f}\), donde\(v_{x, f}\left(t_{f}\right)=0\)

\[t_{f}=-v_{p, 1} / a_{x} t \nonumber \]

Entonces la posición del avión a la hora de descansar por primera vez es

\[x_{p}\left(t_{f}\right)-x_{p}(0)=v_{p, 1} t_{f}+\frac{1}{2} a_{x} t_{f}^{2}=-\frac{1}{2} \frac{v_{p, 1}^{2}}{a_{x}} \nonumber \]

Luego, usando\(x_{p}(0)=0\) y sustituyendo la Ecuación (10.9.26) en Ecuación (10.9.27) rinde

\[x_{p}\left(t_{f}\right)=\frac{1}{2} \frac{\left(m_{p}+m_{s}\right) v_{p, 1}^{2}}{\left(F_{g, p}+\mu_{k} m_{s} g\right)} \nonumber \]

Ahora usamos la condición de conservación de la ley de impulso durante la colisión, Ecuación (10.9.19) en la Ecuación (10.9.28) rindiendo

\[x_{p}\left(t_{f}\right)=\frac{m_{p}^{2} v_{p, i}^{2}}{2\left(m_{p}+m_{s}\right)\left(F_{g, p}+\mu_{k} m_{s} g\right)} \nonumber \]

Sustituir los valores dados en la Ecuación (10.9.28) rinde

\[x_{p}\left(t_{f}\right)=\frac{(1000 \mathrm{kg})^{2}\left(40 \mathrm{m} \cdot \mathrm{s}^{-1}\right)^{2}}{2(1000 \mathrm{kg}+120 \mathrm{kg})\left(1400 \mathrm{N}+(0.4)(120 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)\right)}=3.8 \times 10^{2} \mathrm{m} \nonumber \]