12.2: Ejemplos trabajados

Ejemplo\(\PageIndex{1}\): Filling a Coal Car

Un vagón vacío de carbón\(m_{0}\) de masa parte del reposo bajo una fuerza aplicada de magnitud F. Al mismo tiempo, el carbón comienza a correr hacia el automóvil a un ritmo constante b desde una tolva de carbón en reposo a lo largo de la vía (Figura 12.5). Encuentra la velocidad cuando se ha transferido una masa\(m_{c}\) de carbón.

Figura 12.5 Llenar un carro de carbón

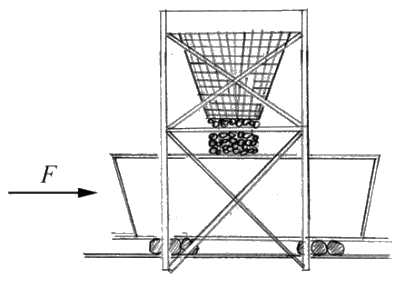
Solución

Analizaremos los cambios de impulso en la dirección horizontal, a la que llamamos la dirección x. Debido a que el carbón que cae no tiene ninguna velocidad horizontal, el carbón que cae no está transfiriendo ningún impulso en la dirección x al carro de carbón. Entonces tomaremos como nuestro sistema el vagón vacío de carbón y una masa\(m_{c}\) de carbón que ha sido transferida. Nuestro estado inicial en t = 0 es cuando el carro de carbón está vacío y en reposo antes de que se haya transferido cualquier carbón. El componente x del impulso de este estado inicial es cero,

\[p_{x}(0)=0 \nonumber \]

Nuestro estado final en\(t=t_{f}\) es cuando todo el carbón de masa\(m_{c}=b t_{f}\) ha sido transferido al automóvil que ahora se mueve a gran velocidad\(v_{f}\). El componente x del impulso de este estado final es

\[p_{x}\left(t_{f}\right)=\left(m_{0}+m_{c}\right) v_{f}=\left(m_{0}+b t_{f}\right) v_{f} \nonumber \]

Hay una fuerza externa constante\(F_{x}=F\) aplicada a través de la transferencia. El principio de impulso aplicado a la dirección x es

\[\int_{0}^{t_{f}} F_{x} d t=\Delta p_{x}=p_{x}\left(t_{f}\right)-p_{x}(0) \nonumber \]

Debido a que la fuerza es constante, la integral es simple y el principio de impulso se vuelve

\[F t_{f}=\left(m_{0}+b t_{f}\right) v_{f} \nonumber \]

Así que la velocidad final es

\[v_{f}=\frac{F t_{f}}{\left(m_{0}+b t_{f}\right)} \nonumber \]

Ejemplo\(\PageIndex{2}\): Emptying a Freight Car

Un vagón de carga de masa\(m_{c}\) contiene arena de masa\(m_{s}\). A\(t=0\) una fuerza horizontal constante de magnitud F se aplica en la dirección de laminación y al mismo tiempo se abre un puerto en el fondo para permitir que la arena fluya hacia fuera a la velocidad constante\(b=d m_{s} / d t\). Encuentra la velocidad del vagón de carga cuando se haya ido toda la arena (Figura 12.6). Supongamos que el vagón de carga está en reposo en\(t=0\).

Figura 12.6 Vaciado de un vagón de carga

Solución

Elija la dirección x positiva para apuntar en la dirección en la que se mueve el automóvil. Elige para el sistema la cantidad de arena en el carro susto en el tiempo t,\(m_{c}(t)\). En el tiempo t, el carro se mueve con velocidad\(\overrightarrow{\mathbf{v}}_{c}(t)=v_{c}(t) \hat{\mathbf{i}}\). El diagrama de impulso para el sistema en el tiempo t se muestra en el diagrama de la izquierda en la Figura 12.7.

Figura 12.7 Diagrama de impulso en el tiempo t y en el tiempo\(t+\Delta t\)

El impulso del sistema en el tiempo t viene dado por

\[\overrightarrow{\mathbf{p}}_{s y s}(t)=m_{c}(t) \overrightarrow{\mathbf{v}}_{c}(t) \nonumber \]

Durante el intervalo de tiempo\([t, t+\Delta t]\), una cantidad de arena de masa\(\Delta m_{s}\) sale del vagón de carga y la masa del vagón de carga cambia por\(m_{c}(t+\Delta t)=m_{c}(t)+\Delta m_{c}\), donde\(\Delta m_{c}=-\Delta m_{s}\). Al final del intervalo el carro se mueve con velocidad\(\overrightarrow{\mathbf{v}}_{c}(t+\Delta t)=\overrightarrow{\mathbf{v}}_{c}(t)+\Delta \overrightarrow{\mathbf{v}}_{c}=\left(v_{c}(t)+\Delta v_{c}\right) \hat{\mathbf{i}}\). El diagrama de momento para el sistema en el momento\(t+\Delta t\) se muestra en el diagrama de la derecha en la Figura 12.7. El impulso del sistema en el momento\(t+\Delta t\) viene dado por

\[\overrightarrow{\mathbf{p}}_{s y s}(t+\Delta t)=\left(\Delta m_{s}+m_{c}(t)+\Delta m_{c}\right)\left(\overrightarrow{\mathbf{v}}_{c}(t)+\Delta \overrightarrow{\mathbf{v}}_{c}\right)=m_{c}(t)\left(\overrightarrow{\mathbf{v}}_{c}(t)+\Delta \overrightarrow{\mathbf{v}}_{c}\right) \nonumber \]

Tenga en cuenta que la arena que sale del carro se muestra con velocidad\(\overrightarrow{\mathbf{v}}_{c}(t)+\Delta \overrightarrow{\mathbf{v}}_{c}\). Esto implica que toda la arena sale del carro con la velocidad del carro al final del intervalo. Esto es una aproximación. Debido a que la arena sale continua, la velocidad variará de\(\overrightarrow{\mathbf{v}}_{c}(t)\) a\(\overrightarrow{\mathbf{v}}_{c}(t)+\Delta \overrightarrow{\mathbf{v}}_{c}\) pero también lo hace el cambio de masa del automóvil y estas dos contribuciones al momento del sistema cancelan exactamente. El cambio en el impulso del sistema es entonces

\[\Delta \overrightarrow{\mathbf{p}}_{s y s}=\overrightarrow{\mathbf{p}}_{s y s}(t+\Delta t)-\overrightarrow{\mathbf{p}}_{s y s}(t)=m_{c}(t)\left(\overrightarrow{\mathbf{v}}_{c}(t)+\Delta \overrightarrow{\mathbf{v}}_{c}\right)-m_{c}(t) \overrightarrow{\mathbf{v}}_{c}(t)=m_{c}(t) \Delta \overrightarrow{\mathbf{v}}_{c} \nonumber \]

A lo largo del intervalo\(\overrightarrow{\mathbf{F}}=F \hat{\mathbf{i}}\) se aplica una fuerza constante al sistema por lo que el principio de impulso se convierte en

\[\overrightarrow{\mathbf{F}}=\lim _{\Delta t \rightarrow 0} \frac{\overrightarrow{\mathbf{p}}_{s y s}(t+\Delta t)-\overrightarrow{\mathbf{p}}_{s y s}(t)}{\Delta t}=\lim _{\Delta t \rightarrow 0} m_{c}(t) \frac{\Delta \overrightarrow{\mathbf{v}}_{c}}{\Delta t}=m_{c}(t) \frac{d \overrightarrow{\mathbf{v}}_{c}}{d t} \nonumber \]

Debido a que el movimiento es unidimensional, la Ecuación (12.3.9) escrita en términos de componentes x se convierte en

\[F=m_{c}(t) \frac{d v_{c}}{d t} \nonumber \]

Denotar por masa inicial del carro por\(m_{c, 0}=m_{c}+m_{s}\) donde\(m_{c}\) esta la masa del carro y\(m_{s}\) es la masa de la arena en el carro en\(t=0\). La masa de la arena que ha dejado el carro en el momento t viene dada por

\[m_{s}(t)=\int_{0}^{t} \frac{d m_{s}}{d t} d t=\int_{0}^{t} b d t=b t \nonumber \]

Así

\[m_{c}(t)=m_{c, 0}-b t=m_{c}+m_{s}-b t \nonumber \]

Por lo tanto, la ecuación (12.3.10) se convierte

\[F=\left(m_{c}+m_{s}-b t\right) \frac{d v_{c}}{d t} \nonumber \]

Esta ecuación se puede resolver para el componente x de la velocidad en el tiempo t,\(v_{c}(t)\) (que en este caso es la velocidad) por el método de separación de variables. Reescribir la ecuación (12.3.13) como

\[d v_{c}=\frac{F d t}{\left(m_{c}+m_{s}-b t\right)} \nonumber \]

Luego integre ambos lados de la Ecuación (12.3.14) con los límites como se muestra

\[\int_{v^{\prime}=0}^{v^{\prime}=v_{c}(t)} d v_{c}^{\prime}=\int_{t^{\prime}=0}^{t^{\prime}=t} \frac{F d t^{\prime}}{m_{c}+m_{s}-b t^{\prime}} \nonumber \]

La integración produce la velocidad del automóvil en función del tiempo

\[v_{c}(t)=-\left.\frac{F}{b} \ln \left(m_{c}+m_{s}-b t^{\prime}\right)\right|_{t=0} ^{\prime^{\prime}=t}=-\frac{F}{b} \ln \left(\frac{m_{c}+m_{s}-b t}{m_{c}+m_{s}}\right)=\frac{F}{b} \ln \left(\frac{m_{c}+m_{s}}{m_{c}+m_{s}-b t}\right) \nonumber \]

Al escribir la Ecuación (12.3.16), se utilizó la propiedad que\(\ln (a)-\ln (b)=\ln (a / b)\) y por lo tanto\(\ln (a / b)=-\ln (b / a)\). Tenga en cuenta que\(m_{c}+m_{s} \geq m_{c}+m_{s}-b t\), por lo que el término\(\ln \left(\frac{m_{c}+m_{s}}{m_{c}+m_{s}-b t}\right) \geq 0\), y la velocidad del automóvil aumenta como esperamos.

Ejemplo\(\PageIndex{3}\): Filling a Freight Car

El grano es soplado en el automóvil A desde el auto B a razón de b kilogramos por segundo. El grano sale de la tolva verticalmente hacia abajo, de manera que tiene la misma velocidad horizontal, u que el carro B, (Figura 12.8). El auto A está inicialmente en reposo antes de que se transfiera cualquier grano y tenga masa\(m_{A, 0}\). Al momento de interés, el auto A tiene masa\(m_{A}\) y velocidad v. Determinar una expresión para el vagón de velocidad A en función del tiempo t.

Figura 12.8 Llenado de un vagón de carga

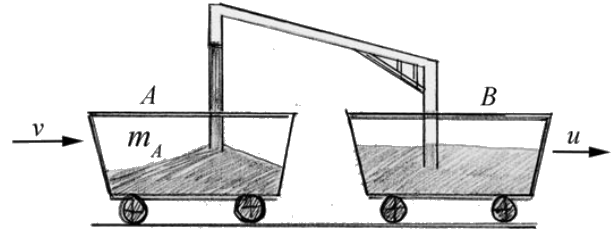
Solución

Elija la dirección x positiva hacia la derecha en la dirección en la que se mueven los autos. Definir el sistema en el tiempo t para que sea el carro y grano que ya está en él, que en conjunto tiene masa\(m_{A}(t)\) y la pequeña cantidad de material de masa\(\Delta m_{g}\) que se sopla en el carro A durante el intervalo de tiempo\([t, t+\Delta t]\) En el tiempo que se está moviendo con x -componente de la velocidad\(\mathcal{V}_{A}\). En el tiempo t, el carro A se mueve con velocidad\(\overrightarrow{\mathbf{v}}_{A}(t)=v_{A}(t) \hat{\mathbf{i}}\) y el material soplado en el carro se mueve con velocidad\(\overrightarrow{\mathbf{u}}=u \hat{\mathbf{i}}\) En el momento en que el\(t+\Delta t\) carro A se mueve con velocidad\(\overrightarrow{\mathbf{v}}_{A}(t)+\Delta \overrightarrow{\mathbf{v}}_{A}=\left(v_{A}(t)+\Delta v_{A}\right) \hat{\mathbf{i}}\), y la masa del carro A es\(m_{A}(t+\Delta t)=m_{A}(t)+\Delta m_{A}\) donde\(\Delta m_{A}=\Delta m_{g}\). El diagrama de impulso para los tiempos t y para\(t+\Delta t\) se muestra en la Figura 12.9.

Figura 12.9 Diagrama de impulso en los tiempos t y\(t+\Delta t\)

El impulso en el tiempo t es

\[\overrightarrow{\mathbf{P}}_{s y s}(t)=m_{A}(t) \overrightarrow{\mathbf{v}}_{A}(t)+\Delta m_{g} \overrightarrow{\mathbf{u}} \nonumber \]

El impulso en el momento\(t+\Delta t\) es

\[\overrightarrow{\mathbf{P}}_{s y s}(t+\Delta t)=\left(m_{A}(t)+\Delta m_{A}\right)\left(\overrightarrow{\mathbf{v}}_{A}(t)+\Delta \overrightarrow{\mathbf{v}}_{A}\right) \nonumber \]

No hay fuerzas externas que actúen sobre el sistema en la dirección x y las fuerzas externas que actúan sobre el sistema perpendiculares a la suma de movimiento a cero, por lo que el principio de impulso se convierte en

\[\overrightarrow{\mathbf{0}}=\lim _{\Delta t \rightarrow 0} \frac{\overrightarrow{\mathbf{P}}_{s y s}(t+\Delta t)-\overrightarrow{\mathbf{P}}_{s y s}(t)}{\Delta t} \nonumber \]

Usando los resultados anteriores (Ecuaciones (12.3.17) y (12.3.18), el principio de impulso se convierte en

\[\overrightarrow{\mathbf{0}}=\lim _{\Delta t \rightarrow 0} \frac{\left(m_{A}(t)+\Delta m_{A}\right)\left(\overrightarrow{\mathbf{v}}_{A}(t)+\Delta \overrightarrow{\mathbf{v}}_{A}\right)-\left(m_{A}(t) \overrightarrow{\mathbf{v}}_{A}(t)+\Delta m_{g} \overrightarrow{\mathbf{u}}\right)}{\Delta t} \nonumber \]

que después de usar la condición que\(\Delta m_{A}=\Delta m_{g}\) y algún reordenamiento se convierte

\[\overrightarrow{\mathbf{0}}=\lim _{\Delta t \rightarrow 0} \frac{m_{A}(t) \Delta \overrightarrow{\mathbf{v}}_{A}}{\Delta t}+\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{A}\left(\overrightarrow{\mathbf{v}}_{A}(t)-\overrightarrow{\mathbf{u}}\right)}{\Delta t}+\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{A} \Delta \overrightarrow{\mathbf{v}}_{A}}{\Delta t} \nonumber \]

En el límite as, el producto\(\Delta m_{A} \Delta \overrightarrow{\mathbf{V}}_{A}\) es un diferencial de segundo orden (el producto de dos diferenciales de primer orden) y el término\(\Delta m_{A} \Delta \overrightarrow{\mathbf{v}}_{A} / \Delta t\) se aproxima a cero, por lo tanto el principio de impulso arroja la ecuación diferencial

\[\overrightarrow{\mathbf{0}}=m_{A}(t) \frac{d \overrightarrow{\mathbf{v}}_{A}}{d t}+\frac{d m_{A}}{d t}\left(\overrightarrow{\mathbf{v}}_{A}(t)-\overrightarrow{\mathbf{u}}\right) \nonumber \]

El componente x de la Ecuación (12.3.22) es entonces

\[0=m_{A}(t) \frac{d v_{A}}{d t}+\frac{d m_{A}}{d t}\left(v_{A}(t)-u\right) \nonumber \]

Reordenando términos y utilizando el hecho de que el material es soplado en el automóvil A a una velocidad constante\(b \equiv d m_{A} / d t\), tenemos que la tasa de cambio del componente x de la velocidad del automóvil A viene dada por

\[\frac{d v_{A}(t)}{d t}=\frac{b\left(u-v_{A}(t)\right)}{m_{A}(t)} \nonumber \]

No podemos integrar directamente la Ecuación (12.3.24) con respecto a dt porque la masa del automóvil A es función del tiempo. Para encontrar el componente x de la velocidad del automóvil A necesitamos conocer la relación entre la masa del automóvil A y el componente x de la velocidad del automóvil A. Hay dos enfoques. En el primer enfoque separamos las variables en la Ecuación (12.3.24) donde hemos suprimido la dependencia de t en las expresiones para\(m_{A}\) y\(\mathcal{V}_{A}\) rendimiento

\[\frac{d v_{A}}{u-v_{A}}=\frac{d m_{A}}{m_{A}} \nonumber \]

que se convierte en la ecuación integral

\[\int_{v_{A}^{\prime}=0}^{v_{A}^{\prime}=v_{A}(t)} \frac{d v_{A}^{\prime}}{u-v_{A}^{\prime}}=\int_{m_{A}^{\prime}=m_{A, 0}}^{m_{A^{\prime}}^{\prime}=m_{A}(t)} \frac{d m_{A}^{\prime}}{m_{A}^{\prime}} \nonumber \]

donde\(m_{A, 0}\) es la masa del carro antes de que cualquier material haya sido soplado. Después de la integración tenemos eso

\[\ln \frac{u}{u-v_{A}(t)}=\ln \frac{m_{A}(t)}{m_{A, 0}} \nonumber \]

Exponenciar los rendimientos de ambos lados

\[\frac{u}{u-v_{A}(t)}=\frac{m_{A}(t)}{m_{A, 0}} \nonumber \]

Podemos resolver esta ecuación para el componente x de la velocidad del automóvil

\[v_{A}(t)=\frac{m_{A}(t)-m_{A, 0}}{m_{A}(t)} u \nonumber \]

Debido a que el material se sopla en el automóvil a una velocidad constante\(b \equiv d m_{A} / d t\), la masa del automóvil en función del tiempo viene dada por

\[m_{A}(t)=m_{A, 0}+b t \nonumber \]

Por lo tanto, al sustituir la Ecuación (12.3.30) en la Ecuación (12.3.29) se obtiene el componente x de la velocidad del automóvil en función del tiempo

\[v_{A}(t)=\frac{b t}{m_{A, 0}+b t} u \nonumber \]

En un segundo enfoque, sustituimos la Ecuación (12.3.30) por la Ecuación (12.3.24) rindiendo

\[\frac{d v_{A}}{d t}=\frac{b\left(u-v_{A}\right)}{m_{A, 0}+b t} \nonumber \]

Variables separadas en la Ecuación (12.3.32):

\[\frac{d v_{A}}{u-v_{A}}=\frac{b d t}{m_{A, 0}+b t} \nonumber \]

que luego se convierte en la ecuación integral

\[\int_{v_{A}^{\prime}=0}^{v_{A}^{\prime}=v_{A}(t)} \frac{d v_{A}^{\prime}}{u-v_{A}^{\prime}}=\int_{t^{\prime}=0}^{t^{\prime}=t^{\prime}} \frac{d t^{\prime}}{m_{A, 0}+b t^{\prime}} \nonumber \]

Rendimientos de integración

\[\ln \frac{u}{u-v_{A}(t)}=\ln \frac{m_{A, 0}+b t}{m_{A, 0}} \nonumber \]

Nuevamente exponenciar ambos lados dando como resultado

\[\frac{u}{u-v_{A}(t)}=\frac{m_{A, 0}+b t}{m_{A, 0}} \nonumber \]

Después de alguna manipulación algebraica podemos encontrar la velocidad del auto en función del tiempo

\[v_{A}(t)=\frac{b t}{m_{A, 0}+b t} u \nonumber \]

de acuerdo con la Ecuación (12.3.31).

Resultado de la comprobación:

Podemos reescribir la Ecuación (12.3.37) como

\[\left(m_{A, 0}+b t\right) v_{A}(t)=b t u \nonumber \]

que ilustra el punto en que el impulso del sistema en el tiempo t es igual al impulso del grano que ha sido transferido al sistema durante el intervalo [0, t].

Ejemplo\(\PageIndex{4}\): Boat and Fire Hose

Un bote ardiente de masa\(m_{0}\) está inicialmente en reposo. Un bomberos se para en un puente y rocía agua sobre el bote. El agua sale de la manguera contra incendios con una velocidad u a una tasa α (medida en\(\mathrm{kg} \cdot \mathrm{s}^{-1}\)). Supongamos que el movimiento de la embarcación y el chorro de agua son horizontales, que la gravedad no juega ningún papel, y que el río puede ser tratado como una superficie sin fricción. También supongamos que el cambio en la masa de la embarcación se debe únicamente al chorro de agua y que toda el agua del chorro se agrega a la embarcación, (Figura 12.10).

Figura 12.10 Ejemplo 12.4

1. En un intervalo de tiempo\([t, t+\Delta t]\), una cantidad de agua\(\Delta m\) golpea el bote. Elija un sistema. ¿El impulso total es constante en su sistema? Escribe una ecuación diferencial que resulte del análisis de los cambios de impulso dentro de tu sistema.
2. Integra la ecuación diferencial que encontraste en la parte a), para encontrar la velocidad v (m) en función de la masa creciente m de la embarcación,\(m_{0}\), y u.

Solución

Tomemos como nuestro sistema la embarcación, la cantidad de agua de masa\(\Delta m_{w}\) que ingresa a la embarcación durante el intervalo de tiempo\([t, t+\Delta t]\) y cualquier agua que esté en la embarcación en el tiempo t. El agua de la manguera contra incendios tiene una velocidad u. Denotar la masa de la embarcación (incluyendo algo de agua) en el tiempo t by\(m_{b} \equiv m_{b}(t)\), y la velocidad de la embarcación por\(v \equiv v_{b}(t)\). En\(t+\Delta t\) el momento la velocidad de la embarcación es\(v+\Delta v\). Elija la dirección x positiva en la dirección en la que se mueve la embarcación. Después los x -componentes del momento del sistema en el tiempo t y se\(t+\Delta t\) muestran en la Figura 12.11.

Figura 12.11 Diagramas de momento para barco en llamas

Debido a que estamos asumiendo que la embarcación en llamas se desliza con una resistencia insignificante y que la gravedad tiene un efecto despreciable en el arco del chorro de agua, no hay fuerzas externas que actúen sobre el sistema en la dirección x. Por lo tanto, el componente x del momento del sistema es constante durante el intervalo\([t, t+\Delta t]\) y así

\[0=\lim _{\Delta t \rightarrow 0} \frac{p_{x}(t+\Delta t)-p_{x}(t)}{\Delta t} \nonumber \]

Usando la información de la figura anterior, la Ecuación (12.3.39) se convierte

\[0=\lim _{\Delta t \rightarrow 0} \frac{\left(m_{b}+\Delta m_{w}\right)(v+\Delta v)-\left(\Delta m_{w} u+m_{b} v\right)}{\Delta t} \nonumber \]

La ecuación (12.3.40) simplifica a

\[0=\lim _{\Delta t \rightarrow 0} m_{b} \frac{\Delta v}{\Delta t}+\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w}}{\Delta t} v+\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w} \Delta v}{\Delta t}-\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w}}{\Delta t} u \nonumber \]

El tercer término se desvanece cuando tomamos el límite\(\Delta t \rightarrow 0\) porque es de segundo orden en las cantidades infinitesimales (en este caso\(\Delta m_{w} \Delta v\)) y al dividirlo así por\(\Delta t\) la cantidad es de primer orden y por lo tanto desaparece ya que ambos\(\Delta m_{w} \rightarrow 0\) y la\(\Delta v \rightarrow 0\) Ecuación (12.3.41) se convierte

\[0=\lim _{\Delta t \rightarrow 0} m_{b} \frac{\Delta v}{\Delta t}+\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w}}{\Delta t} v-\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w}}{\Delta t} u \nonumber \]

Ahora usamos la definición de los derivados:

\[\lim _{\Delta t \rightarrow 0} \frac{\Delta v}{\Delta t}=\frac{d v}{d t} ; \lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w}}{\Delta t}=\frac{d m_{w}}{d t} \nonumber \]

en la Ecuación (12.3.42) para financiar la ecuación diferencial que describe la relación entre la aceleración de la embarcación y la tasa de cambio de tiempo de la masa de agua que ingresa a la embarcación

\[0=m_{b} \frac{d v}{d t}+\frac{d m_{w}}{d t}(v-u) \nonumber \]

La masa de la embarcación va en aumento debido a la adición del agua. Dejar\(m_{w}(t)\) denotar la masa del agua que está en el bote en el tiempo t .Entonces la masa de la embarcación se puede escribir como

\[m_{b}(t)=m_{0}+m_{w}(t) \nonumber \]

donde\(m_{0}\) se encuentra la masa de la embarcación antes de que entre agua alguna. Tenga en cuenta que estamos descuidando el efecto del fuego en la masa de la embarcación. Ecuación Diferenciante (12.3.45) con respecto a rendimientos de tiempo

\[\frac{d m_{b}}{d t}=\frac{d m_{w}}{d t} \nonumber \]

Entonces la Ecuación (12.3.44) se convierte

\[0=m_{b} \frac{d v}{d t}+\frac{d m_{b}}{d t}(v-u) \nonumber \]

(b) Podemos integrar esta ecuación a través de la técnica de separación de variables. Reescribir la ecuación (12.3.47) como (cancelar el factor común dt)

\[\frac{d v}{v-u}=-\frac{d m_{b}}{m_{b}} \nonumber \]

Entonces podemos integrar ambos lados de la Ecuación (12.3.48) con los límites como se muestra

\[\int_{v=0}^{v(t)} \frac{d v}{v-u}=-\int_{m_{0}}^{m_{b}(t)} \frac{d m_{b}}{m_{b}} \nonumber \]

Rendimientos de integración

\[\ln \left(\frac{v(t)-u}{-u}\right)=-\ln \left(\frac{m_{b}(t)}{m_{0}}\right) \nonumber \]

Recordemos que\(\ln (a / b)=-\ln (b / a)\) así la Ecuación (12.3.50) se convierte

\[\ln \left(\frac{v(t)-u}{-u}\right)=\ln \left(\frac{m_{0}}{m_{b}(t)}\right) \nonumber \]

Recordemos también que\(\exp (\ln (a / b))=a / b\) y así exponenciando ambos lados de la Ecuación (12.3.51) rinde

\[\frac{v(t)-u}{-u}=\frac{m_{0}}{m_{b}(t)} \nonumber \]

Entonces la velocidad de la embarcación en el tiempo t se puede expresar como

\[v(t)=u\left(1-\frac{m_{0}}{m_{b}(t)}\right) \nonumber \]

Resultado de la comprobación:

Podemos reescribir la Ecuación (12.3.52) como

\[m_{b}(t)(v(t)-u)=-m_{0} u \Rightarrow m_{b}(t) v(t)=\left(m_{b}(t)-m_{0}\right) u \nonumber \]

Recordemos que la masa del agua que ingresa al carro durante el intervalo [0, t] es\(m_{w}(t)=m_{b}(t)-m_{0}\). Por lo tanto, la ecuación (12.3.54) se convierte

\[m_{b}(t) v(t)=m_{w}(t) u \nonumber \]

Durante la interacción entre el chorro de agua y la embarcación, el agua transfiere una cantidad de impulso\(m_{w}(t) u\) a la embarcación y al automóvil produciendo un impulso\(m_{b}(t) v(t)\). Debido a que toda el agua que choca con la embarcación termina en la embarcación, todas las fuerzas de interacción entre el chorro de agua y la embarcación son fuerzas internas. El bote retrocede hacia adelante y el agua retrocede y a través de colisiones con el barco se queda en el bote. Por lo tanto, si elegimos como nuestro sistema, toda el agua que finalmente termina en la embarcación y en la embarcación entonces el principio de impulso establece

\[p_{s y s}(t)=p_{s y s}(0) \nonumber \]

donde\(p_{s y s}(0)=m_{w}(t) u\) está el impulso de toda el agua que finalmente termina en el bote.

Tenga en cuenta que el problema no pidió encontrar la velocidad de la embarcación como una función t. Ahora vamos a mostrar cómo encontrar eso. Comenzamos observando que

\[\frac{d m_{b}}{d t}=\frac{d m_{w}}{d t} \neq \alpha \nonumber \]

donde la constante\(\alpha\) se mide en\(\mathrm{kg} \cdot \mathrm{s}^{-1}\) y se especifica como una constante dada de acuerdo con la información en la declaración del problema. El motivo es que\(\alpha\) es la tasa que el agua es expulsada de la manguera pero no la tasa que el agua ingresa a la embarcación.

Figura 12.12 Masa por unidad de longitud del chorro de agua

Considera una pequeña cantidad de agua que se mueve con velocidad u que, en un intervalo de tiempo Δt, fluye a través de un área de sección transversal orientada perpendicular al flujo (ver Figura 12.12). El área es mayor que el área de la sección transversal del chorro de agua. La cantidad de agua que fluye a través del elemento de área\(\Delta m=\lambda u \Delta t\) donde λ es la masa por unidad de longitud del chorro y\(u \Delta t\) es la longitud del chorro que fluye a través del área en el intervalo Δt. La tasa de masa de agua que fluye a través del elemento de área de sección transversal es entonces

\[\alpha=\frac{\Delta m}{\Delta t}=\lambda u \nonumber \]

En la Figura 12.13 consideramos una pequeña longitud\(u \Delta t\) del chorro de agua que se encuentra justo detrás de la embarcación en el tiempo t. Durante el intervalo de tiempo\([t, t+\Delta t]\), la embarcación se mueve una distancia\(v \Delta t\).

Figura 12.13 Cantidad de agua que ingresa a la embarcación en intervalo de tiempo\([t, t+\Delta t]\)

Solo una fracción de la longitud\(u \Delta t\) del agua ingresa a la embarcación y está dada por

\[\Delta m_{w}=\lambda(u-v) \Delta t=\frac{\alpha}{u}(u-v) \Delta t \nonumber \]

Dividiendo la Ecuación (12.3.59) a través de por\(\Delta t\) y tomando límites tenemos que

\[\frac{d m_{w}}{d t}=\lim _{\Delta t \rightarrow 0} \frac{\Delta m_{w}}{\Delta t}=\frac{\alpha}{u}(u-v)=\alpha\left(1-\frac{v}{u}\right) \nonumber \]

Sustituyendo la ecuación (12.3.53) y la ecuación (12.3.46) en la ecuación (12.3.60) rendimientos

\[\frac{d m_{b}}{d t}=\alpha\left(1-\frac{v}{u}\right)=\alpha \frac{m_{0}}{m_{b}(t)} \nonumber \]

Podemos integrar esta ecuación separando variables para encontrar una expresión integral para la masa de la embarcación en función del tiempo

\[\int_{m_{0}}^{m_{0}(t)} m_{b} d m_{b}=\alpha m_{0} \int_{t=0}^{t} d t \nonumber \]

Podemos integrar fácilmente ambos lados de la Ecuación (12.3.62) rindiendo

\[\frac{1}{2}\left(m_{b}(t)^{2}-m_{0}^{2}\right)=\alpha m_{b, 0} t \nonumber \]

La masa de la embarcación en función del tiempo es entonces

\[m_{b}(t)=m_{0} \sqrt{1+2 \frac{\alpha t}{m_{0}}} \nonumber \]

Ahora sustituimos la Ecuación (12.3.64) por la Ecuación (12.3.65) produciendo la velocidad del barco en llamas en función del tiempo

\[v(t)=u\left(1-\frac{1}{\sqrt{1+2 \frac{\alpha t}{m_{b, 0}}}}\right) \nonumber \]