13.5: Trabajo realizado por Fuerzas No Constantes

Considere un cuerpo que se mueve en la dirección x bajo la influencia de una fuerza no constante en la dirección x,\(\overrightarrow{\mathbf{F}}=F_{x} \hat{\mathbf{i}}\). El cuerpo se mueve de una posición inicial\(x_{i}\) a una posición final\(x_{f}\). Para calcular el trabajo realizado por una fuerza no constante, dividiremos el desplazamiento del punto de aplicación de la fuerza en un gran número N de pequeños desplazamientos\(\Delta x_{j}\) donde el índice j marca el\(j_{th}\) desplazamiento y toma valores enteros de 1 a N. Dejar\(\left(F_{x, j}\right)_{\text {ave }}\) denotar el valor promedio del componente x de la fuerza en el intervalo de desplazamiento\(\left[x_{j-1}, x_{j}\right]\). Para el intervalo de\(j_{th}\) desplazamiento calculamos la contribución al trabajo.

\[W_{j}=\left(F_{x, j}\right)_{\text {ave }} \Delta x_{j} \nonumber \]

Esta contribución es un escalar por lo que sumamos estas cantidades escalares para obtener el trabajo total

\[W_{N}=\sum_{j=1}^{j=N} W_{j}=\sum_{j=1}^{j=N}\left(F_{x, j}\right)_{\text {ave }} \Delta x_{j} \nonumber \]

La suma en la Ecuación (13.5.2) depende del número de divisiones N y del ancho de los intervalos\(\Delta x_{j}\). Para definir una cantidad que sea independiente de las divisiones, tomamos el límite como\(N \rightarrow \infty\) y\(\left|\Delta x_{j}\right| \rightarrow 0\) para todos j. El trabajo es entonces

\[W=\lim _{N \rightarrow \infty \atop\left|\Delta x_{j}\right| \rightarrow 0} \sum_{j=1}^{j=N}\left(F_{x, j}\right)_{\text {ave }} \Delta x_{j}=\int_{x=x_{i}}^{x=x_{f}} F_{x}(x) d x \nonumber \]

Esta última expresión es la integral definitiva del componente x de la fuerza con respecto al parámetro x. En la Figura 13.5 se grafica el componente x de la fuerza en función del parámetro x. La integral de trabajo es el área bajo esta curva entre\(x=x_{i}\) y\(x=x_{f}\).

Figura 13.5 Gráfica de x -componente de una fuerza\(F_{x}(x)\) de muestra en función de x.

Ejemplo\(\PageIndex{1}\): Work done by the Spring Force

Conecte un extremo de un resorte sin estirar de longitud\(l_{0}\) con la constante de resorte k a un objeto que descansa sobre una mesa lisa sin fricción y fije el otro extremo del resorte a una pared. Elija un origen como se muestra en la figura. Estire el resorte en una cantidad\(x_{i}\) y libere el objeto. ¿Cuánto trabajo hace el resorte en el objeto cuando el resorte se estira en una cantidad\(x_{f}\)?

Figura 13.6 Equilibrio, estados inicial y final para un resorte

Solución

Primero comenzamos eligiendo un sistema de coordenadas con nuestro origen ubicado en la posición del objeto cuando el resorte está sin estirar (o sin comprimir). Elegimos el vector\(\hat{\mathbf{i}}\) unitario para apuntar en la dirección en la que el objeto se mueve cuando se estira el resorte. Elegimos la función de coordenadas x para denotar la posición del objeto con respecto al origen. Mostramos la función de coordenadas y el diagrama de fuerza de cuerpo libre en la siguiente figura.

Figura 13.6a Fuerza de resorte

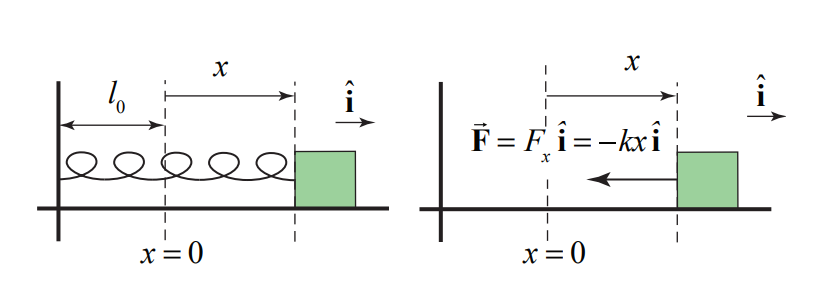
La fuerza del resorte sobre el objeto viene dada por (Figura 13.6a)

\[\overrightarrow{\mathbf{F}}=F_{x} \hat{\mathbf{i}}=-k x \hat{\mathbf{i}} \nonumber \]

En la Figura 13.7 se muestra la gráfica del componente x de la fuerza elástica\(F_{x}(x)\), en función de x

Figura 13.7 Gráfica de la fuerza del resorte\(F_{x}(x)\) frente al desplazamiento x

El trabajo realizado es sólo el área bajo la curva para el intervalo\(x_{i}\) a\(x_{f}\),

\[W=\int_{x^{\prime}=x_{i}}^{x^{\prime}=x_{f}} F_{x}\left(x^{\prime}\right) d x^{\prime}=\int_{x^{\prime}=x_{i}}^{x^{\prime}=x_{f}}-k x^{\prime} d x^{\prime}=-\frac{1}{2} k\left(x_{f}^{2}-x_{i}^{2}\right) \nonumber \]

Este resultado es independiente del signo de\(x_{i}\) y\(x_{f}\) porque ambas cantidades aparecen como cuadrados. Si el resorte está menos estirado o comprimido en el estado final que en el estado inicial, entonces el valor absoluto,\(\left|x_{f}\right|<\left|x_{i}\right|\) y el trabajo realizado por la fuerza del resorte es positivo. La fuerza del resorte realiza un trabajo positivo en el cuerpo cuando el resorte pasa de un estado de “mayor tensión” a un estado de “menor tensión”.