16.2: Rotación de Eje Fijo- Cinemática Rotacional

Rotación de Eje Fijo

Un ejemplo sencillo de rotación alrededor de un eje fijo es el movimiento de un disco compacto en un reproductor de CD, el cual es accionado por un motor dentro del reproductor. En un modelo simplificado de este movimiento, el motor produce aceleración angular, provocando que el disco gire. A medida que el disco se pone en movimiento, las fuerzas resistivas se oponen al movimiento hasta que el disco ya no tiene ninguna aceleración angular, y el disco ahora gira a una velocidad angular constante. A lo largo de este proceso, el CD gira alrededor de un eje que pasa por el centro del disco, y es perpendicular al plano del disco (ver Figura 16.1). Este tipo de movimiento se denomina rotación de eje fijo.

Figura 16.1 Rotación de un disco compacto alrededor de un eje fijo.

Cuando montamos una bicicleta hacia adelante, las ruedas giran alrededor de un eje que pasa por el centro de cada rueda y perpendicular al plano de la rueda (Figura 16.2). Mientras la bicicleta no gire, este eje sigue apuntando en la misma dirección. Este movimiento es más complicado que nuestro CD giratorio porque la rueda se mueve (traslada) con algún centro de velocidad de masa,\(\overrightarrow{\mathbf{v}}_{\mathrm{cm}}\) y girando con una velocidad angular\(\omega\).

Figura 16.2 Rotación de eje fijo y traslación del centro de masa para una rueda de bicicleta.

Cuando giramos el manillar de la bicicleta, cambiamos la trayectoria de la bicicleta y el eje de rotación de cada rueda cambia de dirección. Otros ejemplos de rotación de eje no fijo son el movimiento de una peonza, o un giroscopio, o incluso el cambio en la dirección del eje de rotación de la tierra. Este tipo de movimiento es mucho más difícil de analizar, por lo que nos limitaremos en este capítulo a considerar la rotación de eje fijo, con o sin traslación.

Velocidad angular y aceleración angular

Para un cuerpo rígido sometido a rotación de eje fijo, podemos dividir el cuerpo en elementos de pequeño volumen con masa\(\Delta m_{i}\). Cada uno de estos elementos de volumen se mueve en un círculo de radio\(r_{i}\) alrededor del eje de rotación (Figura 16.3).

Figura 16.3 Sistema de coordenadas para rotación de eje fijo.

Adoptaremos la notación implícita en la Figura 16.3, y denotaremos el vector desde el eje hasta el punto donde se ubica el elemento de masa como\(\overrightarrow{\mathbf{r}}_{i}\), con magnitud\(r_{i}=\left|\overrightarrow{\mathbf{r}}_{i}\right|\). Supongamos que el eje fijo de rotación es el eje z. Introducir un sistema de coordenadas diestro para un ángulo θ en el plano de rotación y la elección de la dirección z positiva perpendicular a ese plano de rotación. Recordemos nuestra definición del vector de velocidad angular. El vector de velocidad angular se dirige a lo largo del eje z con componente z igual a la derivada de tiempo del ángulo θ,

\[\overrightarrow{\boldsymbol{\omega}}=\frac{d \theta}{d t} \hat{\mathbf{k}}=\omega_{z} \hat{\mathbf{k}} \nonumber \]

El vector de velocidad angular para el elemento de masa sometido a rotación de eje fijo con\(\omega_{z}>0\) se muestra en la Figura 16.4. Debido a que el cuerpo es rígido, todos los elementos de masa tendrán la misma velocidad angular\(\overrightarrow{\boldsymbol{\omega}}\) y de ahí la misma aceleración angular\(\vec{\alpha}\). Si los cuerpos no tuvieran la misma velocidad angular, los elementos de masa “alcanzarían” o “pasarían” entre sí, impedidos por la suposición de cuerpo rígido.

Figura 16.4 Vector de velocidad angular para un elemento de masa para rotación de eje fijo

De manera similar, todos los puntos del cuerpo rígido tienen la misma aceleración angular,

\[\vec{\alpha}=\frac{d^{2} \theta}{d t^{2}} \hat{\mathbf{k}}=\alpha_{z} \hat{\mathbf{k}} \nonumber \]

El vector de aceleración angular se muestra en la Figura 16.5.

Figura 16.5 Vector de aceleración angular para un cuerpo rígido que gira alrededor del eje z

Convención de Signo: Velocidad Angular y Aceleración Angular

Para problemas rotacionales siempre elegiremos un sistema de coordenadas cilíndricas diestras. Si el eje z positivo apunta hacia arriba, entonces elegimos θ para estar aumentando en sentido contrario a las agujas del reloj como se muestra en las Figuras 16.4 y 16.5. Si el cuerpo rígido gira en sentido contrario a las agujas del reloj, entonces el componente z de la velocidad angular es positivo,\(\omega_{z}=d \theta / d t>0\). El vector de velocidad angular apunta entonces en la\(+\hat{\mathbf{k}}\) dirección -como se muestra en la Figura 16.4. Si el cuerpo rígido gira en el sentido de las agujas del reloj, entonces el componente z de la velocidad angular de la velocidad angular es negativo,\(\omega_{z}=d \theta / d t<0\). El vector de velocidad angular apunta entonces en la\(-\hat{\mathbf{k}}\) dirección -dirección.

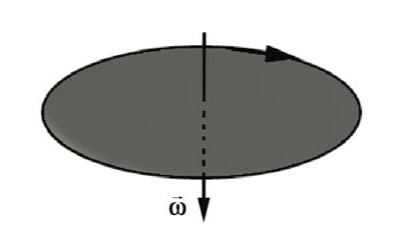
Si el cuerpo rígido aumenta su velocidad de rotación en sentido contrario a las agujas del reloj (positivo) entonces el componente z de la aceleración angular es positivo,\(\alpha_{z} \equiv d^{2} \theta / d t^{2}=d \omega_{z} / d t>0\). El vector de aceleración angular apunta entonces en la\(+\hat{\mathbf{k}}\) dirección -como se muestra en la Figura 16.5. Si el cuerpo rígido disminuye su velocidad de rotación en sentido contrario a las agujas del reloj (positivo) entonces el componente z de la aceleración angular es negativo,\(\alpha_{z}=d^{2} \theta / d t^{2}=d \omega_{z} / d t<0\) El vector de aceleración angular luego apunta en la\(-\hat{\mathbf{k}}\) dirección -dirección. Para enunciar esto de manera más general, si\(\vec{\alpha}\) y\(\overrightarrow{\boldsymbol{\omega}}\) apuntar en la misma dirección, el cuerpo está acelerando, si en direcciones opuestas, el cuerpo se está desacelerando. Este resultado general es independiente de la elección del sentido positivo de rotación. Obsérvese que en la Figura 16.1, el CD tiene los puntos del vector de velocidad angular hacia abajo (en la\(-\hat{\mathbf{k}}\) dirección -dirección.

Velocidad tangencial y aceleración tangencial

Debido a que el pequeño elemento de masa,\(\Delta m_{i}\) se mueve en un círculo de radio\(r_{i}\) con velocidad angular\(\overrightarrow{\boldsymbol{\omega}}=\omega_{z} \hat{\mathbf{k}}\), el elemento tiene un componente de velocidad tangencial

\[v_{\theta, i}=r_{i} \omega_{z} \nonumber \]

Si la magnitud de la velocidad tangencial está cambiando, el elemento de masa sufre una aceleración tangencial dada por

\[a_{\theta, i}=r_{i} \alpha_{z} \nonumber \]

Recordemos que el elemento de masa siempre está acelerando hacia adentro con componente radial dado por

\[a_{r, i}=-\frac{v_{\theta, i}^{2}}{r_{i}}=-r_{i} \omega_{z}^{2} \nonumber \]

Ejemplo\(\PageIndex{1}\)

Un plato giratorio es un disco uniforme de masa\(1.2\) kg y un radio\(1.3 \times 10^{1} \mathrm{cm}\). El plato giratorio gira inicialmente en sentido antihorario cuando se ve desde arriba a una velocidad constante de\(f_{0}=33 \text { cycles } \cdot \min ^{-1}\) (33 rpm). El motor se apaga y el plato giratorio se ralentiza hasta detenerse en 8.0 s. Supongamos que la aceleración angular es constante. (a) ¿Cuál es la velocidad angular inicial del plato giratorio? (b) ¿Cuál es la aceleración angular del plato giratorio?

Solución

(a) Elija un sistema de coordenadas que se muestra en la Figura 16.6.

Figura 16.6 Sistema de coordenadas para plataforma giratoria

Inicialmente, el disco está girando con una frecuencia

\[f_{0}=\left(33 \frac{\text { cycles }}{\min }\right)\left(\frac{1 \min }{60 \mathrm{s}}\right)=0.55 \mathrm{cycles} \cdot \mathrm{s}^{-1}=0.55 \mathrm{Hz} \nonumber \]

por lo que la velocidad angular inicial tiene magnitud

\[\omega_{0}=2 \pi f_{0}=\left(2 \pi \frac{\text { radian }}{\text { cycle }}\right)\left(0.55 \frac{\text { cycles }}{\mathrm{s}}\right)=3.5 \mathrm{rad} \cdot \mathrm{s}^{-1} \nonumber \]

El vector de velocidad angular apunta en la\(+\hat{\mathbf{k}}\) dirección -como se muestra arriba.

(b) La velocidad angular final es cero, por lo que el componente de la aceleración angular es

\[\alpha_{z}=\frac{\Delta \omega_{z}}{\Delta t}=\frac{\omega_{f}-\omega_{0}}{t_{f}-t_{0}}=\frac{-3.5 \mathrm{rad} \cdot \mathrm{s}^{-1}}{8.0 \mathrm{s}}=-4.3 \times 10^{-1} \mathrm{rad} \cdot \mathrm{s}^{-2} \nonumber \]

El componente z de la aceleración angular es negativo, el disco se está desacelerando y así el vector de aceleración angular luego apunta en la\(-\hat{\mathbf{k}}\) dirección -como se muestra en la Figura 16.7.

Figura 16.7 Vector de aceleración angular para plato giratorio